7.4 – Cinétique des Réactions : Résumé
La fréquence des collisions ne détermine pas uniquement la vitesse de la réaction, car pour surmonter l’énergie d’activation nécessaire à la réaction, la température et les concentrations vont également dicter la vitesse de la réaction.
Une augmentation de la température se traduit par des énergies cinétiques plus élevées dans les molécules, ce qui augmente le pourcentage de chances de collision ET de réaction plutôt que de collision et d’inertie. Le fait d’avoir une fréquence de collision constante avec une énergie cinétique plus élevée entraînera une augmentation des vitesses de réaction.
Les catalyseurs incitent les réactifs à réagir entre eux en diminuant l’énergie d’activation de la réaction chimique. Cela peut se faire sans aucune sorte de flux dans l’enthalpie du système.
1) Si les collisions qui se produisent ont suffisamment d’énergie pour dépasser l’énergie d’activation et devenir des produits.
2) Les molécules impliquées dans les collisions sont-elles situées correctement pour que la réaction se produise?
La fréquence des collisions n’augmente pas de façon spectaculaire avec la température; en revanche, le pourcentage de molécules ayant suffisamment d’énergie pour dépasser l’énergie d’activation et devenir des produits augmente.
L’effet net de l’ajout d’un catalyseur est la diminution de la barrière énergétique aux produits. Le catalyseur le fait en permettant un mécanisme alternatif avec une énergie d’activation plus faible.
Vous avez appris que la loi de vitesse intégrée pour chaque type courant de réaction (ordre zéro, premier ou second pour un seul réactif) peut être représentée par une ligne droite. L’utilisation de ces graphiques offre une alternative aux méthodes décrites pour montrer comment la concentration des réactifs évolue avec le temps et déterminer l’ordre de la réaction.
Nous allons illustrer l’utilisation de ces graphiques en considérant la décomposition thermique du gaz NO2 à des températures élevées, qui se produit selon la réaction suivante:
2NO2 (g)Δ → 2NO (g) + O2 (g)
Les données expérimentales pour cette réaction à 330°C sont données dans le tableau ci-dessous; elles sont fournies sous forme de [NO2], ln[NO2], et 1/[NO2] en fonction du temps pour correspondre aux lois de vitesse intégrées pour les réactions d’ordre zéro, de premier et de second ordre, respectivement. Les concentrations actuelles de NO2 sont représentées en fonction du temps dans la partie (a) de la Figure 7.4.1.
|
Temps (s) |
[NO2] (M) |
ln[NO2] |
1/[NO2] (M-1) |
| 0 | 1.00 × 10−2 | -4.605 | 100 |
| 60 | 6.83 × 10−3 | -4.986 | 146 |
| 120 | 5.18 × 10−3 | -5.263 | 193 |
| 180 | 4.18 × 10−3 | -5.477 | 239 |
| 240 | 3.50 × 10−3 | -5.655 | 286 |
| 300 | 3.01 × 10−3 | -5.806 | 332 |
| 360 | 2.64 × 10−3 | -5.937 | 379 |
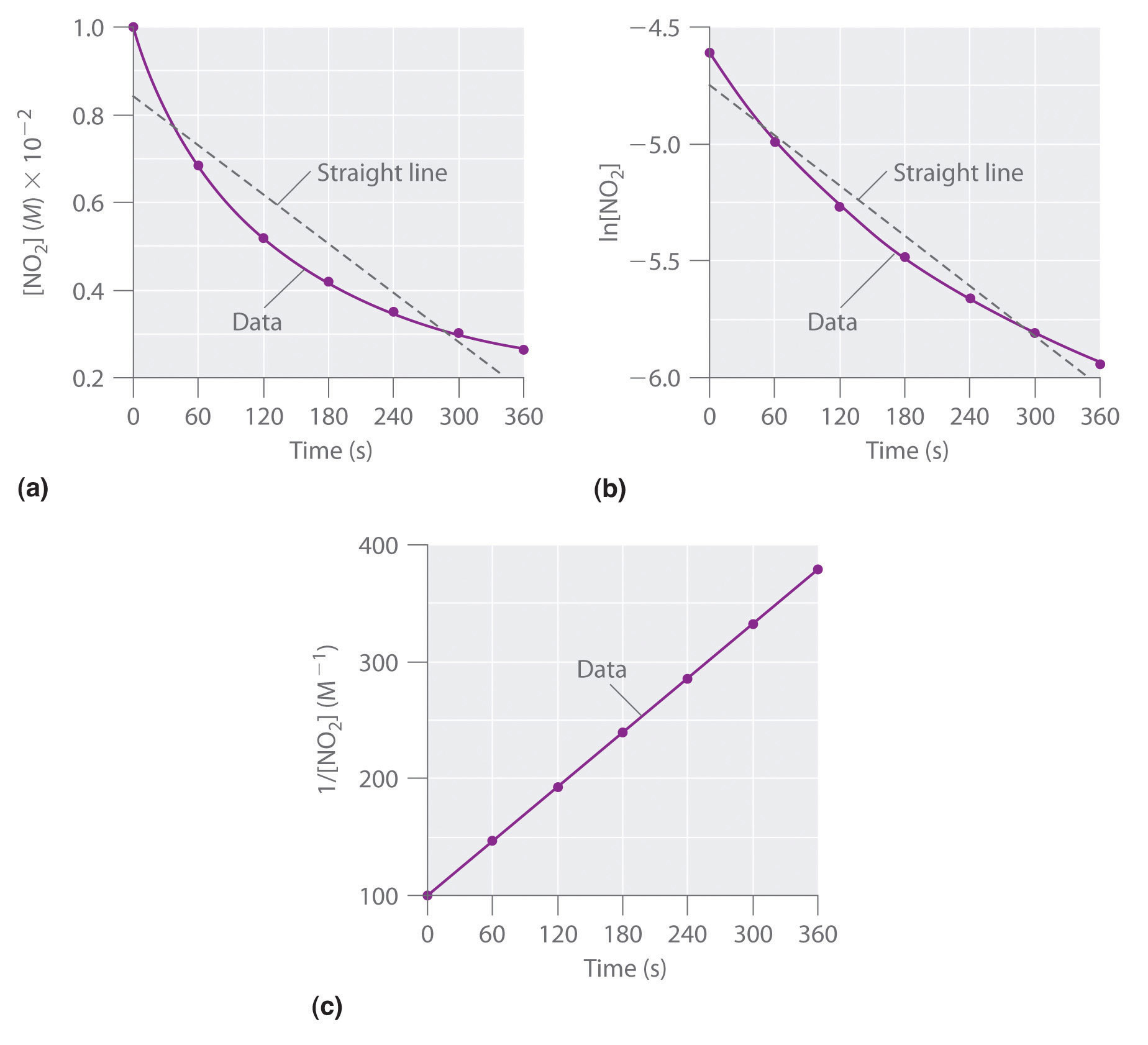
Figure 7.4.1. Ces graphiques montrent la décomposition d’un échantillon de NO2 à 330°C comme (a) la concentration de NO2 en fonction de t, (b) le logarithme naturel de [NO2] en fonction de t, et (c) 1/[NO2] en fonction de t.
Comme le graphique de [NO2] en fonction de t n’est pas une ligne droite, nous savons que la réaction n’est pas d’ordre zéro dans le cas du NO2. Un graphique de ln[NO2] en fonction de t (partie (b) de la Figure 7.4.1) nous montre que la réaction n’est pas du premier ordre dans le NO2 car une réaction du premier ordre donnerait une ligne droite. Après avoir éliminé les comportements d’ordre zéro et de premier ordre, nous construisons un graphique de 1/[NO2] en fonction de t (partie (c) de la Figure 7.4.1). Ce graphique donne une ligne droite, indiquant que la réaction est du second ordre en NO2.
Nous venons de déterminer l’ordre de réaction à partir des données d’une seule expérience en traçant la concentration du réactif en fonction du temps. En raison de la forme caractéristique des courbes illustrées à la Figure 7.4.2, les graphiques peuvent être utilisés pour déterminer l’ordre de réaction d’une réaction inconnue. En revanche, la méthode des vitesses initiales nécessite plusieurs expériences à différentes concentrations de NO2 ainsi que des vitesses initiales de réaction précises, ce qui peut être difficile à obtenir pour les réactions rapides.
|
Ordre zéro Premier ordre Deuxième ordre |
||||||||||||||||||||||||||||||
|
différentielle Vitesse = -Δ[A]Δt=k Vitesse = -Δ[A]Δt=k [A] Vitesse = -Δ[A]Δt=k[A]2 Loi de vitesse |
||||||||||||||||||||||||||||||
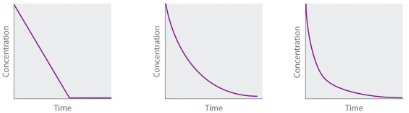
Concentration vs. temps |
||||||||||||||||||||||||||||||
|
Loi de vitesse [A] = [A]0 – kt [A] = [A]0 e-kt1[A] = 1[A]0 + kt intégrée or ln[A] = ln[A]0 – kt
|
||||||||||||||||||||||||||||||
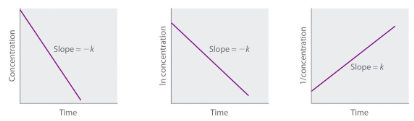
Courbe à ligne droite pour déterminer le constante de vitesse |
||||||||||||||||||||||||||||||
Vitesse relative vs concentration
|
||||||||||||||||||||||||||||||
|
Demi-vie t1/2 = [A]02k t1/2 = 0.693k t1/2 = 1k[A]0 |
||||||||||||||||||||||||||||||
|
Unités de k, M/s 1/s M-1 s-1 constante de vitesse |
||||||||||||||||||||||||||||||
Figure 7.4.2. Propriétés des réactions qui obéissent à des lois de vitesse du zéro, premier et second ordre.
Exemple 7.4.1 – Exemple intégré – Décrire la cinétique d’une réaction
Le pentoxyde de diazote (N2O5) se décompose en NO2 et O2 à des températures relativement basses dans la réaction suivante:
2N2O5 (soln) → 4NO2 (soln) + O2 (g)
Cette réaction est réalisée dans une solution de CCl4 à 45°C. Les concentrations de N2O5 en fonction du temps sont indiquées dans le tableau suivant, ainsi que les logarithmes naturels et les concentrations réciproques de N2O5. Tracer un graphique de la concentration en fonction de t, de ln concentration en fonction de t, et de 1/concentration en fonction de t, puis déterminer la loi de vitesse et calculer la constante de vitesse.
|
Temps (s) |
[N2O5] (M) |
ln [N2O5] |
1/[N2O5] (M-1) |
|
0 |
0,0365 |
-3,310 |
27,4 |
|
600 |
0,0274 |
-3,597 |
36,5 |
|
1200 |
0,0206 |
-3,882 |
48,5 |
|
1800 |
0,0157 |
-4,154 |
63,7 |
|
2400 |
0,0117 |
-4,448 |
85,5 |
|
3000 |
0,00860 |
-4,756 |
116 |
|
3600 |
0,00640 |
-5,051 |
156 |
Solution
Voici les graphiques de [N2O5] en fonction de t, ln[N2O5] en fonction de t, et 1/[ N2O5] en fonction de t:
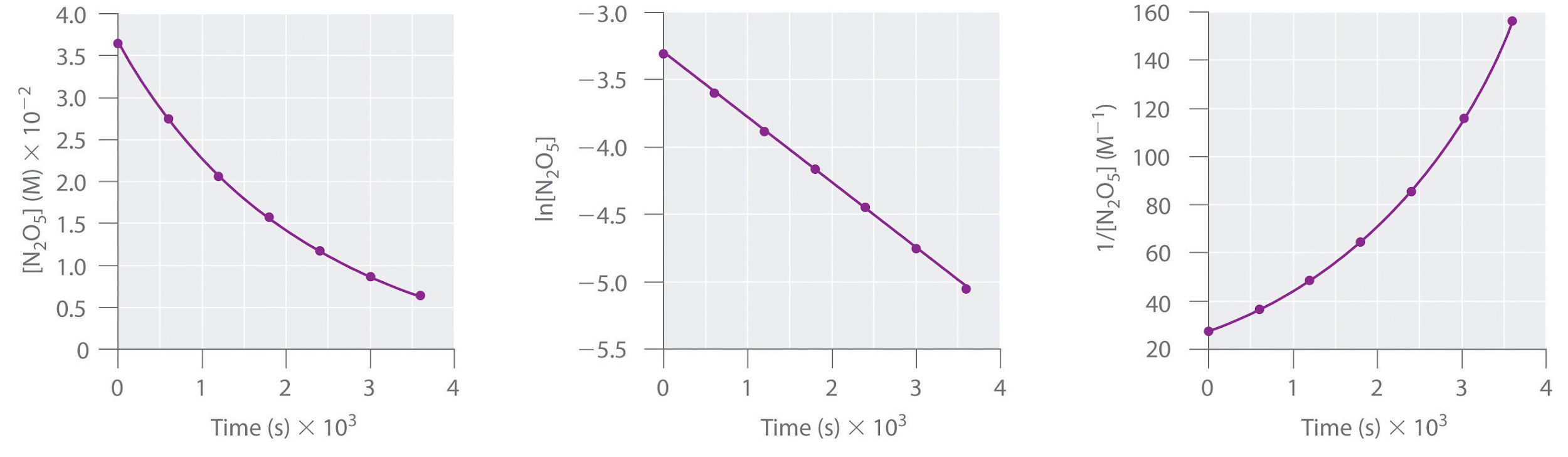
Le graphique de ln[N2O5] en fonction de t donne une ligne droite, alors que les graphiques de [N2O5] en fonction de t et de 1/[N2O5] en fonction de t ne le font pas. Cela signifie que la décomposition de N2O5 est du premier ordre en [N2O5].
La loi de vitesse de la réaction est donc
vitesse = k[N2O5]
Le calcul de la constante de vitesse est simple car nous savons que la pente du graphique de ln[A] en fonction de t pour une réaction du premier ordre est -k. Nous pouvons calculer la pente en utilisant deux points quelconques situés sur la ligne du graphique de ln[N2O5] en fonction de t. En utilisant les points pour t = 0 et 3000 s,
pente = In[N2O5]3000 – In[N2O5]3000s-0s = (-4.756)-(-3.310) 3000s = -4.820×10-4s
Ainsi, k = 4,820 × 10-4 s-1.
Vérifiez votre apprentissage 7.4.1 – Exemple intégré – Décrire la cinétique d’une réaction
Le 1,3-Butadiène (CH2=CH—CH=CH2; C4H6) est une molécule organique volatile et réactive utilisée dans la production de caoutchouc. Au-dessus de la température ambiante, il réagit lentement pour former des produits. Les concentrations de C4H6 en fonction du temps à 326°C sont indiquées dans le tableau suivant, ainsi que le ln [C4H6] et les concentrations réciproques. Tracez un graphique des données sous forme de concentration en fonction de t, de ln concentration en fonction de t et de 1/concentration en fonction de t. Déterminez ensuite l’ordre de réaction du C4H6, la loi de vitesse et la constante de vitesse de la réaction.
|
Temps (s) |
[C4H6] (M) |
ln [C4H6] |
1/[C4H6] (M-1) |
|
0 |
1,72 × 10−2 |
-4,063 |
58,1 |
|
900 |
1,43 × 10−2 |
-4,247 |
69,9 |
|
1800 |
1,23 × 10−2 |
-4,398 |
81,3 |
|
3600 |
9,52 × 10−3 |
-4,654 |
105 |
|
6000 |
7,30 × 10−3 |
-4,920 |
137 |
Réponse
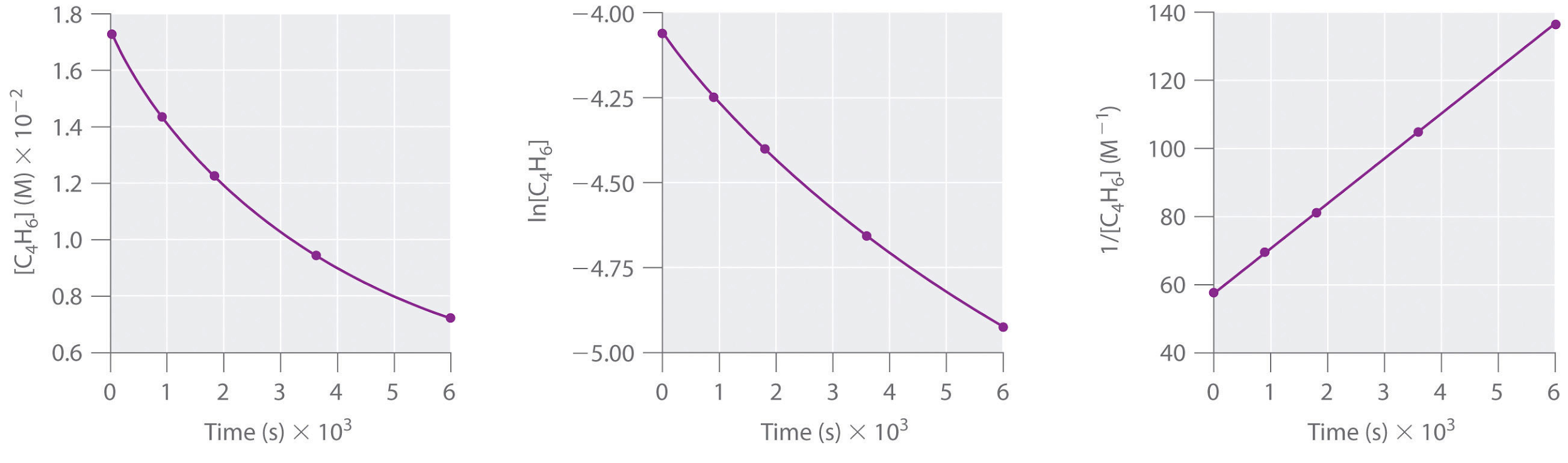
second ordre dans le C4H6; vitesse = k[C4H6]2 ; k = 1,3 × 10-2 M−1·s−1

