7.3 – Lois sur les Taux

Comme décrit dans la section précédente, la vitesse d’une réaction est affectée par les concentrations des réactifs. Les lois ou équations de vitesse sont des expressions mathématiques qui décrivent la relation entre la vitesse d’une réaction chimique et la concentration de ses réactifs. En général, une loi de vitesse (ou loi de vitesse différentielle, comme on l’appelle parfois) prend la forme suivante:

vitesse = k[A]^m[B]ⁿ[C]^p….

dans laquelle [A], [B] et [C] représentent les concentrations molaires des réactifs, et k est la constante de vitesse, qui est spécifique d’une réaction particulière à une température particulière. La valeur numérique de la constante de vitesse est spécifique d’une réaction particulière dans un ensemble donné de conditions, notamment la température, la pression, la phase des réactifs, les solvants, etc. Nous verrons plus loin comment les facteurs individuels influencent la valeur numérique de k. Notez que la valeur numérique de la constante de vitesse est indépendante des concentrations des réactifs A, B ou C, mais nous verrons dans la section suivante comment les unités de k sont affectées par les exposants m, n et p. La valeur numérique de k, cependant, ne change pas au fur et à mesure que la réaction progresse dans un ensemble de conditions donné. Les exposants m, n et p sont généralement des nombres entiers positifs (bien qu’il soit possible qu’ils soient des fractions ou des nombres négatifs). La constante de vitesse k et les exposants m, n et p doivent être déterminés expérimentalement en observant comment la vitesse d’une réaction change lorsque les concentrations des réactifs sont modifiées. Les exposants d’une loi de vitesse décrivent les effets des concentrations des réactifs sur la vitesse de la réaction et définissent l’ordre de la réaction. Considérons une réaction pour laquelle la loi de vitesse est:

vitesse = k[A]^m[B]ⁿ

Si l’exposant m est égal à 1, la réaction est de premier ordre par rapport à A. Si m est égal à 2, la réaction est de second ordre par rapport à A. Si n est égal à 1, la réaction est de premier ordre en B. Si n est égal à 2, la réaction est de second ordre en B. Si m ou n est égal à zéro, la réaction est d’ordre zéro en A ou B, respectivement, et la vitesse de la réaction n’est pas affectée par la concentration de ce réactif. L’ordre global de la réaction est la somme des ordres par rapport à chaque réactif. Si m = 1 et n = 1, l’ordre global de la réaction est du second ordre (m + n = 1 + 1 = 2).

La loi de vitesse:

vitesse = k[H₂O₂]

décrit une réaction qui est du premier ordre dans le peroxyde d’hydrogène et du premier ordre dans l’ensemble. La loi de vitesse:

vitesse = k[C₄H₆]²

décrit une réaction qui est de second ordre dans le C₄H₆ et de second ordre dans l’ensemble. La loi de vitesse:

vitesse = k[H⁺][OH^–]

décrit une réaction qui est de premier ordre pour H⁺, de premier ordre pour OH^–, et de second ordre dans l’ensemble.

Ordre de réaction et unités de constante de vitesse

Parfois, les ordres de réaction dans la loi de vitesse sont les mêmes que les coefficients de l’équation chimique de la réaction. Il s’agit d’une simple coïncidence et, très souvent, ce n’est pas le cas.

Les lois de vitesse peuvent présenter des ordres fractionnaires pour certains réactifs, et des ordres de réaction négatifs sont parfois observés lorsqu’une augmentation de la concentration d’un réactif entraîne une diminution de la vitesse de réaction. Quelques exemples illustrant ces points sont fournis:

2N2O5 (g)  →  4NO2 (g) + O2(g)	Vitesse = k[N2O5]
2NO2 (g) + F2(g)  →  2NO2F (g)	Vitesse = k[NO2][F2]
2H2O2(aq)  →  2H2O (l) + O2(g)	Vitesse = k[H2O2]
H2 (g) + Br2 (g)  →  2HBr (g)	Vitesse = k[H2][Br2]
O3 (g) + CI (g)  →  O2 (g) + CIO (g)	Vitesse = k[O3][CI]

Il est important de noter que les lois de vitesse sont uniquement déterminées expérimentalement et ne sont pas prédites de manière fiable par la stœchiométrie de la réaction. I

Les ordres de réaction jouent également un rôle dans la détermination des unités de la constante de vitesse k. Par exemple, dans une réaction de second ordre, les unités de k sont L mol^-1 s^-1, alors que dans une réaction de troisième ordre, les unités de k sont mol^-2 L²/s. En effet, la vitesse doit toujours être exprimée sous la forme de M/s ou de mol/L•s, et les unités des concentrations individuelles doivent donc correspondre à l’une des unités susmentionnées. De manière plus générale, les unités de la constante de vitesse pour une réaction d’ordre (m + n) sont mol^1−(m+n) L^(m+n)−1 s⁻¹. Le tableau ci-dessous résume les unités de la constante de vitesse pour les ordres de réaction courants.

Constantes de vitesse pour les ordres de réaction courants
Ordre des réactions	Unités de k
(m + n)	mol1−(m+n)L(m+n)−1s−1
zéro	mol/L/s
premier	s-1
deuxième	L/mol/s
troisième	mol2-L2s-1

Tableau 7.3.1 Constantes de vitesse pour les ordres de réaction courants

Notez que les unités du tableau peuvent également être exprimées en termes de molarité (M) au lieu de mol/L. De même, des unités de temps autres que la seconde (comme les minutes, les heures, les jours) peuvent être utilisées, selon la situation.

Exemple 7.3.1 – Écriture de lois de vitesse à partir d’ordres de réaction

Une expérience montre que la réaction du dioxyde d’azote avec le monoxyde de carbone:

NO₂ (g) + CO (g)  →  NO (g) + CO₂ (g)

est d’ordre 2 pour le NO₂ et d’ordre 0 pour le CO à 100°C. Quelle est la loi de vitesse de la réaction? Quelles sont les unités de k?

Solution

La réaction aura la forme:

vitesse = k[NO₂]^m[CO]ⁿ

La réaction est d’ordre 2 pour le NO₂, donc m = 2. La réaction est d’ordre zéro dans le CO; donc n = 0. La loi de vitesse est:

vitesse = k[NO₂]²[CO]⁰ = k[NO₂]²

A partir de là, nous savons que la vitesse doit être exprimée en M/s et que la concentration (au carré) sera exprimée en M², d’où notre valeur k doit être M^-1s^-1.

Rappelez-vous qu’un nombre élevé à la puissance zéro est égal à 1, donc [CO]⁰ = 1. C’est pourquoi nous pouvons tout simplement supprimer la concentration de CO de l’équation de vitesse: la vitesse de réaction dépend uniquement de la concentration de NO₂. Lorsque nous étudierons les mécanismes de vitesse plus tard dans ce chapitre, nous expliquerons comment la concentration d’un réactif peut n’avoir aucun effet sur une réaction bien qu’il soit impliqué dans la réaction.

Vérifiez votre apprentissage 7.3.1- Écriture de lois de vitesse à partir d’ordres de réaction

La loi de la vitesse de la réaction:

H₂ (g) + 2NO (g) → N₂O (g) + H₂O (g)

a été déterminée comme étant la vitesse = k[NO]²[H₂]. Quels sont les ordres par rapport à chaque réactif, et quel est l’ordre global de la réaction?

Réponse

ordre dans NO = 2; ordre dans H₂ = 1; ordre global = 3

Vérifiez votre apprentissage 7.3.2 – Écriture de lois de vitesse à partir d’ordres de réaction

Dans une réaction de transestérification, un triglycéride réagit avec un alcool pour former un ester et du glycérol. De nombreux élèves découvrent la réaction entre le méthanol (CH₃OH) et l’acétate d’éthyle (CH₃CH₂OCOCH₃) comme exemple de réaction avant d’étudier les réactions chimiques qui produisent le biodiesel:

CH₃OH+CH₃CH₂OCOCH₃  →  CH₃OCOCH₃ + CH₃CH₂OH

La loi de vitesse de la réaction entre le méthanol et l’acétate d’éthyle est, dans certaines conditions, déterminée comme étant:

vitesse = k[CH₃OH]

Quel est l’ordre de réaction par rapport au méthanol et à l’acétate d’éthyle, et quel est l’ordre global de réaction?

Réponse

ordre dans CH₃OH = 1; ordre dans CH₃CH₂OCOCH₃ = 0; ordre global = 1

Exemple 7.3.2 – Interprétation des lois de vitesse

Vous trouverez ci-dessous trois réactions et leurs lois de vitesse différentielle déterminées expérimentalement. Pour chaque réaction, donnez les unités de la constante de vitesse, donnez l’ordre de la réaction par rapport à chaque réactif, donnez l’ordre global de la réaction, et prédisez ce qui arrive à la vitesse de la réaction lorsque la concentration de la première espèce dans chaque équation chimique est doublée.

Solution

(a) [HI]² donnera des unités de (moles par litre)². Pour que la vitesse de réaction ait des unités de moles par litre par seconde, la constante de vitesse doit avoir des unités réciproques

L’exposant de la loi de vitesse est 2, donc la réaction est de second ordre en HI. Parce que HI est le seul réactif et la seule espèce qui apparaît dans la loi de vitesse, la réaction est aussi globalement du second ordre.

Si la concentration de HI est doublée, la vitesse de réaction passe de k[HI]₀² à k(2[HI])₀² = 4k[HI]₀². La vitesse de réaction va donc quadrupler.

(b) Parce qu’aucun terme de concentration n’apparaît dans la loi de vitesse, la constante de vitesse doit avoir des unités M/s pour que la vitesse de réaction ait des unités M/s.
La loi de vitesse nous indique que la vitesse de réaction est constante et indépendante de la concentration de
N₂O. Autrement dit, la réaction est d’ordre zéro dans le N₂O et d’ordre zéro dans l’ensemble. Comme la vitesse de réaction est indépendante de la concentration de N₂O, doubler la concentration n’aura aucun effet sur la vitesse de réaction.

(c) La loi de vitesse ne contient qu’un seul terme de concentration élevé à la première puissance. Par conséquent, la constante de vitesse doit avoir des unités de secondes réciproques (s^-1) pour avoir des unités de moles par litre par seconde pour la vitesse de réaction : M·s⁻¹ = M/s.

La seule concentration dans la loi de vitesse est celle du cyclopropane, et son exposant est de 1. Cela signifie que la réaction est du premier ordre pour le cyclopropane. Le cyclopropane est la seule espèce qui apparaît dans la loi de vitesse, donc la réaction est aussi globalement du premier ordre.

En doublant la concentration initiale de cyclopropane, la vitesse de réaction passe de k[cyclopropane]₀ à 2k[cyclopropane]₀. La vitesse de réaction est donc doublée.

Vérifiez votre apprentissage 7.3.3 – Interprétation des lois de vitesse

Étant donné les deux réactions suivantes et leurs lois de vitesse différentielle déterminées expérimentalement: déterminez les unités de la constante de vitesse si le temps est en secondes, déterminez l’ordre de réaction par rapport à chaque réactif, donnez l’ordre de réaction global et prédisez ce qui arrivera à la vitesse de réaction lorsque la concentration de la première espèce dans chaque équation est doublée.

avec

avec

vitesse = -Δ[F₂]Δt = -12(Δ[NO₂]Δt) = k[NO₂][F₂]

Réponse

(a) s^-1; premier ordre dans CH₃N=NCH₃; premier ordre global; doubler [CH₃N=NCH₃] doublera la vitesse de réaction.

(b) M^-1·s⁻¹; premier ordre pour NO₂, premier ordre pour F₂; deuxième ordre dans l’ensemble; le doublement de [NO₂] doublera la vitesse de réaction.

Cinétique expérimentale – Méthode des vitesses initiaux

Le nombre de mécanismes fondamentalement différents (ensembles d’étapes d’une réaction) est en fait assez faible par rapport au grand nombre de réactions chimiques qui peuvent se produire. Ainsi, la compréhension des mécanismes de réaction peut simplifier ce qui peut sembler être une variété confuse de réactions chimiques. La première étape de la découverte du mécanisme réactionnel consiste à déterminer la loi de vitesse de la réaction. Pour ce faire, on peut concevoir des expériences qui mesurent la ou les concentrations d’un ou plusieurs réactifs ou produits en fonction du temps.

Pour la réaction A + B → produits, par exemple, nous devons déterminer k et les exposants m et n dans l’équation suivante:

vitesse = k[A]^m[B]ⁿ

Équation 7.3.1 Équation de la loi de vitesse

Nous pouvons utiliser une méthode algébrique explicite, souvent appelée méthode des vitesses initiaux, pour déterminer les ordres dans les lois de vitesse. Pour utiliser cette méthode, nous sélectionnons deux ensembles de données de vitesses qui diffèrent par la concentration d’un seul réactif et établissons un rapport entre les deux vitesses et les deux lois de vitesse. Après avoir annulé les termes qui sont égaux, il nous reste une équation qui ne contient qu’une seule inconnue, le coefficient de la concentration qui varie. Nous résolvons ensuite cette équation pour obtenir ce coefficient. Les données de vitesse pour une réaction hypothétique du type A + B → produits sont données dans le tableau ci-dessous.

Expérience	[A] (M)	[B] (M)	Vitesse initiale (M/min)
1	0,50	0,50	8,5 × 10-3
2	0,75	0,50	19 × 10-3
3	1,00	0,50	34 × 10-3
4	0,50	0,75	8,5 × 10-3
5	0,50	1,00	8,5 × 10-3

Tableau 7.3.2 Vitesse initial à concentration

La loi de vitesse générale pour la réaction est

vitesse = k[A]^m[B]ⁿ

Équation 7.3.2Loi de vitesse générale

Nous pouvons obtenir m ou n directement en utilisant une proportion des lois de vitesse pour deux expériences dans lesquelles la concentration d’un réactif est la même, comme les expériences 1 et 3 du tableau ci-dessus.

vitesse₁vitesse₃ = k[A₁]^m[B₁]ⁿk[A₃]^m[B₃]ⁿ

Insérer les valeurs appropriées du tableau,

8.5 × 10^-3 M / min 34×10^-3 M / min = k[0.50M]^m[0.50M]ⁿk[1.00M]^m[0.50M]ⁿ

Comme 1,00 à toute puissance est égal à 1, [1,00 M]^m = 1,00 M. Nous pouvons annuler les termes semblables pour obtenir 0,25 = [0,50]^m, ce qui peut également s’écrire 1/4 = [1/2]^m. Nous pouvons donc conclure que m = 2 et que la réaction est de second ordre en A. En choisissant deux expériences dans lesquelles la concentration de B est la même, nous avons pu résoudre la question de m.

Inversement, en choisissant deux expériences dans lesquelles la concentration de A est la même (par exemple, les expériences 5 et 1), nous pouvons résoudre n.

vitesse₁vitesse₅ = k[A₁]^m[B₁]ⁿk[A₅]^m[B₅]ⁿ

En substituant les valeurs appropriées du tableau,

8.5 × 10^-3 M / min 8.5 × 10^-3 M / min = k[0.50M]^m[0.50M]ⁿk[0.50M]^m[1.00M]ⁿ

L’annulation laisse 1,0 = [0,50]ⁿ, ce qui donne n = 0; c’est-à-dire que la réaction est d’ordre zéro en B. La loi de vitesse déterminée expérimentalement est donc la suivante

vitesse = k[A]²[B]⁰ = k[A]²

Nous pouvons maintenant calculer la constante de vitesse en insérant les données de n’importe quelle ligne du tableau dans la loi de vitesse déterminée expérimentalement et en résolvant pour k. En utilisant l’Expérience 2, nous obtenons

19 × 10⁻³ M/min = k(0.75 M)²

3.4 × 10⁻² M⁻¹·min⁻¹ = k

Vous devez vérifier que l’utilisation des données de toute autre ligne du tableau donne la même constante de vitesse. Cela doit être vrai tant que les conditions expérimentales, telles que la température et le solvant, sont les mêmes.

Exemple 7.3.3 – Détermination d’une loi de vitesse à partir des vitesses initiales – 1

L’ozone dans la haute atmosphère s’appauvrit lorsqu’il réagit avec les oxydes d’azote. Les vitesses des réactions des oxydes d’azote avec l’ozone sont des facteurs importants pour déterminer l’importance de ces réactions dans la formation du trou d’ozone au-dessus de l’Antarctique (Figure 7.3.7). L’une de ces réactions est la combinaison de l’oxyde nitrique, NO, avec l’ozone, O₃:

NO (g) + O₃ (g)  →  NO₂ (g) + O₂ (g)

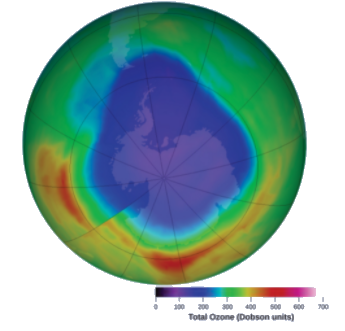
Figure 7.3.1. Au cours des dernières années, la concentration d’ozone atmosphérique au-dessus de l’Antarctique a diminué pendant l’hiver. Cette carte montre la diminution de la concentration sous la forme d’une zone violette. (crédit: modification du travail de la NASA) 

Cette réaction a été étudiée en laboratoire, et les données de vitesse suivantes ont été déterminées à 25°C.

Essai	[NO] (mol/L)	[O3] (mol/L)	Δ[NO2]Δt (mol L-1 s-1)
1	1,00 × 10−6	3,00 × 10−6	6,60 × 10−5
2	1,00 × 10−6	6,00 × 10−6	1,32 × 10−4
3	1,00 × 10−6	9,00 × 10−6	1,98 × 10−4
4	2,00 × 10−6	9,00 × 10−6	3,96 × 10−4
5	3,00 × 10−6	9,00 × 10−6	5,94 × 10−4

Déterminez la loi de vitesse et la constante de vitesse pour la réaction à 25°C.

Solution

La loi de vitesse aura la forme:

vitesse = k[NO]^m[O₃]ⁿ

Nous pouvons déterminer les valeurs de m, n et k à partir des données expérimentales en utilisant le processus à trois parties suivantes:

1. Déterminez la valeur de m à partir des données dans lesquelles [NO] varie et [O₃] est constant. Dans les trois dernières expériences, [NO] varie alors que [O₃] reste constant. Lorsque [NO] double entre les essais 3 et 4, la vitesse double, et lorsque [NO] triple entre les essais 3 et 5, la vitesse triple également. Ainsi, la vitesse est également directement proportionnel à [NO], et m dans la loi de vitesse est égal à 1.

2. Déterminez la valeur de n à partir de données dans lesquelles [O₃] varie et [NO] est constant. Dans les trois premières expériences, [NO] est constant et [O₃] varie. La vitesse de réaction change en proportion directe avec le changement de [O₃]. Lorsque [O₃] double de l’essai 1 à 2, la vitesse double; lorsque [O₃] triple de l’essai 1 à 3, la vitesse augmente également de trois fois. Ainsi, la vitesse est directement proportionnelle à [O₃], et n est égal à 1. La loi de vitesse est donc:

vitesse = k[NO]¹[O₃]¹ = K[NO][O₃]

3. Déterminez la valeur de k à partir d’une série de concentrations et de la vitesse correspondante.

La grande valeur de k nous indique qu’il s’agit d’une réaction rapide qui pourrait jouer un rôle important dans l’appauvrissement de la couche d’ozone si [NO] est suffisamment important.

Vérifiez votre apprentissage 7.3.4 – Détermination d’une loi de vitesse à partir des vitesses initiales – 1

L’acétaldéhyde se décompose lorsqu’il est chauffé pour donner du méthane et du monoxyde de carbone selon l’équation suivante:

CH₃CHO (g)  →  CH₄ (g) + CO (g)

Déterminez la loi et la constante de vitesse de la réaction à partir des données expérimentales suivantes:

Essai	[CH3CHO] (mol/L)	-Δ[CH3CHO]Δt (mol L-1 s-1)
1	1,75 × 10−3	2,06 × 10−11
2	3,50 × 10−3	8,24 × 10−11
3	7,00 × 10−3	3,30 × 10−10

Réponse

vitesse = k[CH₃CHO]² avec k = 6,73 × 10^-6 L/mol/s

Exemple 7.3.4 – Détermination d’une loi de vitesse à partir des vitesses initiales – 2

L’oxyde nitrique est produit dans l’organisme par plusieurs enzymes différentes et agit comme un signal qui contrôle la pression sanguine, la mémoire à long terme et d’autres fonctions essentielles. La principale voie d’élimination du NO des fluides biologiques est la réaction avec O₂ pour donner du NO₂, qui réagit ensuite rapidement avec l’eau pour donner de l’acide nitreux et de l’acide nitrique:

2NO + O₂  →  2NO₂

Ces réactions sont importantes pour maintenir des niveaux stables de NO. Le tableau suivant présente les données cinétiques de la réaction de NO avec O₂ à 25°C:

2NO (g) + O₂ (g) → 2NO₂ (g)

Déterminez la loi de vitesse de la réaction et calculez la constante de vitesse.

Solution

La comparaison des expériences 1 et 2 montre que lorsque [O₂] est doublé pour une valeur constante de [NO₂], la vitesse de réaction double approximativement. La vitesse de réaction est donc proportionnelle à [O₂]¹, la réaction est donc du premier ordre en O₂. La comparaison des expériences 1 et 3 montre que la vitesse de réaction quadruple essentiellement lorsque [NO] est doublé et que [O₂] est maintenu constant. C’est-à-dire que la vitesse de réaction est proportionnelle à [NO]², ce qui indique que la réaction est du second ordre pour le NO. En utilisant ces relations, nous pouvons écrire la loi de vitesse de la réaction:

vitesse = k[NO]²[O₂]. Les données de chaque ligne peuvent être utilisées pour calculer la constante de vitesse. En utilisant l’expérience 1, par exemple, on obtient

k = vitesse[NO]²[O²] = 7.98 x 10^-3 M / s [0.0235M]²[0.0125M] = 1.16 x 10³ M^-2・s^-1

Alternativement, en utilisant l’expérience 2, on obtient

k = vitesse[NO]²[O²] = 15.9 x 10^-3 M / s [0.0235M]²[0.0250M] = 1.15 x 10³ M^-2・s^-1

La différence est mineure et associée à des chiffres significatifs et à une probable erreur expérimentale dans la réalisation du tableau.

L’ordre de réaction global (m + n) = 3, il s’agit donc d’une réaction du troisième ordre dont la vitesse est déterminée par trois réactifs. Les unités de la constante de vitesse deviennent plus complexes lorsque l’ordre global de la réaction augmente.

Vérifiez votre apprentissage 7.3.5 – Détermination d’une loi de vitesse à partir des vitesses initiales – 2

L’ion peroxydisulfate (S₂O₈²⁻) est un puissant agent oxydant qui réagit rapidement avec l’ion iodure dans l’eau:

S₂O₈^2- (aq) + 3I^1- (aq) → 2SO₄^2- (aq) + I₃^– (aq)

Le tableau suivant présente les données cinétiques de cette réaction à 25°C. Déterminez la loi de vitesse et calculez la constante de vitesse.

Expérience	[S2O82-]0 (M)	[I–]0 (M)	Vitesse initiale (M/s)
1	0,27	0,38	2,05
2	0,40	0,38	3,06
3	0,40	0,22	1,76

Réponse

vitesse = k[S₂O₈²⁻][I⁻]; k = 20 M⁻¹·s⁻¹

Lois sur les vitesses intégrées

Les lois de vitesse que nous avons vues jusqu’à présent relient la vitesse et les concentrations des réactifs. Nous pouvons également déterminer une deuxième forme de chaque loi de vitesse qui relie les concentrations des réactifs et le temps. Ces lois sont appelées lois de vitesses intégrées. Nous pouvons utiliser une loi de vitesse intégrée pour déterminer la quantité de réactif ou de produit présente après un certain temps ou pour estimer le temps nécessaire pour qu’une réaction se déroule dans une certaine mesure. Par exemple, une loi de vitesse intégrée est utilisée pour déterminer la durée du stockage d’un matériau radioactif pour que sa radioactivité se désintègre à un niveau sûr.

En utilisant le calcul, la loi de vitesse différentielle pour une réaction chimique peut être intégrée par rapport au temps pour donner une équation qui relie la quantité de réactif ou de produit présent dans un mélange réactionnel au temps écoulé de la réaction. Ce processus peut être soit très simple, soit très complexe, en fonction de la complexité de la loi de vitesse différentielle. Pour les besoins de la discussion, nous nous concentrerons sur les lois de vitesse intégrées résultantes pour les réactions d’ordre zéro, premier et second.

De plus, nous allons étudier le cas de la demi-vie pour ces réactions d’ordres différents. La demi-vie d'une réaction (t_1/2) est le temps nécessaire pour que la moitié d’une quantité donnée de réactif soit consommée. À chaque demi-vie suivante, la moitié de la concentration restante du réactif est consommée. En utilisant la décomposition du peroxyde d’hydrogène comme exemple, nous constatons que pendant la première demi-vie (de 0,00 heure à 6,00 heures), la concentration de H₂O₂ diminue de 1,000 M à 0,500 M. Pendant la deuxième demi-vie (de 6,00 heures à 12,00 heures), elle diminue de 0,500 M à 0,250 M; pendant la troisième demi-vie, elle diminue de 0,250 M à 0,125 M. La concentration de H₂O₂ diminue de moitié pendant chaque période successive de 6,00 heures. La décomposition du peroxyde d’hydrogène est une réaction de premier ordre et, comme on peut le montrer, la demi-vie d’une réaction de premier ordre est indépendante de la concentration du réactif. Cependant, les demi-vies des réactions d’autres ordres dépendent des concentrations des réactifs.

Réactions d’ordre zéro

Pour les réactions d’ordre zéro, la loi de vitesse différentielle est:

Vitesse = k[A]⁰ = k

Équation 7.3.3 Loi de vitesse différentielle d’ordre zéro

Une réaction d’ordre zéro présente donc une vitesse de réaction constante, quelle que soit la concentration de ses réactifs.

[A] = –kt + [A]₀

y = mx + b

Comme la vitesse est indépendante de la concentration du réactif, le graphique de la concentration de tout réactif en fonction du temps est une ligne droite avec une pente de -k. La valeur de k est négative car la concentration du réactif diminue avec le temps. Inversement, le graphique de la concentration d’un produit quelconque en fonction du temps est une ligne droite avec une pente de k, une valeur positive.

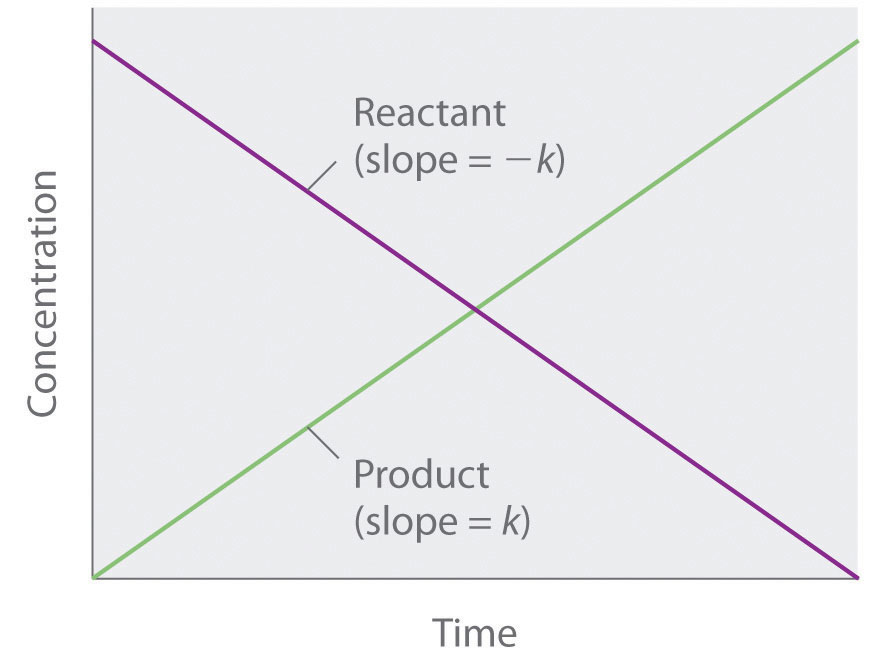
Figure 7.3.2. Le graphique d’une réaction d’ordre zéro. La variation de la concentration du réactif et du produit en fonction du temps produit une ligne droite. 

La loi de vitesse intégrée pour une réaction d’ordre zéro produit également une ligne droite et a la forme générale suivante

[A] = [A]₀ – kt

où [A]₀ est la concentration initiale du réactif A. L’équation ci-dessus a la forme de l’équation algébrique pour une ligne droite, y = mx + b, avec y = [A], mx = –kt, et b = [A]₀). Dans une réaction d’ordre zéro, la constante de vitesse doit avoir les mêmes unités que la vitesse de réaction, généralement des moles par litre par seconde.

Bien qu’il puisse sembler contre-intuitif que la vitesse de réaction soit indépendante de la concentration du ou des réactifs, de telles réactions sont plutôt courantes. Elles se produisent le plus souvent lorsque la vitesse de réaction est déterminée par la surface disponible. Un exemple est la décomposition de N₂O sur une surface de platine (Pt) pour produire N₂ et O₂, qui se produit à des températures allant de 200°C à 400°C:

2N₂O (g)

Sans surface de platine, la réaction nécessite des températures supérieures à 700°C, mais entre 200°C et 400°C, le seul facteur qui détermine la vitesse de décomposition du N₂O est la quantité de surface de Pt disponible (et non la quantité de Pt). Tant qu’il y a suffisamment de N₂O pour réagir avec toute la surface de Pt, doubler ou quadrupler la concentration de N₂O n’aura aucun effet sur la vitesse de réaction. À de très faibles concentrations de N₂O, où il n’y a pas assez de molécules présentes pour occuper la totalité de la surface de Pt disponible, la vitesse de réaction dépend de la concentration de N₂O. La vitesse de réaction est la suivante:

Ainsi, la vitesse à laquelle N₂O est consommée et les vitesses auxquelles N₂ et O₂ sont produits sont indépendantes de la concentration. Comme le montre la Figure 7.3.3 ci-dessous, l’évolution des concentrations de toutes les espèces en fonction du temps est linéaire. Plus important encore, l’exposant (0), correspondant à la concentration de N₂O dans la loi de vitesse dérivée expérimentalement, n’est pas le même que le coefficient stœchiométrique du réactif dans l’équation chimique équilibrée (2). Pour cette réaction, comme pour toutes les autres, la loi de vitesse doit être déterminée expérimentalement.

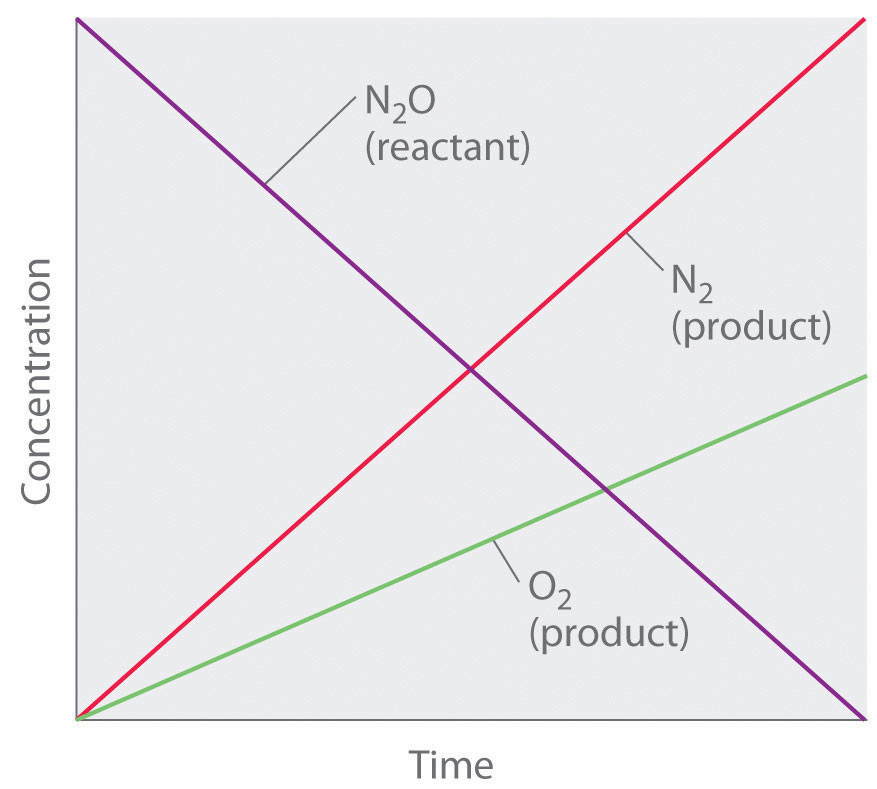
Figure 7.3.3. Ce graphique montre les concentrations des réactifs et des produits en fonction du temps pour la décomposition catalysée d’ordre zéro de N₂O en N₂ et O₂ sur une surface de Pt. L’évolution des concentrations de toutes les espèces en fonction du temps est linéaire. 

Une réaction d’ordre zéro qui a lieu dans le foie humain est l’oxydation de l’éthanol (des boissons alcoolisées) en acétaldéhyde, catalysée par l’enzyme alcool déshydrogénase. À des concentrations élevées d’éthanol, cette réaction est également une réaction d’ordre zéro. L’équation globale de la réaction est la suivante

CH₃CH₂OH + NAD⁺

où NAD+ (nicotinamide adénine dinucléotide) et NADH (nicotinamide adénine dinucléotide réduit) sont respectivement les formes oxydée et réduite d’une espèce utilisée par tous les organismes pour transporter les électrons. Lorsqu’on consomme une boisson alcoolisée, l’éthanol est rapidement absorbé dans le sang. Sa concentration diminue ensuite à un rythme constant jusqu’à atteindre zéro (partie (a) de la Figure 7.3.4). Une personne de 70 kg met en moyenne 2,5 heures pour oxyder les 15 mL d’éthanol contenus dans une canette de bière de 12 oz, un verre de vin de 5 oz ou un verre de spiritueux (whisky ou brandy). La vitesse réelle, cependant, varie beaucoup d’une personne à l’autre, en fonction de la taille du corps et de la quantité d’alcool déshydrogénase dans le foie. La vitesse de réaction n’augmente pas si une plus grande quantité d’alcool est consommée au cours de la même période de temps, car la vitesse de réaction est déterminée uniquement par la quantité d’enzyme présente dans le foie. Contrairement à la croyance populaire, la caféine contenue dans le café est inefficace pour catalyser l’oxydation de l’éthanol. Lorsque l’éthanol a été complètement oxydé et que sa concentration tombe pratiquement à zéro, la vitesse d’oxydation chute également rapidement (partie (b) de la Figure 7.3.4).

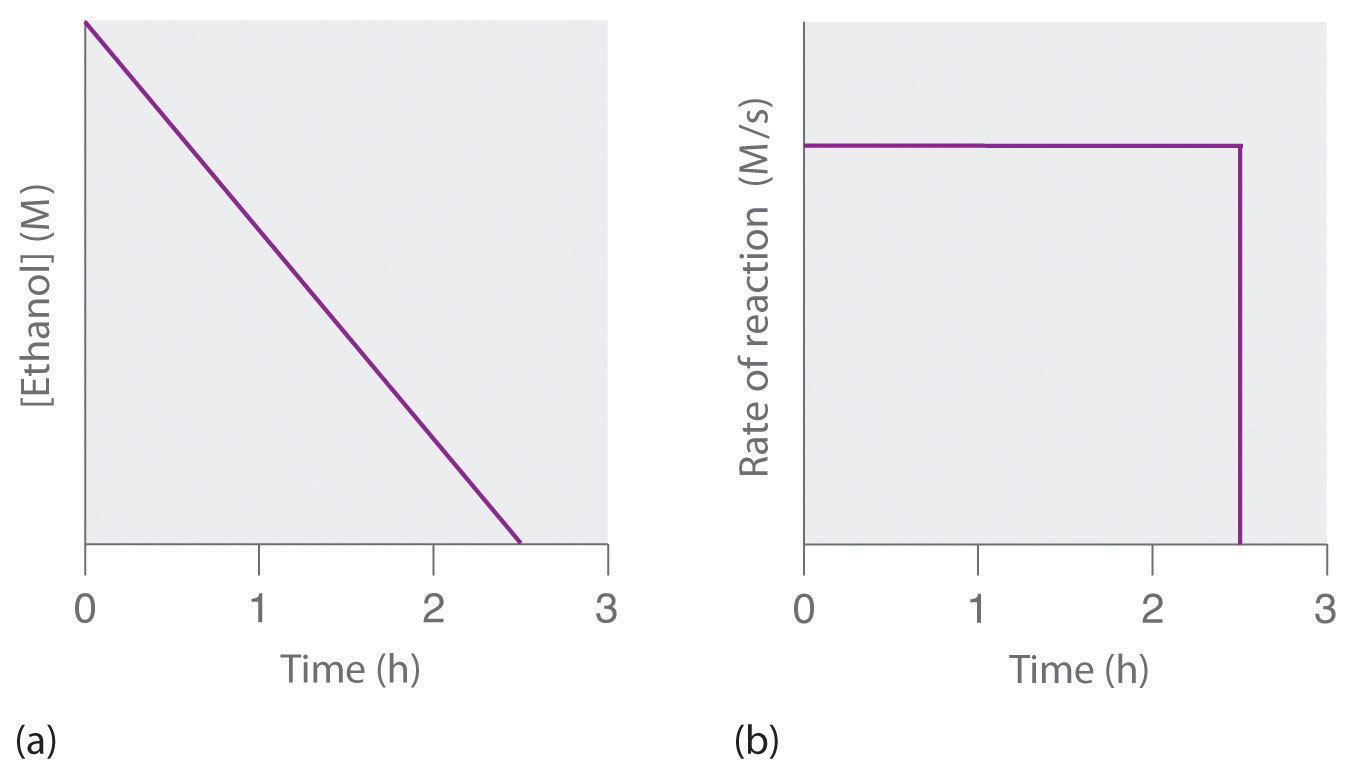
Figure 7.3.4.Oxydation catalysée de l’éthanol (a) La concentration d’éthanol dans le sang humain diminue linéairement avec le temps, ce qui est typique d’une réaction d’ordre zéro. (b) La vitesse d’oxydation de l’éthanol est constante jusqu’à ce que la concentration d’éthanol atteigne pratiquement zéro, moment auquel la vitesse de réaction tombe à zéro.

Ces exemples illustrent deux points importants:

Dans une réaction d’ordre zéro, la vitesse de réaction ne dépend pas de la concentration du réactif.

Une variation linéaire de la concentration en fonction du temps est une indication claire d’une réaction d’ordre zéro.

Demi-vie des réactions d’ordre zéro

Nous pouvons dériver une équation pour calculer la demi-vie d’une réaction d’ordre zéro comme suit:

[A] = –kt + [A]₀

Lorsque la moitié de la quantité initiale de réactif a été consommée, t = t_1/2 et [A] = [A]₀²

Ainsi:

et

t_1/2 = [A]₀²k

La demi-vie d’une réaction d’ordre zéro augmente lorsque la concentration initiale augmente; par conséquent, sa demi-vie dépend de la concentration.

Réactions du premier ordre

Dans une réaction du premier ordre, la vitesse de réaction est directement proportionnelle à la concentration de l’un des réactifs. Les réactions du premier ordre ont souvent la forme générale A → produits. La vitesse différentielle d’une réaction du premier ordre est la suivante:

vitesse = -Δ[A]Δt = k[A]

Si la concentration de A est doublée, la vitesse de réaction double; si la concentration de A est augmentée d’un facteur 10, la vitesse de réaction augmente d’un facteur 10, et ainsi de suite. Comme les unités de la vitesse de réaction sont toujours des moles par litre par seconde, les unités d’une constante de vitesse du premier ordre sont des secondes réciproques (s^-1).

La loi de vitesse intégrée pour une réaction du premier ordre peut être écrite de deux manières différentes: l’une utilisant les exposants et l’autre les logarithmes. La forme exponentielle est la suivante:

[A] = [A]₀e^-kt

où [A]₀ est la concentration initiale du réactif A à t = 0; k est la constante de vitesse; et e est la base des logarithmes naturels, qui a la valeur 2,718 à trois décimales près. Rappelons qu’une loi de vitesse intégrée donne la relation entre la concentration du réactif et le temps. L’équation ci-dessus prédit que la concentration de A diminuera dans le temps selon une courbe exponentielle régulière. En prenant le logarithme naturel de chaque côté de l’équation et en réorganisant, nous obtenons une autre expression logarithmique de la relation entre la concentration de A et t:

ln[A] = ln[A]₀ – kt

Comme cette équation a la forme de l’équation algébrique d’une ligne droite, y = mx + b, avec y = ln [A] et b = ln[A]₀, un graphique de ln [A] en fonction de t pour une réaction du premier ordre devrait donner une ligne droite avec une pente de -k et un point d’interception de ln[A]₀. On peut utiliser soit la loi de vitesse différentielle, soit la loi de vitesse intégrée pour déterminer si une réaction particulière est du premier ordre.

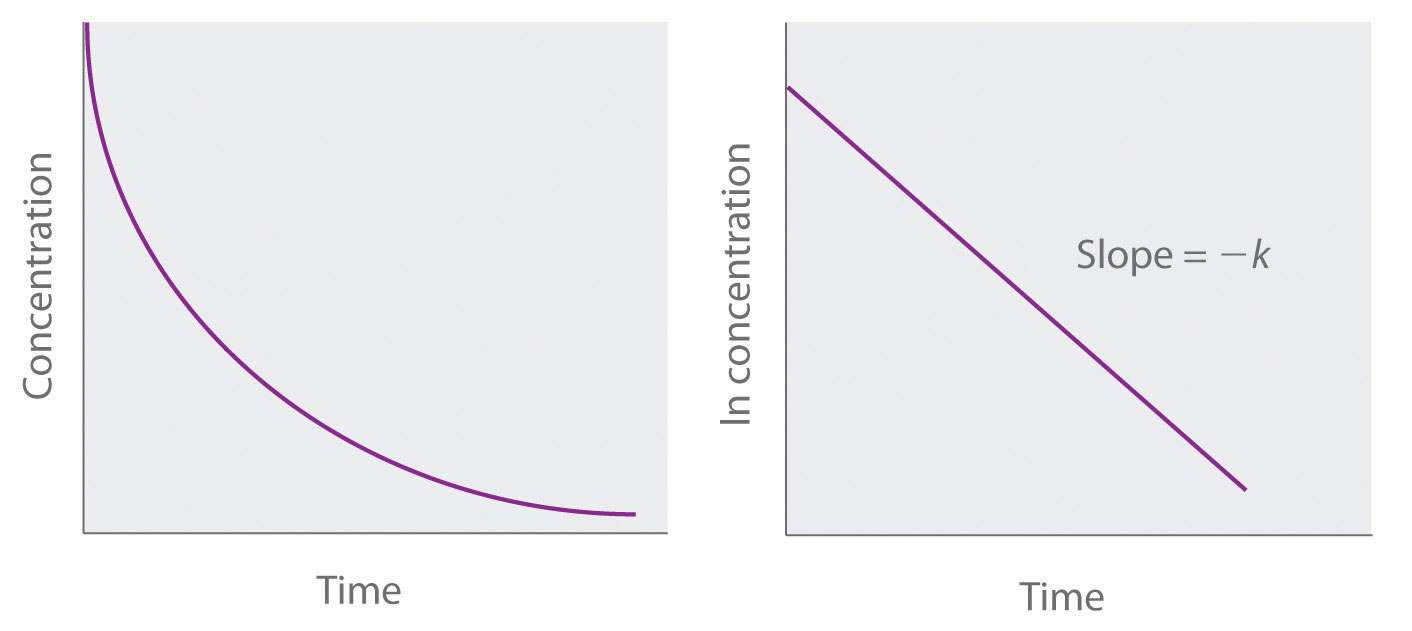
Figure 7.3.5. Graphiques d’une réaction du premier ordre. Les formes attendues des courbes pour les graphiques de la concentration du réactif en fonction du temps (en haut) et du logarithme naturel de la concentration du réactif en fonction du temps (en bas) pour une réaction du premier ordre. 

Les réactions du premier ordre sont très courantes. Une réaction qui présente une cinétique de premier ordre apparente est l’hydrolyse du cisplatine, un médicament anticancéreux.

Le cisplatine, premier médicament anticancéreux “inorganique” à avoir été découvert, est unique par sa capacité à provoquer une rémission complète des cancers relativement rares, mais mortels, des organes reproducteurs chez les jeunes adultes. Les structures du cisplatine et de son produit d’hydrolyse sont les suivantes:

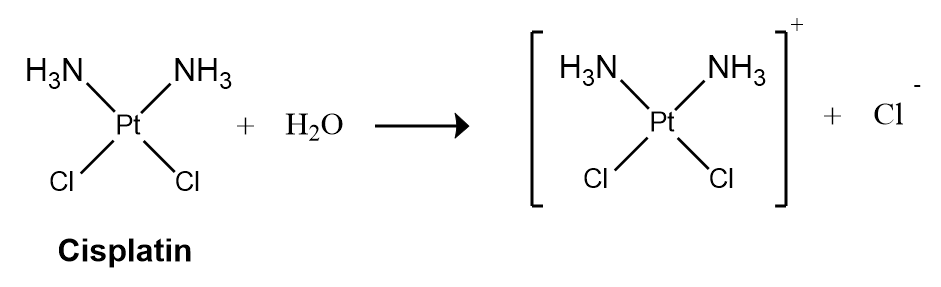
Les deux composés du platine possèdent quatre groupes disposés dans un plan carré autour d’un ion Pt(II). La réaction présentée ci-dessus est importante car le cisplatine, la forme sous laquelle le médicament est administré, n’est pas la forme sous laquelle le médicament est actif. Au contraire, au moins un ion chlorure doit être remplacé par de l’eau pour produire une espèce qui réagit avec l’acide désoxyribonucléique (ADN) pour empêcher la division cellulaire et la croissance tumorale. Par conséquent, la cinétique de la réaction a été étudiée de manière approfondie afin de trouver des moyens de maximiser la concentration de l’espèce active.

La loi de vitesse et l’ordre de réaction de l’hydrolyse du cisplatine sont déterminés à partir de données expérimentales, telles que celles présentées dans le tableau ci-dessous. Le tableau présente les données de vitesse initiale pour quatre expériences dans lesquelles la réaction a été réalisée à pH 7,0 et à 25°C, mais avec différentes concentrations initiales de cisplatine. Comme la vitesse de réaction augmente avec la concentration de cisplatine, nous savons qu’il ne peut s’agir d’une réaction d’ordre zéro. La comparaison des expériences 1 et 2 dans le tableau montre que la vitesse de réaction double [(1,8 × 10^-5 M/min) ÷ (9,0 × 10^-6 M/min) = 2,0] lorsque la concentration de cisplatine est doublée (de 0,0060 M à 0,012 M). De même, la comparaison des expériences 1 et 4 montre que la vitesse de réaction augmente d’un facteur 5 [(4,5 × 10^-5 M/min) ÷ (9,0 × 10^-6 M/min) = 5,0] lorsque la concentration de cisplatine est augmentée d’un facteur 5 (de 0,0060 M à 0,030 M). La vitesse de la réaction étant directement proportionnelle à la concentration du réactif, l’exposant de la concentration de cisplatine dans la loi de vitesse doit être égal à 1. La loi de vitesse est donc: vitesse = k[cisplatine]¹. La réaction est donc du premier ordre. Sachant cela, nous pouvons calculer la constante de vitesse en utilisant la loi de vitesse différentielle pour une réaction du premier ordre et les données de n’importe quelle ligne du tableau. Par exemple, en substituant les valeurs de l’expérience 3 dans la loi de vitesse différentielle,

3,6 × 10^-5 M/min = k(0,024 M)

1,5 × 10^-3 min^-1 = k

Expérience	[Cisplatine]0 (M)	Vitesse initiale (M/min)
1	0,0060	9,0 × 10−6
2	0,012	1,8 × 10−5
3	0,024	3,6 × 10−5
4	0,030	4,5 × 10−5

La connaissance de la constante de vitesse de l’hydrolyse du cisplatine et des constantes de vitesse des réactions ultérieures qui produisent des espèces hautement toxiques permet aux pharmaciens hospitaliers de fournir aux patients des solutions qui ne contiennent que la forme souhaitée du médicament.

Exemple 7.3.5 – La loi de vitesse intégrée pour une réaction du premier ordre – 1

Si un échantillon de chlorure d’éthyle d’une concentration initiale de 0,0200 M est chauffé à 650°C, quelle est la concentration de chlorure d’éthyle après 10 h? Combien d’heures doivent s’écouler à 650°C pour que la concentration diminue jusqu’à 0,0050 M (k = 1,6 × 10^-6 s^-1)?

Solution

La forme exponentielle de la loi de vitesse intégrée pour une réaction du premier ordre est [A] = [A]₀e^−kt.

Après avoir obtenu la concentration initiale de chlorure d’éthyle ([A]₀) et la constante de vitesse k = 1,6 × 10^-6 s^-1, nous pouvons utiliser la loi de vitesse pour calculer la concentration du réactif à un moment donné t. En substituant les valeurs connues dans la loi de vitesse intégrée,

[CH₃CH₂Cl]_{10 h} = [CH₃CH₂Cl]₀e^-kt

= 0.0200 M(e^{-(1.6 x 10^-6 s^- 1) [(10 h)(60 min/h)(60s/min)]})

= 0.0189 M

Nous aurions également pu utiliser la forme logarithmique de la loi de vitesse intégrée:

ln[CH₃CH₂Cl]_{10 h} = ln[CH₃CH₂Cl]₀ – kt

= ln 0.0200 – (1.6 x 10^-6 s^-1 ) [(10 h)(60 min/h)(60s/min)]

[CH₃CH₂Cl]_{10 h} = e^-3.970 M

= 0.0189 M

Pour calculer le temps nécessaire pour atteindre une concentration donnée, nous devons résoudre la loi de vitesse intégrée pour t. L’utilisation de la loi de vitesse intégrée donne ce qui suit:

ln[CH₃CH₂Cl]_t = ln[CH₃CH₂Cl]₀ – kt

kt = ln[CH₃CH₂Cl]₀ – ln[CH₃CH₂Cl]_t = ln[CH3CH2Cl]0[CH3CH2Cl]t

t = 1k(ln[CH₃CH₂Cl]₀[CH3CH2Cl]_t) = 11.6×10^-6s^-1 (ln0.0200 M 0.0050 M) = 8.7 x 10⁵ s = 240h = 2.4×10²h

Vérifiez votre apprentissage 7.3.6 – La loi de vitesse intégrée pour une réaction du premier ordre – 1

Vous constatez que la décomposition du chlorure de sulfuryle (SO₂Cl₂) est du premier ordre et vous calculez que la constante de vitesse à 320°C est de 2,2 × 10^-5 s^-1. Utilisez la ou les formes de la loi de vitesse intégrée pour trouver la quantité de SO₂Cl₂ qui reste après 20 h si un échantillon ayant une concentration initiale de 0,123 M est chauffé à 320°C. L’équation pour la décomposition de SO₂Cl₂ est:

SO₂Cl₂ (g)   →   SO₂ (g) + Cl₂ (g)

Combien de temps faut-il pour que 90% du SO₂Cl₂ se décompose?

Réponse

0,0252 M; 29 h

Exemple 7.3.6 – La loi de vitesse intégrée pour une réaction du premier ordre – 2

La constante de vitesse pour la décomposition du premier ordre du cyclobutane, C₄H₈ à 500°C est de 9,2 × 10^-3 s^-1:

C₄H₈  →  2C₂H₄

Combien de temps faut-il pour que 80,0% d’un échantillon de C₄H₈ se décompose?

Solution

Nous utilisons la forme intégrée de la loi des vitesses pour répondre aux questions concernant le temps:

ln ([A]0[A]) = kt

Il y a quatre variables dans la loi de vitesse, donc si nous connaissons trois d’entre elles, nous pouvons déterminer la quatrième. Dans ce cas, nous connaissons [A]₀, [A] et k, et nous devons trouver t.

La concentration initiale de C₄H₈, [A]₀, n’est pas indiquée, mais le fait que 80,0% de l’échantillon se soit décomposé est une information suffisante pour résoudre ce problème. Soit x la concentration initiale, auquel cas la concentration après décomposition à 80,0% est de 20,0% de x ou 0,200x. En réarrangeant la loi de vitesse pour isoler t et en substituant les quantités fournies, on obtient:

t=ln|x||0.200x|x1k = ln0.100 molL – 10.020 molL – 1 x 19.2 x 10^-3s^-1 = ln1.609 x 19.2 x 10^-3s^-1 = ln1.7 x 10²s

Vérifiez votre apprentissage 7.3.7

L’iode–131 est un isotope radioactif qui est utilisé pour diagnostiquer et traiter certaines formes de cancer de la thyroïde. L’iode–131 se désintègre en xénon–131 selon l’équation suivante:

I-131 → Xe-131 + électron

La désintégration est du premier ordre avec une constante de vitesse de 0,138 d^-1. Toute désintégration radioactive est du premier ordre. Combien de jours faudra-t-il pour que 90% de l’iode–131 d’une solution 0,500 M de cette substance se désintègre en Xe–131?

Réponse

16,7 jours

Exemple 7.3.7 – Détermination de l’ordre de réaction par graphique

Montrez que les données ci-dessous peuvent être représentées par une loi de vitesse du premier ordre en traçant le graphique de ln [H₂O₂] en fonction du temps. Déterminez la constante de vitesse pour la vitesse de décomposition de H₂O₂ à partir de ces données.

Temps (h)	[H2O2] (mol L-1)	Δ[H2O2] (mol L-1)	Δt (h)	Vitesse de décomposition (mol/L/h)
0,00	1,000	-0,500	6,00	0,0833
6,00	0,500	-0,500 ↔ -0,250	6,00	0,0833 ↔ 0,0417
12,00	0,250	-0,250 ↔ -0,125	6,00	0,0417 ↔ 0,0208
18,00	0,125	-0,125 ↔ -0,062	6,00	0,0208 ↔ 0,0103
24,00	0,0625	-0,062	6,00	0,0103

Solution

Les données ci-dessus avec les valeurs de ln[H₂O₂] sont données dans la Figure 7.3.6.

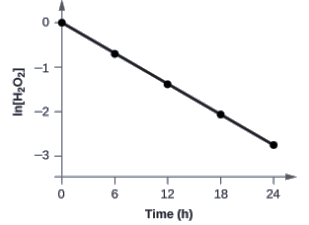
Figure 7.3.6. La relation linéaire entre le ln[H₂O₂] et le temps montre que la décomposition du peroxyde d’hydrogène est une réaction du premier ordre. 

Essai	Temps (h)	[H2O2] (M)	ln[H2O2]
1	0,00	1,000	0,0
2	6,00	0,500	-0,693
3	12,00	0,250	-1,386
4	18,00	0,125	-2,079
5	24,00	0,0625	-2,772

Le graphique de ln[H₂O₂] en fonction du temps est linéaire, nous avons donc vérifié que la réaction peut être décrite par une loi de vitesse du premier ordre.

La constante de vitesse d’une réaction du premier ordre est égale à la valeur négative de la pente de la courbe ln[H₂O₂] en fonction du temps où:

Afin de déterminer la pente de la courbe, nous avons besoin de deux valeurs de ln[H₂O₂] à différentes valeurs de t (il est préférable d’en avoir une près de chaque extrémité de la courbe). Par exemple, la valeur de ln[H₂O₂] lorsque t est de 6,00 h est de -0,693; la valeur lorsque t = 12,00 h est de -1,386:

Vérifiez votre apprentissage 7.3.8 – Détermination de l’ordre de réaction par graphique

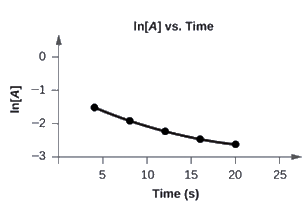
Tracez le graphique des données suivantes pour déterminer si la réaction A → B + C est du premier ordre.

Essai	Temps (s)	[A] (M)
1	4,0	0,220
2	8,0	0,144
3	12,0	0,110
4	16,0	0,088
5	20,0	0,074

Réponse

Le graphique de ln[A] en fonction de t n’est pas une ligne droite. L’équation n’est pas du premier ordre:

La demi-vie des réactions du premier ordre

Nous pouvons dériver une équation pour déterminer la demi-vie d’une réaction du premier ordre à partir de la forme alternative de la loi de vitesse intégrée comme suit:

Si nous fixons le temps t égal à la demi-vie, t_1/2, la concentration correspondante de A à ce moment est égale à la moitié de sa concentration initiale.

Par conséquent, lorsque t = t_1/2, [A] =  12[A]₀.

Par conséquent,

t_1/2 = ln[A]₀12[A]]₀ x 1k = ln2 x 1k = 0.693 x 1k

Ainsi:

t_1/2 = 0.693k

On constate que la demi-vie d’une réaction du premier ordre est inversement proportionnel à la constante de vitesse k et totalement indépendante de la concentration. Une réaction rapide (demi-vie plus courte) aura un k plus grand; une réaction lente (demi-vie plus longue) aura un k plus petit.

Exemple 7.3.8 – Calcul d’une constante de vitesse du premier ordre à l’aide de la demi-vie

Calculez la constante de vitesse pour la décomposition du premier ordre du peroxyde d’hydrogène dans l’eau à 40°C, en utilisant les données de la Figure 7.3.7.

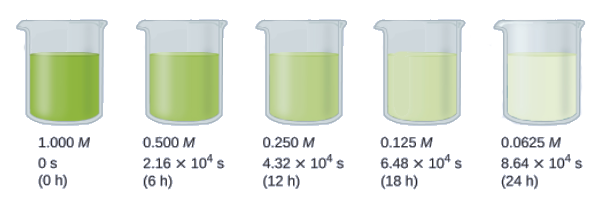
Figure 7.3.7. La décomposition de H₂O₂ (2H₂O₂ → 2H₂O + O₂) à 40°C est illustrée. L’intensité de la couleur symbolise la concentration de H₂O₂ aux moments indiqués; H₂O₂ est en fait incolore. 

Solution

La demi-vie de la décomposition de H₂O₂ est de 2,16 × 10⁴ s:

Vérifiez votre apprentissage 7.3.9 – Calcul d’une constante de vitesse du premier ordre à l’aide de la demi-vie

La désintégration radioactive du premier ordre de l’iode-131 présente une constante de vitesse de 0,138 d^-1. Quelle est la demi-vie de cette désintégration?

Réponse

5,02 d.

Réactions du second ordre

Le type le plus simple de réaction du second ordre est celui dont la vitesse est proportionnelle au carré de la concentration d’un réactif. Elles ont généralement la forme 2A → produits. Un deuxième type de réaction du second ordre a une vitesse de réaction qui est proportionnelle au produit des concentrations de deux réactifs. Ces réactions ont généralement la forme A + B → produits. Un exemple du premier type est une réaction de dimérisation, dans laquelle deux molécules plus petites, chacune appelée monomère, se combinent pour former une molécule plus grande (un dimère).

La loi de vitesse différentielle pour la réaction du second ordre la plus simple dans laquelle 2A → produits est la suivante:

vitesse = -Δ[A]²Δt = k[A]²

Équation 7.3.4 Loi de vitesse différentielle du second ordre

Par conséquent, le fait de doubler la concentration de A quadruple la vitesse de réaction. Pour que les unités de la vitesse de réaction soient des moles par litre par seconde (M/s), les unités d’une constante de vitesse du second ordre doivent être l’inverse (M^-1-s^-1). Comme les unités de molarité sont exprimées en mol/L, l’unité de la constante de vitesse peut également être écrite sous la forme L(mol·s).

Pour la réaction 2A → produits, la loi de vitesse intégrée suivante décrit la concentration du réactif à un instant donné:

1[A] = 1[A]₀ + kt

Cette équation ayant la forme d’une équation algébrique pour une ligne droite, y = mx + b, avec y = 1/[A] et b = 1/[A]₀, le tracé de 1/[A] en fonction de t pour une réaction simple du second ordre est une ligne droite avec une pente de k et un point d’interception de 1/[A]₀.

Les réactions simples du second ordre sont courantes. Outre les réactions de dimérisation, deux autres exemples sont la décomposition de NO₂ en NO et O₂ et la décomposition de HI en I₂ et H₂. La plupart des exemples concernent des molécules inorganiques simples, mais il existe également des exemples organiques. Nous pouvons suivre l’évolution de la réaction décrite dans le paragraphe suivant en surveillant la diminution de l’intensité de la couleur rouge du mélange réactionnel.

De nombreux composés organiques cycliques qui contiennent deux doubles liaisons carbone-carbone subissent une réaction de dimérisation pour donner des structures complexes. Un exemple est le suivant:

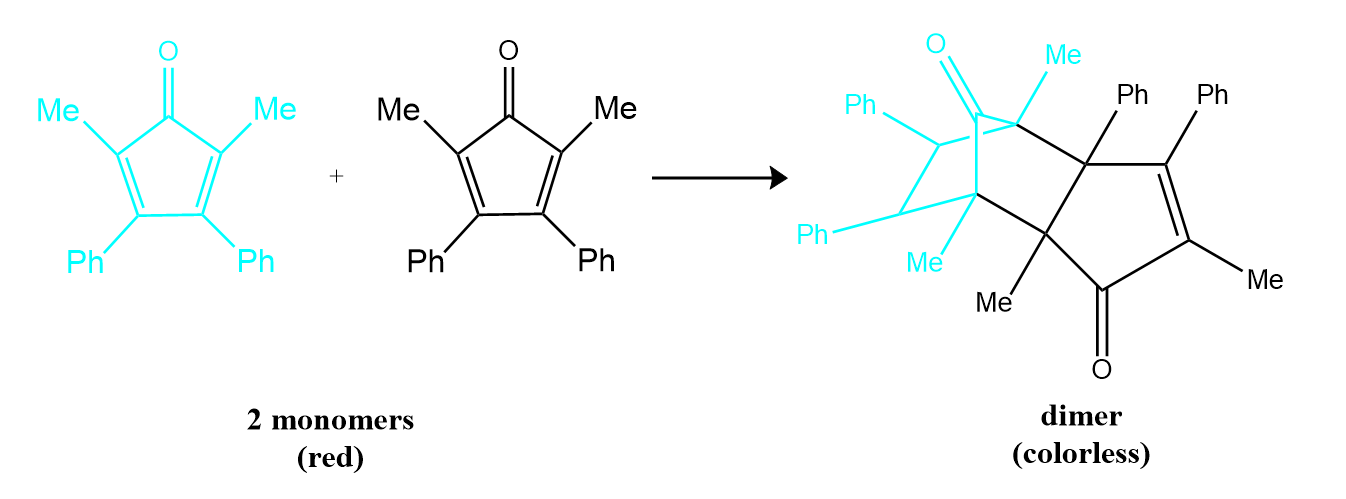
Pour simplifier, nous appellerons ce réactif et ce produit respectivement “monomère” et “dimère”. Le nom systématique du monomère est 2,5-diméthyl-3,4-diphénylcyclopentadiénone. Le nom systématique du dimère est le nom du monomère suivi de “dimère”. Comme les monomères sont les mêmes, l’équation générale de cette réaction est 2A → produit. Cette réaction représente une classe importante de réactions organiques utilisées dans l’industrie pharmaceutique pour préparer des squelettes carbonés complexes pour la synthèse de médicaments. Comme les réactions du premier ordre étudiées précédemment, elle peut être analysée à l’aide de la loi de vitesse différentielle ou de la loi de vitesse intégrée.

Temps (min)	[Monomère] (M)	Vitesse instantanée (M/min)
10	0,0044	8,0 × 10−5
26	0,0034	5,0 × 10−5
44	0,0027	3,1 × 10−5
70	0,0020	1,8 × 10−5
120	0,0014	8,0 × 10−6

Tableau 7.3.3 Temps, vitesse et concentration

Pour déterminer la loi de vitesse différentielle de la réaction, nous avons besoin de données sur la variation de la vitesse de réaction en fonction de la concentration en monomères, qui sont fournies dans le tableau ci-dessus. D’après ces données, nous constatons que la vitesse de réaction n’est pas indépendante de la concentration en monomères, il ne s’agit donc pas d’une réaction d’ordre zéro. Nous constatons également que la vitesse de réaction n’est pas proportionnelle à la concentration en monomères, la réaction n’est donc pas du premier ordre. En comparant les données des deuxièmes et quatrièmes lignes, on constate que la vitesse de réaction diminue d’un facteur 2,8 lorsque la concentration en monomères diminue d’un facteur 1,7:

et

Comme (1,7)² = 2,9 ≈ 2,8, la vitesse de réaction est approximativement proportionnelle au carré de la concentration en monomères.

vitesse ∝ [monomère]²

Cela signifie que la réaction est du second ordre dans le monomère. En utilisant la loi de vitesse différentielle et les données de n’importe quelle ligne du tableau, nous pouvons calculer la constante de vitesse. En substituant les valeurs au temps 10 min, par exemple, on obtient ce qui suit:

vitesse = k[A]²

Nous pouvons également déterminer l’ordre de la réaction à l’aide de la loi de vitesse intégrée. Pour ce faire, nous utilisons la diminution de la concentration du monomère en fonction du temps pour une seule réaction, représentée dans la partie (a) de la Figure 7.3.8. Les mesures montrent que la concentration du monomère (initialement 5,4 × 10^-3 M) diminue avec l’augmentation du temps. Ce graphique montre également que la vitesse de réaction diminue de façon régulière avec l’augmentation du temps. Selon la loi de vitesse intégrée pour une réaction du second ordre, le tracé de 1/[monomère] en fonction de t devrait être une ligne droite, comme le montre la partie (b) de la Figure 7.3.8. Toute paire de points sur la ligne peut être utilisée pour calculer la pente, qui est la constante de vitesse du second ordre. Dans cet exemple, k = 4,1 M^-1·min⁻¹, ce qui est cohérent avec le résultat obtenu à l’aide de l’équation différentielle de vitesse. Bien que dans cet exemple le coefficient stœchiométrique soit le même que l’ordre de réaction, ce n’est pas toujours le cas. L’ordre de réaction doit toujours être déterminé expérimentalement.

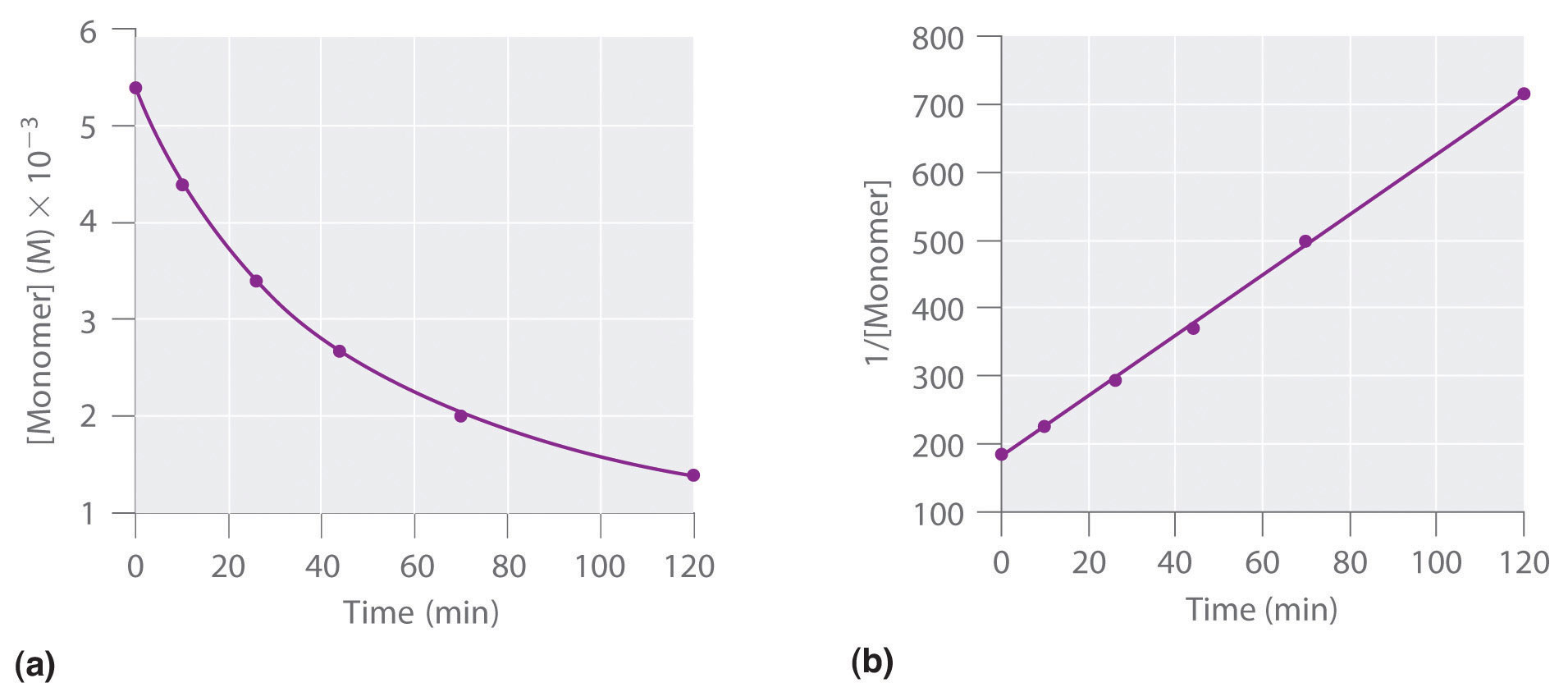
Figure 7.3.8. Ces graphiques correspondent à la dimérisation du monomère comme (a) la concentration de monomère déterminée expérimentalement en fonction du temps et (b) 1/[monomère] en fonction du temps. La ligne droite en (b) est attendue pour une réaction simple du second ordre.

Pour deux ou plusieurs réactions du même ordre, la réaction dont la constante de vitesse est la plus grande est la plus rapide. Cependant, comme les unités des constantes de vitesse pour les réactions d’ordre zéro, du premier et du second ordre sont différentes, nous ne pouvons pas comparer l’ampleur des constantes de vitesse pour des réactions d’ordres différents.

En plus de la réaction simple du second ordre et de la loi de vitesse que nous venons de décrire, une autre réaction du second ordre très courante a la forme générale A + B → produits, dans laquelle la réaction est du premier ordre en A et du premier ordre en B. La loi de vitesse différentielle pour cette réaction est la suivante:

vitesse = -Δ[A]Δt = -Δ[B]Δt = k[A][B]

Comme la réaction est du premier ordre à la fois en A et en B, elle a un ordre de réaction global de 2. (La loi de vitesse intégrée pour cette réaction est plutôt complexe, nous ne la décrirons donc pas). Nous pouvons reconnaître les réactions du second ordre de ce type car la vitesse de réaction est proportionnelle aux concentrations de chaque réactif.

Exemple 7.3.9 – La loi de vitesse intégrée pour une réaction du second ordre – 1

La réaction du gaz butadiène (C₄H₆₎ avec lui-même produit du gaz C₈H₁₂ comme suit:

2C₄H₆ (g)  →  C₈H₁₂ (g)

La réaction est du second ordre avec une constante de vitesse égale à 5,76 × 10^-2 L/mol/min dans certaines conditions. Si la concentration initiale de butadiène est de 0,200 M, quelle est la concentration restante après 10,0 min?

Solution

Nous utilisons la forme intégrée de la loi de vitesse pour répondre aux questions concernant le temps. Pour une réaction du second ordre, nous avons:

1[A] = kt + 1[A]₀

Nous connaissons trois variables dans cette équation: [A]₀ = 0,200 mol/L, k = 5,76 × 10^-2 L/mol/min, et t = 10,0 min. Par conséquent, nous pouvons résoudre [A], la quatrième variable:

Par conséquent, il reste 0,179 mol/L de butadiène à la fin de 10,0 min, par rapport aux 0,200 mol/L qui étaient initialement présents.

Vérifiez votre apprentissage 7.3.10 – La loi de vitesse intégrée pour une réaction du second ordre – 1

Si la concentration initiale de butadiène est de 0,0200 M, quelle est la concentration restante après 20,0 min?

Réponse

0,0195 mol/L

Exemple 7.3.10 – La loi de vitesse intégrée pour une réaction du second ordre – 2

À haute température, le dioxyde d’azote se décompose en oxyde nitrique et en oxygène.

2NO₂ (g)  →  2NO (g) + O₂ (g)

Si une fiole qui contient initialement 0,056 M de NO₂ est chauffé à 300°C, quelle sera la concentration de NO₂ après 1,0 h? Combien de temps faudra-t-il pour que la concentration de NO₂ diminue jusqu’à 10% de la concentration initiale? Utilisez la loi de vitesse intégrée pour une réaction du second ordre et la constante de vitesse k = 0,54 M^-1·s^-1.

Solution

Nous connaissons k et [NO₂]₀, et on nous demande de déterminer [NO₂] à t = 1 h (3600 s). En substituant les valeurs appropriées,

Dans ce cas, nous connaissons k et [NO₂]₀, et on nous demande de calculer à quel moment [NO₂] = 0,1[NO₂]₀ = 0,1(0,056 M) = 0,0056 M. Pour ce faire, nous résolvons la loi de vitesse intégrée pour t, en utilisant les concentrations données.

t = (1/[NO₂]) – (1/[NO₂]⁰)k = (1/0.0056M) – (1/0.056M)0.54M-1・s^-1 = 3.0×10² s = 5.0minutes

Le NO₂ se décompose très rapidement; dans ces conditions, la réaction est complète à 90% en seulement 5,0 min.

Vérifiez votre apprentissage 7.3.11 – La loi de vitesse intégrée pour une réaction du second ordre – 2

Lorsque l’espèce hautement réactive HO₂ se forme dans l’atmosphère, une importante réaction du second ordre qui l’élimine ensuite de l’atmosphère est la suivante:

2HO₂ (g)  →  H₂O₂ (g) + O₂ (g)

Vous calculez la constante de vitesse pour la décomposition de HO₂ comme étant k = 1,4 × 10⁹ M^-1-s^-1. Cette constante de vitesse élevée signifie que le HO₂ se décompose rapidement dans les conditions de réaction données dans le problème. En fait, la molécule de HO₂ est tellement réactive qu’il est pratiquement impossible de l’obtenir à des concentrations élevées. Étant donné un échantillon de 0,0010 M de HO₂, calculez la concentration de HO₂ qui reste après 1,0 h à 25°C. Combien de temps faudra-t-il pour que 90% du HO₂ se décompose? Utilisez la loi de vitesse intégrée pour une réaction du second ordre et la constante de vitesse k = 1,4 × 10⁹ M^-1ᐧs^-1.

Réponse

2,0 × 10^-13 M; 6,4 × 10^-6 s

Exemple 7.3.11 – Détermination de l’ordre de réaction à l’aide d’un graphique

Les données ci-dessous concernent la même réaction que celle décrite dans l’exemple “La loi de vitesse intégrée pour une réaction du second ordre – 1″. Testez ces données pour confirmer que cette réaction de dimérisation est du second ordre.

Solution

Essai	Temps (s)	[C4H6] (M)
1	0	1,00 × 10−2
2	1600	5,04 × 10−3
3	3200	3,37 × 10−3
4	4800	2,53 × 10−3
5	6200	2,08 × 10−3

 

Afin de distinguer une réaction du premier ordre d’une réaction du second ordre, nous traçons le graphique ln [C₄H₆] en fonction de t et le comparons à un graphique de

en fonction de t. Les valeurs nécessaires pour ces tracés sont les suivantes.

Temps (s)	1[C4H6] (M-1)	ln [C4H6]
0	100	-4,605
1600	198	-5,289
3200	296	-5,692
4800	395	-5,978
6200	481	-6,175

Les courbes sont présentées à la Figure 7.3.9. Comme vous pouvez le constater, le graphique de ln [C₄H₆] en fonction de t n’est pas linéaire, la réaction n’est donc pas du premier ordre. Le graphique de 1[C4H6] en fonction de t est linéaire, ce qui indique que la réaction est du second ordre.

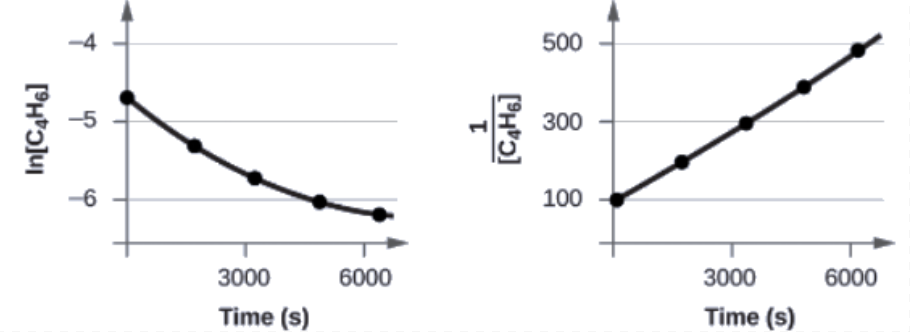
Figure 7.3.9. Ces deux graphiques montrent les courbes du premier et du second ordre pour la dimérisation de C₄H₆. Comme le tracé du premier ordre (à gauche) n’est pas linéaire, nous savons que la réaction n’est pas du premier ordre. La tendance linéaire du graphique du second ordre (à droite) indique que la réaction suit une cinétique du second ordre.

Vérifiez votre apprentissage 7.3.12 – Détermination de l’ordre de réaction à l’aide d’un graphique

Les données suivantes correspondent-elles à une loi de vitesse d’ordre 2?

Essai	Temps (s)	[A] (M)
1	5	0,952
2	10	0,625
3	15	0,465
4	20	0,370
5	25	0,308
6	35	0,230

Réponse

Oui. Le graphique de 1[A] en fonction de t est linéaire:

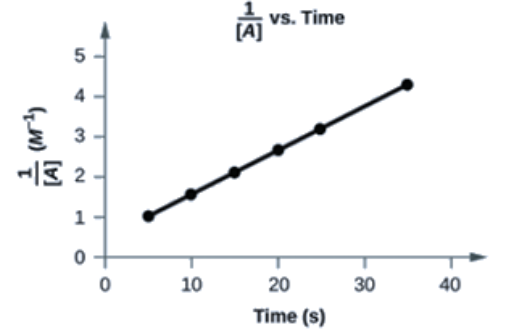
Demi-vie des réactions du second ordre

Nous pouvons dériver l’équation pour calculer la demi-vie d’un second ordre comme suit:

1[A] = kt+1[A]₀

ou

1[A] – 1[A]₀ = kt

Si

t = t_1/2

puis

[A] = 12[A]₀

et nous pouvons écrire:

 t_1/2 = 1k[A]₀

Pour une réaction du second ordre, t_1/2 est inversement proportionnel à la concentration du réactif (sa demi-vie dépend donc de la concentration), et la demi-vie augmente au fur et à mesure que la réaction se déroule car la concentration du réactif diminue. Par conséquent, l’utilisation du concept de demi-vie est plus complexe pour les réactions du second ordre que pour les réactions du premier ordre. Contrairement aux réactions du premier ordre, la constante de vitesse d’une réaction du second ordre ne peut pas être calculée directement à partir de la demi-vie, à moins que la concentration initiale ne soit connue.

Questions

★ Questions

Notez: Rappelons que les unités utilisées dans les équations de loi de vitesses seront différentes les unes des autres en fonction de leur ordre.

Dans la réaction 4A + 3B  →  2C + 3D, on constate que la réaction A disparaît à une vitesse de 5,1 X 10^-5 Ms^-1.

Quelle est la vitesse de la réaction?

Quelle est la vitesse de disparition de B?

Quelle est la vitesse de formation du C?

Dans la réaction 3A + 2B  →  C + 2D, on constate que la réaction A disparaît à une vitesse de 4,6 x 10^-5 Ms^-1.

Quelle est la vitesse de la réaction?

Quelle est la vitesse de disparition du réactif B?

Quel est la vitesse d’apparition du produit D?

Dans la réaction A  →  B, on constate que [A] est de 0,750 M à t = 61,2s et de 0,704 M à t = 73,5s. Déterminer la vitesse moyenne de la réaction pendant cet intervalle de temps.

Quelle est la vitesse moyenne de réaction sur un intervalle de temps pour [A] si elle est de 0,455 M à t = 80,25s et de 0,474 M à t = 82,4s?

Pour la réaction A + 2B  →  2C, la vitesse de réaction est de 1,75 x 10^-5 Ms^-1 au moment où [A] = 0,3575 M.

Quelle est la vitesse de formation du C?

Quelle sera la valeur de [A] 1 minute plus tard?

Supposons que la vitesse reste à 1,75 x 10^-5 Ms^-1. Combien de temps faut-il pour que [A] passe de 0,3580 à 0,3500 M?

On détermine la vitesse initiale de la réaction A + B  →  C + D pour différentes conditions initiales, les résultats étant répertoriés dans le tableau.

Expt[A]	M[B]	MVitesse Initiale M s-1
10.185	0.144	3.35 x 10-4
20.185	0.288	1.35 x 10-3
30.370	0.144	6.75 x 10-4
40.370	0.288	2.70 x 10-3

Quel est l’ordre de la réaction par rapport à A et à B?

Quel est l’ordre global de la réaction?

Quelle est la valeur de la constante de vitesse, k?

On détermine la vitesse initiale de la réaction A + B  →  C + D pour différentes conditions initiales, les résultats étant répertoriés dans le tableau :

Expt[A]	M[B]	MInitial Rate M s-1
10.331	0.203	2.205 x 10-4
20.331	0.406	8.82 x 10-4
30.662	0.203	4.41 x 10-4
40.662	0.406	1.7 x 10-3

Quel est l’ordre de la réaction par rapport à A et B ?

Quel est l’ordre global de la réaction ?

Quelle est la valeur de la constante de vitesse k ?

On détermine la vitesse initiale de la réaction A + B  →  C + D pour des conditions initiales différentes, les résultats étant répertoriés dans le tableau:

Expt[A]	M[B]	MInitial Rate M s-1
10.241	0.153	1.261 x 10-4
20.241	0.306	5.044 x 10-4
30.482	0.153	2.522 x 10-4
40.482	0.306	6.741 x 10-4

Quel est l’ordre de la réaction par rapport à A et B? Écrivez les lois de vitesse respectives pour A et B

Quel est l’ordre global de la réaction?

Quelle est la valeur de k, la constante de vitesse?

La réaction du premier ordre A→produits a t_1/2 = 300s.

Quel pourcentage de l’échantillon A reste non réagi 1000 s après le début de la réaction?

Quelle est la vitesse de réaction lorsque [A] = 0,25M?

 

Une réaction du premier ordre A→produits a une demi-vie de 120 secondes, calculer le suivant:

Quel pourcentage de A reste non réagi après 800 secondes de réaction?

Quelle est la vitesse de la réaction à [A] = 0,25M?

 

La réaction du premier ordre a un t_1/2 de 250s.

Quel pourcentage d’un échantillon de A reste non réagi 1500s après le début d’une réaction?

Et si la vitesse de la réaction est égale à la moitié de la vitesse de disparition de A?

★★ Questions

La réaction A→produits est du premier ordre en A

Si 4,2g de A se décompose pendant 45 minutes, on mesure que le A non décomposé est de 1,05g. Quelle est la demi-vie, t_1/2, de cette réaction (en minutes)?

En partant des mêmes 4,2 g, quelle est la masse (en grammes) de A non décomposé après 75 minutes?

Expliquez pourquoi

Une vitesse de réaction ne peut pas être calculée à partir de la seule fréquence de collision.

La vitesse d’une réaction chimique peut augmenter de façon spectaculaire avec la température, alors que la fréquence des collisions augmente beaucoup plus lentement.

L’introduction d’un catalyseur dans un mélange réactionnel peut avoir un impact considérable sur la vitesse de la réaction, même si la température est maintenue constante.

Répondez aux questions suivantes:

La vitesse de réaction dépend sur quels deux facteurs, autre que la fréquence des collisions?

Pourquoi la vitesse de réaction augmente-t-elle considérablement avec la température?

Quel est l’effet net de l’ajout d’un catalyseur?

Réponses

Vitesse de disparition de B = vitesse de réaction X coefficient de B

(1.3 x 10^-5 M s^-1)(3) = 3.9×10^-5 M s^-1

Vitesse de formation de C = taux de réaction X coefficient de C

(1.3 x 10^-5 M s^-1)(2) = 2.6×10^-5 M s^-1

Vitesse de disparition de B = (vitesse de la réaction) X 2(coefficient de B)

(1.5 x 10^-5 M s^-1)(2) = 3.1×10^-5 M s^-1

Même procédé que B) (multiplier la vitesse de réaction par 2) OU:

Vitesse d’apparition de D = -13(2)(Δ[A]Δt) = -23(4.6×10^-5 M s^-1) = 3.1×10^-5 M s^-1

Vitesse de disparition de B = vitesse de réaction X coefficient de B

(1.3 x 10^-5 M s^-1)(3) = 3.9×10^-5 M s^-1

Vitesse de formation de C = vitesse de réaction X coefficient de C

(1.3 x 10^-5 M s^-1)(2) = 2.6×10^-5 M s^-1

(a) Ordre par rapport à A = 1, Ordre par rapport à B = 2; (b) ordre global de la réaction = 3; (c) 0,103 M s^-1

Ordre de la réaction par rapport à B:

Trouver où A est constant et B change (Réaction 1 et Réaction 2)

Diviser : Réaction2 / Réaction1 = 8.82×10^-4 2.205×10^-4 = [0.331]^m[0.406]ⁿ[0.331]^m[0.203]ⁿ

La réaction est donc du second ordre par rapport à B.

Ordre de la réaction par rapport à A:

Trouver où B est constant et A change (Réaction 1 et Réaction 2)

Diviser : Réaction3 / Réaction1 = 4.41×10^-4 2.205×10^-4 = [0.406]^m[0.662]ⁿ[0.203]^m[0.662]ⁿ

Réaction3 / Réaction1 = 2 = 2m → m = 1

La réaction est donc du second ordre par rapport à A

b) Ordre de réaction = ordre de réaction de A + ordre de réaction de B = 3ième ordre de réaction

c) 2.205 x 10^-4 = k x [0.331][0.203]2k = 1.6 x 10^-2

La réaction est du premier ordre par rapport à A

Ordre de réaction global = (ordre de réaction de A + ordre de réaction de B) = 1 + 2 = 3e ordre global

k = 0.0224 M^-2s^-1

ln(%nonréagi) = -kt

k = ln2 t_1/2 = ln2300 s = 0.0023 s^-1

ln(%nonréagi) = -(0.0023 ^s-1)(1000 s) = -2.3

Vitesse = k[A]

Vitesse = 0.0023 s^-1

[0.25 M] = 5.74 x 10^-4 M s^-1

t_1/2 (premier ordre) = ln2k

k = ln2 t_1/2 = ln2 120 s = 5.77×10^-3

pourcentage de non-réaction défini par [A]_t[A]₀

Pour une réaction du premier ordre, la vitesse = k[C] = 0.0046/s x 0.25 = 1.15 x 10^-3 M/s

k = ln2 t_1/2 = 0.693250s = 0.00277s-1

ln(%nonréagi) = -kt = (-.00277 s^-1)(1500 s) = -4.155

%nonréagi = 0.0157 x 100% = 1.57% de la quantité initiale

Vitesse = k[A] = (0.00277 s^-1)(0.5 M) = 0.00139 M/s

(4.2 g)(14) = 1.05 g → 2 demi-vies sont passées → 45minutes / 2 = t_1/2 = 22.5 minutes

k = ln2 t_1/2 = ln2 22.5minutes = 0.0308 min^-1