6.4 – Équilibres des composés ioniques légèrement solubles
Solubilité
Lorsqu’une substance solide est mélangée à un solvant afin de former une solution, il y a plusieurs résultats possibles. Le facteur déterminant pour le résultat est la solubilité de la substance, qui est définie comme la concentration maximale possible du soluté. Les règles de solubilité permettent de déterminer quelles substances sont solubles et dans quelle mesure.
Effets de la solubilité sur les réactions
En fonction de la solubilité d’un soluté, il y a trois résultats possibles : 1) si la solution contient moins de soluté que la quantité maximale qu’elle est capable de dissoudre (sa solubilité), il s’agit d’une solution insaturée diluée ; 2) si la quantité de soluté est exactement la même que sa solubilité, elle est saturée ; 3) s’il y a plus de soluté que ce qui peut être dissous, il est dit sursaturé et l’excès de soluté se sépare de la solution. Si ce processus de séparation comprend une cristallisation, il forme un précipité. La précipitation abaisse la concentration du soluté jusqu’à la saturation afin d’augmenter la stabilité de la solution.
Nous pouvons utiliser les règles générales suivantes pour prédire la solubilité relative de nombreux composés ioniques :
Règles de solubilité
Les sels contenant des éléments du groupe I (Li+, Na+, K+, Cs+, Rb+) sont solubles. Il y a peu d’exceptions à cette règle. Les sels contenant l’ion ammonium (NH4+) sont également solubles.
Les sels contenant des ions nitrate (NO3–) sont généralement solubles.
Les sels contenant Cl–, Br–, ou I– sont généralement solubles. Les sels halogénures de Ag+, Pb2+ et Hg22+ constituent des exceptions importantes à cette règle. Ainsi, AgCl, PbBr2 et Hg2Cl2 sont insolubles.
La plupart des sels d’argent sont insolubles. AgNO3 et Ag(C2H3O2) sont des sels d’argent solubles courants ; pratiquement tous les autres sont insolubles.
La plupart des sels de sulfate sont solubles. Parmi les exceptions importantes à cette règle figurent le CaSO4, BaSO4, PbSO4, Ag2SO4 et SrSO4 .
La plupart des sels d’hydroxyde ne sont que légèrement solubles. Les sels d’hydroxyde des éléments du groupe I sont solubles. Les sels d’hydroxyde des éléments du groupe II (Ca, Sr et Ba) sont légèrement solubles. Les sels d’hydroxyde des métaux de transition et de Al3+ sont insolubles. Ainsi, Fe(OH)3, Al(OH)3, Co(OH)2 ne sont pas solubles.
La plupart des sulfures de métaux de transition sont très insolubles, notamment le CdS, le FeS, le ZnS et l’Ag2S. Les sulfures d’arsenic, d’antimoine, de bismuth et de plomb sont également insolubles.
Les carbonates sont souvent insolubles. Les carbonates du groupe II (CaCO3, SrCO3 et BaCO3) sont insolubles, tout comme le FeCO3 et le PbCO3.
Les chromates sont souvent insolubles. Citons par exemple le PbCrO4 et le BaCrO4.
Les phosphates tels que Ca3(PO4)2 et Ag3PO4 sont souvent insolubles.
Les fluorures tels que le BaF2, le MgF2 et le PbF2 sont souvent insolubles.
Exemple 6.4.1 – Règles de solubilité
Prévoir le résultat du mélange de solutions raisonnablement concentrées des composés ioniques suivants. Si une précipitation est prévue, écrivez une équation ionique nette équilibrée pour la réaction.
Le sulfate de potassium et le nitrate de baryum
Chlorure de lithium et acétate d’argent
Le nitrate de plomb et le carbonate d’ammonium
Solution
Les deux produits possibles pour cette combinaison sont KNO3 et BaSO4. Les directives de solubilité indiquent que BaSO4 est insoluble, et donc une réaction de précipitation est attendue. L’équation ionique nette pour cette réaction, dérivée de la manière détaillée dans le module précédent, est la suivante Ba2+ (aq) + SO42- (aq) → BaSO4 (s)
Les deux produits possibles pour cette combinaison sont le LiC2H3O2 et l’AgCl. Les directives de solubilité indiquent que l’AgCl est insoluble, et qu’une réaction de précipitation est donc attendue. L’équation ionique nette pour cette réaction, dérivée de la manière détaillée dans le module précédent, est la suivante Ag+ (aq) + Cl– (aq) → AgCl (s)
Les deux produits possibles pour cette combinaison sont la PbCO3 et le NH4NO3. Les directives de solubilité indiquent que la PbCO3 est insoluble, et qu’une réaction de précipitation est donc attendue. L’équation ionique nette pour cette réaction, dérivée de la manière détaillée dans le module précédent, est la suivante Pb2+ (aq) + CO32- (aq) → PbCO3 (s)
Vérifiez votre apprentissage 6.4.1 – Règles de solubilité
Écrivez l’équation ionique de la dissolution et du produit de solubilité pour chacun des composés légèrement solubles suivants :
(a) BaSO4
(b) Ag2SO4
(c) Al(OH)3
(d) Pb(OH)Cl
Réponse
BaSO4 (s) ⇌ Ba2+ (aq) + SO42- (aq)
Ag2SO4 (s) ⇌ 2Ag+ (aq) + SO42- (aq)
Al(OH)3 (s) ⇌ Al3+ (aq) + 3OH– (aq)
Pb(OH)Cl (s) ⇌ Pb2+ (aq) + OH– (aq)+ Cl– (aq)
La constante du produit de solubilité
En appliquant les règles de solubilité ci-dessus, nous pouvons faire des prédictions qualitatives sur les réactions de précipitation. Cependant, ces précipités existent toujours en équilibre dynamique avec les ions aqueux, car il s’agit de composés techniquement peu (ou légèrement) solubles qui se dissolvent partiellement dans les solutions aqueuses. Par exemple, selon les règles de solubilité, le chlorure d’argent, AgCl, est classé comme un solide ionique peu soluble (figure 6.4.1). Cependant, lorsque nous ajoutons un excès de AgCl solide à l’eau, il se dissout dans une faible mesure et produit un mélange constitué d’une solution très diluée d’ions Ag+ et Cl– en équilibre avec du chlorure d’argent non dissous :
dissolution
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq)
précipitations
Cet équilibre, comme d’autres équilibres, est dynamique ; une partie du solide AgCl se dissout continuellement, mais en même temps, les ions Ag+ et Cl- dans la solution se combinent pour produire une quantité égale de solide. À l’équilibre, les processus opposés ont des taux égaux et, au niveau macroscopique, les concentrations d’ions dissous et la masse de solide restant semblent constantes.
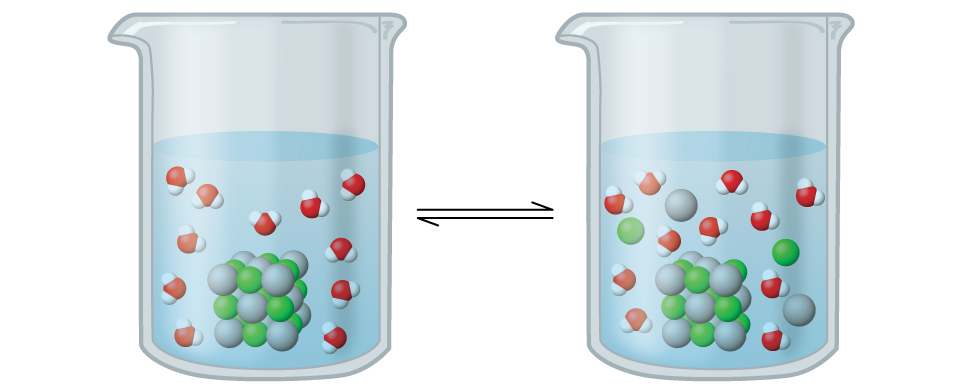
Figure 6.4.1. Le chlorure d’argent est un solide ionique peu soluble. Lorsqu’il est ajouté à l’eau, il se dissout légèrement et produit un mélange constitué d’une solution très diluée d’ions Ag+ et Cl- en équilibre avec du chlorure d’argent non dissous.
La constante d’équilibre pour l’équilibre entre un solide ionique légèrement soluble et une solution de ses ions est le produit de solubilité (Ksp) du solide. Rappelons au chapitre 4 que nous utilisons la concentration d’un ion comme approximation de son activité dans une solution diluée. Pour le chlorure d’argent, à l’équilibre :
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq)
Lorsque l’on examine les réactions de dissolution de ce type, le solide est répertorié comme un réactif, tandis que les ions sont répertoriés comme des produits. La constante de produit de solubilité, comme toute expression de constante d’équilibre, s’écrit comme le produit des concentrations de chacun des ions, portées à la puissance de leurs coefficients stœchiométriques. Ici, la constante du produit de solubilité est égale à [Ag+] x [Cl–] lorsqu’une solution de chlorure d’argent est en équilibre avec de l’AgCl non dissous. Il n’y a pas de dénominateur représentant les réactifs dans cette expression d’équilibre puisque le réactif est un solide pur ; par conséquent, [AgCl] n’apparaît pas dans l’expression pour Ksp.
Certains produits de solubilité courants sont énumérés dans le tableau 6.4.1, en fonction de leur valeur Ksp, tandis qu’une compilation plus complète des produits figure à l’annexe L. Chacune de ces constantes d’équilibre est beaucoup plus petite que 1 parce que les composés énumérés ne sont que légèrement solubles. Un petit Ksp représente un système dans lequel l’équilibre se trouve à gauche, de sorte que relativement peu d’ions hydratés seraient présents dans une solution saturée.
Tableau 6.4.1 Produits de solubilité courants et leurs constantes d’équilibre
|
Substance |
Ksp à 25 °C |
|
CuCl |
1.2 × 10–6 |
|
CuBr |
6.27 × 10–9 |
|
AgI |
1.5 × 10–16 |
|
PbS |
7 × 10–29 |
|
Al(OH)3 |
2 × 10–32 |
|
Fe(OH)3 |
4 × 10–38 |
Exemple 6.4.2 – Rédaction d’équations et de produits de solubilité
Écrire l’équation ionique pour la dissolution et l’expression du produit de solubilité pour chacun des composés ioniques légèrement solubles suivants :
(a) AgI, iodure d’argent, un solide aux propriétés antiseptiques
b) CaCO3, le carbonate de calcium, l’ingrédient actif de nombreux antiacides à mâcher en vente libre
(c) Mg(OH)2, hydroxyde de magnésium, l’ingrédient actif du Lait de magnésie
(d)Mg(NH4)PO4, phosphate d’ammonium et de magnésium, une substance essentiellement insoluble utilisée dans les essais de magnésium
(e) Ca5(PO4)3OH, l’apatite minérale, source de phosphate pour les engrais
(Conseil : pour déterminer comment décomposer les éléments (d) et (e) en ions, reportez-vous à la liste des ions polyatomiques dans la section sur la nomenclature chimique).
Solution
AgI (s) ⇌ Ag+ (aq) + I– (aq)
CaCO3 (aq) ⇌ Ca2+ (aq) + CO32- (aq)
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
Mg(NH4)PO4 (s) ⇌ Mg+ (aq) + NH4+ (aq) + PO43- (aq)
Ca5(PO4)3OH (s) ⇌ 5Ca2+ (aq) + 3PO43- (aq) + OH– (aq)
Vérifiez votre apprentissage 6.4.1 – Rédaction d’équations et de produits de solubilité
Écrivez l’équation ionique de la dissolution et du produit de solubilité pour chacun des composés légèrement solubles suivants :
(a) BaSO4
(b) Ag2SO4
(c) Al(OH)3
(d) Pb(OH)Cl
Réponse
BaSO4 (s) ⇌ Ba2+ (aq) + SO42- (aq)
Ag2SO4 (s) ⇌ 2Ag+ (aq) + SO42- (aq)
Al(OH)3 (s) ⇌ Al3+ (aq) + 3OH– (aq)
Pb(OH)Cl (s) ⇌ Pb2+ (aq) + OH– (aq)+ Cl– (aq)
Nous allons maintenant étendre la discussion sur le Ksp et montrer comment la constante du produit de solubilité est déterminée à partir de la solubilité de ses ions, ainsi que comment le Ksp peut être utilisé pour déterminer la solubilité molaire d’une substance.
Le produit ionique
Le produit ionique (Q) d’un sel est le produit des concentrations des ions en solution portées aux mêmes puissances que dans l’expression du produit de solubilité. Il est analogue au quotient de réaction (Q) discuté pour les équilibres au chapitre 4. Alors que Ksp décrit les concentrations d’équilibre, le produit ionique décrit des concentrations qui ne sont pas nécessairement des concentrations d’équilibre.
Comme le résume la figure 6.4.2, il existe trois conditions possibles pour une solution aqueuse d’un solide ionique :
Q < Ksp. La solution est insaturée, et une plus grande partie du solide ionique, si elle est disponible, se dissout.
Q = Ksp. La solution est saturée et à l’équilibre.
Q > Ksp. La solution est sursaturée, et le solide ionique va précipiter.
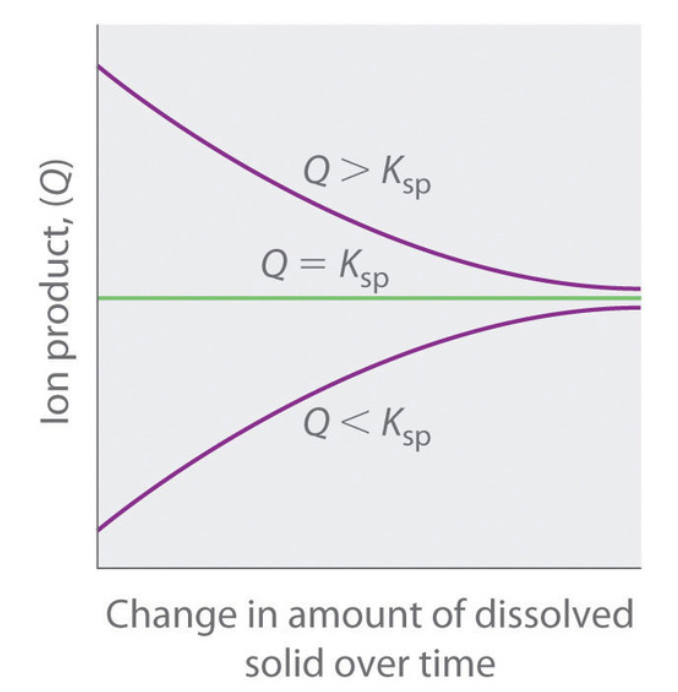
Figure 6.4.2. La relation entre Q et Ksp. Si Q est inférieur à Ksp, la solution est insaturée et plus solide se dissout jusqu’à ce que le système atteigne l’équilibre (Q = Ksp). Si Q est supérieur à Ksp, la solution est sursaturée et le solide précipitera jusqu’à ce que Q = Ksp. Si Q = Ksp, la vitesse de dissolution est égale à la vitesse de précipitation ; la solution est saturée et il n’y a pas de changement net dans la quantité de solide dissous.
Le processus de calcul de la valeur du produit ionique et sa comparaison avec l’ampleur du produit de solubilité est un moyen simple de déterminer si une solution est insaturée, saturée ou sursaturée. Plus important encore, le produit ionique indique aux chimistes si un précipité se formera lorsque des solutions de deux sels solubles sont mélangées.
Ksp et solubilité
Rappelons que la définition de la solubilité est la concentration maximale possible d’un soluté dans une solution à une température et une pression donnée. Nous pouvons déterminer le produit de solubilité d’un solide légèrement soluble à partir de cette mesure de sa solubilité à une température et une pression donnée, à condition que la seule réaction significative qui se produit lorsque le solide se dissout soit sa dissociation en ions solvatés, c’est-à-dire que le seul équilibre impliqué soit :
MpXq (s) ⇌ pMm+ (aq) + qXn- (aq)
Équation 6.4.1. Produit de solubilité d’un solide légèrement soluble
Dans ce cas, nous calculons le produit de solubilité en prenant la solubilité du solide exprimée en unités de moles par litre (mol/L), appelée solubilité molaire.
Exemple 6.4.3 – Calcul du Ksp à partir des concentrations à l’équilibre
La fluorite, CaF2, est un solide légèrement soluble qui se dissout selon l’équation :
CaF2 (s) ⇌ Ca2+ (aq) + 2F– (aq)
La concentration de Ca2+ dans une solution saturée de CaF2 est de 2,15 × 10-4 M ; par conséquent, celle de F– est de 4,30 × 10-4 M, soit deux fois la concentration de Ca2+. Quel est le produit de solubilité de la fluorine ?
Solution
D’abord, écrivez l’expression Ksp, puis substituez-la par des concentrations et résolvez pour Ksp :
CaF2 (s) ⇌ Ca2+ (aq) + 2F– (aq)
Une solution saturée est une solution à l’équilibre avec le solide. Ainsi :
Ksp=[Ca2+][F–]2=(2.1×10-4)(4.2×10-4)2=3.7×10-11
Comme pour les autres constantes d’équilibre, nous n’incluons pas les unités avec Ksp.
Vérifiez votre apprentissage 6.4.2 – Calcul du Ksp à partir des concentrations à l’équilibre
Dans une solution saturée qui est en contact avec du Mg(OH)2 solide, la concentration de Mg2+ est de 1,31 × 10-4 M. Quel est le produit de solubilité du Mg(OH)2 ?
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
Réponse
8.99 × 10–12
Exemple 6.4.4 – Détermination de la solubilité molaire à partir du Ksp
Le Ksp du bromure de cuivre(I), CuBr, est de 6,3 × 10-9. Calculez la solubilité molaire du bromure de cuivre.
Solution
La constante du produit de solubilité du bromure de cuivre(I) est de 6,3 × 10-9.
La réaction est la suivante :
CuBr (s) ⇌ Cu+ (aq) + Br– (aq)
D’abord, écrivez l’expression constante de l’équilibre du produit de solubilité :
Ksp=[Cu+][Br–]
Créez un tableau ICE (comme présenté au chapitre 4), en laissant la colonne CuBr vide car il s’agit d’un solide (son activité est égale à un) et n’apparaît donc pas dans l’expression Ksp :
CuBr ⇌ Cu+ + Br–
|
Concentration initiale (M) |
|
0 |
0 |
|
Changement (M) |
|
x |
x |
|
Concentration d’équilibre (M) |
|
0 + x = x |
0 + x = x |
A l’équilibre :
Ksp=[Cu+][Br–]
6.3×10-9=(x)(x)=x2
x=(6.3×10-9)=7.9×10-5
Par conséquent, la solubilité molaire du CuBr est de 7,9 × 10-5 M.
Vérifiez votre apprentissage 6.4.3 – Détermination de la solubilité molaire à partir du Ksp
Le Ksp de l’AgI est de 1,5 × 10-16. Calculer la solubilité molaire de l’iodure d’argent.
Réponse
1.2 × 10–8 M
Exemple 6.4.5 – Détermination de la solubilité molaire à partir du Ksp, Partie II
Le Ksp de l’hydroxyde de calcium, Ca(OH)2, est de 1,3 × 10-6. Calculez la solubilité molaire de l’hydroxyde de calcium.
Solution
La constante du produit de solubilité de l’hydroxyde de calcium est de 1,3 × 10-6.
La réaction est la suivante :
Ca(OH)2 (s) ⇌ Ca2+ (aq) + 2OH– (aq)
D’abord, écrivez l’expression constante de l’équilibre du produit de solubilité :
Ksp=[Ca2+][OH–]2
Créez un tableau ICE, en laissant la colonne Ca(OH)2 vide car elle est un solide et ne contribue pas au Ksp :
Ca(OH)2 ⇌ Ca2+ + 2OH–
|
Concentration initiale (M) |
|
0 |
0 |
|
Changement (M) |
|
x |
2x |
|
Concentration d’équilibre (M) |
|
0 + x = x |
0 +2x = 2x |
A l’équilibre :
Ksp=[Ca2+][OH–]2
1.3×10-6=(x)(2x)2=(x)(4x2)=4x3
x=1.3×10-643=6.9×10-3
Par conséquent, la solubilité molaire du Ca(OH)2 est de 1,3 × 10-2 M.
Vérifiez votre apprentissage 6.4.4 – Détermination de la solubilité molaire à partir du Ksp, Partie II
Le Ksp de PbI2 est de 1,4 × 10-8. Calculer la solubilité molaire de l’iodure de plomb(II).
Réponse
1.5 × 10–3 M
Notez que la solubilité n’est pas toujours donnée comme une valeur molaire. Lorsque la solubilité d’un composé est donnée dans une unité autre que les moles par litre, nous devons convertir la solubilité en moles par litre (c’est-à-dire la molarité) afin de l’utiliser dans l’expression constante du produit de solubilité. L’exemple suivant montre comment effectuer ces conversions d’unités avant de déterminer l’équilibre du produit de solubilité.
Exemple 6.4.6 – Détermination du Ksp à partir de la solubilité par gram
De nombreux pigments utilisés par les artistes dans les peintures à l’huile (figure 6.4.3.) sont peu solubles dans l’eau. Par exemple, la solubilité du pigment jaune de chrome de l’artiste, PbCrO4, est de 4,6 × 10-6 g/L. Déterminez la constante d’équilibre du produit de solubilité pour PbCrO4.

Figure 6.4.3. Les peintures à l’huile contiennent des pigments qui sont très légèrement solubles dans l’eau. Outre le jaune de chrome (PbCrO4), on peut citer le bleu de Prusse (Fe7(CN)18), la couleur rouge-orange vermillon (HgS) et la couleur verte verdienne (Cr2O3). (crédit : Sonny Abesamis)
Solution
On nous donne la solubilité du PbCrO4 en grammes par litre. Si nous convertissons cette solubilité en moles par litre, nous pouvons trouver les concentrations d’équilibre de Pb2+ et CrO42-, puis Ksp :

Utilisez la masse molaire de PbCrO4 (323,2g/mol) pour convertir la solubilité de PbCrO4 en grammes par litre en moles par litre :
PbCrO4] = (4.6×10-6g PbCrO4 / 1L) × (1 mol PbCrO4 / 323.2g PbCrO4)
= 1.4×10-8 mol PbCrO4 / 1L
= 1.4×10-8 M
L’équation chimique de la dissolution indique que 1 mole de PbCrO4 donne 1 mole de Pb2+(aq) et 1 mole de CrO42-(aq) :
PbCrO4 (s) ⇌ Pb2+ (aq) + CrO42- (aq)
Ainsi, à l’équilibre, [Pb2+] et [CrO42-] sont tous deux égaux à la solubilité molaire de PbCrO4 :
[Pb(aq)2+]=[CrO4(aq)2-]=1.4×10-8M
Résoudre. Ksp = [Pb2+] [CrO42-] = (1,4 × 10–8)(1,4 × 10-8) = 2,0 × 10-16
Vérifiez votre apprentissage 6.4.5 – Détermination du Ksp à partir de la solubilité par gram
La solubilité du chlorure de thallium(I) (TlCl), un intermédiaire formé lors de l’isolement du thallium à partir de minerais, est de 3,46 grammes par litre à 20°C. Quel est son produit de solubilité ?
Réponse
1.7 × 10–4
Exemple 6.4.7 – Calcul de la solubilité du Hg2Cl2
Le calomel, Hg2Cl2, est un composé composé de l’ion diatomique du mercure(I), Hg22+, et des ions chlorure, Cl-. Bien que la plupart des composés du mercure soient aujourd’hui connus pour être toxiques, les médecins du XVIIIe siècle utilisaient le calomel comme médicament. Leurs patients souffraient rarement d’un empoisonnement au mercure à la suite des traitements, car le calomel est assez insoluble :
Hg2Cl2 (s) ⇌ Hg2+ (aq) + 2Cl– (aq) Ksp=1.1×10-18
Calculer la solubilité molaire de Hg2Cl2.
Solution
La solubilité molaire de Hg2Cl2 est égale à la concentration d’ions Hg22+ car pour chaque mole de Hg2Cl2 qui se dissout, une mole de Hg22+ se forme :

Déterminer la direction du changement. Avant que le Hg2Cl2 ne se dissolve, Q est égal à zéro, et la réaction se déplacera vers la droite pour atteindre l’équilibre.
Déterminer les concentrations x et d’équilibre. Les concentrations et les variations sont indiquées dans le tableau suivant de la CIE :
Hg2Cl2 ⇌ Hg22+ + 2 Cl–
|
Concentration initiale (M) |
|
0 |
0 |
|
Changement (M) |
|
x |
2x |
|
Concentration d’équilibre (M) |
|
0 + x = x |
0 +2x = 2x |
Notez que la variation de la concentration de Cl- (2x) est deux fois plus importante que la variation de la concentration de Hg22+ (x) parce que 2 moles de Cl- se forment pour chaque mole de Hg22+ qui se forme. Le Hg2Cl2 est un solide pur, il n’apparaît donc pas dans le calcul.
Résoudre x et les concentrations d’équilibre. Nous substituons les concentrations d’équilibre dans l’expression pour Ksp et calculons la valeur de x :
Ksp=[Hg22+][Cl–]2
1.1×10-18=(x)(2x)2
4x3=1.1×10-18
x=1.1×10-1843=6.5×10-7M
[Hg22+]=6.5×10-7M=6.5×10-7M
[Cl–]=2x=2(6.5×10-7M)=1.3×10-6 M
La solubilité molaire de Hg2Cl2 est égale à [Hg22+], soit 6,5 × 10-7 M.
Vérifiez le travail. A l’équilibre, Q = Ksp :
Q=[Hg22+][Cl–]2=(6.5×10-7)(1.3×10-6)2=1.1×10-18
Les calculs sont vérifiés.
Vérifiez votre apprentissage 6.4.6 – Calcul de la solubilité du Hg2Cl2
Déterminer la solubilité molaire du MgF2 à partir de son produit de solubilité : Ksp = 6,4 × 10-9.
Réponse
1.2 × 10–3 M
Les valeurs de Ksp présentées sous forme de tableau peuvent également être comparées aux quotients de réaction calculés à partir de données expérimentales pour savoir si un solide va précipiter dans une réaction dans des conditions spécifiques : Q est égal à Ksp à l‘équilibre ; si Q est inférieur à Ksp, le solide se dissoudra jusqu’à ce que Q soit égal à Ksp ; si Q est supérieur à Ksp, la précipitation se produira à une température donnée jusqu’à ce que Q soit égal à Ksp.
|
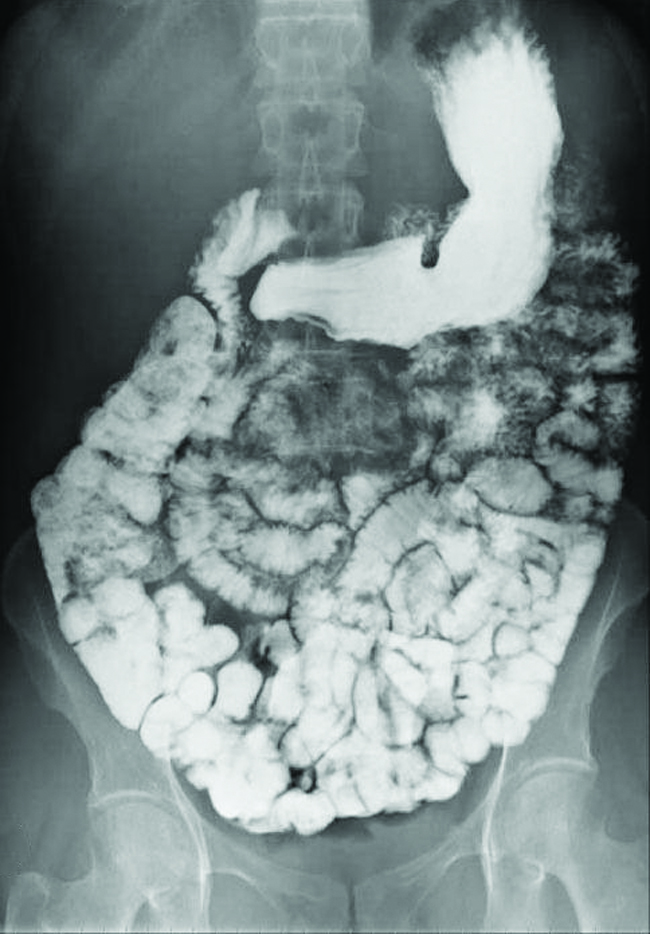
Utilisation du sulfate de baryum pour l’imagerie médicale Divers types de techniques d’imagerie médicale sont utilisés pour faciliter le diagnostic des maladies de manière non invasive. L’une de ces techniques utilise l’ingestion d’un composé de baryum avant de prendre une radiographie. Une suspension de sulfate de baryum, une poudre crayeuse, est ingérée par le patient. Comme le Ksp du sulfate de baryum est de 1,1 × 10-10, une très petite partie de celui-ci se dissout en recouvrant la paroi du tractus intestinal du patient. Les zones du tube digestif recouvertes de baryum apparaissent alors en blanc sur une radiographie, ce qui permet d’obtenir plus de détails visuels qu’avec une radiographie traditionnelle (figure 6.4.4.).
Figure 6.4.4. La suspension de sulfate de baryum recouvre le tractus intestinal, ce qui permet d’obtenir des détails visuels plus importants qu’avec une radiographie traditionnelle. (Modification du crédit de l’œuvre par « glitzy queen00″/Wikimedia Commons) D’autres tests diagnostiques peuvent être effectués à l’aide de sulfate de baryum et de la fluoroscopie. Dans la fluoroscopie, une radiographie continue est passée à travers le corps afin que le médecin puisse suivre, sur un écran de télévision ou d’ordinateur, le mouvement du sulfate de baryum lors de son passage dans le tube digestif. L’imagerie médicale utilisant le sulfate de baryum peut être utilisée pour diagnostiquer le reflux acide, la maladie de Crohn et les ulcères, en plus d’autres affections. Vous pouvez visiter ce site web pour obtenir de plus amples informations sur l’utilisation du baryum dans les diagnostics médicaux et sur les affections qu’il permet de diagnostiquer. |
L’effet des ions communs et la solubilité
Que se passe-t-il si nous essayons de dissoudre un sel peu soluble dans une solution aqueuse qui contient déjà un des ions du sel ? Après la section 6.1, ce serait un exemple de l'effet des ions communs. Selon le principe de Le Chatelier, la présence de l’ion produit déplace l’équilibre vers le réactif solide, et nous nous attendons à ce que la solubilité du sel soit réduite.
Exemple 6.4.8 – L’effet des ions communs et la solubilité
Si nous essayons de dissoudre le chlorure de plomb(II) dans une solution de chlorure de sodium à 0,100 M au lieu de l’eau, quelle est la concentration d’équilibre des ions de plomb(II), par rapport à l’eau pure ?
Réponse
D’abord, déterminons la solubilité du PbCl2 dans l’eau pure. Nous pouvons définir x comme étant la concentration des ions plomb(II) à l’équilibre, et utiliser une table de ICE :
PbCl2 ⇌ Pb2+ + 2 Cl-
|
Concentration initiale (M) |
|
0 |
0 |
|
Changement (M) |
|
x |
2x |
|
Concentration à l’équilibre (M) |
|
0 + x = x |
0 +2x = 2x |
Nous substituons les concentrations d’équilibre dans l’expression pour Ksp et calculons la valeur de x :
Ksp=[Pb2+][Cl–]2
1.7×10-5=(x)(2x)2
4x3=1.7×10-5
x=1.7×10-543=0.016M
Maintenant, pour trouver la solubilité du chlorure de plomb (II) dans le NaCl 0,100 M, nous répétons ce processus, mais nous ne tenons compte que de la présence de l’ion commun. Dans cet exemple, l’ion commun est l’ion chlorure. Comme NaCl est un sel soluble, nous supposons une ionisation de 100% et donc [Cl–]i = 0,100 M.
PbCl2 ⇌ Pb2+ + 2 Cl–
|
Concentration initiale (M) |
|
0 |
0.100 |
|
Changement (M) |
|
x |
2x |
|
Concentration d’équilibre (M) |
|
0 + x = x |
0.100 +2x |
Là encore, nous substituons les concentrations d’équilibre dans l’expression pour Ksp et calculons la valeur de x, et pour simplifier le calcul, nous supposons que la valeur de x est petite :
Ksp=[Pb2+][Cl–]2
1.7×10-5=(x)(0.100+2x)2
1.7×10-5=(x)(0.100)2
x=1.7×10-3M
Enfin, comparons les valeurs obtenues :
Solution originale:
[Pb2+]=0.016M
Dans une solution de NaCl à 0,100 M :
[Pb2+]=0.0017M
La concentration des ions plomb(II) a diminué d’un facteur d’environ 10, ce qui confirme que l’effet des ions communs inhibe la solubilité d’un sel peu soluble. Si des solutions plus concentrées de chlorure de sodium sont utilisées, la solubilité diminue encore.
Vérifiez votre apprentissage 6.4.7 – L’effet des ions communs et la solubilité
Le BaSO4 est un sel peu soluble qui s’ionise en Ba2+ et SO42- :
BaSO4 ⇌ Ba2+ + SO42-Ksp = 1.1×10-10
Trouvez la concentration de chaque ion à l’équilibre pour une solution saturée de sulfate de baryum. Ensuite, on ajoute du sulfate de lithium (Li2SO4) dans le récipient de réaction jusqu’à ce que sa concentration soit de 0,500 M. Quelle est la concentration des ions baryum et sulfate après l’ajout de sulfate de lithium ?
Réponse
Avant l’ajout de Li2SO4 :
= 1.0 x 10-5 M ,
= 1.0 x 10-5 M
Après ajout de Li2SO4 :
= 2.2 x 10-10 M ,
= 0.500 M
Vérifiez votre apprentissage 6.4.8 – L’effet des ions communs et la solubilité
Calculer la solubilité du carbonate d’argent dans une solution de 0,25 M de carbonate de sodium. Le Ksp du carbonate d‘argent est de 8,46 × 10-12 à 25°C.
Réponse
2,9 × 10-6 M (contre 1,3 × 10-4 M dans l’eau pure)
Effet du pH sur la solubilité
Pour certains sels, les concentrations en ions hydronium et hydroxyde peuvent influencer la solubilité, comme un cas particulier de l’effet des ions communs. En prenant le concept d’hydrolyse, introduit au chapitre 5, et en appliquant le principe de Le Chatelier aux sels peu solubles, nous pouvons le prévoir qualitativement :
Les sels acides seront moins solubles dans l’acide (pH < 7), et plus solubles dans la base (pH > 7)
Les sels BASIC seront moins solubles dans les bases (pH > 7), et plus solubles dans les acides (pH < 7)
Les sels neutres ont des solubilités non affectées par le pH
Prenons l’exemple de l’hydroxyde de cobalt (II). Il se dissout dans l’équilibre suivant :
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq)
Ksp = 2.5 x 10-16 = [Co2+][OH–]2
Nous pouvons comparer la solubilité de ce composé dans l’eau pure (où [OH–] = 1,0 x 10-7) à sa solubilité dans une solution tampon de pH = 6 (où [OH–] = 1,0 x 10-8), en utilisant les deux tableaux ICE suivants :
|
Eau pure, [OH-] = 1 x 10-7 M |
Tampon (pH = 6), [OH-] = 1 x 10-8 M |
||||||
|
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH- (aq) |
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH- (aq) |
||||||
|
I |
– |
0 |
1 x 10-7 |
I |
– |
0 |
1 x 10-8 |
|
C |
– |
+x |
+2x |
C |
– |
+x |
PAS de changement |
|
E |
– |
x |
1 x 10-7 +2x |
E |
– |
x |
1 x 10-8 |
|
Ksp = (x)(1,0 x 10-7 + 2x)2 s ≈ (x)(2x)2 s = 1,1 x 10-5 M |
Ksp = (x)(1,0 x 10-8)2 s = (Ksp)/(1,0 x 10-8)2 s > 50 M (soluble !) |
||||||
Les calculs ci-dessus montrent que le Co(OH)2, à l’origine peu soluble dans l’eau neutre, devient beaucoup plus soluble dans des conditions acides. Pourquoi en est-il ainsi ? Complétez l’exercice ci-dessous pour illustrer la raison.
Vérifiez votre apprentissage 6.4.9 – Effet du pH sur la solubilité
L’équilibre pour la dissolution de l’hydroxyde de cobalt (II) est :
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq) Ksp = 5.9 x 10–15
En solution acide, chaque ion hydroxyde produit est neutralisé par un ion hydronium. Comme nous l’avons vu au chapitre 5, l’équation ionique nette pour la neutralisation acide-base est l’inverse de l’autoionisation de l’eau :
OH– (aq) + H3O+ (aq) ⇋ 2 H2O(l) K = 1/Kw = 1.0 x 1014
Combinez les deux équilibres fournis, en tenant compte de la stœchiométrie, pour trouver une équation chimique globale pour la dissolution de l’hydroxyde de cobalt (II) en solution acide, ainsi que la valeur de la constante d’équilibre. (Rappeler les règles de manipulation des constantes d’équilibre du chapitre 4).
Réponse
Co(OH)2 (s) + 2H3O+ (aq) ⇋ Co2+ (aq) + 4H2O(l), K = 5.9 x 1013
Prévision des précipitations
L’équation qui décrit l’équilibre entre le carbonate de calcium solide et ses ions solvatés est la suivante :
CaCO3 (aq) ⇌ Ca2+ (aq) + CO32- (aq)
Nous pouvons établir cet équilibre soit en ajoutant du carbonate de calcium solide à l’eau, soit en mélangeant une solution qui contient des ions calcium avec une solution qui contient des ions carbonate. Si nous ajoutons du carbonate de calcium à l’eau, le solide se dissout jusqu’à ce que les concentrations soient telles que la valeur du quotient de réaction (Q = [Ca2+] [CO32-]) soit égale au produit de solubilité (Ksp = 8,7 × 10-9). Si l’on mélange une solution de nitrate de calcium, qui contient des ions Ca2+, avec une solution de carbonate de sodium, qui contient des ions CO32-, le solide ionique légèrement soluble CaCO3 précipitera, à condition que les concentrations des ions Ca2+ et CO32- soient telles que Q soit supérieur à Ksp pour le mélange. La réaction se déplace vers la gauche et les concentrations des ions sont réduites par la formation du solide jusqu’à ce que la valeur de Q soit égale à Ksp. Il en résulte une solution saturée en équilibre avec le solide non dissous. Si les concentrations sont telles que Q est inférieur à Ksp, alors la solution n’est pas saturée et aucun précipité ne se formera.
Nous pouvons comparer les valeurs numériques de Q avec celles de Ksp pour prédire si des précipitations vont se produire, comme le montre l’exemple suivant. (Note : Comme toutes les formes de constantes d’équilibre dépendent de la température, nous supposerons dans ce chapitre un environnement à température ambiante, à moins qu’une valeur de température différente ne soit explicitement spécifiée).
Exemple 6.4.8 – Précipitation de Mg(OH)2
La première étape de la préparation du magnésium métal est la précipitation de Mg(OH)2 dans l’eau de mer par l’ajout de chaux, Ca(OH)2, une source d’ion OH– peu coûteuse et facilement disponible :
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
La concentration de Mg2+(aq) dans l’eau de mer est de 0,0537 M. Le Mg(OH)2 précipitera-t-il lorsque suffisamment de Ca(OH)2 est ajouté pour donner un [OH–] de 0,0010 M ?
Solution
Ce problème pose la question de savoir si la réaction :
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH- (aq)
se déplace vers la gauche et forme un solide Mg(OH)2 lorsque [Mg2+] = 0,0537 M et [OH-] = 0,0010 M. La réaction se déplace vers la gauche si Q est supérieur à Ksp. Le calcul du quotient de réaction dans ces conditions est présenté ici :
Q = [Mg2+][OH–]2 = (0.0537)(0.0010)2 = 5.4 x 10-8
Comme Q est supérieur à Ksp (Q = 5,4 × 10-8 est supérieur à Ksp = 8,9 × 10-12), on peut s’attendre à ce que la réaction se déplace vers la gauche et forme de l’hydroxyde de magnésium solide. Mg(OH)2 (s) se forme jusqu’à ce que les concentrations d’ion magnésium et d’ion hydroxyde soient suffisamment réduites pour que la valeur de Q soit égale à Ksp.
Vérifiez votre apprentissage 6.4.10 – Précipitation de Mg(OH)2
KClO4 précipitera-t-il lorsque 20 ml d’une solution 0,050-M de K+ sont ajoutés à 80 ml d’une solution 0,50-M de ClO4– ? (N’oubliez pas de calculer la nouvelle concentration de chaque ion après avoir mélangé les solutions avant de vous brancher sur l’expression du quotient de réaction).
Réponse
Non, Q = 4,0 × 10-3, ce qui est inférieur à Ksp = 1,05 × 10-2
Dans l’exemple précédent, nous avons vu qu’un précipité se forme lorsque Q est supérieur à Ksp. En général, selon l’équation 6.4.1, lorsqu’une solution d’un sel soluble de l’ion Mm+ est mélangée avec une solution d’un sel soluble de l’ion Xn–, le solide MpXq précipite si la valeur de Q pour le mélange de Mm+ et Xn– est supérieure à Ksp pour MpXq. Ainsi, si nous connaissons la concentration de l’un des ions d’un solide ionique légèrement soluble et la valeur du produit de solubilité du solide, nous pouvons calculer la concentration que l’autre ion doit dépasser pour que la précipitation commence. Pour simplifier le calcul, nous supposerons que la précipitation commence lorsque le quotient de réaction devient égal à la constante du produit de solubilité.
Exemple 6.4.9 – Précipitation de l’oxalate de calcium
Le sang ne coagule pas si les ions calcium sont éliminés du plasma. Certains tubes de prélèvement sanguin contiennent des sels de l’ion oxalate, C2O42-, à cet effet (figure 6.4.5.). À des concentrations suffisamment élevées, les ions calcium et oxalate forment de l’oxalate de calcium solide monohydraté, CaC2O4-H2O. La concentration de Ca2+ dans un échantillon de sérum sanguin est de 2,2 × 10-3 M. Quelle concentration d’ion C2O42- doit être établie avant que le CaC2O4-H2O ne commence à précipiter ?
Figure 6.4.5. On peut ajouter au sang des anticoagulants qui se combineront aux ions Ca2+ du sérum sanguin et empêcheront le sang de coaguler. (crédit : modification du travail par Neeta Lind)
Solution
L’expression d’équilibre est :
CaC2O4 (s) ⇌ Ca2+ (aq) + C2O42- (aq)
Pour cette réaction :
Ksp=[Ca2+][C2O42-]=1.96×10-8
Le CaC2O4 solide ne commence à se former que lorsque Q est égal à Ksp. Comme nous connaissons Ksp et [Ca2+], nous pouvons déterminer la concentration de C2O42- nécessaire pour produire la première trace de précipité solide :
Q=Ksp=[Ca2+(aq)][C2O42-(aq)]=1.96×10-8
(2.2×10-3)[C2O42-(aq)] = 1.96×10-8
Une concentration de [C2O42-] = 8,9 × 10-6 M est nécessaire pour déclencher la précipitation du CaC2O4 dans ces conditions.
Vérifiez votre apprentissage 6.4.11 – Précipitation de l’oxalate de calcium
Si une solution contient 0,0020 mol de CrO42- par litre, quelle concentration d’ion Ag+ doit être atteinte en ajoutant de l’AgNO3 solide avant que l’Ag2CrO4 ne commence à précipiter ? Négliger toute augmentation de volume lors de l’ajout du nitrate d’argent solide.
Réponse
4.5 × 10–9 M
Il est parfois utile de connaître la concentration d’un ion qui reste en solution après la précipitation. Nous pouvons également utiliser le produit de la solubilité pour ce calcul : Si nous connaissons la valeur de Ksp et la concentration d’un ion en solution, nous pouvons calculer la concentration du second ion restant en solution. Le calcul est du même type que celui de l’exemple précédent – calcul de la concentration d’une espèce dans un mélange d’équilibre à partir des concentrations des autres espèces et de la constante d’équilibre. Cependant, les concentrations sont différentes ; nous calculons les concentrations après la fin de la précipitation, plutôt qu’au début de la précipitation.
Exemple 6.4.10 – Concentrations après les précipitations
Les vêtements lavés dans une eau dont la concentration en ion manganèse (II) (Mn2+) dépasse 0,1 mg/L (1,8 × 10-6 M) peuvent être colorés par le manganèse lors de l’oxydation, mais la quantité de Mn2+ dans l’eau peut être réduite par l’ajout d’une base. Si une personne qui fait la lessive souhaite ajouter un tampon pour maintenir le pH suffisamment élevé pour précipiter le manganèse sous forme d’hydroxyde, Mn(OH)2, quel est le pH nécessaire pour maintenir [Mn2+] égal à 1,8 × 10-6 M ?
Solution
La dissolution du Mn(OH)2 est décrite par l’équation :
Mn(OH)2 (s) ⇌ Mn2+ (aq) + 2OH– (aq) Ksp=2×10-3
Nous devons calculer la concentration de OH- lorsque la concentration de Mn2+ est de 1,8 × 10-6 M. À partir de là, nous calculons le pH. A l’équilibre :
Ksp=[Mn2+][OH–]2
Ou
(1.8×10-6)[OH–]2=2×10-3
Donc
[OH–] = 3.3×10-4 M
Maintenant, nous calculons le pH à partir du pOH :
pOH=-log[OH–]=-log(3.3×10-4)=3.48
pH=14.00-pOH=14.00-3.80=10.52
Si la personne qui fait la lessive ajoute une base, comme le silicate de sodium (Na4SiO4) de certains détergents, à l’eau de lavage jusqu’à ce que le pH soit porté à 10,52, l’ion manganèse sera réduit à une concentration de 1,8 × 10-6 M ; à cette concentration ou moins, l’ion ne tachera pas les vêtements.
Vérifiez votre apprentissage 6.4.12 – Concentrations après les précipitations
La première étape de la préparation du magnésium métal est la précipitation de Mg(OH)2 dans l’eau de mer par l’ajout de Ca(OH)2. La concentration de Mg2+(aq) dans l’eau de mer est de 5,37 × 10-2 M. Calculez le pH auquel [Mg2+] est ramené à 1,0 × 10-5 M par l’addition de Ca(OH)2.
Réponse
10.97
En raison de leur sensibilité à la lumière, les mélanges d’halogénures d’argent sont utilisés dans les fibres optiques pour les lasers médicaux, dans les verres de lunettes photochromiques (lentilles de verre qui s’assombrissent automatiquement lorsqu’elles sont exposées à la lumière du soleil), et – avant l’avènement de la photographie numérique – dans les pellicules photographiques. Même si AgCl (Ksp = 1,6 × 10-10), AgBr (Ksp = 5,0 × 10-13) et AgI (Ksp = 1,5 × 10-16) sont tous trois assez insolubles, nous ne pouvons pas préparer un mélange solide homogène de ces halogénures en ajoutant Ag+ à une solution de Cl–, Br–, et I– ; la quasi-totalité de l’AgI précipitera avant la formation de tout autre halogénure solide en raison de sa plus faible solubilité molaire. Cependant, nous pouvons préparer un mélange homogène des solides en ajoutant lentement une solution de Cl–, Br–, et I– à une solution de Ag+.
Lorsque deux anions forment des composés légèrement solubles avec le même cation, ou lorsque deux cations forment des composés légèrement solubles avec le même anion, le composé le moins soluble (le composé ayant la plus faible solubilité molaire) précipite généralement en premier lorsque nous ajoutons un agent de précipitation à une solution contenant les deux anions (ou les deux cations). Lorsque les solubilités molaires des deux composés diffèrent de deux ordres de grandeur ou plus (par exemple, 10-2 contre 10-4), presque tout le composé le moins soluble précipite avant le plus soluble. Il s’agit d’un exemple de précipitation sélective, où un réactif est ajouté à une solution d’ions dissous, provoquant la précipitation d’un des ions avant le reste.
|
Le rôle des précipitations dans le traitement des eaux usées Les équilibres de solubilité sont des outils utiles pour le traitement des eaux usées effectué dans des installations susceptibles de traiter les eaux municipales de votre ville (figure 6.4.6.). Plus précisément, la précipitation sélective est utilisée pour éliminer les contaminants des eaux usées avant qu’elles ne soient rejetées dans les masses d’eau naturelles. Par exemple, les ions de phosphate (PO42-) sont souvent présents dans l’eau rejetée par les installations de fabrication. Une abondance de phosphate entraîne la croissance d’un excès d’algues, ce qui a un impact sur la quantité d’oxygène disponible pour la vie marine et rend l’eau impropre à la consommation humaine.
Figure 6.4.6. Les installations de traitement des eaux usées, telles que celle-ci, éliminent les contaminants des eaux usées avant que l’eau ne soit rejetée dans le milieu naturel. (crédit : « eutrophisation&hypoxie« /Wikimedia Commons) Une façon courante d’éliminer les phosphates de l’eau est l’ajout d’hydroxyde de calcium, connu sous le nom de chaux, Ca(OH)2. La chaux est transformée en carbonate de calcium, une base forte, dans l’eau. Lorsque l’eau devient plus basique, les ions de calcium réagissent avec les ions de phosphate pour produire de l’hydroxylapatite, Ca5(PO4)3(OH), qui précipite ensuite hors de la solution : 5Ca2++3PO43-+OH-↔Ca10(PO4)6⋅(OH)2(s) Le précipité est ensuite éliminé par filtration et l’eau est ramenée à un pH neutre par l’ajout de CO2 dans un processus de recarbonatation. D’autres produits chimiques peuvent également être utilisés pour l’élimination des phosphates par précipitation, notamment le chlorure de fer(III) et le sulfate d’aluminium. Consultez ce site pour plus d’informations sur la manière dont le phosphore est éliminé des eaux usées. |
Les précipitations sélectives peuvent également être utilisées dans l’analyse qualitative. Dans cette méthode, des réactifs sont ajoutés à un mélange chimique inconnu afin d’induire une précipitation. Certains réactifs provoquent la précipitation d’ions spécifiques ; par conséquent, l’ajout du réactif peut être utilisé pour déterminer si l’ion est présent dans la solution.
Visualisez cette simulation pour étudier le processus de dissolution des sels et de formation de solutions saturées et de précipités pour des composés spécifiques, ou des composés pour lesquels vous sélectionnez les charges sur les ions et le Ksp.
Exemple 6.4.11 – Précipitation des halogénures d’argent
Une solution contient 0,0010 mole de KI et 0,10 mole de KCl par litre. De l’AgNO3 est progressivement ajouté à cette solution. Quelles sont les premières formes, AgI solide ou AgCl solide ?
Solution
Les deux équilibres en cause sont :
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq) Ksp=1.6×10-10
AgI (s) ⇌ Ag+ (aq) + I– (aq) Ksp=1.5×10-16
Dans cet exemple, les deux sels forment le même nombre d’ions (1 mole de solide dissous produit 1 mole de cations et 1 mole d’anions) et donc dans les deux cas, la valeur Ksp est calculée comme le carré de la solubilité molaire (c’est-à-dire si la solubilité molaire est x, Ksp = x2). Par conséquent, nous pouvons comparer directement ces valeurs Ksp pour obtenir une idée qualitative de l’ordre des précipitations. Notez que les valeurs de Ksp ne peuvent PAS être comparées directement si le nombre d’ions formés à l’équilibre de dissolution n’est pas identique (par exemple, il ne serait pas approprié de comparer la valeur de Ksp de AgCl à celle de Ag2SO4).
Heureusement, dans ce cas, puisque les valeurs de Ksp sont corrélées de manière identique à la solubilité molaire de chaque solide (Ksp = x2), cela signifie que nous pouvons déduire que si la solution contenait des concentrations à peu près égales de Cl– et I–, alors le sel d’argent ayant le plus petit Ksp (AgI) précipiterait en premier. Les concentrations ne sont cependant pas égales, nous devrions donc trouver le [Ag+] à partir duquel l’AgCl commence à précipiter et le [Ag+] à partir duquel l’AgI commence à précipiter. Le sel qui se forme au niveau inférieur [Ag+] précipite en premier.
Pour AgI : AgI précipite lorsque Q est égal à Ksp pour AgI (1,5 × 10-16). Lorsque [I–] = 0,0010 M :
Q = [Ag+][I–] = [Ag+](0.0010) = 1.5×10-16
[Ag+] = (1.8×10-10)(0.10)= 1.6×10-9 M
L’AgI commence à précipiter lorsque [Ag+] est égal à 1,5 × 10-13 M.
Pour l’AgCl : L’AgCl précipite lorsque Q est égal à Ksp pour l’AgCl (1,6 × 10-10). Lorsque [Cl–] = 0,10 M :
Qsp=[Ag+][Cl–]=[Ag+](0.10)=1.6×10-10
[Ag+] = 1.8×10-10(0.10) =1.6×10-9 M
L’AgCl commence à précipiter lorsque [Ag+] est égal à 1,6 × 10-9 M.
L’AgI commence à précipiter à un niveau plus bas [Ag+] que l’AgCl, donc l’AgI commence à précipiter en premier.
Vérifiez votre apprentissage 6.4.13 – Précipitation des halogénures d’argent
Si l’on ajoute une solution de nitrate d’argent à une solution contenant 0,050 M d’ions Cl– et Br–, à partir de quel [Ag+] la précipitation commence-t-elle et quelle est la formule du précipité ?
Réponse
[Ag+] = 1,0 × 10-11 M ; AgBr précipite en premier
Questions
★ Questions
- Écrivez l’équation ionique de la dissolution et l’expression Ksp pour chacun des composés ioniques légèrement solubles suivants :
(a) LaF3
(b) CaCO3
(c) Ag2SO4
(d) Pb(OH)2
2. Le Manuel de chimie et de physique donne les solubilités des composés suivants en grammes par 100 ml d’eau. Comme ces composés ne sont que légèrement solubles, supposons que le volume ne change pas lors de la dissolution et calculons le produit de solubilité pour chacun d’entre eux.
(a) BaSeO4, 0.0118 g/100 mL
(b) Ba(BrO3)2·H2O, 0.30 g/100 mL
(c) NH4MgAsO4·6H2O, 0.038 g/100 mL
(d) La2(MoO4)3, 0.00179 g/100 mL
3. Utilisez des produits de solubilité et prévoyez lequel des sels suivants est le plus soluble, en termes de moles par litre, dans l’eau pure : CaF2, Hg2Cl2, PbI2 ou Sn(OH)2.
4. En supposant qu’aucun équilibre autre que la dissolution n’est impliquée, calculer la solubilité molaire de chacun des éléments suivants à partir de son produit de solubilité :
(a) KHC4H4O6
(b) PbI2
(c) Ag4[Fe(CN)6], un sel contenant l’ion Fe(CN)4
(d) Hg2I2
★★ Questions
5. En supposant qu’aucun équilibre autre que la dissolution n’est impliquée, calculer la concentration de toutes les espèces de solutés dans chacune des solutions de sels suivantes en contact avec une solution contenant un ion commun. Montrez que les changements dans les concentrations initiales des ions communs peuvent être négligés.
(a) AgCl(s) dans 0,025 M NaCl
(b) CaF2(s) en 0,00133 M KF
(c) Ag2SO4(s) dans 0,500 L d’une solution contenant 19,50 g de K2SO4
(d) Zn(OH)2(s) dans une solution tamponnée à un pH de 11,45
6. La plupart des composés de baryum sont très toxiques ; cependant, le sulfate de baryum est souvent administré par voie interne pour faciliter l’examen radiologique du tractus intestinal inférieur (figure 6.4.4). Cette utilisation de BaSO4 est possible en raison de sa faible solubilité. Calculer la solubilité molaire de BaSO4 et la masse de baryum présente dans 1,00 L d’eau saturée en BaSO4.
7. Le produit de solubilité du CaSO4-2H2O est de 2,4 × 10-5. Quelle masse de ce sel se dissoudra dans 1,0 L de SO42- 0,010 M ?
8. Lesquels des carbonates suivants se formeront en premier ? Lesquels des carbonates suivants se formeront en dernier ? Expliquez.
(a) MgCO3 Ksp = 3.5 × 10−8
(b) CaCO3 Ksp = 4.2 × 10−7
(c) SrCO3 Ksp = 3.9 × 10−9
(d) BaCO3 Ksp = 4.4 × 10−5
(e) MnCO3 Ksp = 5.1 × 10−9
9. Combien de grammes de Lait de Magnésium, Mg(OH)2 (s) (58,3 g/mol), seraient solubles dans 200 ml d’eau. Ksp = 7,1 × 10-12. Incluez la réaction ionique et l’expression pour Ksp dans votre réponse. (Kw = 1 × 10-14 = [H3O+] [OH–])
10. Un volume de 0,800 L d’une solution de Ba(NO3)2 de 2 × 10-4 M est ajouté à 0,200 L de Li2SO4 de 5 × 10-4 M. Le BaSO4 précipite-t-il ? Expliquez votre réponse.
11. Calculer la concentration de PO43- lorsque Ag3PO4 commence à précipiter à partir d’une solution qui est de 0,0125 M dans Ag+.
Réponses
- (a) LaF3 (s) ⇌ La3+ (aq) + 3F– (aq)
(b) CaCO3 (s) ⇌ Ca3+ (aq) + CO32- (aq)
(c) Ag2SO4 (s) ⇌ 2Ag+ (aq) + SO42- (aq)
(d) Pb(OH)2 (s) ⇌ Pb2+ (aq) + 2OH– (aq)
2. (a)1.77 × 10–7; (b) 1.6 × 10–6; (c) 2.2 × 10–9; (d) 7.91 × 10–22
3. La PbI2 est la plus soluble.
4. a) 2 × 10–2 M; (b) 1.5 × 10–3 M; (c) 2.27 × 10–9 M; (d) 2.2 × 10–10 M
5. (a)
(b)
,
Vérifiez:
,
Cette valeur est inférieure à 5 % et peut être ignorée.
(c)
,
Check:
la condition est remplie
(d)
,
Vérifiez :
x est inférieur à 5 % de
et est, par conséquent, négligeable.
6. La solubilité molaire de BaSO4 est de 1,51 × 10-4 M et la masse de baryum présente dans 1 L d’eau dans 0,020 g.
7. Masse (CaSO4·2H2O) = 0.72 g/L
8. Le MnCO3 se formera en premier, puisqu’il a la plus petite valeur de Ksp ; il est le moins soluble. Le MnCO3 sera le dernier à précipiter, car il a la plus grande valeur de Ksp.
1.23×10-3g Mg(OH)2
10. Aucune précipitation ne se produit car la valeur du produit de solubilité (2,3 x 10-8) est supérieure à celle du produit ionique (1,6 x 10-8).
11. 9.2 × 10−13 M
Mesure dans laquelle un soluté peut être dissous dans l'eau ou dans un solvant quelconque
De concentration égale à la solubilité ; contenant la concentration maximale de soluté possible pour une température et une pression donnée
de concentration qui dépasse la solubilité (plus que la quantité maximale normale de soluté qu'il contient) ; un état de non-équilibre
Produit insoluble qui se forme à partir de la réaction de réactifs solubles
Constante d'équilibre pour la dissolution d'un composé ionique
Solubilité d'un composé exprimée en unités de moles par litre (mol/L)
Produit des concentrations des ions en solution portées aux mêmes puissances que dans l'expression du produit de solubilité ; analogue au quotient de réaction (Q) discuté pour les équilibres gazeux
Produit insoluble qui se forme à partir de la réaction de réactifs solubles
Effet sur l'équilibre lorsqu'une substance ayant un ion en commun avec l'espèce dissoute est ajoutée à la solution ; provoque une diminution de la solubilité d'une espèce ionique, ou une diminution de l'ionisation d'un acide ou d'une base faible
Procédé de séparation d'ions utilisant des différences de solubilité avec un réactif de précipitation donné