6.3 – Réactions et titrages acide-base

Dans un titrage acide-base, une burette est utilisée pour délivrer des volumes mesurés d’une solution d’acide ou de base de concentration connue (le titrant) à un flacon qui contient une solution d’une base ou d’un acide, respectivement, de concentration inconnue (l’inconnu, ou analyte). Si la concentration du titrant est connue, alors la concentration de l’inconnu peut être déterminée. La discussion suivante porte sur les changements de pH qui se produisent lors d’un titrage acide-base. En traçant le pH de la solution dans le flacon en fonction de la quantité d’acide ou de base ajoutée, on obtient une courbe de titrage. La forme de la courbe fournit des informations importantes sur ce qui se passe dans la solution pendant le titrage.

Indicateurs acide-base

Certaines substances organiques changent de couleur dans une solution diluée lorsque la concentration en ions hydronium atteint une valeur particulière. Par exemple, la phénolphtaléine est une substance incolore dans toute solution aqueuse dont la concentration en ions hydronium est supérieure à 5,0 × 10^-9 M (pH < 8,3). Dans les solutions plus basiques où la concentration d’ions hydronium est inférieure à 5,0 × 10^-9 M (pH > 8,3), elle est rouge ou rose. Les substances telles que la phénolphtaléine, qui peuvent être utilisées pour déterminer le pH d’une solution, sont appelées indicateurs acido-basiques. Les indicateurs acide-base sont soit des acides organiques faibles, soit des bases organiques faibles.

Prenons le méthyl orange comme exemple d’indicateur acido-basique. Comme cette molécule organique est un acide faible, nous la représenterons à l’aide de HIn (comme nous utilisons “HA” pour représenter un acide faible générique). Le méthyl orange, HIn, existe donc en équilibre dans une solution aqueuse avec sa forme ionisée, la base conjuguée In-^, et nous pouvons décrire cela par la constante d’équilibre K_In :

HIn (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + In⁻ (aq)

rouge jaune

K_In= ([H₃O⁺][In^–])/[HIn]=4.0×10^-4

L’anion du méthyl orange, In-, est jaune, et la forme syndiquée, HIn, est rouge. Lorsque nous ajoutons de l’acide à une solution de méthyl orange, l’augmentation de la concentration en ions hydronium déplace l’équilibre vers la forme rouge syndiquée, conformément au principe de Le Châtelier. Si nous ajoutons une base, nous déplaçons l’équilibre vers la forme jaune. Ce comportement est tout à fait analogue à l’action des tampons.

La couleur d’un indicateur est le résultat visible du rapport des concentrations des deux espèces In- et HIn. Si la plus grande partie de l’indicateur (généralement environ 60-90 % ou plus) est présente sous forme d’In-, on voit alors la couleur de l’ion In-, qui serait jaune pour le méthyl orange. Si la plus grande partie est présente sous forme de HIn, alors nous voyons la couleur de la molécule HIn : rouge pour le méthyl orange. Pour le méthyl orange, nous pouvons réarranger l’équation pour K_In et écrire :

[In-]/[HIn]=[substance with yellow color]/[substance with red color] = K_In/[H3O+]

Cela nous montre comment le ratio de [In^–]/[HIn] varie en fonction de la concentration de l’ion hydronium. L’expression ci-dessus décrivant l’équilibre de l’indicateur peut être réarrangée :

[H₃O⁺]/K_In = [HIn]/[In^–]

log([H₃O⁺]/K_In)= log([HIn]/[In^–])

log([H₃O⁺])-log(K_In)=-log([In^–]/[HIn])

-pH+pK_In = -log([In^–]/[HIn])

pH = pK_In + log([In^–]/[HIn])

La dernière formule est la même que l’équation de Henderson-Hasselbalch, ce qui signifie que cette équation peut également être appliquée pour décrire l’équilibre des indicateurs.

Lorsque [H₃O+] a la même valeur numérique que KIn, le rapport de [In^–] à [HIn] est égal à 1, ce qui signifie que 50% de l’indicateur est présent sous la forme rouge (HIn) et 50% sous la forme ionique jaune (In-^), et que la solution apparaît de couleur orange. Lorsque la concentration en ions hydronium augmente jusqu’à 8 × 10^-4 M (un pH de 3,1), la solution devient rouge. Aucun changement de couleur n’est visible en cas d’augmentation supplémentaire de la concentration en ions hydronium (diminution du pH). À une concentration d’ions hydronium de 4 × 10^-5 M (un pH de 4,4), la plus grande partie de l’indicateur se trouve sous la forme ionique jaune, et une nouvelle diminution de la concentration d’ions hydronium (augmentation du pH) ne produit pas de changement de couleur visible. La plage de pH comprise entre 3,1 (rouge) et 4,4 (jaune) est l’intervalle de changement de couleur du méthyl-orange ; le changement de couleur prononcé a lieu entre ces valeurs de pH.

De nombreuses substances différentes peuvent être utilisées comme indicateurs, en fonction de la réaction particulière à surveiller. Par exemple, les anthocyanes sont une classe de molécules organiques que l’on trouve dans les fruits, les légumes, les céréales et les fleurs, et leur couleur dépend fortement du pH. Leur couleur change progressivement du rouge au jaune au fur et à mesure que le pH passe de 1 à 13 (voir le tableau 6.3.1 ci-dessous). Dans tous les cas, cependant, un bon indicateur doit avoir les propriétés suivantes :

Le changement de couleur doit être facilement détectable.

Le changement de couleur doit être rapide.

La molécule indicatrice ne doit pas réagir avec la substance titrée.

Pour réduire les erreurs, l’indicateur doit avoir un pK_In qui se situe dans une unité de pH du pH attendu au point d’équivalence du titrage.

Figure 6.3.1. Solutions aqueuses d’anthocyanes extraites de pétunias.

Tableau 6.3.1 Couleur et pH des anthocyanes

Des indicateurs synthétiques ont été développés qui répondent à ces critères et couvrent pratiquement toute la gamme des pH. La figure 6.3.2 montre la gamme approximative de pH sur laquelle certains indicateurs courants changent de couleur et leur changement de couleur. En outre, certains indicateurs (comme le bleu de thymol) sont des acides ou des bases polyprotiques, qui changent de couleur deux fois à des valeurs de pH très différentes.

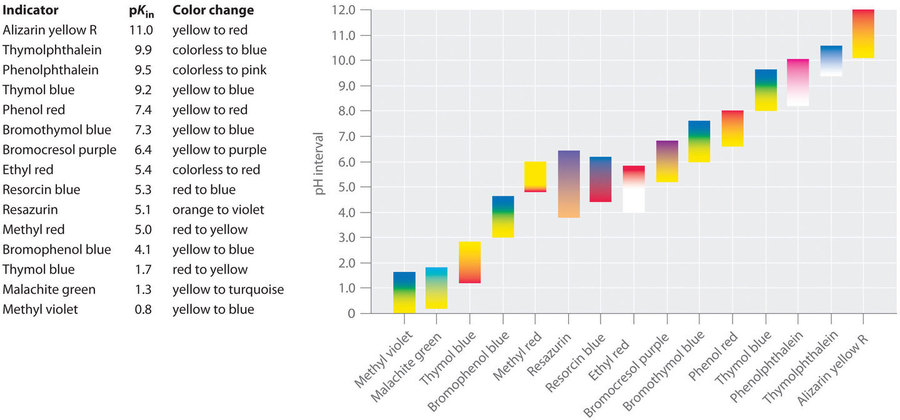
Figure 6.3.2. Quelques indicateurs communs acide-base. Les couleurs approximatives sont indiquées, ainsi que les valeurs pK_In et la plage de pH sur laquelle la couleur change.

Il est important de savoir qu’un indicateur ne change pas brusquement de couleur à une valeur de pH donnée ; au contraire, il subit un titrage comme tout autre acide ou base. Lorsque la concentration de HIn diminue et que la concentration de In- augmente, la couleur de la solution passe lentement de la couleur caractéristique de HIn à celle de In-. Comme nous le verrons plus tard, la  [In^–]/[HIn] passe de 0,1 à un pH inférieur d’une unité au pKIn à 10 à un pH supérieur d’une unité au pK_In. Ainsi, la plupart des indicateurs changent de couleur sur une plage de pH d’environ deux unités de pH.

Nous avons déclaré qu’un bon indicateur doit avoir une valeur pK_In proche du pH attendu au point d’équivalence. Pour un titrage à forte teneur en acide et en base, le choix de l’indicateur n’est pas particulièrement critique en raison de la très grande variation du pH qui se produit autour du point d’équivalence (nous verrons cela plus tard). En revanche, utiliser le mauvais indicateur pour un titrage d’un acide faible ou d’une base faible peut entraîner des erreurs relativement importantes.

L’importance du choix de l’indicateur est illustrée dans la figure 6.3.3. Cette figure montre les courbes du pH en fonction du volume de base ajoutée pour deux courbes de titrage distinctes : une solution 0,100 M de NaOH est utilisée pour titrer a) 50,0 ml d’une solution 0,100 M d’un acide fort (HCl) et b) 50,0 ml d’une solution 0,100 M d’un acide faible (CH₃COOH). Pour ces deux titrages, le nombre de moles d’acide initial présent est de 0,00500 mol (0,100 molL^-1 x 0,0500 L). Le point d'équivalence du titrage se produit lorsque la quantité de base ajoutée est égale à la quantité d’acide initial. Comme 0,00500 mol d’acide est présent dans les deux titrages, dans les deux cas, le point d’équivalence se produit lorsqu’exactement 50,0 ml de NaOH 0,100 M ont été ajoutés. Notez que, pour les deux titrages, les courbes deviennent presque verticales autour de 50,0 ml de NaOH ajouté : comme nous sommes proches du point d’équivalence autour de ce volume, chaque goutte de NaOH provoque une augmentation relativement forte du pH de la solution.

La figure montre également les plages de pH sur lesquelles deux indicateurs communs (le rouge de méthyle, pKIn = 5,0, et la phénolphtaléine, pKIn = 9,5) changent de couleur. Les barres horizontales indiquent les plages de pH sur lesquelles les deux indicateurs changent de couleur. Notez que pour la courbe de titrage du HCl, les deux indicateurs ont des plages de pH qui se situent complètement dans la partie verticale de la courbe de titrage. Par conséquent, les deux indicateurs changent de couleur autour du point d’équivalence, lorsqu’environ 50 ml de NaOH ont été ajoutés. Par conséquent, ces deux indicateurs pourraient être utilisés dans le titrage de l’acide fort.

En revanche, le titrage de l’acide acétique donnera des résultats très différents selon que l’on utilise comme indicateur le rouge de méthyle ou la phénolphtaléine. La phénolphtaléine présente une plage de pH qui se situe dans la partie verticale de la courbe de titrage. Par conséquent, le changement de couleur devrait être proche du point d’équivalence et la solution deviendra rose lorsqu’environ 50 ml de NaOH auront été ajoutés. En revanche, le rouge de méthyle commence à passer du rouge au jaune autour du pH 5, qui est proche du point médian du titrage de l’acide acétique, et non du point d’équivalence. L’ajout d’environ 25-30 ml de NaOH seulement entraîne donc un changement de couleur de l’indicateur rouge de méthyle, ce qui entraîne une énorme erreur.

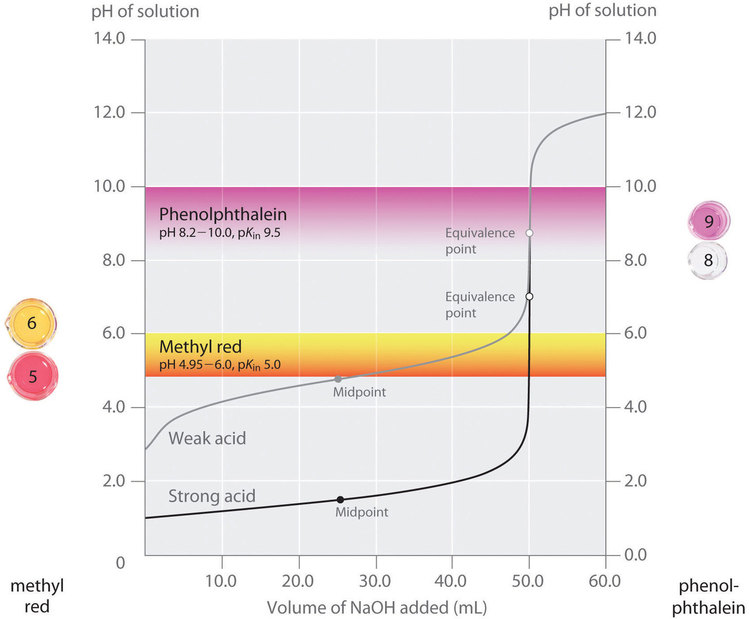
Figure 6.3.3. Choix de l’indicateur correct pour un titrage acide-base

La figure 6.3.3. montre les résultats obtenus en utilisant deux indicateurs (rouge de méthyle et phénolphtaléine) pour le titrage de solutions 0,100 M d’un acide fort (HCl) et d’un acide faible (acide acétique) avec du NaOH 0,100 M. En raison de la pente de la courbe de titrage d’un acide fort autour du point d’équivalence, l’un ou l’autre indicateur changera rapidement de couleur au point d’équivalence pour le titrage de l’acide fort. En revanche, le pK_In du rouge de méthyle (5,0) est très proche du pKa de l’acide acétique (4,76) ; le point médian du changement de couleur du rouge de méthyle se situe près du point médian du titrage, plutôt qu’au point d’équivalence.

En général, pour les titrages d’acides forts avec des bases fortes (et vice versa), tout indicateur ayant un pKin compris entre environ 4,0 et 10,0 fera l’affaire. Pour le titrage d’un acide faible, cependant, le pH au point d’équivalence est supérieur à 7,0, de sorte qu’un indicateur tel que la phénolphtaléine ou le bleu de thymol, avec un pK_In > 7,0, est plus approprié. Inversement, pour le titrage d’une base faible, lorsque le pH au point d’équivalence est inférieur à 7,0, un indicateur tel que le rouge de méthyle ou le bleu de bromocrésol, avec un pK_In < 7,0, doit être utilisé.

L’existence de nombreux indicateurs différents avec des couleurs et des valeurs pK_In différentes permet également d’estimer le pH d’une solution sans utiliser un coûteux pH-mètre électronique et une électrode pH fragile. Des bandes de papier ou de plastique imprégnées de combinaisons d’indicateurs sont utilisées comme “papier pH”, qui permet d’estimer le pH d’une solution en y trempant simplement un morceau de papier pH et en comparant la couleur résultante avec les étalons imprimés sur le récipient (figure 6.3.4.).

Figure 6.3.4. Papier pH. Le papier pH contient un ensemble d’indicateurs qui changent de couleur à différentes valeurs de pH. Le pH approximatif d’une solution peut être déterminé en trempant simplement une bande de papier dans la solution et en comparant la couleur aux normes fournies.

Titrages des acides forts et des bases

La figure 6.3.2 (a) montre un graphique du pH lorsque du HCl 0,20 M est progressivement ajouté à 50,00 ml d’eau pure. Le pH de l’échantillon dans le flacon est initialement de 7,00 (comme prévu pour l’eau pure), mais il diminue très rapidement au fur et à mesure que l’on ajoute du HCl. Le pH finit par s’approcher d’une limite lorsque la concentration de l’échantillon s’approche de sa valeur maximale (0,20 M HCl). En revanche, la figure 6.3.1 (b) montre que lorsque du NaOH 0,20 M est ajouté à 50,00 ml d’eau distillée, le pH (initialement 7,00) monte très rapidement au début, mais ensuite plus progressivement, pour finalement approcher une limite lorsque la concentration de NaOH s’approche de son maximum. Comme vous pouvez le voir sur ces graphiques, la courbe de pH pour l’ajout d’une base est l’image miroir de la courbe pour l’ajout d’un acide.

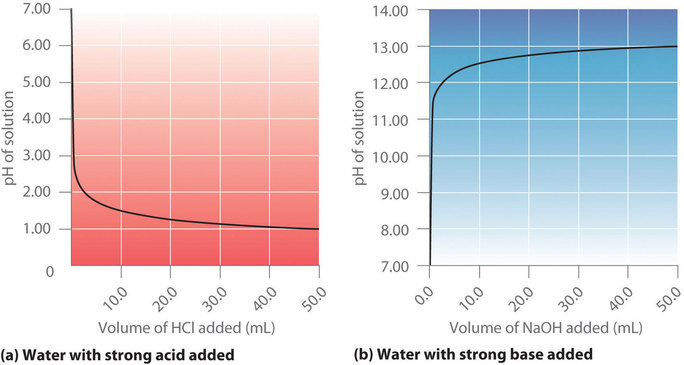
Figure 6.3.2. pH de la solution en fonction du volume d’un acide fort ou d’une base forte ajouté à l’eau distillée. (a) Lorsque du HCl 0,20 M est ajouté à 50,0 ml d’eau distillée, le pH diminue rapidement jusqu’à atteindre un minimum (le pH du HCl 0,20 M). (b) Inversement, lorsque du NaOH 0,20 M est ajouté à 50,0 ml d’eau distillée, le pH augmente rapidement jusqu’à atteindre un maximum (le pH du NaOH 0,20 M).

Supposons que nous ajoutions maintenant du NaOH 0,20 M à 50,0 ml d’une solution de HCl 0,10 M. La figure 6.3.3 (a) montre le pH observé en fonction du NaOH ajouté. Comme le HCl est un acide fort qui est complètement ionisé dans l’eau, le [H₃O+] initial est de 0,10 M, et le pH initial est de 1,00. L’ajout de NaOH diminue la concentration de H3O+ en raison de la réaction de neutralisation :

OH^– (aq) + H₃O⁺ (aq) → 2H₂O (l)

Ainsi, au fur et à mesure que l’on ajoute du NaOH, le HCl est consommé, et le pH de la solution augmente progressivement. Cependant, près du point d’équivalence, il ne reste plus qu’une petite fraction du HCl initialement présent, et le pH augmente donc beaucoup plus rapidement à mesure que chaque goutte de NaOH est ajoutée. Pour le titrage d’un acide fort monoprotique (HCl) avec une base forte monobasique (NaOH), nous pouvons calculer le volume de base nécessaire pour atteindre le point d’équivalence à partir de la relation suivante :

moles d’acide = moles de base

C_acide x V_acide = C_base x V_base

Dans notre titrage, 50,0 ml d’une solution 0,10 M de HCl, sont titrés avec du NaOH 0,20 M. Nous pouvons donc résoudre pour V_base, le volume de base nécessaire pour atteindre le point d’équivalence :

V_base= (C_acide x V_acide ) / C_base = 0.0250 L = 25.0 mL

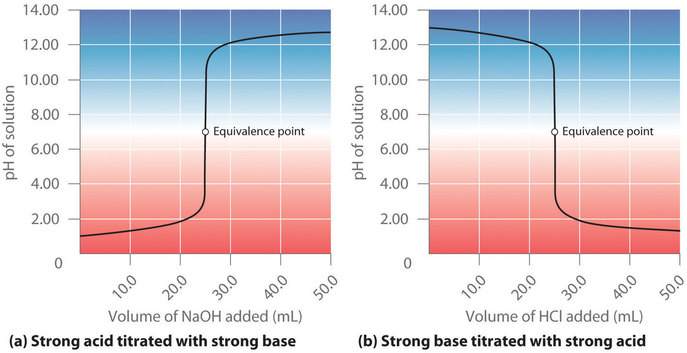
Figure 6.3.3. Le titrage (a) d’un acide fort avec une base forte et (b) d’une base forte avec un acide fort(a) Comme du NaOH 0,20 M est lentement ajouté à 50,0 ml de HCl 0,10 M, le pH augmente lentement au début, puis très rapidement à l’approche du point d’équivalence, et enfin augmente lentement une fois de plus. (b) Inversement, lorsque du HCl 0,20 M est lentement ajouté à 50,0 ml de NaOH 0,10 M, le pH diminue lentement au début, puis très rapidement à l’approche du point d’équivalence, et enfin diminue lentement une fois de plus.

Au point d’équivalence (lorsque 25,0 ml de solution de NaOH ont été ajoutés), la neutralisation est complète. Rappelons au chapitre 5 que toutes les réactions de neutralisation acide-base suivent l’équation générale

acide + base → sel + eau

Dans la réaction HCl + NaOH, le sel produit est du NaCl, qui ne s’hydrolyse pas et est donc un sel neutre. En général, les titrages d’un acide fort et d’une base forte donnent des sels neutres, et donc le pH de la solution au point d’équivalence est toujours de 7,00. Au-delà du point d’équivalence, l’ajout de NaOH supplémentaire produit une augmentation rapide du pH, mais le pH finit par s’éloigner de la valeur maximale, le pH de 0,20 M de NaOH.

Comme le montre la figure 6.3.3 (b), le titrage de 50,0 ml d’une solution de NaOH 0,10 M avec du HCl 0,20 M produit une courbe de titrage qui est presque l’image miroir de la courbe de titrage de la figure 6.3.2 (a). Le pH est initialement de 13,00, et il diminue lentement à mesure que l’on ajoute du HCl. À l’approche du point d’équivalence, le pH diminue rapidement avant de se stabiliser à une valeur d’environ 0,70, le pH de 0,20 M HCl.

En conclusion, les titrages d’acides forts avec des bases fortes (ou vice-versa) produisent une courbe en forme de S. La courbe n’est pas tout à fait parfaitement symétrique car l’augmentation constante du volume de la solution pendant le titrage entraîne une plus grande dilution de la solution. Comme les acides forts et les bases fortes s’ionisent complètement dans l’eau, la position et la forme exactes de la courbe ne dépendent que des concentrations de l’acide et de la base utilisés, et non de leur identité. Enfin, ces titrages produisent toujours des sels neutres, de sorte que la solution aqueuse obtenue au point d’équivalence a toujours un pH de 7.

Exemple 6.3.1 – Acide chlorhydrique

Calculer le pH de la solution après avoir ajouté 24,90 ml de NaOH 0,200 M à 50,00 ml de HCl 0,100 M.

Solution

Calculer le nombre de millimoles de H₃O⁺ et de OH- pour déterminer lequel, le cas échéant, est en excès après la réaction de neutralisation. Si une espèce est en excès, calculez la quantité qui reste après la réaction de neutralisation.

Comme 0,100 mol/L équivaut à 0,100 mmol/mL, le nombre de millimoles de H₃O⁺ dans 50,00 ml de HCl 0,100 M peut être calculé comme suit :

50.00 mL(0.100 mmol HCl/mL) = 5.00 mmol HCl= 5.00 mmol H₃O+

Le nombre de millimoles de NaOH ajoutées est le suivant :

24.90 mL(0.200 mmol NaOH/mL) =4.98 mmol NaOH =4.98 mmol OH-

Ainsi, le H₃O⁺ est en excès. Pour neutraliser complètement l’acide, il faut ajouter 5,00 mmol de OH- à la solution de HCl. Comme seulement 4,98 mmol de OH- ont été ajoutés, la quantité de H₃O⁺ en excès est de 5,00 mmol – 4,98 mmol = 0,02 mmol de H₃O⁺.

Déterminer le volume final de la solution. Calculer la concentration de l’espèce en excès et convertir cette valeur en pH.

Le volume final de la solution est de 50,00 ml + 24,90 ml = 74,90 ml, la concentration finale de H3O+ est donc la suivante :

[H+]= 0.02 mmol H+/ 74.90 mL= 3×10^-4 M

C’est pourquoi,

pH≈-log[H₃O⁺]=-log(3×10^-4)=3.5

Ce chiffre est nettement inférieur au pH de 7,00 pour une solution neutre.

Vérifiez votre apprentissage 6.3.1 – Acide chlorhydrique

Calculer le pH d’une solution préparée en ajoutant 40,00 ml de HCl 0,237 M à 75,00 ml d’une solution de NaOH 0,133 M.

Réponse

11.6

Titrages des acides et des bases faibles

Contrairement aux acides et aux bases fortes, la forme de la courbe de titrage d’un acide faible ou d’une base faible dépend fortement de l’identité de l’acide ou de la base et du K_a ou K_b correspondant. Comme nous le verrons, le pH change aussi beaucoup plus progressivement autour du point de demi-équivalence dans le titrage d’un acide faible ou d’une base faible. Comme vous l’avez appris précédemment, le [H₃O⁺] d’une solution d’acide faible (HA) n’est pas égal à la concentration de l’acide mais dépend à la fois de son K_a et de sa concentration. Comme seule une fraction d’un acide faible se dissocie, [H₃O⁺] est inférieur à [HA]. Ainsi, le pH d’une solution d’un acide faible est supérieur au pH d’une solution d’un acide fort de même concentration. La figure 6.3.4 (a) montre la courbe de titrage pour 50,0 ml d’une solution d’acide acétique 0,100 M avec du NaOH 0,200 M superposée à la courbe de titrage de HCl 0,100 M présentée dans la partie (a) de la figure 6.3.2.

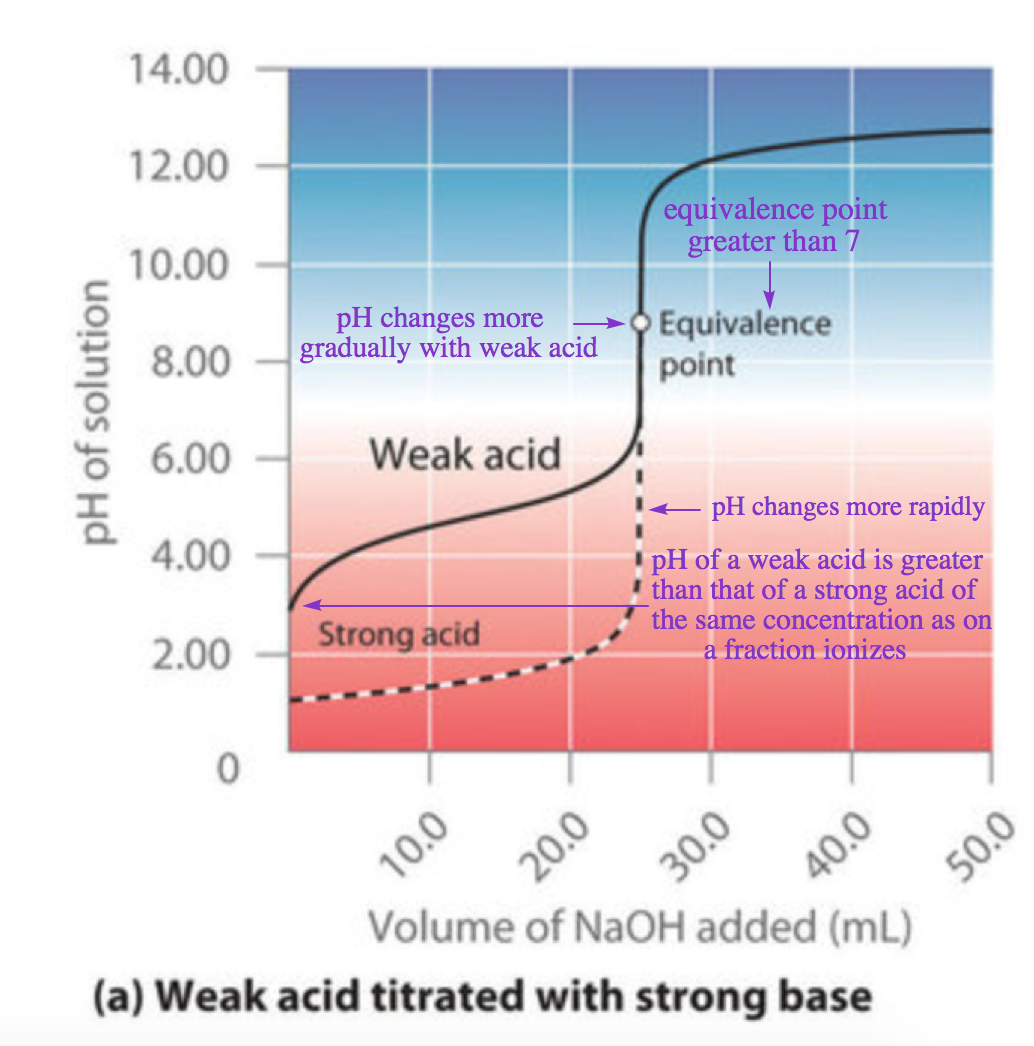
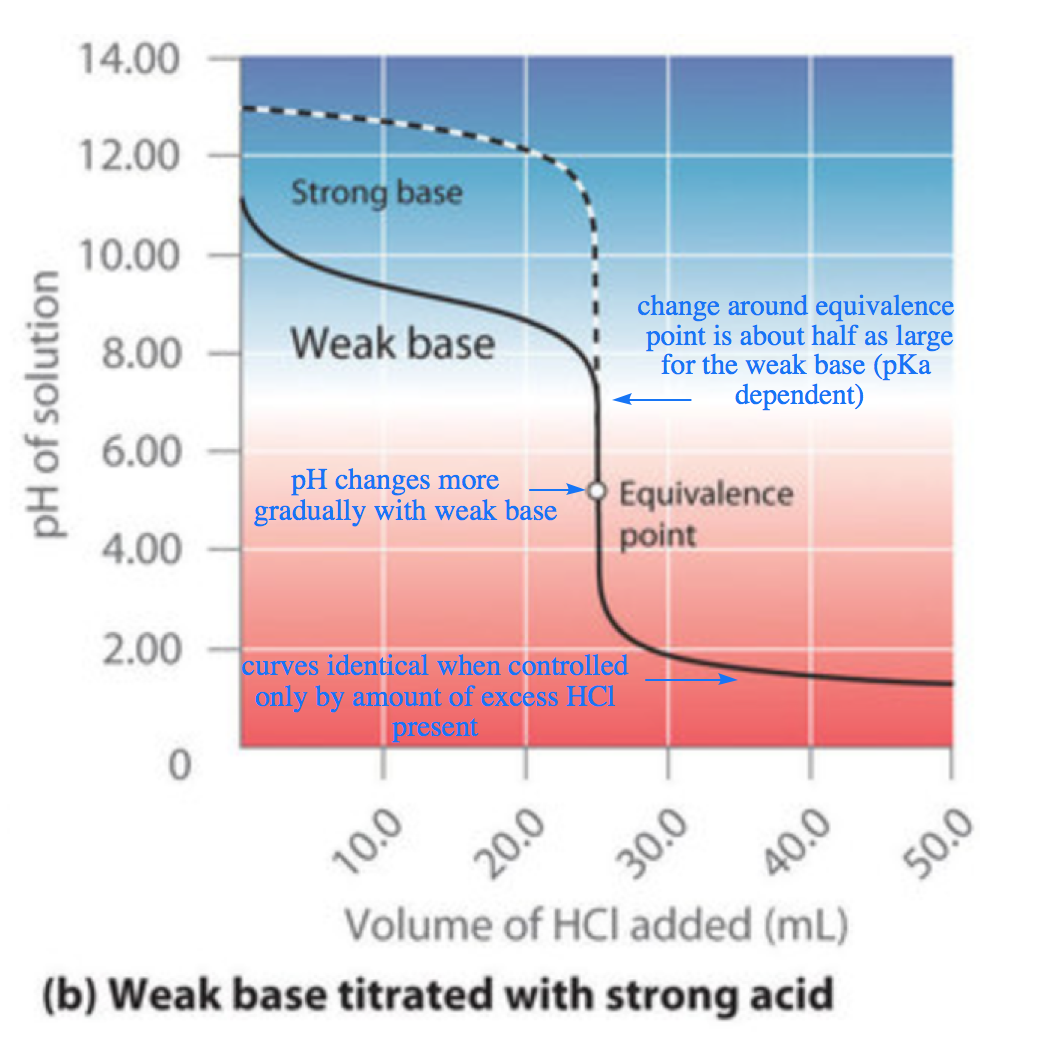
Figure 6.3.4. Le titrage de (a) un acide faible avec une base forte et (b) une base faible avec un acide fort. (a) En ajoutant lentement du NaOH 0,200 M à 50,0 ml d’acide acétique 0,100 M, le pH augmente d’abord lentement, puis rapidement à l’approche du point d’équivalence, et enfin plus lentement. La courbe correspondante pour le titrage de 50,0 ml de HCl 0,100 M avec du NaOH 0,200 M est représentée par une ligne pointillée. (b) Lorsque l’on ajoute lentement du HCl 0,200 M à 50,0 ml de NH3 0,100 M, le pH diminue d’abord lentement, puis rapidement à l’approche du point d’équivalence, et enfin il diminue à nouveau plus lentement. La courbe correspondante pour le titrage de 50,0 ml de NaOH 0,100 M avec du HCl 0,200 M est représentée par une ligne pointillée.

En dessous du point d’équivalence, les deux courbes sont très différentes. Tout d’abord, notez qu’avant l’ajout de toute base, le pH initial de la solution d’acide acétique est supérieur au pH initial de la solution de HCl, ceci est dû au fait que l’acide acétique est un acide faible et qu’il ne s’ionise donc pas complètement en solution. Deuxièmement, notez que les courbes entre le point initial et le point d’équivalence ont des formes différentes : pour le titrage de l’acide acétique, le pH change plus rapidement au début, se stabilise légèrement, puis recommence à augmenter à mesure que l’on s’approche du point d’équivalence. Enfin, notez également que le pH de la solution au point d’équivalence est supérieur à 7,00, c’est-à-dire que la solution est basique. Au-delà du point d’équivalence, cependant, les deux courbes sont identiques : une fois l’acide neutralisé, le pH de la solution est contrôlé uniquement par la quantité de NaOH en excès, que l’acide soit faible ou fort.

N’examinons pas de manière plus quantitative la construction des courbes de titrage. La courbe de la figure 6.3.4 (a) a été créée en calculant le pH de départ de la solution d’acide acétique avant l’ajout de NaOH, puis en calculant le pH de la solution après l’ajout de volumes croissants de NaOH. Dans la sous-section suivante, nous allons passer en revue ces calculs pour trois points de la courbe, en utilisant le pKa de l’acide acétique (4,74 à 25°C).

Calcul du pH initial d’une titration

Comme nous l’avons vu précédemment, si nous connaissons le K_a ou le K_b et la concentration initiale d’un acide faible ou d’une base faible, respectivement, nous pouvons calculer le pH d’une solution d’un acide faible ou d’une base faible en établissant un tableau ICE. Dans cette situation, la concentration initiale d’acide acétique est de 0,100 M. Si nous définissons x comme [H₃O⁺], le tableau des concentrations pour l’ionisation de l’acide acétique 0,100 M est le suivant :

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

*Remarque : dans cet exemple et tous les suivants, nous ne tiendrons pas compte des [H₃O⁺] et [OH^–] dus à l’autoionisation de l’eau, car ces quantités seront négligeables.

Insérer les expressions des concentrations finales dans l’équation d’équilibre (et utiliser des approximations),

K_a=([H₃O⁺][CH₃CO^2-])/[CH₃CO₂H]=x²/(0.100-x)≈x²/0.100=1.8×10^-5

La résolution de cette équation donne x = [H₃O+] = 1,32 × 10-3 M. Le pH d’une solution d’acide acétique à 0,100 M est donc le suivant :

pH= -log(1.32×10^-3) = 2.879

C’est le pH initial de notre courbe de titrage (c’est-à-dire l‘ordonnée à l’origine, où le volume de base ajoutée est de 0 ml).

Calcul du pH pendant le titrage

Considérons maintenant ce qui se passe lorsque nous ajoutons 5,00 ml de NaOH 0,200 M à 50,00 ml de CH3CO2H 0,100 M (toujours selon la figure 6.3.3 (a)). Comme la réaction de neutralisation se poursuit jusqu’à son terme, tous les ions OH- ajoutés réagiront avec l’acide acétique pour générer de l’ion acétate et de l’eau :

CH3CO2H (aq) + OH- (aq) → CH3CO2- (aq) + H2O (l)

Tous les problèmes de ce type doivent être résolus en deux étapes : un calcul stœchiométrique suivi d’un calcul d’équilibre. Dans la première étape, nous utilisons la stœchiométrie de la réaction de neutralisation pour calculer les quantités d’acide et de base conjuguée présentes en solution après que la réaction de neutralisation a eu lieu. Dans la deuxième étape, nous utilisons l’équation d’équilibre pour déterminer [H₃O⁺] de la solution résultante.

Étape 1 – La stœchiométrie d’abord

Pour déterminer la quantité d’acide et de base conjuguée en solution après la réaction de neutralisation, nous calculons la quantité de CH3CO2H dans la solution d’origine et la quantité de OH- dans la solution de NaOH qui a été ajoutée. La solution d’acide acétique contenait à l’origine

50.00mL⋅(0.100 mmol CH₃CO₂H/mL)=5.00mmol CH₃CO₂H

La solution de NaOH ajoutée contenait 5,00 ml x 0,200 mmol de NaOH/mL = 1,00 mmol de NaOH

La comparaison de ces deux montants montre que le CH₃CO₂H est en excès. Comme OH- réagit avec le CH₃CO₂H selon une stœchiométrie 1:1, la quantité de CH3CO2H en excès est la suivante :

5.00 mmol CH₃CO₂H – 1.00 mmol OH- =4.00 mmol CH₃CO₂H

Chaque mmol de OH- réagit pour produire 1 mmol d’ion acétate, de sorte que la quantité finale de CH3CO2- est de 1,00 mmol.

La stœchiométrie de la réaction est résumée dans le tableau suivant, souvent appelé tableau BAMA ou tableau de stœchiométrie, qui indique le nombre de moles des différentes espèces et les changements qui en résultent à la suite d’une réaction qui se déroule à 100 % :

Remarque : les tableaux ICE permettent de suivre l’évolution des concentrations ou des pressions dans un problème d’équilibre. Il ne s’agit pas d’un tableau ICE, car il s’agit d’une réaction à sens unique qui se répercute à 100 % sur les produits, et le calcul est donc un problème de type réactif limite.

Le tableau BAMA indique que la quantité initiale d’acétate et la quantité finale d’ions OH- sont égales à 0. Cependant, comme une solution aqueuse d’acide acétique contient toujours au moins une petite quantité d’ions acétate en équilibre avec l’acide acétique, la concentration initiale d’acétate n’est pas réellement égale à 0. Cette valeur peut être ignorée dans ce calcul car la quantité de CH₃CO₂^– en équilibre est insignifiante par rapport à la quantité d’OH- ajoutée. En outre, en raison de l’autoionisation de l’eau, aucune solution aqueuse ne peut contenir 0 mmol de OH-, mais la quantité de OH^– due à l’autoionisation de l’eau est également insignifiante par rapport à la quantité de OH- ajoutée. Nous utilisons les quantités initiales des réactifs pour déterminer la stœchiométrie de la réaction et reportons la prise en compte de l’équilibre à la seconde moitié du problème.

Étape 2 – Maintenant, activez l’équilibre acide-base

Pour calculer [H₃O⁺] à l’équilibre après l’addition de NaOH, nous devons d’abord recalculer [CH₃CO₂H] et [CH₃CO₂^–] en utilisant le nombre de millimoles de chacun et le volume total de la solution à ce point du titrage :

total volume = 50.00 mL + 5.00 mL= 55.00 mL

[CH₃CO₂H] = 4.00 mmol CH₃CO₂H / 55.00mL= 7.27×10^-2 M

[CH₃CO₂^–] =1.00mmol CH₃CO₂^–  / 55.00mL = 1.82×10^-2 M

En connaissant les concentrations d’acide acétique et d’ion acétate à l’équilibre et le Ka de l’acide acétique (1,74 × 10^-5), nous pouvons calculer [H₃O⁺] à l’équilibre :

K_a= ([CH₃CO₂^–][H₃O⁺])/[CH₃CO₂H]

[H₃O⁺] = K_a x ([CH₃CO₂H]/[CH₃CO₂^–]) = (1.72×10-5) x (7.27×10-2M)/(1.82×10-2) =6.95×10^-5 M

Calculer -log [H₃O⁺] donne

pH= -log(6.95×10^-5) = 4.158

En comparant les courbes de titrage pour le HCl et l’acide acétique dans la figure 6.3.4 (a), nous voyons que l’ajout de la même quantité (5,00 ml) de NaOH 0,200 M à 50 ml d’une solution 0,100 M des deux acides provoque une variation de pH beaucoup plus faible pour le HCl (de 1,00 à 1,14) que pour l’acide acétique (2,88 à 4,16). Ceci est conforme à la description qualitative des formes des courbes de titrage au début de cette section. Répétons maintenant le processus ci-dessus pour un autre point de la courbe de titrage de l’acide acétique.

Exemple 6.3.2 – Calcul du pH au point d’équivalence du titrage

Quel est le pH de la solution après avoir ajouté 25,00 ml de NaOH 0,200 M à 50,00 ml d’acide acétique 0,100 M ?

Solution

En ignorant l’ion du spectateur (Na⁺), l’équation pour la neutralisation est toujours: :

CH₃CO₂H (aq) + OH⁻ (aq) → CH₃CO₂⁻ (aq) + H₂O (l)

Le nombre de millimoles de OH^– ajoutées après 25,00 ml est :

25.00mL⋅(0.200 mmol OH^–/mL)= 5.00 mmol OH^–

Comme le titrage a commencé avec exactement 5,00 mmol de CH3CO2H, le nombre de millimoles de OH- ajouté est égal au nombre de millimoles de CH3CO2H, aucune espèce n’est présente en excès, et nous avons donc atteint le point d’équivalence. Là encore, les résultats de la réaction de neutralisation peuvent être résumés dans un tableau BAMA (stœchiométrie) :

Au point d’équivalence, les 5,00 millimoles de CH₃CO₂H ont été convertis en sa base conjuguée, CH₃CO₂⁻; cependant, le nouveau volume total de la solution est de 75,00 ml (50,00 + 25,00 ml), et donc sa concentration :

[CH₃CO₂⁻] = 5.00 mmol CH₃CO₂⁻ / (50.00+25.00) mL = 6.67×10^-2 M

Quel est le pH de cette solution d’acétate ? L’acétate est une base, et va donc s’hydrolyser en solution pour reformer un peu d’acide acétique, à l’équilibre :

CH₃CO₂⁻ (aq) + H₂O (l) ⇌ CH₃CO₂H (aq) + OH⁻ (aq)

Par conséquent, nous devons considérer la réaction de la base conjuguée avec l’eau pour calculer [H3O+] à l’équilibre et donc le pH final de la solution, en utilisant une table ICE :

CH₃CO₂⁻ (aq) + H₂O (l) ⇌ CH₃CO₂H (aq) + OH⁻ (aq)

Substitution des valeurs de ce tableau dans l’équation Kb,

K_b =K_w/K_a = (1.01×10^-14)/(1.74×10^-5) = 5.80×10^-10= x²/0.0667

nous pouvons le résoudre pour obtenir x = 6,22 × 10^-6. Ainsi, à l’équilibre, [OH^–] = 6,22 × 10^-6 M, et le pH de la solution finale est de 8,794 (figure 6.3.4 (a)). Comme prévu pour le titrage d’un acide faible, le pH au point d’équivalence est supérieur à 7,00 parce que le produit du titrage est une base, l’ion acétate, qui s’hydrolyse ensuite pour produire OH^–.

Vérifiez votre apprentissage 6.3.2 – Calcul du pH au point d’équivalence du titrage

125,0 ml d’une solution d’ammoniac 0,150 M sont titrés avec 45,0 ml d’une solution de HCl 0,213 M. (a) Ce titrage est-il avant, après ou au point d’équivalence ? (b) Calculer le pH de la solution. Le pK_b de l’ammoniac est de 4,75 à 25°C.

Réponse

Avant le point d’équivalence ; (b) 9.23

Comme le montre la figure 6.3.3 (b), la courbe de titrage du NH₃, une base faible, est l’inverse de celle de l’acide acétique. Notez en particulier que le pH au point d’équivalence dans le titrage d’une base faible est inférieur à 7,00 parce que le titrage produit un acide.

Comme nous l’avons vu précédemment, les courbes de titrage des acides forts et des bases fortes sont des courbes en S presque symétriques, où seule la concentration, mais pas l’identité, de l’espèce est pertinente. Cependant, dans les titrages d’acides faibles ou de bases faibles, l’identité de l’acide faible ou de la base faible titrée affecte fortement la forme de la courbe de titrage. Lorsque l’acide ou la base titrée devient plus faible (son pKa ou _pKb augmente), la variation du pH autour du point d’équivalence diminue de manière significative. Avec des solutions très diluées, la courbe devient si peu profonde qu’elle ne peut plus être utilisée pour déterminer le point d’équivalence.

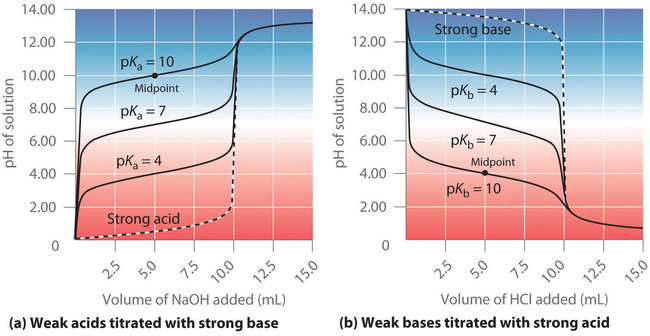
Figure 6.3.5. Effet de la force acide ou basique sur la forme des courbes de titrage. Contrairement aux acides ou aux bases forts, la forme de la courbe de titrage d’un acide ou d’une base faible dépend du pKa ou du pKb de l’acide ou de la base faible titré. a) pH de la solution en fonction du volume de NaOH 1,00 M ajouté à 10,00 ml de solutions 1,00 M d’acides faibles ayant les valeurs de pKa indiquées. b) pH de la solution en fonction du volume de HCl 1,00 M ajouté à 10,00 ml de solutions 1,00 M de bases faibles ayant les valeurs de pK_b indiquées. Les points médians sont indiqués pour les courbes de titrage correspondant à pK_a = 10 et pK_b = 10.

Un point dans le titrage d’un acide faible ou d’une base faible est particulièrement important : le point médian (ou point de demi-équivalence) d’un titrage est défini comme le point auquel on a ajouté exactement assez d’acide (ou de base) pour neutraliser la moitié de l’acide (ou de la base) présent à l’origine et qui se situe à mi-chemin du point d’équivalence. Le point médian est indiqué dans la figure 6.3.5 pour les deux courbes les plus faibles. Par définition, au point médian du titrage d’un acide, [HA] = [A^–]. Rappelons que la constante d’ionisation pour un acide faible est la suivante :

K_a=([H₃O⁺][A^–])/[HA]

Équation 6.3.1. Constante d’ionisation pour l’acide faible

Si [HA] = [A^–], cela se réduit à K_a = [H₃O⁺]. En prenant le logarithme négatif des deux côtés,

-log(K_a) = -log[H₃O⁺]

D’après les définitions du pKa et du pH, nous constatons qu’il est identique à

pK_a=pH

Ainsi, le pH au point médian du titrage d’un acide faible est égal au pKa de l’acide faible. Dans la figure 6.3.4 (a), on peut voir que le point médian pour le pKa = 10 de l’acide faible se produit à pH = 10. Les méthodes de titrage peuvent donc être utilisées pour déterminer à la fois la concentration et le pKa (ou le pKb) d’un acide faible (ou d’une base faible).

Titrages d’acides ou de bases polyprotiques

Lorsqu’une base forte est ajoutée à une solution d’un acide polyprotique, la réaction de neutralisation se produit par étapes. Le proton le plus acide est titré en premier, suivi par le suivant le plus acide, et ainsi de suite. Si les valeurs de pKa sont séparées par au moins trois unités de pH, la courbe de titrage globale présente des “étapes” bien résolues correspondant au titrage de chaque proton. Par exemple, le titrage de l’acide triprotique H3PO4 avec du NaOH est illustré sur la figure 6.3.6 et présente deux étapes bien définies : le premier point médian correspond au pKa1, et le second point médian correspond au pKa2. Comme l’HPO₄^2- est un acide très faible, le pKa3 a une valeur si élevée que la troisième étape ne peut être résolue en utilisant du NaOH 0,100 M comme réactif de titrage.

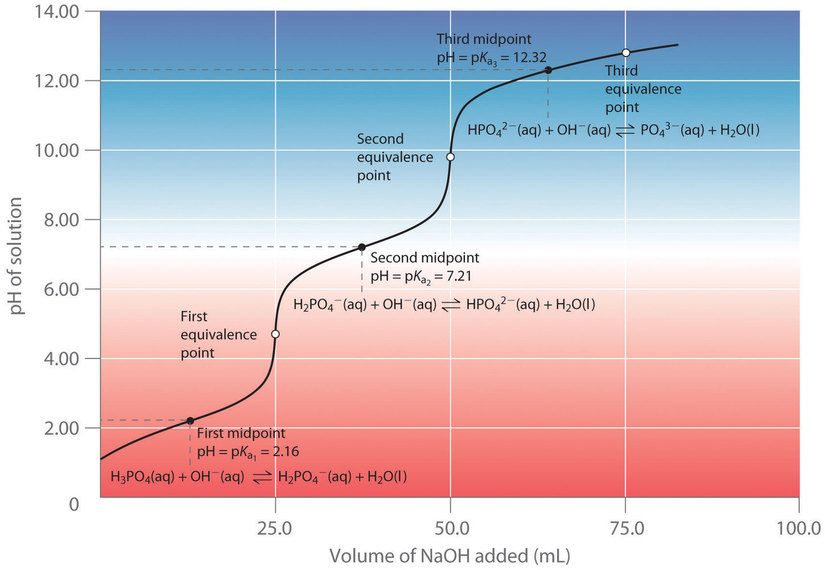
Figure 6.3.6. Courbe de titrage pour l’acide phosphorique (H3PO4), un acide polyprotique typique. La courbe pour le titrage de 25,0 ml d’une solution de H₃PO₄ 0,100 M avec du NaOH 0,100 M ainsi que les espèces en solution à chaque K_a est présentée. Notez les deux points d’équivalence distincts correspondant à la déprotonation de H₃PO₄ au pH ≈ 4,6 et de H₂PO₄^2- au pH ≈ 9,8. Comme le HPO₄^2- est un acide très faible, le troisième point d’équivalence, au pH ≈ 13, n’est pas bien défini.

La courbe de titrage pour la réaction d’une base polyprotique avec un acide fort est l’image miroir de la courbe présentée à la figure 6.3.6. Le pH initial est élevé, mais au fur et à mesure que l’on ajoute de l’acide, le pH diminue par étapes si les valeurs successives de pK_b sont bien séparées.

Titrage de l’acide diprotique

Calculer le pH d’une solution préparée en ajoutant 55,0 ml d’une solution de NaOH 0,120 M à 100,0 ml d’une solution d’acide oxalique (HO₂CCO₂H) 0,0510 M, un acide diprotique (abrégé en H2A). L’acide oxalique, l’acide dicarboxylique le plus simple, se trouve dans la rhubarbe et dans de nombreuses autres plantes. Les feuilles de rhubarbe sont toxiques car elles contiennent le sel de calcium de la forme entièrement déprotonée de l’acide oxalique, l’ion oxalate (-O₂CCO_2-, abrégé A^2-). Les sels d’oxalate sont toxiques pour deux raisons. Premièrement, les sels d’oxalate de cations divalents tels que Ca²⁺ sont insolubles à pH neutre mais solubles à faible pH. Par conséquent, l’oxalate de calcium se dissout dans l’acide dilué de l’estomac, ce qui permet à l’oxalate d’être absorbé et transporté dans les cellules, où il peut réagir avec le calcium pour former de minuscules cristaux d’oxalate de calcium qui endommagent les tissus. Deuxièmement, l’oxalate forme des complexes stables avec les ions métalliques, qui peuvent modifier la répartition des ions métalliques dans les fluides biologiques.

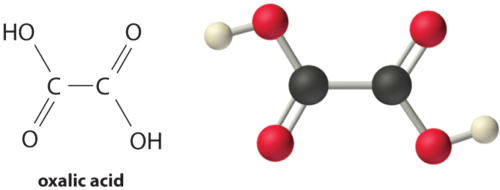
Les valeurs du pKa de l’acide oxalique sont de 1,25 et 3,81. On procède en déterminant les millimoles d’acide et de base initialement présentes :

100.00mL(0.510mmol H₂A / mL) =5.10 mmol H₂A

55.00 mL(0.120mmol NaOH / mL) = 6.60 mmol NaOH

L’acide le plus fort (H₂A) réagit d’abord avec la base. Cela laisse (6,60 – 5,10) = 1,50 mmol de OH^– pour réagir avec HA^–, formant A^2- et H₂O. Les réactions peuvent s’écrire comme suit :

H₂A + OH- → HA^– + H₂O

5,10 mmol 6,60 mmol 5,10 mmol 5,10 mmol

HA^– + OH- → A^2- + H₂O

5,10 mmol 6,60 mmol 5,10 mmol 5,10 mmol

Représenté sous forme de deux tableaux de stœchiométrie séquentielle :

L’équilibre entre l’acide faible (HA^–) et sa base conjuguée (A^2-) dans la solution finale est déterminé par l’amplitude de la seconde constante d’ionisation, K_a2 = 10-3,81 = 1,6 × 10-4. Pour calculer le pH de la solution, nous avons besoin de connaître [H₃O⁺], qui est déterminé en trouvant d’abord les concentrations de chaque espèce :

final volume of solution = 100.0mL + 55.0mL=  155.0mL

[HA^–] = 3.60mmol HA^– / 155.0mL= 2.32×10^-2 M

[A^2-] = 1.50mmol / 155.0mL= 9.68×10^-3 M

Nous pouvons maintenant calculer [H₃O⁺] à l’équilibre en utilisant l’expression _{Ka2 :}

K_a2= ([A^2-][H₃O⁺])/[HA^–]

Réorganiser cette équation et substituer les valeurs des concentrations de HA- et ^A2-,

[H₃O⁺] = K_a2([HA^–]/[A^2-]) = (1.6×10-4)((2.32×10-2)/(9.68×10-3)) =3.7×10^-4 M

Donc

pH=-log[H₃O⁺]=-log(3.7×10^-4)=3.43

Cette réponse est logique du point de vue chimique, car le pH se situe entre la première et la deuxième valeur du pK_a de l’acide oxalique, comme il se doit. Nous avons ajouté suffisamment d’ions hydroxyde pour titrer complètement le premier proton, plus acide (ce qui devrait nous donner un pH supérieur au pK_a1), mais nous n’en avons ajouté que suffisamment pour titrer moins de la moitié du second proton, moins acide, avec le pK_a2. Si nous avions ajouté exactement assez d’hydroxyde pour titrer complètement le premier proton plus la moitié du second, nous serions à mi-chemin de la deuxième étape du titrage, et le pH serait de 3,81, égal au pK_a2.

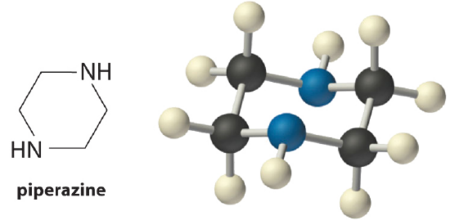
Vérifiez votre apprentissage (Piperazine) 6.3.3 – Titrage de l’acide diprotique

La pipérazine est une base diprotique utilisée pour contrôler les parasites intestinaux (“vers”) chez les animaux de compagnie et les humains. Un chien reçoit 500 mg (5,80 mmol) de pipérazine (pK_b1 = 4,27, pK_b2 = 8,67). Si l’estomac du chien contient initialement 100 ml de HCl 0,10 M (pH = 1,00), calculer le pH du contenu de l’estomac après l’ingestion de la pipérazine.

Réponse

pH = 4,9