6.1 – Effet de l’ion

L’effet de l’ion commun est utilisé pour décrire l’effet sur un équilibre existant par l’ajout d’une deuxième substance qui contient un ion commun à l’équilibre. Si plusieurs sels sont présents dans un système, ils s’ionisent tous dans la solution. Si les sels contiennent un cation ou un anion commun, ces sels contribuent à la concentration de l’ion commun. Les contributions de tous les sels doivent être incluses dans le calcul de la concentration de l’ion commun.

Ions communs

Lorsque NaCl et KCl, deux sels très solubles, sont dissous dans la même solution, les ions Cl^– sont communs aux deux sels. Dans un système contenant du NaCl et du KCl, les ions Cl^– sont des ions communs.

NaCl (s) → Na⁺ (aq) + Cl^– (aq)

KCl (s) → K⁺ (aq) + Cl^– (aq)

Comme les deux sels s’ionisent complètement en solution, nous pouvons utiliser la stœchiométrie pour exprimer les concentrations des ions dissous en solution dans l’équation suivante :

[Na⁺] + [K⁺] = [Cl^–]

Vous pouvez reconnaître l’équivalence ci-dessus comme une application des concepts de bilan de charge et de bilan de masse.

Exemple 6.1.1 – Concentrations d’ions communs

Que sont [Na⁺], [Cl^–], [Ca²⁺], et [H⁺],  dans une solution contenant 0,10 M de NaCl, CaCl₂ et HCl ?

Solution

Ces trois espèces s’ionisent complètement dans l’eau :

NaCl (s) → Na⁺ (aq) + Cl^– (aq)

KCl (s) → K⁺ (aq) + Cl^– (aq)

CaCl₂ (s) → Ca²⁺ (aq) + 2Cl^– (aq)

En utilisant la stœchiométrie, nous voyons que chaque mole de composé dissous produit une mole de cations. Par conséquent, en raison de la conservation des ions, nous avons :

[Na⁺] = [Ca²⁺] = [H₃O⁺] = 0.10 M

Chaque composé produit des ions chlorure ; cependant, on note que le chlorure de calcium produit 2 moles d’ions Cl^– pour chaque mole de CaCl₂ dissous. Par conséquent, la quantité totale d’ions chlorure en solution est de

[Cl^–] = 0,10 (dû au NaCl) + 0,20 (dû au CaCl₂) + 0,10 (dû au HCl) M

= 0.40 M

Exemple 6.1.2 – Calculs des ions communs

John a versé 10,0 ml de solutions de NaCl 0,10 M, 10,0 ml de KOH 0,10 M et 5,0 ml de HCl 0,20 M ensemble, puis il a fait en sorte que le volume total soit de 100,0 ml. Que contient [Cl-] dans la solution finale ?

Solution

[Cl^–] =(0.1M×10mL+0.2M×5.0mL)/100.0mL=0.020M

Effet des ions communs et équilibres

Dans les exemples ci-dessus, comme tous les composés sont ionisés à 100 %, nous pourrions utiliser la stœchiométrie simple pour trouver les concentrations de l’ion commun. Mais que se passe-t-il si nous impliquons des substances qui ne s’ionisent que partiellement en solution ? Quel serait l’effet d’un ion commun sur un équilibre ?

Le principe de Le Châtelier stipule que si un équilibre devient déséquilibré, la réaction se déplacera afin de rétablir l’équilibre. Considérons l’équation chimique suivante, représentant l’ionisation d’un acide faible générique :

HA + H₂O ←> H₃O⁺ + A^–

Si nous ajoutions une deuxième substance, par exemple le sel de sodium de la base conjuguée (NaA) à cette solution, ce sel soluble augmenterait la concentration de l’ion A- en solution :

NaA (s) → Na⁺ (aq) + A^– (aq)

L’ion A- est l’ion commun aux deux équations chimiques, mais notez leurs différences : le premier est un équilibre, mais le second va jusqu’au bout. Ainsi, la présence du sel de sodium augmente la concentration de la base conjuguée. Selon le Principe de Le Chatelier, une augmentation de [A-] signifie que l’équilibre acide faible se déplacera vers les réactifs.

En général, on peut conclure que l’ajout d’un ion commun empêche un acide faible (ou de même, une base faible) de s’ioniser autant qu’il le ferait sans l’ion commun ajouté. L’effet de l’ion commun supprime l’ionisation d’un acide faible par l’ajout d’un ion qui est un produit de cet équilibre. L’ajout d’un ion commun à un système à l’équilibre affecte la composition de l’équilibre, mais pas la constante d’ionisation. L’exemple ci-dessous, impliquant la dissolution d’un sel légèrement soluble, illustre ce concept important.

Exemple 6.1.3 – Ion commun ajouté à un système à l’équilibre

L’hydroxyde de calcium est un sel peu soluble qui existe en équilibre en solution aqueuse avec ses ions. Une solution de Ca(OH)₂ à l’équilibre contient [Ca2+] = 0,0108 M, [OH-] = 0,0216 M, et un peu de sel solide. À cette solution, vous ajoutez du chlorure de calcium solide, qui s’ionise complètement en Ca2+ et Cl- et permet au système de rétablir l’équilibre. Lorsque vous mesurez à nouveau les concentrations d’ions, vous constatez que la solution contient maintenant [Ca2+] = 0,0374 M et [OH-] = 0,0116 M. Calculez la constante d’équilibre pour la dissolution de l’hydroxyde de calcium avant et après l’ajout de chlorure de calcium, en arrondissant à 2 chiffres significatifs. Que pouvez-vous conclure lorsque vous comparez ces valeurs ?

Solution

Tout d’abord, écrivez l’équation chimique de la dissolution de l’hydroxyde de calcium à l’équilibre :

Ca(OH)₂ (s) ⇌ Ca²⁺ (aq) + 2OH^– (aq)

L’expression de la constante d’équilibre pour l’équilibre ci-dessus est :

K = [Ca²⁺][OH^–]²

En substituant les concentrations d’ions calcium et hydroxyde présents à l’équilibre avant l’ajout de chlorure de calcium, on obtient :

K = (0.0108)(0.0216)²

K = 5.0×10^–6

Maintenant, nous recalculons K en utilisant les concentrations après l‘ajout du sel contenant l’ion commun :

K = (0.0374)(0.0116)²

K = 5.0×10^–6

En comparant ces valeurs, nous pouvons conclure que, si les concentrations d’équilibre des ions changent, la valeur de la constante d’équilibre elle-même ne change pas avec l’ajout d’un ion commun.

Pour en revenir à notre discussion sur les acides faibles, nous savons maintenant que la présence d’un ion commun supprime l’ionisation de l’acide faible, diminuant les concentrations des ions produits, mais n’affecte pas la constante d’équilibre, K_a. Ceci est illustré ci-dessous dans la figure 6.1.1 : l’ajout d’un acide fort, tel que HCl, à une solution d’un acide faible déplace l’équilibre vers les réactifs. Le HCl s’ionise complètement, augmentant la concentration de H₃O⁺, qui supprime alors l’ionisation de l’acide faible présent, l’acide acétique.

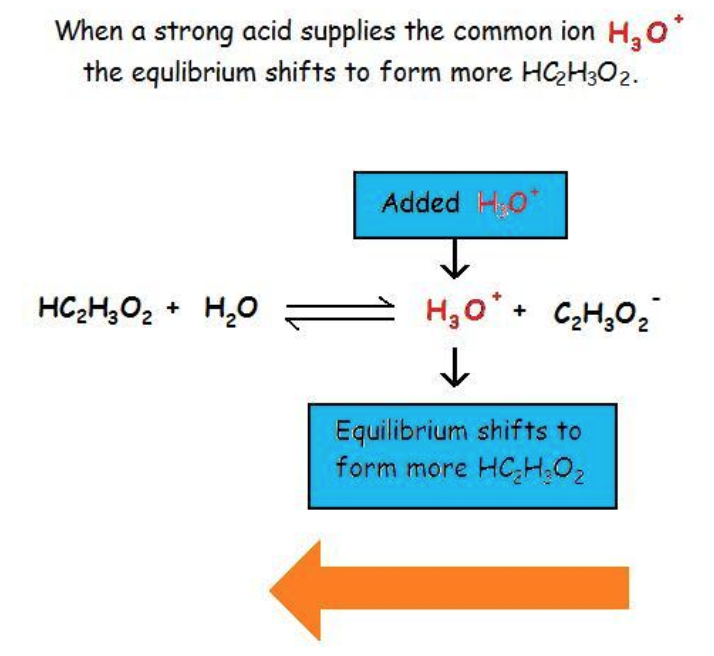
Figure 6.1.1. L’ajout d’un acide fort (par exemple HCl) à une solution d’acide acétique (un acide faible) déplace l’équilibre vers les réactifs, inhibant ainsi l’ionisation de l’acide faible.

L’effet ion commun supprime également l’ionisation d’une base faible en augmentant à nouveau la concentration d’un ion produit de l’équilibre. Par exemple, la figure 6.1.2 montre l’effet de l’ion commun de l’addition de OH^– (provenant d’une base forte) sur l’ionisation de l’ammoniac, une base faible :

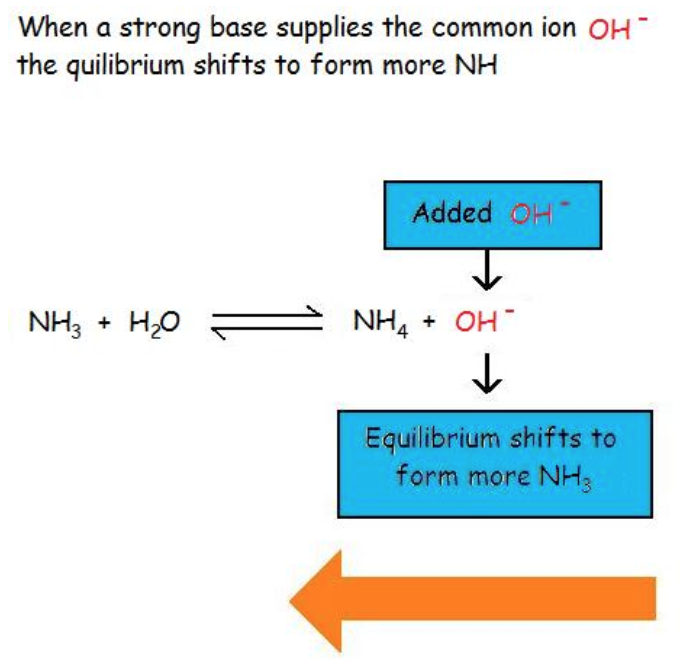
Figure 6.1.2. L’ajout d’une base forte (par exemple NaOH) à une solution d’ammoniac (une base faible) déplace l’équilibre vers les réactifs, inhibant ainsi l’ionisation de la base faible.

L’ajout d’une base forte telle que le NaOH, entraîne une augmentation de la concentration de l’ion commun de l’hydroxyde, et donc une augmentation du quotient de réaction, Q :

Q=([NH₄⁺][OH^–])/[NH₃]

Q > K, et donc le système n’est plus à l’équilibre. Pour rétablir l’équilibre, la valeur de Q doit être diminuée en diminuant la quantité de produits et en augmentant la quantité de réactif. Par conséquent, la réaction se déplace vers la gauche pour contrebalancer le déséquilibre (conformément au principe de Le Châtelier), formant ainsi davantage de réactifs. Cela diminue Q jusqu’à ce qu’il soit égal à la constante d’équilibre, K_b = 1,8 x 10^-5, et un nouveau point d’équilibre est atteint. Exemple

Exemple 6.1.4 – Ion commun ajouté à un système à l’équilibre

Quel est le pH d’une solution de HOCl à 0,100 M ? Quel est le pH d’une solution qui contient à la fois 0,100 M de HOCl et 0,010 HCl ? Que pouvez-vous conclure en comparant ces deux valeurs ?

Solution

Le HOCl est un acide faible, avec K_a = 4,0×10^-8. Nous utilisons un tableau ICE pour trouver la concentration en ions hydronium à l’équilibre et ensuite le pH :

HOCl + H₂O⇌ H₃O⁺ + OCl^–

K_a=4.0×10^-8=([H₃O⁺(aq)][OCl^–])/[HOCl]

=x²/(0.100-x)

x = 6.3×10^–5 M = [H₃O⁺]

pH = 4.20

Maintenant, nous répétons ce calcul, mais cette fois en tenant compte des 0,010 M H3O+ formés par l’ionisation complète de l’acide fort, HCl :

HOCl + H₂O⇌ H₃O⁺ + OCl^–

K_a=4.0×10^-8=([H₃O⁺(aq)][OCl^–])/[HOCl]

=((0.010+x)(x))/0.100-x

x = 4.0×10^–7 M

[H₃O⁺] = 0.010 + x = 0.010 M + 4.0×10^–7 M = 0.010 M

pH = 2.00

Dans les deux cas, nous avons fait l’hypothèse que “x est petit” pour simplifier le calcul (la vérification du résultat confirme que cette hypothèse est valable). En comparant les deux résultats, nous constatons que dans le second cas, près de 100 % de l’ion hydronium à l’équilibre provient de la source d’acide fort, HCl. En présence de l’acide fort, très peu de l’HOCl s’ionise, ce qui illustre l’effet de l’ion commun sur cet équilibre.

Vérifiez votre apprentissage 6.1.4 – Ion commun ajouté à un système à l’équilibre

Quel est le pH d’une solution de 0,150 M NH₃ et de 0,045 M NH₄Cl ?

Réponse

9.78

Questions

★ Questions

1. Le produit de solubilité Ksp du sulfure de bismuth Bi₂S₃ est de 1,6 x 10^-72 à 25°C. Quelle est la solubilité molaire du sulfure de bismuth dans une solution qui est de 0,0010 M dans le sulfure de sodium Na₂S ?
2. John a versé 1,0 ml de solutions de NaCl 0,10 M, 1,0 ml de KOH 0,10 M et 1,0 ml de HCl 0,20 ensemble, puis il a fait en sorte que le volume total soit de 100,0 ml. Quelle est la teneur en [Cl^–] de la solution finale (g⋅mol^-1) ?
3. Le K_sp pour l’AgCl est de 1,0 x 10^-10. De laquelle des solutions suivantes le chlorure d’argent précipiterait-il ?

A. Une solution 0,10 M Ag+ et 1,00 M Cl-

B. Une solution 1,0 x 10^-5 M en Ag⁺ et 0,20 M en Cl^–

C. Une solution 1,0 x 10^-7 M en Ag⁺ et 10^-7 M en Cl-

4. Parmi les substances suivantes, laquelle provoque la précipitation d’un sel à partir d’un litre d’une solution de Mg²⁺ 1 x 10^-4 M ?

A. 1 x 10^-4 mole NaOH

B. 1 x 10^-1 mole d’acide nitrique

C. 1 x 10^-5 mole d’acétate de potassium

D. 1 x 10^-4 mole de nitrate d’ammonium

E. 1 x 10^-2 mole de fluorure de sodium

5. Le K_sp pour le chromate de strontium est de 3,5 x 10^-5 et le K_sp pour le chromate de baryum est de 1,2 x 10^-10. Quelle concentration de chromate de potassium précipitera la quantité maximale de chromate de baryum ou de strontium d’une solution équimolaire 0,10 M d’ions de baryum et de strontium sans précipiter l’autre ?

6. L’hydroxyde de fer(II) n’est que faiblement soluble dans l’eau à 25 °C ; son K_sp est égal à 7,9 × 10^-16. Calculer la solubilité (g⋅mol^-1) d’hydroxyde de fer(II) dans une solution de pH 6,0.

Réponses

1. 1.08 x 10¹³
2. 0.003 M
3. A et B
4. E
5. 3.6 x 10^-4
6. 7.9 M