5.4 – Acides polyprotiques

Nous pouvons classer les acides selon le nombre de protons par molécule qu’ils peuvent abandonner dans une réaction. Les acides tels que HCl, HNO3 et HCN qui contiennent un atome d’hydrogène ionisable dans chaque molécule sont appelés acides monoprotiques. Leurs réactions avec l’eau sont : 

HCl (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + Cl^– (aq)

HNO₃ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₃^– (aq)

HCN (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CN^– (aq)

Note : le K_a de HCN est de 6,2 x 10^-10. Cela signifie que l’acide ne s’ionise pas complètement dans l’eau et nécessite la flèche d’équilibre. 

Bien qu’il contienne quatre atomes d’hydrogène, l’acide acétique, CH3CO2H, est également monoprotique car seul l’atome d’hydrogène du groupe fonctionnel acide carboxylique (COOH) réagit avec les bases :  

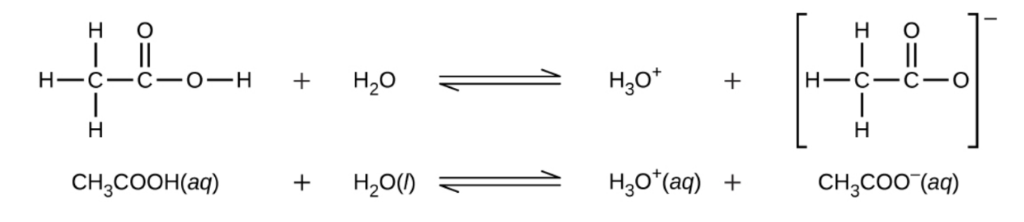
De même, les bases monoprotiques sont des bases qui acceptent un seul proton. 

Acides diprotiques 

Les acides diprotiques contiennent deux atomes d’hydrogène ionisables par molécule ; l’ionisation de ces acides se fait en deux étapes. La première ionisation a toujours lieu dans une plus large mesure que la seconde. Par exemple, l’acide sulfurique, un acide fort, s’ionise comme suit : 

Première ionisation : 

H₂SO₄ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HSO₄^– (aq)

Pour cette réaction, Ka₁ > 102, indiquant une ionisation complète à ~100% du premier proton. 

Deuxième ionisation : 

HSO₄^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + SO₄^2- (aq)

Pour cette réaction, Ka₂ = 1,0×10^-2, ce qui indique que la seconde ionisation n’est que partielle. 

Ce processus d’ionisation par étapes se produit pour tous les acides polyprotiques. Lorsque nous faisons une solution d’un acide diprotique faible, nous obtenons une solution qui contient un mélange d’acides. L’acide carbonique, _H2CO3, est un exemple d’acide diprotique faible. La première ionisation de l’acide carbonique produit des ions hydroniums et des ions bicarbonate en petites quantités. 

Première ionisation : 

H₂CO₃ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₃^– (aq)

Deuxième ionisation : 

HCO₃^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CO₃^2- (aq)

est supérieure à 

par un factuer de 10⁴, de sorte que H₂CO₃ est le producteur dominant d’ions hydronium dans la solution. Cela signifie que très peu de HCO₃^– (formé par l’ionisation de H₂CO₃) s’ionise une deuxième fois pour donner plus d’ions hydronium (et d’ions carbonate), et les concentrations de H₃O⁺ et de HCO₃^– sont pratiquement égales dans une solution aqueuse pure de H₂CO₃.  

Confirmons-nous mathématiquement ce concept très important. Les tableaux ICE ci-dessous présentent les deux réactions d’ionisation, en commençant par une solution de H₂CO₃ à 10,0 M. Remarquez qu’avec la première réaction d’ionisation, nous générons une petite concentration de H₃O⁺ et de HCO₃^– (même en commençant avec 10,0 M de H₂CO₃ !) – ceci est à nouveau dû à la valeur relativement faible de Ka_1. Ensuite, la deuxième réaction d’ionisation, qui a une valeur K_a encore plus faible, ne provoque pratiquement aucun changement dans la concentration de HCO₃^– et de H₃O⁺ et génère une quantité négligeable de CO₃^2-. 

Si la première constante d’ionisation d’un acide diprotique faible est supérieure à la seconde d’un facteur d’au moins 20, il convient de traiter la première ionisation séparément et de calculer les concentrations qui en résultent avant de calculer les concentrations des espèces résultant de l’ionisation ultérieure. Cela peut simplifier considérablement notre travail car nous pouvons déterminer la concentration de H₃O+ et de la base conjuguée de la première ionisation, puis déterminer la concentration de la base conjuguée de la seconde ionisation dans une solution dont les concentrations sont déterminées par la première ionisation. 

Exemple 5.4.1  – Ionisation d’un acide diprotique 

Lorsque nous achetons de l’eau gazeuse, nous achetons une solution de dioxyde de carbone dans l’eau. La solution est acide car le CO₂ réagit avec l’eau pour former de l’acide carbonique, H₂CO₃. Que sont [H₃O⁺], [HCO₃^–], et [CO₃^2-] dans une solution saturée de CO₂ avec un [H₂CO₃] initial = 0,033 M ? 

H₂CO₃ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₃^– (aq)     K_a1 = 4.5 x 10^-7

HCO₃^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CO₃^2- (aq)        K_a2 = 4.7 x 10^-11

Solution 

Comme l’indiquent les constantes d’ionisation, le H₂CO₃ est un acide beaucoup plus fort que le HCO₃^–, de sorte que le H₂CO₃ est le principal producteur d’ions hydronium en solution. La solution de ce problème comporte donc deux volets : (1) En suivant les quatre étapes habituelles, nous déterminons la concentration de H₃O⁺ et de HCO₃^– produite par l’ionisation de H₂CO₃. (2) Ensuite, nous déterminons la concentration de CO₃^2- dans une solution avec la concentration de H₃O⁺ et HCO₃^– déterminée en (1). Pour résumer :

Déterminer les concentrations de H₃O⁺ et de HCO₃^–. 

H₂CO₃ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₃^– (aq)          K_a1 = 4.5 x 10^-7

Quant à l’ionisation de tout autre acide faible : 

Un tableau abrégé des changements et des concentrations montre : 

              H₂CO₃ + H₂O⇌ H₃O⁺ + HCO₃^–

La substitution des concentrations d’équilibre dans l’équilibre nous donne :

K_H2CO3=([H₃O⁺][HCO₃^–])/[H₂CO₃]=x²/(0.033-x)=4.5×10^-7

La résolution de l’équation précédente en faisant nos hypothèses standard donne

x=1.2×10^-4

Ainsi:

[H₂CO₃]=0.033M

[H₃O⁺]=[HCO₃^–]=1.2×10-4M

Déterminer la concentration de CO₃^2- dans une solution à l’équilibre avec [H₃O⁺] et [HCO₃^–], tous deux égaux à 1,2 × 10^-4 M. 

HCO₃^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CO₃^2- (aq)

K_HCO3-=([H₃O+][CO₃^2-])/[HCO₃^–]=((1.2×10^-4)[CO₃^2-])/1.2×10^-4

[CO₃^2-]=((4.7×10^-11)(1.2×10^-4))/1.2×10^-4=4.7×10^-11

Pour résumer : Dans la première partie de cet exemple, nous avons constaté que le H2CO3 d’une solution à 0,033 M s’ionise légèrement et qu’à l’équilibre [H₂CO₃] = 0,033 M ; [H₃O⁺] = 1,2 × 10^-4 ; et [HCO₃^–] = 1,2×10^-4 M. Dans la deuxième partie, nous avons déterminé que [CO₃^2-] = 4,7×10^-11 M. 

Vérifiez votre apprentissage 5.4.1  – Ionisation d’un acide diprotique 

La concentration de H₂S dans une solution aqueuse saturée à température ambiante est d’environ 0,1 M. Calculez [H₃O⁺], [HS^–], et [S^2-] dans la solution : 

H₂S (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HS^– (aq)   K_a1 = 8.9 x 10^-8

HS^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + S^2- (aq)     K_a2 = 1.0 x 10^-19

Réponse

[H₂S] = 0.1 M; [H₃O⁺] = [HS⁻] = 0.000094 M; [S²⁻] = 1 × 10⁻¹⁹ M ≈ 0 M

On note que la concentration de l’ion sulfure est la même que celle du Ka₂. Cela est dû au fait que chaque ionisation ultérieure d’un acide polyprotique se produit à un degré moindre. 

Acides triprotiques 

Un acide triprotique est un acide qui possède trois protons ionisables qui subissent une ionisation progressive : L’acide phosphorique en est un exemple typique : 

Première ionisation :  

H₃PO₄ (aq) + H₂O (l) → H₃O⁺ (aq) + H₂PO₄^– (aq)   K_a1 = 7.5 x 10^-3

Deuxième ionisation : 

H₂PO₄^– (aq) + H₂O (l) → H₃O⁺ (aq) + HPO₄^2- (aq)   K_a2 = 6.2 x 10^-5

Troisième ionisation :  

HPO₄^2– (aq) + H₂O (l) → H₃O⁺ (aq) + PO₄^3- (aq)       K_a3 = 4.2 x 10^-13

Comme pour les acides diprotiques, les différences dans les constantes d’ionisation de ces réactions nous indiquent qu’à chaque étape successive, le degré d’ionisation est significativement plus faible. C’est une caractéristique générale des acides polyprotiques et les constantes d’ionisation successives diffèrent souvent d’un facteur d’environ 10⁵ à 10⁶. 

Cet ensemble de trois réactions d’ionisation peut sembler rendre compliqué le calcul des concentrations d’équilibre dans une solution de H3PO4. Cependant, comme les constantes d’ionisation successives diffèrent d’un facteur de 10⁵ à 10⁶, les calculs peuvent être décomposés en une série de parties similaires à celles des acides diprotiques. 

Bases polyprotiques 

Les bases polyprotiques peuvent accepter plus d’un ion hydrogène en solution. L’ion carbonate est un exemple de base diprotique, puisqu’il peut accepter jusqu’à deux protons. Les solutions de carbonates de métaux alcalins sont assez alcalines, en raison des réactions : 

Première protonation : 

H₂O (l) + CO₃^2- (aq) ⇌ HCO₃^– (aq) + OH^– (aq)    K_b1 = K_W/K_a2 = 2.1 × 10^-4

Deuxième protonation : 

H₂O (l) + HCO₃^– (aq) ⇌ H₂CO₃ (aq) + OH^– (aq)   K_b2 = K_W/K_a1 = 2.2 × 10^-8

Exemple 5.4.2 – Conversion entre Ka et Kb – Bases des acides polyprotiques 

Étant donné la réaction d’équilibre chimique suivante, laquelle des expressions suivantes décrit correctement sa constante d’équilibre, K : 

PO43- + H2O ⇌ OH- + HPO4-

(a) 1/Ka₂

(b) Kw/Ka₃

(c) 1/Ka₃

(d) Kw/Ka₂

Solution 

Remarquez comment dans cette réaction, la principale espèce PO₄^3- accepte un proton lorsqu’il réagit avec l’eau – cela signifie qu’il est la base de cette réaction et donc que K est plus spécifiquement K_b. Rappelons que, pour toute paire acide-base conjuguée, la relation entre K_a et K_b est : K_w = K_a × K_b. Nous pouvons déjà exclure les options (a) et (c) car elles n’incluent pas K_w dans l’expression de K. 

La réaction indiquée commence avec un ion phosphate (qui est non protoné) qui est converti en son acide monoprotique conjugué HPO₄^–. La PO₄^3- est sous sa forme la plus déprotonée (pas de protons), cette réaction est donc K_b1 – la première réaction dans laquelle la PO₄^3- capte son tout premier proton. En gardant cela à l’esprit, nous pouvons dire que cette réaction correspond à K_a3. Comme nous travaillons avec l’HPO₄^– en tant qu’acide et le PO₄^3- en tant que base conjuguée, cet équilibre peut être vu de deux façons : soit nous avons le PO₄^3- en tant que base réagissant avec l’eau pour lui faire prendre son tout premier proton et devenir l’HPO₄^3- (qui est K_b1), soit nous avons l’HPO₄^3- en tant qu’acide réagissant avec l’eau pour perdre son dernier proton et devenir le PO43- (qui est _Ka3). Nous pouvons voir que (b) et (d) ont tous deux l’expression correctement arrangée de sorte que Kw/Ka = Kb, cependant, seul (b) utilise _Ka3 pour se convertir correctement en Kb1. 

Par conséquent, la bonne réponse est (b). 

Vérifiez votre apprentissage 5.4.2 – Conversion entre Ka et Kb – Bases des acides polyprotiques 

Compte tenu des informations ci-dessous, donnez les équations chimiques équilibrées et calculez les constantes d’équilibre pour les 3 réactions de protonation successives de la base hypothétique, ^A3- (aq). 

H₃A (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + H₂A^– (aq) K_a1 = 1.5 x 10^-4

H₂A^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HA^2– (aq) K_a2 = 2.7 x 10^-9

HA^2– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^3– (aq) K_a3 = 8.8 x 10^-12

Répondez 

A^3– (aq) + H₂O (l) ⇌ OH^– (aq) + HA^2– (aq) K_b1 = K_W/K_a3 = 1.1 x 10^-3

HA^2– (aq) + H₂O (l) ⇌ OH^– (aq) + H₂A^– (aq) K_b2 = K_W/K_a2 = 3.7 x 10^-6

H₂A^– (aq) + H₂O (l) ⇌ OH^– (aq) + H₃A (aq) K_b3 = K_W/K_a1 = 6.7 x 10^-11

Questions

★ Questions

1. Laquelle des concentrations suivantes serait pratiquement égale dans un calcul des concentrations d’équilibre dans une solution de H₂CO₃, un acide diprotique, à 0,134 M [H₃O⁺], [OH⁻], [H₂CO₃], [HCO₃⁻], [CO₃²⁻]? Aucun calcul n’est nécessaire pour répondre à cette question.

2. Calculer la concentration de chaque espèce présente dans une solution de H₂S à 0,050 M. 

3. Calculer la concentration de chaque espèce présente dans une solution 0,010-M d’acide phtalique,C₆H₄(CO₂H)₂. 

★★ Questions

4. L’acide salicylique, HOC₆H₄CO₂H, et ses dérivés sont utilisés depuis longtemps comme analgésiques. L’acide salicylique est présent en petites quantités dans les feuilles, l’écorce et les racines de certains végétaux (plus particulièrement, historiquement, dans l’écorce du saule). Les extraits de ces plantes sont utilisés comme médicaments depuis des siècles. L’acide a été isolé pour la première fois en laboratoire en 1838. 

(a) Les deux groupes fonctionnels de l’acide salicylique s’ionisent dans l’eau, avec K_a = 1,0 × 10-3 pour le groupe -CO₂H et 4,2 × 10^-13 pour le groupe -OH. Quel est le pH d’une solution saturée de l’acide (solubilité = 1,8 g/L). 

(b) L’aspirine a été découverte grâce aux efforts déployés pour produire un dérivé de l’acide salicylique qui ne serait pas irritant pour la paroi de l’estomac. L’aspirine est l’acide acétylsalicylique, CH3CO2C6H4CO2H. Le groupe fonctionnel -CO₂H est toujours présent, mais son acidité est réduite, Ka = 3,0 × 10^-4. Quel est le pH d’une solution d’aspirine à la même concentration qu’une solution saturée d’acide salicylique (voir partie a). 

(c) Dans certaines conditions, l’aspirine réagit avec l’eau et forme une solution d’acide salicylique et d’acide acétique : 

CH₃CO₂C₆H₄CO₂H (aq) + H₂O (l) ⇌ HOC₆H₄CO₂H (aq) + CH₃CO₂H (aq)

(i) Lequel des acides, l’acide salicylique ou l’acide acétique, produit le plus d’ions hydronium dans une telle solution ? 

(ii) Quelles sont les concentrations de molécules et d’ions dans une solution produite par l’hydrolyse de 0,50 g d’aspirine dissoute dans suffisamment d’eau pour donner 75 ml de solution ? 

5. L’ion HTe^– est une espèce amphiprotique ; il peut agir soit comme un acide, soit comme une base. 

(a) Qu’est-ce que le K_a pour la réaction acide de la HTe^– avec l’H₂O ? 

(b) Quelle est la valeur de K_b pour la réaction dans laquelle le HTe^– fonctionne comme une base dans l’eau ? 

(c) Démontrer si la seconde ionisation de H₂Te peut ou non être négligée dans le calcul de [HTe^–] dans une solution de H₂Te à 0,10 M. 

Réponses

1. [H₃O⁺] et [HCO₃⁻] sont pratiquement égaux 

2. [HS] = 7.1 x 10⁻⁵ M, [H₃O⁺] = 7.1 x 10⁻⁵ M, [S⁻²] = 1.29 x 10⁻¹³ M, [H₂S] = 0.0499 M

[C₆H₄(CO₂)₂^2-(aq)]=3.9×10^-6 M, [OH-]=3.6×10^-12 M

4 (a) pH = 2.44, (b) pH = 2.70,

(c) (i) acide salicylique (ii) La concentration d’aspirine et d’acide acétique est de 2,1 x 10^-4 M 

5 (a) K_a2=1.5×10^-11

(b) K_b=4.3×10^-12

(c) ([Te^2-][H₃O⁺(aq)])/[HTe^–]=((x)(0.0141+x))/(0.0141-x)≈((x)(0.0141))/(0.0141)=1.5×10^-11

La résolution de x donne  1.5×10^-11 M. Par conséquent, par rapport à 0,014 M, cette valeur est négligeable (1.1×10^-7%).