5.3 – Forces des acides/bases

Nous pouvons classer les forces des acides en fonction de leur degré d’ionisation en solution aqueuse. La réaction d’un acide avec l’eau est donnée par l’expression générale : 

HA (aq) + H₂O (aq) ⇌ H₃O⁺ (aq) + A^– (aq)

L’eau est la base qui réagit avec l’acide HA, A- est la base conjuguée de l’acide HA, et l’ion hydronium est l’acide conjugué de l’eau. Un acide fort donne 100 % de H₃O⁺ et de A- lorsque l’acide s’ionise dans l’eau ; la figure 5.3.1 énumère plusieurs acides forts. Si nous commençons avec 0,1 M HCl, à l’équilibre nous obtenons 0,1 M H₃O⁺ et 0,1 M Cl^–. Selon la définition de Brønsted-Lowry, en tant qu’acide fort, le HCl est un très bon donneur de protons. Pour une réaction d’un acide fort avec l’eau, l’équation chimique générale ci-dessus s’applique, sauf que le symbole d’équilibre est généralement remplacé par une flèche à sens unique pour indiquer que la réaction est entièrement terminée : 

HA (aq) + H₂O (l) → H₃O⁺ (aq) + A^– (aq)

Un acide faible donne des quantités de H₃O⁺ et de A- qui représentent une ionisation bien inférieure à 100 %. Ainsi, en se référant à la définition de Brønsted-Lowry, on peut dire que les acides faibles sont de mauvais donneurs de protons. 

Pour une réaction d’un acide faible avec l’eau, l’équation chimique générale indiquée en premier lieu dans cette section s’applique – nous utilisons une flèche d’équilibre pour indiquer que la réaction n’est pas terminée et qu’à l’équilibre, les deux réactifs sont des produits sont présents : 

Figure 5.3.1. Certains des acides et bases forts les plus courants sont énumérés ici. 

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

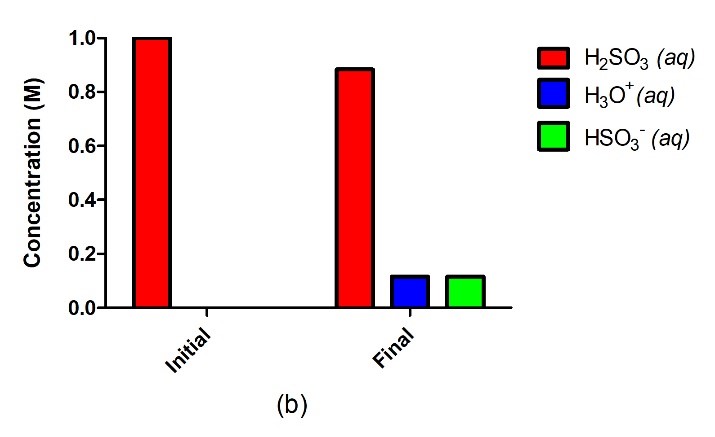
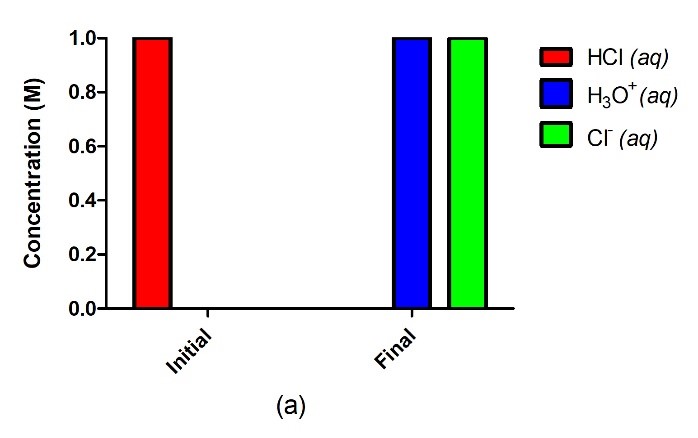
Figure 5.3.2. Un acide fort tel que le HCl dans l’eau (a) s’ionise complètement et s’achève sans qu’il ne reste de réactif, où 1,0 M de HCl donne 1,0 M de H₃O⁺ et 1,0 M de Cl^–. Un acide faible tel que H₂SO₃ (b), en revanche, ne s’ionisera que partiellement dans l’eau, ce qui nous donne un mélange équilibré de réactifs et de produits. 

Si vous vous souvenez du chapitre précédent sur les équilibres chimiques, vous remarquerez que cette notion de rapport entre les produits et les réactifs est exactement la façon dont nous exprimons les constantes d’équilibre ! Par conséquent, nous pouvons utiliser ces connaissances pour déterminer les forces relatives des acides en mesurant leurs constantes d’équilibre dans les solutions aqueuses. Dans des solutions de même concentration, les acides les plus forts s’ionisent complètement, et donnent donc des concentrations d’ions hydronium plus élevées que les acides plus faibles. Lors de l’écriture d’une équation pour l’ionisation d’un acide fort, une flèche à sens unique est utilisée afin de montrer qu’il s’agit d’une réaction complète. Alors que tout acide dont l’ionisation est inférieure à 100% est techniquement classé comme “acide faible”, pour la plupart des acides faibles, à l’équilibre, seule une très petite fraction de l’acide sera ionisée. La constante d’équilibre d’un acide est appelée constante d’ionisation de l’acide, _Ka. Pour la réaction d’un acide HA : 

HA (aq) + H₂O (l) ⇌    H₃O⁺ (aq) + A- (aq) 

nous écrivons l’équation de la constante d’ionisation comme : 

K_a = ([H₃O⁺][A^–])/[HA]

où les concentrations sont celles à l’équilibre. Rappelons du chapitre 4 que bien que l’eau soit un réactif dans la réaction, c’est un liquide, son activité est égale à 1, et donc elle n’apparaît pas dans l’expression K_a.Plus le K_a d’un acide est grand, plus la concentration de H₃O⁺ et de A^– est grande par rapport à la concentration de l’acide neutre et syndiqué, HA. Ainsi, un acide plus fort a une constante d’ionisation plus grande qu’un acide plus faible, et les constantes d’ionisation augmentent avec la force des acides. Le tableau 5.2.1, qui se trouve plus loin dans cette section, énumère les valeurs des constantes d’ionisation de quelques acides faibles courants ; un tableau plus complet des valeurs de Ka se trouve à l’annexe H. 

Pour illustrer cela, considérons les trois équilibres acides ci-dessous : les constantes d’ionisation de l’acide indiquent que l’ordre de la force de l’acide pour ces acides est : CH₃CO₂H < HNO₂ < HSO₄⁻.

CH₃CO₂H (aq) + H₂O (aq) → H₃O⁺ (aq) + CH₃CO₂^– (aq) K_a = 1.8 x 10^–5

HNO₂ (aq) + H₂O (l) → H₃O⁺ (aq) + NO₂^– (aq) K_a = 4.6 x 10^–4

HSO₄^– (aq) + H₂O (l) → H₃O⁺ (aq) + SO₄^2- (aq) K_a = 1.2 x 10^–2

Une autre mesure de la force d’un acide est son pourcentage d’ionisation. Le pourcentage d'ionisation d’un acide faible est le rapport entre la concentration de l’acide ionisé et la concentration initiale de l’acide, multiplié par 100 : 

%ionization = ([H₃O⁺]_eq/[HA]₀]×100

Comme le rapport inclut la concentration initiale, le pourcentage d’ionisation pour une solution d’un acide faible donné varie en fonction de la concentration initiale de l’acide, et diminue en fait avec l’augmentation de la concentration de l’acide…mais pourquoi ?  

Revenons sur l’équilibre de l’ionisation des acides, en utilisant à nouveau l’HA comme acide faible générique avec une valeur K_a de 1,00×10^-5 : 

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A- (aq)     K_a = 1,00 x 10^-5 

Imaginez que nous ayons 1 L d’eau et que nous ajoutions exactement 0,100 mole de cet acide faible, ce qui donne une valeur initiale de [HA]₀ = 0,100 M. En suivant la méthode du tableau ICE présentée au chapitre 4, nous constatons qu’à l’équilibre, la solution contient 0,00100 M de H₃O⁺, ce qui donne un pourcentage d’ionisation d’exactement 1,0 % (prenez un moment pour confirmer ce calcul par vous-même). Imaginez maintenant que nous augmentions la quantité d’acide initiale, en ajoutant 0,100 mole supplémentaire à la solution existante, ce qui donne un total de 0,200 mole de HA dans 1 L d’eau, donc [HA]₀ = 0,200 M. Cette deuxième addition de 0,100 mole de HA tente d’ioniser une solution qui contient déjà 0,00100 M H₃O⁺ produit à partir de la première 0,100 mole de HA ajoutée. Selon le principe de Le Chatelier, l’augmentation de la quantité d’un produit déplace l’équilibre vers les réactifs. Par conséquent, il est préférable de ne pas essayer de produire du H₃O⁺ dans une solution qui en contient déjà un peu. En d’autres termes, la présence d’un peu de H₃O⁺ provenant de la première addition de 0,100 mol HA inhibe l’ionisation de la seconde addition de 0,100 mol HA. Nous pouvons le confirmer en refaisant le calcul de la table ICE : une valeur de [HA]₀ = 0,200 M donne une concentration d’équilibre de 0,00141 M H₃O⁺ et un pourcentage d’ionisation de 0,71% (là encore, vous devriez confirmer ces valeurs vous-même). Remarquez comment la quantité totale de H₃O⁺ à l’équilibre a effectivement augmenté (parce que nous avons ajouté plus de HA), mais la fraction ionisée est devenue plus petite : c’est le principe de Le Chatelier en action ! 

C’est un concept très important, il est donc prudent de le souligner à nouveau, comme l’illustre la figure 5.3.3 ci-dessous. Cette figure montre le pourcentage d’ionisation et la concentration d’équilibre de H₃O⁺ pour l’ionisation de l’acide nitreux, HNO₂ : 

HNO2 (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO^2- (aq)        K_a = 5,6 x 10^-4

L’augmentation de la concentration initiale de HNO₂ augmentera la quantité de H₃O⁺ produite à l’équilibre. Cependant, en ajoutant de plus en plus d’acide nitreux, on inhibe davantage l’ionisation, favorisant plutôt la réaction inverse. Par conséquent, ce qui est directement affecté n’est pas la concentration finale de H₃O⁺  à l’équilibre (qui continue à augmenter) mais plutôt l’étendue réelle de l’ionisation de l’acide – quelle fraction de l’acide s’ionise réellement avec succès en solution. Donc, en conclusion, à mesure que [HNO₂]_{0 augmente,} [H₃O⁺]_eq augmente, mais le pourcentage d’ionisation de HNO₂ diminue.  

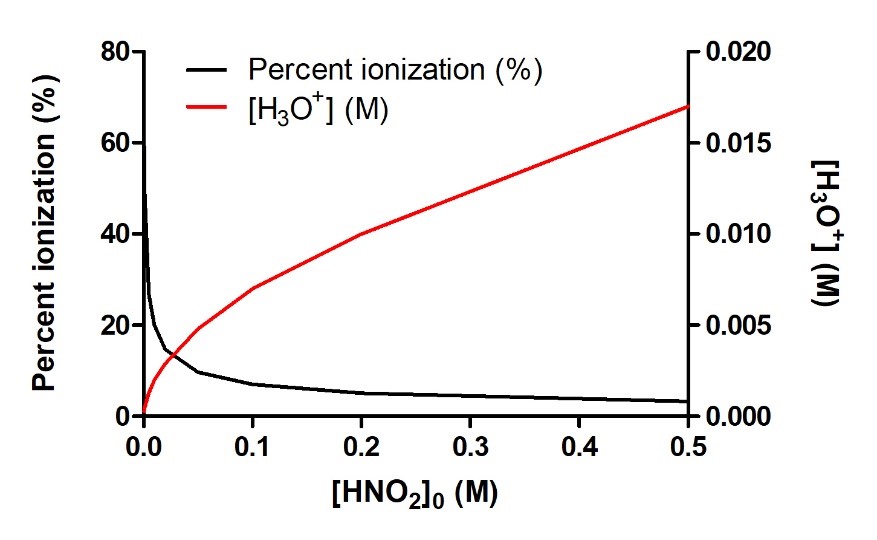
Figure 5.3.3. À mesure que la concentration de HNO₂ augmente en solution aqueuse, la concentration de H₃O⁺  produit augmente également ; cependant, la fraction de la concentration initiale qui est ionisante diminue, comme l’indique la diminution du pourcentage d’ionisation. 

Essayez-le vous-même – Pourcentage d’ionisation et [H₃O⁺]_eq par rapport à la concentration initiale d’acide 

La valeur K_a de l’acide benzoïque est d’environ 6,25 × 10^-5. L’équation d’équilibre pour l’ionisation de l’acide benzoïque est la suivante : 

C₆H₅COOH_(aq) + H₂O_(l) ⇌ C₆H₅COO^–_(aq) + H₃O⁺_(aq)

Supposons que le K_a soit constant et que vous ne commenciez qu’au début avec un réactif (c’est-à-dire l’acide benzoïque). Utilisez un logiciel de tableur (par exemple Microsoft Excel, Google Sheets) : 

Déterminez l’équivalent en [H₃O⁺] et le pourcentage d’ionisation aux concentrations initiales suivantes d’acide benzoïque : 0,005 M, 0,010 M, 0,020 M, 0,025 M, 0,050 M, 0,075 M, 0,10 M, 0,25 M, 0,5 M, 1,0 M. (Conseil : rappelez-vous que l’ionisation de l’acide est une réaction d’équilibre… utilisez la résolution de problèmes de réaction d’équilibre pour vous aider). 

En utilisant ces données, tracez un graphique de [C6H5COOH]₀ (concentration initiale d’acide benzoïque) en fonction de [H₃O⁺]_eq sur un axe des ordonnées et du pourcentage d’ionisation sur un autre axe des ordonnées. 

Remarquez-vous des tendances ? Pouvez-vous les expliquer ? 

Exemple 5.3.1 – Calcul du pourcentage d’ionisation à partir du pH 

Calculer le pourcentage d’ionisation d’une solution d’acide nitreux (un acide faible) de 0,125 M, avec un pH de 2,09. 

Solution 

Le pourcentage d’ionisation pour un acide est : 

([H₃O⁺]_eq/[HNO₂]₀)×100

L’équation chimique pour l’ionisation de l’acide nitreux est :  

HNO₂ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₂^– (aq) K_a = 5.6 x 10^–4

Puisque 10^-pH = [H₃O⁺], nous constatons que 10^-2,09 = 8,1 × 10-3 M, ce qui correspond à un pourcentage d’ionisation :

8.1×10^-30.125×100=6.5%

Rappelez-vous que le logarithme 2,09 indique une concentration d’ions hydronium avec seulement deux chiffres significatifs. 

Vérifiez votre apprentissage 5.3.2 – Calcul du pourcentage d’ionisation à partir du pH 

Calculer le pourcentage d’ionisation d’une solution d’acide acétique à 0,10 M avec un pH de 2,89. 

Réponse 

1,3 % ionisé 

Nous pouvons classer les forces des bases selon leur tendance à former des ions hydroxyde en solution aqueuse. La réaction générale d’une base de Brønsted-Lowry avec l’eau est donnée par : 

B (aq) + H₂O (l) → HB⁺ (aq) + OH^– (aq) 

L’eau est l’acide qui réagit avec la base, HB+ est l’acide conjugué de la base B, et l’ion hydroxyde est la base conjuguée de l’eau. Une base forte produit 100 % (ou presque) de OH- et HB+ lorsqu’elle réagit avec l’eau ; la figure 5.3.1. énumère plusieurs bases fortes. Sur la base de la définition de Brønsted-Lowry, nous pourrions caractériser les bases fortes comme étant de très bons accepteurs de protons (c’est-à-dire qu’elles ont une forte tendance à accepter les protons des acides). Une base faible produit une faible proportion d’ions hydroxyde et est donc un mauvais accepteur de protons. Les hydroxydes ioniques solubles tels que le NaOH sont considérés comme des bases fortes car ils s’ionisent complètement lorsqu’ils sont dissous dans l’eau. Vous pouvez voir une simulation PhET des acides et bases forts et faibles au niveau moléculaire en cliquant ici. 

Comme nous l’avons fait pour les acides, nous pouvons mesurer les forces relatives des bases en mesurant leur constante d’ionisation (Kb) dans les solutions aqueuses. Dans des solutions de même concentration, les bases les plus fortes s’ionisent davantage, et donnent donc des concentrations d’ions hydroxyde plus élevées que les bases plus faibles. Une base plus forte a une constante d’ionisation plus élevée qu’une base plus faible. Pour la réaction d’une base, B : 

B (aq) + H₂O (l) → HB⁺ (aq) + OH^– (aq) 

nous écrivons l’équation de la constante d’ionisation comme : 

K_b = ([HB⁺][OH^–])/[B]

où les concentrations sont celles à l’équilibre. Là encore, nous n’incluons pas  H₂O dans l’équation car l’eau est un liquide dont l’activité est égale à 1. Comme pour les valeurs de K_a, il existe une large gamme de valeurs de Kb connues, comme le montrent les trois exemples ci-dessous :  

NO₂^– (aq) + H₂O (l) ⇌ HNO₂ (aq) + HO^– (aq) K_b = 2.22 x 10^–11

CH₃CO₂^– (aq) + H₂O (l) ⇌ CH₃CO₂H (aq) + OH^– (aq) K_b = 5.6 x 10^–10

NH₃ (aq) + H₂O (l) ⇌ NH₄⁺ (aq) + OH^– (aq) K_b = 1.8 x 10^-5

Le tableau 5.2.1, qui se trouve plus loin dans cette section, énumère les valeurs des constantes d’ionisation de quelques bases faibles communes ; un tableau plus complet des valeurs de K_b se trouve à l’annexe I. 

Comme pour les acides, le pourcentage d’ionisation peut être mesuré pour les solutions basiques, mais, comme expliqué ci-dessus, cette valeur varie en fonction de la constante d’ionisation de la base et de la concentration initiale de la solution. 

Constantes d’équilibre et couples conjugués 

Examinez les réactions d’ionisation pour une paire acide-base conjuguée, HA et A^– : 

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

A^– (aq) + H₂O (l) ⇌ OH^– (aq) + HA (aq)

L’addition de ces deux équations chimiques donne l’équation de l’autoionisation de l’eau : 

HA (aq) + H₂O (l) + A^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq) + OH^– (aq) + HA (aq)

HA (aq) + H₂O (l) + A^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq) + OH^– (aq) + HA (aq)

 Simplifie à :  2 H₂O (l) ⇌ H₃O⁺ (aq) + OH^– (aq)

Comme nous l’avons vu au chapitre 4, l’expression K de toute équation chimique obtenue par l’addition de deux ou plusieurs autres équations est égale au produit mathématique des différentes expressions K. En multipliant les constantes d’équilibre ensemble et en annulant les termes communs, nous voyons cela :

K_a×K_b = ([H₃O⁺][A^–]/[HA])×([HA][OH^–]/[A^–]) =[H₃O⁺][OH^–] = K_w

Par exemple, la constante d’ionisation de l’acide acétique (CH₃COOH) est de 1,8 × 10^-5, et la constante d’ionisation de sa base conjuguée, l’ion acétate (CH3COO-), est de 5,6 × 10^-10. Le produit de ces deux constantes est en effet égal à K_W : 

K_a×K_b= (1.8×10^-5)×(5.6×10^-10) = 1.0×10^-14  =K_w

La mesure dans laquelle un acide, HA, donne des protons aux molécules d’eau dépend de la force de la base conjuguée, A^–, de l’acide. Si A^– est une base forte (un bon accepteur de protons), tous les protons qui sont donnés aux molécules d’eau pour former des ions hydroniums sont facilement recapturés par A^– pour régénérer l’HA. Il y a donc relativement peu de A^– et de H₃O⁺ en solution, et l’acide, HA, est faible. Si A^– est une base faible (mauvais accepteur de protons), il reste sous sa forme déprotonée, et la solution contient principalement A^– et H₃O⁺, et par conséquent l’acide est fort. Nous en tirons donc la conclusion importante suivante :

Les acides forts forment des bases conjuguées très faibles, et les bases fortes forment des acides conjugués très faibles 

Ceci est illustré dans la figure 5.3.4 : à mesure que l’intensité relative de l’acide augmente de droite à gauche dans la barre supérieure, vous pouvez voir que l’intensité des bases conjuguées correspondantes diminue de droite à gauche dans la barre inférieure. 

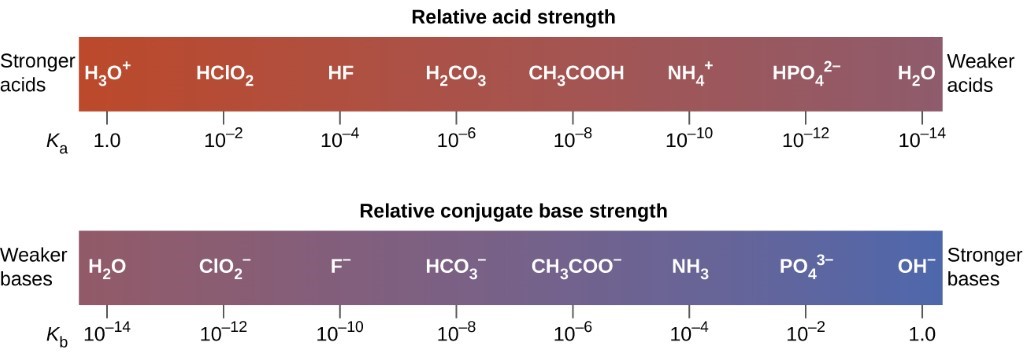
Figure 5.3.4. Ce diagramme montre les forces relatives des paires acide-base conjuguées, telles qu’indiquées par leurs constantes d’ionisation en solution aqueuse. 

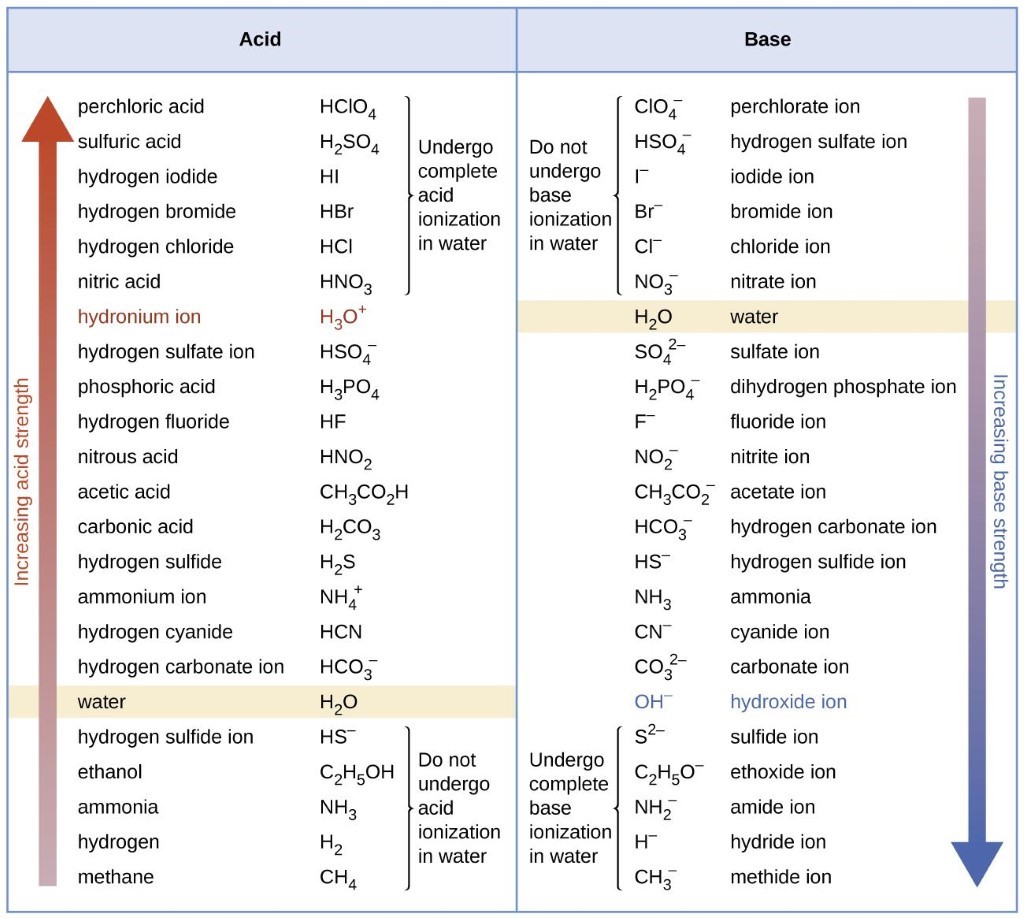
Figure 5.3.5. Le graphique montre les forces relatives des paires acide-base conjuguées. 

La figure 5.3.5 illustre également ce concept : les six premiers acides énumérés à gauche sont les acides forts les plus courants. Ces acides sont complètement ionisés en solution aqueuse. Les bases conjuguées de ces acides sont des bases plus faibles que l’eau. Lorsqu’un de ces acides se dissout dans l’eau, ses protons sont complètement transférés à l’eau, la base la plus forte. 

Les acides qui se trouvent entre l’ion hydronium et l’eau dans la figure 5.3.5 forment des bases conjuguées qui peuvent entrer en compétition avec l’eau pour la possession d’un proton. Les ions hydroniums et les molécules d’acides unionisés sont tous deux présents en équilibre dans une solution de l’un de ces acides. Les composés qui sont des acides plus faibles que l’eau (ceux que l’on trouve sous l’eau dans la colonne des acides) dans la figure 5.3.5 ne présentent aucun comportement acide observable lorsqu’ils sont dissous dans l’eau. Leurs bases conjuguées sont plus fortes que l’ion hydroxyde ; si une base conjuguée quelconque était formée, elle réagirait avec l’eau pour former l’ion hydroxyde. 

La mesure dans laquelle une base forme des ions hydroxyde en solution aqueuse dépend de la force de la base par rapport à celle de l’ion hydroxyde, comme le montre la dernière colonne de la figure 5.3.5. Une base forte, telle que celle qui se trouve sous l’ion hydroxyde, accepte les protons de l’eau pour donner 100 % de l’acide conjugué et de l’ion hydroxyde. Les bases situées entre l’eau et l’ion hydroxyde acceptent les protons de l’eau, mais il en résulte un mélange de l’ion hydroxyde et de la base. Les bases plus faibles que l’eau (celles qui se trouvent au-dessus de l’eau dans la colonne des bases) ne présentent aucun comportement basique observable en solution aqueuse. 

Exemple 5.3.2 – Le produit Ka × Kb = Kw 

En utilisant une valeur Kb de 1,8 × 10^-11 pour l’ion nitrite, NO2-^, calculer le Ka de son acide conjugué. 

Solution 

L’acide conjugué de NO₂^– est HNO₂ ; K_a pour HNO₂ peut être calculé en utilisant la relation 

K_a×K_b = 1.0×10^-14 =K_w

Résoudre pour K_a, on obtient : 

K_a= K_wxK_b = 1.0×10^-141.8×10^-11 =5.6×10^-4

Cette réponse correspond au K_a pour le HNO₂ trouvé dans le tableau 5.2.1 et dans l’annexe H. 

Vérifiez votre apprentissage 5.3.2 – Le produit Ka × Kb = Kw 

Nous pouvons déterminer les forces acides relatives du NH4+ et du HCN en comparant leurs constantes d’ionisation. La constante d’ionisation du HCN est donnée à l’annexe H sous la forme 6,2 × 10^-10. La constante d’ionisation de NH₄⁺ n’est pas indiquée, mais la constante d’ionisation de sa base conjuguée, NH₃, est indiquée comme étant de 1,8 × 10^-5. Déterminez la constante d’ionisation de NH₄⁺, et décidez quel est l’acide le plus fort, HCN ou NH₄⁺. 

Réponse 

Le HCN est l’acide légèrement plus fort (K_a pour NH₄⁺ = 5,6 × 10^-10). 

Rappelez-vous ce que nous avons évoqué précédemment concernant la relation entre les acides et les bases conjugués : les acides et les bases fortes donneront respectivement des bases et des acides conjugués très faibles. Nous pouvons utiliser ce fait pour prédire la direction du changement net sur une réaction d’équilibre acide-base – la direction privilégiée de la réaction sera de l’espèce la plus forte à l’espèce la plus faible d’une paire conjuguée. Cette force relative peut être évaluée soit qualitativement à l’aide d’un graphique qui montre les forces relatives des paires acide-base conjuguées (comme dans la figure 5.3.5), soit quantitativement à l’aide des valeurs Ka et Kb, sachant que des valeurs Ka et Kb plus élevées indiquent des acides et des bases plus forts, respectivement. Un exemple est présenté ci-dessous pour illustrer ce point. 

Exemple 5.3.3 – Prévision des produits et de la direction du changement net – Équilibres acido-basiques 

Pour la réaction acide-base suivante, il faut prévoir les produits et déterminer la direction de changement préférée (c’est-à-dire la réaction directe, K > 1, ou la réaction inverse, K < 1) : 

H₃PO₄ + HS^– 

Solution 

(a) H₃PO₄ se trouve beaucoup plus haut dans le graphique (figure 5.3.5) que HS^– dans la colonne des acides, ce qui signifie que c’est l’espèce qui donnera de préférence son proton. Il s’agit donc de notre acide donneur de protons et l’ion bisulfure est notre base acceptrice de protons. Cela nous donne la réaction d’équilibre suivant

H₃PO₄    +    HS^– ⇌     H₂PO₄^–     +     H₂S 

acide          base          base conj.       acide conj. 

Pour déterminer la direction de réaction préférée, nous devons comparer les forces relatives de l’acide (dans ce cas, H₃PO₄) et de l’acide conjugué (H₂S) dans cet équilibre : l’acide le plus fort est le meilleur donneur de protons, et aura donc plus de succès à donner son proton. Par conséquent, la direction d’équilibre préférée est toujours celle de l’acide le plus fort vers l’acide le plus faible. En examinant les paires acide-base conjuguées dans le graphique, on constate que H₃PO₄ est l’acide relativement plus fort par rapport à H₂S (de même, HS^– est la base relativement plus forte par rapport à H₂PO₄^–). Par conséquent, les réactifs sont les espèces les plus fortes et la réaction se déroule donc de préférence vers la droite, c’est-à-dire vers les produits (K > 1). 

Nous pouvons également vérifier notre conclusion à l’aide des valeurs Ka et Kb (annexes H et I). Examinons d’abord les valeurs Ka des réactifs pour confirmer le choix des produits : les valeurs Ka pour H3PO4 et HS- sont respectivement de 6,9 × 10^-3 et 1 × 10^-19. Parmi les deux, l’acide phosphorique a une valeur Ka plus élevée, il est donc le meilleur donneur de protons et se comportera donc comme l’acide dans cette réaction. Par conséquent, cela fait du HS- la base, l’accepteur de protons, et donc les produits prévus, H2PO4- et H2S, sont corrects. 

Ensuite, utilisons les valeurs Ka de l’acide et de l’acide conjugué pour confirmer la direction de réaction préférée prévue. En comparant ces valeurs Ka, nous constatons que H3PO4 est effectivement le meilleur donneur de protons (Ka = 6,9 × 10^-3) _{que H2S (Ka} = 8,9 × 10^-8). De plus, si nous calculons et comparons les valeurs de Kb entre les bases, HS- est plus fort (Kb = 1,1 × 10-7) que H2PO4- (Kb = 1,4 × 10^-12). Par conséquent, nous confirmons que les réactifs sont les espèces les plus fortes et que la direction du changement net est vers la droite. 

Vérifiez votre apprentissage 5.3.3 – Prévision des produits et de la direction du changement net – Équilibres acido-basiques 

Prévoir les produits et déterminer la direction de changement préférée pour la réaction acide-base suivante : 

HCO₃^– + HSO₃^– 

Réponse 

Les produits sont le SO₃^2- et le H₂CO³. La direction de la variation nette sera vers la gauche (c’est-à-dire les réactifs HCO₃^– et HSO₃^–). 

L’ionisation des acides faibles et des bases faibles 

De nombreux acides et bases sont faibles, c’est-à-dire qu’ils ne s’ionisent pas complètement en solution aqueuse. Une solution d’un acide faible dans l’eau est un mélange de l’acide unionisé, de l’ion hydronium et de la base conjuguée de l’acide, l’acide unionisé étant présent en plus grande concentration. Ainsi, un acide faible augmente la concentration en ions hydronium dans une solution aqueuse (mais pas autant que la même quantité d’un acide fort). 

L’acide acétique, CH₃CO₂H, est un acide faible. Lorsque nous ajoutons de l’acide acétique à l’eau, il s’ionise dans une faible mesure selon l’équation : 

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

donnant un mélange d’équilibre avec la majeure partie de l’acide présent sous la forme non-ionisée (moléculaire). Cet équilibre, comme les autres équilibres, est dynamique ; les molécules d’acide acétique donnent des ions hydrogène aux molécules d’eau et forment des ions hydroniums et des ions acétate au même rythme que les ions hydroniums donnent des ions hydrogène aux ions acétate pour reformer les molécules d’acide acétique et les molécules d’eau. On peut dire en mesurant le pH d’une solution aqueuse de concentration connue que seule une fraction de l’acide faible est ionisée à tout moment (figure 5.3.4.). L’acide faible restant est présent sous la forme ionisée. 

Pour l’acide acétique, à l’équilibre :

K_a= ([H₃O(aq)+][CH₃CO₂(aq)^–]/[CH₃CO₂H(aq)]) = 1.8×10^-5

Figure 5.3.4. Le papier pH indique qu’une solution 0,1 M de HCl (bécher à gauche) a un pH de 1. L’acide est entièrement ionisé et [H₃O⁺] = 0,1 M. Une solution 0,1 M de CH₃CO₂H (bécher à droite) a un pH de 3 ([H₃O⁺= 0,001 M) parce que l’acide faible CH₃CO₂H n’est que partiellement ionisé. Dans cette solution, [H₃O⁺] < [CH₃CO₂H]_. (crédit : modification du travail par Sahar Atwa) 

Tableau 5.2.1 Constantes d’ionisation et pH (0,1 M) de certains acides faibles 

Le tableau ci-dessus donne les constantes d’ionisation pour plusieurs acides faibles, y compris le pH pour une solution de 0,1 M de chaque acide ; des constantes d’ionisation supplémentaires sont présentées à l’annexe H. 

En examinant le pH de chaque solution à 0,1 M de chaque acide faible, il est important d’apprécier l’ampleur considérable de la différence d’acidité entre les divers acides faibles. Par exemple, les valeurs de K_a pour HCO₂H et CH₃COOH ne semblent pas très différentes, et leurs valeurs de pH ne diffèrent que de 0,5 unité. Cependant, nous devons comprendre que le K_a du HCO₂H est en fait 10 fois plus grand que celui du CH₃COOH, et qu’en termes de différence d’acidité (différence en [H₃O⁺]), il est environ 3 fois plus acide. Considérons maintenant la différence entre HCO₂H et HBrO – une différence de pH d’environ 2,4 unités. Cela ne semble pas beaucoup, mais si nous traduisons cela en termes d’acidité… une solution de 0,1 M de HCO₂H est environ 250 fois plus acide que 0,1 M de HBrO ! Par conséquent, lorsque vous rencontrez ces différences apparemment minimes de pH, gardez à l’esprit qu’il s’agit d’une échelle logarithmique et que leur acidité diffère en fait de manière significative. 

À l’équilibre, une solution d’une base faible dans l’eau est un mélange de la base non-ionisée, de l’acide conjugué de la base faible et de l’ion hydroxyde, la base non-ionisée étant présente en plus grande concentration. Ainsi, une base faible augmente la concentration d’ions hydroxyde dans une solution aqueuse (mais pas autant que la même quantité d’une base forte). 

Par exemple, une solution de la base faible triméthylamine, (CH3)₃N_, dans l’eau réagit selon l’équation : 

(CH₃)₃N (aq) + H₂O (l) ⇌ (CH₃)₃NH⁺ (aq) + OH^– (aq)

donnant un mélange d’équilibre avec la majeure partie de la base présente sous forme d’amine syndiquée. Cet équilibre est analogue à celui décrit pour les acides faibles. 

On peut confirmer, en mesurant le pH d’une solution aqueuse d’une base faible de concentration connue, que seule une fraction de la base réagit avec l’eau (figure 5.3.5.). La base faible restante est présente sous la forme n’ayant pas réagi. La constante d’équilibre pour l’ionisation d’une base faible, K_b, est appelée constante d’ionisation de la base faible, et est égale au quotient de réaction lorsque la réaction est à l’équilibre. Pour la triméthylamine, à l’équilibre: 

Kb=([(CH₃)₃NH(aq)⁺][OH^–(aq)]/[(CH₃)₃N(aq)])

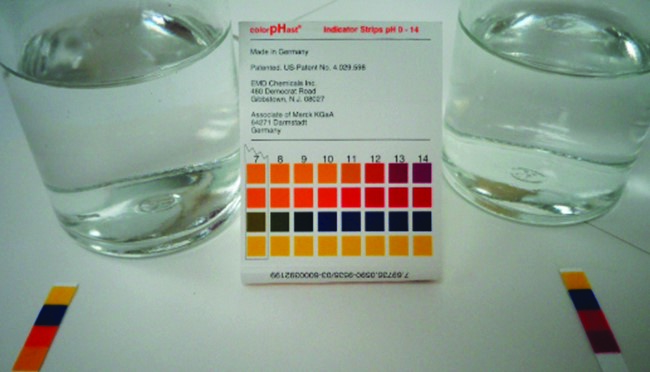
Figure 5.3.5. Le papier pH indique qu’une solution de 0,1 M de NH₃ (à gauche) est faiblement basique. La solution a un pOH de 3 ([OH_–] = 0,001 M) parce que le NH₃ faiblement basique ne réagit que partiellement avec l’eau. Une solution 0,1 M de NaOH (à droite) a un pOH de 1 parce que le NaOH est une base forte. (Crédit : modification du travail par Sahar Atwa) 

Les constantes d’ionisation de plusieurs bases faibles sont données dans le tableau ci-dessous et dans l’annexe I. 

Exemple 5.3.4  – Détermination du Ka à partir de concentrations à l’équilibre 

L’acide acétique est le principal ingrédient du vinaigre (figure 5.3.6.), ce qui lui donne un goût aigre. À l’équilibre, une solution contient [CH3CO2H] = 0,0787 M et [H₃O+] = [CH₃CO₂^–] = 0,00118 M. Quelle est la valeur de K_a pour l’acide acétique ? 

Figure 5.3.6. Le vinaigre est une solution d’acide acétique, un acide faible. (crédit : modification du travail par “HomeSpot HQ”/Flickr) 

Solution 

On nous demande de calculer une constante d’équilibre à partir des concentrations d’équilibre. À l’équilibre, la valeur de la constante d’équilibre est égale au quotient de la réaction pour la réaction : 

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

Ka= ([H₃O(aq)+][CH₃CO₂(aq)-]/[CH₃CO₂H(aq)]) = ((0.00118)(0.00118))/0.0787 =1.77×10^-5

Vérifiez votre apprentissage 5.3.4 – Détermination du Ka à partir de concentrations à l’équilibre 

Quelle est la constante d’équilibre pour l’ionisation de l’ion HSO₄^–, l’acide faible utilisé dans certains nettoyants ménagers : 

HSO₄^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + SO₄^2- (aq)

Dans un mélange de NaHSO₄ et de Na₂SO₄ à l’équilibre, [H₃O⁺] = 0,027 M ; [HSO₄^–] = 0,29 M ; et [SO₄^2-] = 0,13 M. 

Réponse 

K_a pour HSO₄⁻ = 1.2 × 10⁻²

Exemple 5.3.5 – Détermination du K_b à partir des concentrations d’équilibre 

La caféine, C₈H₁₀N₄O₂ est une base faible. Quelle est la valeur de Kb pour la caféine si une solution à l’équilibre a [C₈H₁₀N₄O₂] = 0,050 M, [C₈H₁₀N₄O₂H⁺] = 5,0 × 10-3 M, et [OH^–] = 2,5 × 10-3 M ? 

Solution 

À l’équilibre, la valeur de la constante d’équilibre est égale au quotient de réaction de la réaction : 

C₈H₁₀N₄O₂ (aq) + H₂O (l) ⇌ C₈H₁₀N₄O₂⁺ (aq) + OH^– (aq)

K_b= ([C₈H₁₀N₄O₂H(aq)+][OH(aq)-]/[C₈H₁₀N₄O₂(aq)]) = ((5.0×10^-3)(2.5×10^-3))/0.050 = 2.5×10^-4

Vérifiez votre apprentissage 5.3.5 – Détermination du K_b à partir des concentrations d’équilibre 

Quelle est la constante d’équilibre pour l’ionisation de l’ion HPO₄^2-, une base faible : 

HPO₄^2– (aq) + H₂O (l) ⇌ H₂PO₄^– (aq) + OH^– (aq)

Dans une solution contenant un mélange de NaH₂PO₄ et de Na₂HPO₄ à l’équilibre, [OH^–] = 1,3 × 10^-6 M ; [H₂PO₄^–]=0,042 M ; et [HPO₄^2-]=0,341 M. 

Réponse 

K_b pour HPO₄^2- = 1,6 × 10^-7 

Exemple 5.3.6 – Détermination de K_a ou K_b à partir du pH 

Le pH d’une solution 0,0516 M d’acide nitreux, HNO₂, est de 2,34. Quel est son K_a ? 

HNO₂ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₂^– (aq)

Solution 

Nous déterminons une constante d’équilibre à partir des concentrations initiales de HNO2, H3O+ et NO2- ainsi qu’une des concentrations finales, la concentration d’ion hydronium à l’équilibre. (N’oubliez pas que le pH est simplement une autre façon d’exprimer la concentration d’ions hydronium). Remarquez comment ce type de problème relève de l’un des deux types de problèmes d’équilibre chimique couverts dans l’unité précédente (4.3 – Résoudre les problèmes d’équilibre) – nous calculons une constante d’équilibre étant donné que nous connaissons/déterminons la concentration des réactifs et des produits à l’équilibre. 

Nous pouvons résoudre ce problème avec les étapes suivantes dans lesquelles x est un changement de concentration d’une espèce dans la réaction : 

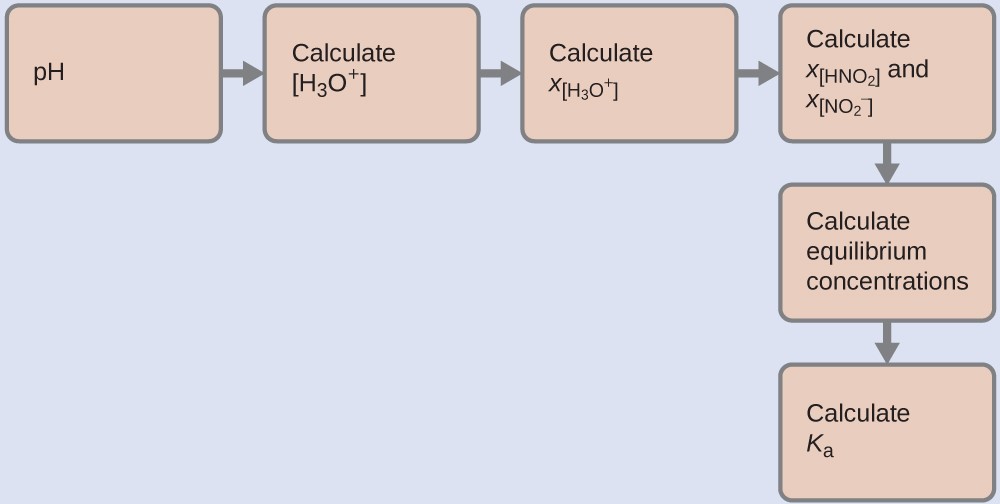
Pour obtenir les différentes valeurs dans le tableau ICE (Initial, Changement, Équilibre), nous calculons d’abord [H₃O⁺], la concentration d’équilibre de H₃O⁺, à partir du pH :

[H₃O⁺]=10^-2.34=0.0046M

Le changement de concentration de H₃O⁺, X_[H3O+], est la différence entre la concentration d’équilibre de H₃O⁺, que nous avons déterminée à partir du pH, et la concentration initiale, [H₃O⁺]_i. La concentration initiale de H₃O⁺ est sa concentration dans l’eau pure, 1 x 10-7 M, qui est tellement inférieure à la concentration finale que nous pouvons l’approcher de zéro (~0) afin de simplifier nos calculs. 

La variation de concentration de NO2- est égale à la variation de concentration de [H₃O⁺] : la stœchiométrie de la réaction indique que pour chaque mole de H₃O⁺ qui se forme, il se forme 1 mole de NO2-. La concentration d’équilibre de HNO2 est égale à sa concentration initiale plus la variation de sa concentration. 

Nous pouvons maintenant remplir le tableau ICE avec les concentrations à l’équilibre, comme indiqué ici : 

HNO₂           +    H2O             ⇌         H₃O⁺     +       NO₂^–

Enfin, nous calculons la valeur de la constante d’équilibre en utilisant les données du tableau :

K_a=([H₃O⁺][NO₂(aq)^–])/[HNO₂(aq)] = ((0.0046)(0.0046)/(0.0470) = 4.5×10^-4

Vérifiez votre apprentissage 5.3.6 – Détermination de K_a ou K_b à partir du pH 

Le pH d’une solution d’ammoniaque domestique, une solution de NH₃ à 0,950 M, est de 11,612. Quel est le K_b pour le NH₃. 

Réponse  

K_b = 1,8 × 10^-5 

Exemple 5.3.7 – Concentrations d’équilibre dans une solution d’un acide faible 

L’acide formique, HCO₂H, est l’irritant qui provoque la réaction du corps aux piqûres de fourmis (figure 5.3.7). 

Figure 5.3.7. La douleur de la piqûre d’une fourmi est causée par l’acide formique. (crédit : John Tann) 

Quelle est la concentration de l’ion hydronium et le pH dans une solution d’acide formique à 0,534 M ? 

HCO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₂^– (aq)K_a = 1.8 x 10^-4

Solution

Déterminer les concentrations x et d’équilibre. L’expression d’équilibre est :

HCO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₂^– (aq)

Le tableau indique les concentrations initiales (concentrations avant que l’acide ne s’ionise), les changements de concentration, et les concentrations d’équilibre suivent (les données dans le problème apparaissent en couleur) : 

HCO₂H + H₂O⇌ H₃O⁺ + NO₂^–

Résoudre x et les concentrations d’équilibre. A l’équilibre :

K_a=1.8×10^-4=([H₃O⁺(aq)][HCO₂^–(aq)])/[HCO₂H(aq)]

=x²/(0.534-x)=1.8×10^-4

Résolvez maintenant x. Comme la concentration initiale d’acide est raisonnablement importante et que K_a est très faible, nous faisons l’hypothèse que x << 0,534, ce qui nous permet de simplifier le terme du dénominateur comme (0,534 – x) = 0,534. Ce qui donne :

K_a=1.8×10^-4=x²/0.534

Résolvez x comme suit :

x²=0.534×(1.8×10^-4)=9.6×10^-5

x=9.6×10^-5

=9.8×10-3

Pour vérifier l’hypothèse selon laquelle x est petit par rapport à 0,534, nous calculons :

(x/0.534)x100%=1.8%

x est inférieur à 5 % de la concentration initiale et l’hypothèse est donc valable. 

Nous trouvons la concentration d’équilibre de l’ion hydronium dans cette solution d’acide formique par rapport à sa concentration initiale et la variation de cette concentration comme indiqué à la dernière ligne du tableau :

[H3O+]=∼0+x=0+9.8×10^-3M

=9.8×10^-3M

Le pH de la solution est ainsi :

pH=-log(9.8×10^-3)=2.01

Vérifiez votre apprentissage 5.3.7 – Concentrations d’équilibre dans une solution d’un acide faible 

Seule une petite fraction d’un acide faible s’ionise en solution aqueuse. Quel est le pourcentage d’ionisation de l’acide acétique dans une solution d’acide acétique 0,100 M, CH₃CO₂H ? 

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)K_a = 1,8 x 10^-5

(Conseil : déterminez [CH₃CO₂^–] à l’équilibre.) Rappelez-vous que le pourcentage d’ionisation est la fraction d’acide acétique qui est ionisée × 100, ou :

([CH₃CO₂^–(aq)]_eq/[CH₃CO₂H(aq)]_initial)×100%

Réponse 

Pourcentage d’ionisation = 1,3 

L’exemple suivant montre que la concentration des produits obtenus par l’ionisation d’une base faible peut être déterminée par la même série d’étapes que celle utilisée avec un acide faible. 

Exemple 5.3.8 – Concentrations d’équilibre dans une solution d’une base faible 

Trouvez la concentration de l’ion hydroxyde dans une solution de 0,25 M de triméthylamine, une base faible : 

(CH₃)₃N (aq) + H₂O (l) ⇌ (CH₃)₃NH⁺ (aq) + OH^– (aq)K_b = 6.3 x 10^-5

Solution 

Ce problème exige que nous calculions une concentration d’équilibre en déterminant les changements de concentration lorsque l’ionisation d’une base atteint l’équilibre. La solution est abordée de la même manière que pour l’ionisation de l’acide formique dans l’exemple précédent. Les réactifs et les produits seront différents et les nombres seront différents, mais la logique sera la même : 

Déterminer les concentrations x et d’équilibre. Le tableau montre les changements et les concentrations : 

(CH₃)₃N + H₂O⇌ (CH₃)₃NH⁺ + OH^–

Résoudre x et les concentrations d’équilibre. A l’équilibre :

K_b=([(CH₃)₃NH(aq)][OH^–(aq)]/[(CH₃)₃N(aq)])=x²/(0.25-x)=6.3×10^-5

Si nous supposons que x est petit par rapport à 0,25, alors nous pouvons remplacer (0,25 – x) dans l’équation précédente par 0,25. La résolution de l’équation simplifiée donne :

x=4.0×10^-3

Ce changement est inférieur à 5 % de la concentration initiale (0,25 M), l’hypothèse est donc justifiée. 

Rappelons que, pour ce calcul, x est égal à la concentration d’équilibre de l’ion hydroxyde dans la solution (voir le tableau précédent) :

[OH-]=∼0+x=x=4.0×10^-3 M

=4.0×10^-3

Calculez ensuite le pOH comme suit :

pH+pOH=pK_w=14.00

En utilisant la relation introduite dans la section précédente de ce chapitre :

pH+pOH=pK_w=14.00

Cela nous permet de déterminer le pH :

pH=14.00-pOH=14.00-2.40=11.60

Vérifiez le travail. Une vérification de notre arithmétique montre que K_b = 6,3 × 10^-5. 

Vérifiez votre apprentissage 5.3.8 – Concentrations d’équilibre dans une solution d’une base faible 

(a) Montrez que le calcul de l’étape 2 de cet exemple donne un x de 4,0 × 10^-3 et que le calcul de l’étape 3 montre Kb = 6,3 ×10^-5. 

(b) Trouver la concentration de l’ion hydroxyde dans une solution d’ammoniac 0,0325 M, une base faible avec un Kb de 1,76 × 10^-5. Calculez le pourcentage d’ionisation de l’ammoniac, la fraction ionisée × 100 %, ou :

([NH₄⁺]_eq/[NH₃]_i)×100%

Réponse 

7.56 × 10⁻⁴ M, 2.33% 

Certains acides faibles et certaines bases faibles s’ionisent à un tel point que l’hypothèse simplificatrice selon laquelle x est petit par rapport à la concentration initiale de l’acide ou de la base est inappropriée. En résolvant les concentrations d’équilibre dans de tels cas, nous verrons que nous ne pouvons pas négliger le changement de la concentration initiale de l’acide ou de la base, et que nous devons résoudre les équations d’équilibre en utilisant l’équation quadratique. 

Exemple 5.3.9 – Concentrations d’équilibre dans une solution d’un acide faible 

Le bisulfate de sodium, NaHSO₄, est utilisé dans certains nettoyants ménagers car il contient l’ion HSO₄^–, un acide faible. Quel est le pH d’une solution de HSO₄^– à 0,50 M ? 

HSO₄^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + SO₄^2- (aq)K_a = 1.2 x 10^-2

Solution 

Une question qui pourrait se poser est de savoir pourquoi nous n’envisageons pas le cas du HSO₄^– agissant comme accepteur de protons puisqu’il s’agit d’une espèce amphiprotique. Il y a deux raisons à cela : 1) le HSO₄^– est relativement beaucoup plus acide que l’eau (figure 5.3.5), donc dans cette réaction acide-base, il sera plus enclin à être le donneur de protons, et 2) si le HSO₄^– était l’accepteur de protons (et H₂O le donneur de protons), nous obtiendrions H₂SO₄ et OH^–. Il s’agit de produits acides et basiques très forts, de sorte qu’en fin de compte, la réaction se poursuivrait jusqu’au bout à gauche ; en d’autres termes, la réaction en avant ne se poursuivrait essentiellement pas du tout, c’est pourquoi nous pouvons écarter cette possibilité. 

Nous devons déterminer la concentration d’équilibre de l’ion hydronium qui résulte de l’ionisation du HSO₄^– afin de pouvoir utiliser [H₃O⁺] pour déterminer le pH. Comme dans les exemples précédents, nous pouvons aborder la solution par les étapes suivantes : 

Déterminer les concentrations x et d’équilibre. Ce tableau montre les changements et les concentrations : 

HSO₄^–           +       H₂O⇌ H₃O⁺ +    SO₄^2-

Résoudre le x et les concentrations. Lorsque nous commencerons à résoudre le problème de x, nous nous apercevrons que c’est plus compliqué que dans les exemples précédents. En discutant de ces complications, nous ne devons pas perdre de vue le fait que l’objectif de cette étape est toujours de déterminer la valeur de x. 

A l’équilibre :

Ka=1.2×10^-2=([H₃O⁺][SO₄^2-])/[HSO₄^–]=x²/(0.50-x)

Si l’on suppose que x est petit et que l’on obtient approximativement (0,50 – x) comme 0,50, on trouve :

x=7.7×10^-2

Lorsque nous vérifions l’hypothèse, nous calculons :

x_eq/[HSO₄^–]_i

x_eq/0.50=7.7×10^-2/0.50=0.15(15%)

La valeur de x n’est pas inférieure à 5% de 0,50, l’hypothèse n’est donc pas valable. Nous avons besoin de la formule quadratique pour trouver x. 

L’équation: 

K_a=1.2×10^-2=x²/(0.50-x)

Donne

6.0×10^-3-1.2×10^-2x=x²⁺

Ou

x²⁺+1.2×10^-2x-6.0×10^-3=0

Cette équation peut être résolue à l’aide de la formule quadratique. Pour une équation de la forme

ax²++bx+c=0

x est donné par l’équation :

x=(-b±sqrt(b²+-4ac))/2a

Dans ce problème, a = 1, b = 1,2 × 10^-3, et c = -6,0 × 10^-3. 

La résolution de x donne une racine négative et une racine positive. Comme la racine négative ne peut pas être correcte (une concentration ne peut pas être négative), nous continuerons notre solution en utilisant la racine positive :

x=7.2×10^-2

Déterminez maintenant la concentration en ions hydronium et le pH :

[H₃O⁺]=∼0+x=0+7.2×10^-2 M

=7.2×10^-2 M

Le pH de cette solution est :

pH=-log[H₃O⁺]=-log(7.2×10^-2)=1.14

Vérifiez votre apprentissage 5.3.9 – Concentrations d’équilibre dans une solution d’un acide faible 

(a) Montrer que la formule quadratique donne x = 7,2 × 10^-2. 

(b) Calculer le pH d’une solution de caféine, une base faible, à 0,010 M 

C₈H₁₀N₄O₂ (aq) + H₂O (l) ⇌ C₈H₁₀N₄O₂H⁺ (aq) + OH^– (aq)K_b = 2.5 x 10^-4

(Conseil : il sera nécessaire de convertir [OH^–] en [H₃O⁺] ou pOH en pH vers la fin du calcul). 

Réponse 

 pH = 11,16 

Les forces relatives des acides et des bases fortes 

Les acides forts, tels que le HCl, le HBr et le HI, présentent tous la même force dans l’eau. La molécule d’eau est un si bon accepteur de protons par rapport aux bases conjuguées Cl^–, Br^– et I^– que l’ionisation de ces acides forts est essentiellement complète dans les solutions aqueuses. Dans les solvants moins basiques que l’eau, nous trouvons HCl, HBr et HI qui diffèrent nettement dans leur tendance à donner un proton au solvant. Par exemple, lorsqu’ils sont dissous dans l’éthanol (une base plus faible que l’eau), l’étendue de l’ionisation augmente de l’ordre HCl < HBr < HI, et il est donc démontré que HI est le plus fort de ces acides. L’incapacité à discerner les différences de force entre les acides forts dissous dans l’eau est connue sous le nom d’effet de nivellement de l'eau. 

L’eau exerce également un effet de nivellement sur les forces des bases fortes. Par exemple, l’ion oxyde, O2-^, et l’ion amide, NH2-^, sont des bases si fortes qu’elles réagissent complètement avec l’eau : 

O^2– (aq) + H₂O (l) → OH^– (aq) + OH^– (aq)

NH₂^– (aq) + H₂O (l) → NH₃ (aq) + OH^– (aq)

Ainsi, O^2- et NH₂^– semblent avoir la même force de base dans l’eau ; ils donnent tous deux un rendement de 100% d’ion hydroxyde. Par conséquent, cela signifie que les espèces O^2- et NH₂^– n’existent pas dans les solutions aqueuses. 

Effet de la structure moléculaire sur la force acide-base 

NOTE : Ce sujet est brièvement abordé pour comprendre la force acido-basique due à la structure moléculaire. Cependant, ce sujet est beaucoup plus important et est discuté plus en détail dans le cours CHM1721 du semestre d’hiver : Chimie organique I. 

En l’absence de tout effet de nivellement, la force acide des composés binaires d’hydrogène avec des non-métaux (A) augmente à mesure que la force de liaison H-A diminue dans un groupe du tableau périodique. Pour le groupe 17, l’ordre d’augmentation de l’acidité est HF < HCl < HBr < HI. De même, pour le groupe 16, l’ordre d’augmentation de l’acidité est H₂O < H₂S < H₂Se < H₂Te. 

Sur une ligne du tableau périodique, l’acidité des composés binaires d’hydrogène augmente avec l’électronégativité croissante de l’atome non métallique car la polarité de la liaison H-A augmente (remarque : si vous n’êtes pas familier avec le concept d’électronégativité, il est abordé dans la section 9.1). Ainsi, l’ordre d’augmentation de l’acidité (pour l’élimination d’un proton) sur la deuxième ligne est CH₄ < NH₃ < H₂O < HF ; sur la troisième ligne, c’est SiH₄ < PH₃ < H₂S < HCl (voir figure 5.3.8). 

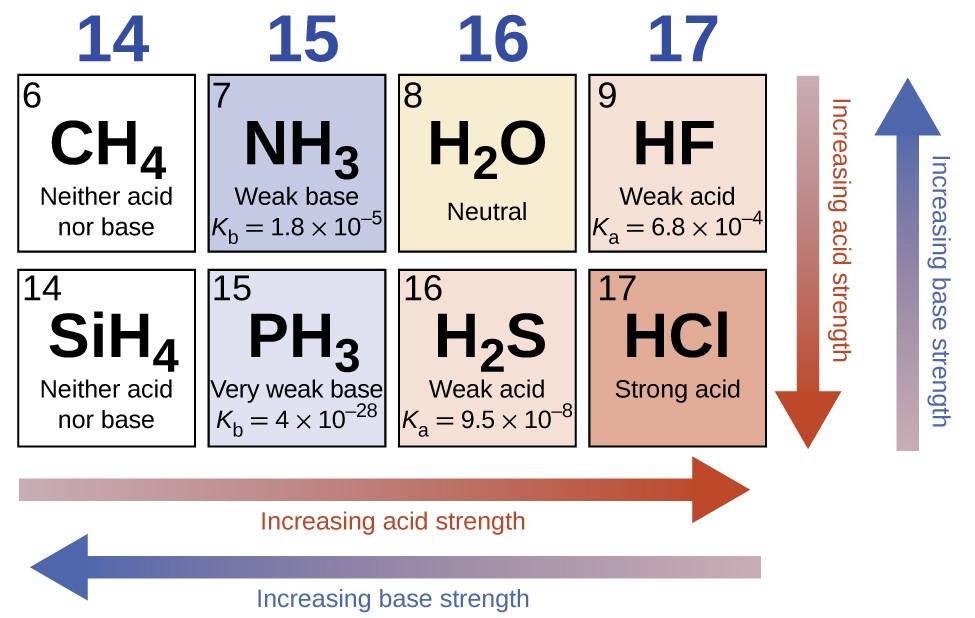
Figure 5.3.8. En se déplaçant de gauche à droite et en descendant dans le tableau périodique, la force de l’acide augmente. En allant de droite à gauche et vers le haut, la force de base augmente. 

Les composés contenant de l’oxygène et un ou plusieurs groupes hydroxyle (OH) peuvent être acides, basiques ou amphotères, selon la position dans le tableau périodique de l’atome central E, l’atome lié au groupe hydroxyle. Ces composés ont la formule générale O_nE(OH)_m, et comprennent l’acide sulfurique, O₂S(OH)₂, l’acide sulfureux, O_S(OH)₂, l’acide nitrique, O₂NOH, l’acide perchlorique, O₃ClOH, l’hydroxyde d’aluminium, Al(OH)₃, l’hydroxyde de calcium, Ca(OH)_2, et l’hydroxyde de potassium, KOH : 

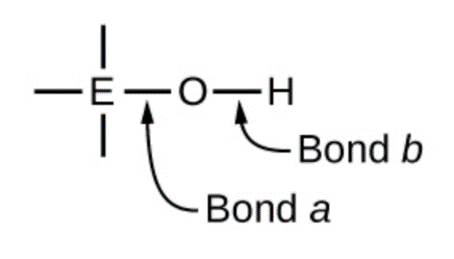
L’électronégativité des atomes et sa relation avec le caractère de liaison est examinée en détail dans la section 9.1, mais brièvement : l’électronégativité est une mesure de la capacité d’un atome à attirer les électrons de liaison vers son noyau. La nature de la liaison chimique entre deux atomes (X-Y) est directement corrélée à la différence d’électronégativité entre les deux atomes, c’est-à-dire ∆EN_XY = |ENX – ENY|. Une faible valeur de ∆EN_XY se traduit par une liaison chimique essentiellement covalente – les électrons sont partagés de manière égale par les deux atomes. Une valeur élevée de ∆EN_XY entraîne une liaison chimique de nature principalement ionique – la densité électronique n’est pas répartie de manière égale et le clivage de la liaison créera probablement un cation et un anion. 

Si l’on se réfère au schéma ci-dessus, l’atome d’O a une valeur EN élevée. Si l’atome central, E, a une faible électronégativité, alors ∆EN_EO est grand et l’atome central a tendance à former une liaison à caractère ionique plus importante avec l’atome d’oxygène. Par conséquent, la liaison a entre l’élément et l’oxygène est plus facilement rompue que la liaison b entre l’oxygène et l’hydrogène. Ainsi, la liaison a est ionique, les ions hydroxyde sont libérés dans la solution et le matériau se comporte comme une base – c’est le cas du Ca(OH)₂ et du KOH. Une électronégativité plus faible est caractéristique des éléments les plus métalliques ; ainsi, les éléments métalliques forment des hydroxydes ioniques qui sont par définition des composés basiques. 

Si, en revanche, l’atome E a une électronégativité relativement élevée, _∆ENEO est faible, et l’atome E partage les électrons de liaison à égalité avec l’atome d’oxygène, ce qui fait que la liaison est relativement fortement covalente. En comparaison, la liaison oxygène-hydrogène, la liaison b, a un caractère ionique plus important et est beaucoup plus polaire. En conséquence, la liaison O-H est plus facilement rompue et libère des ions hydrogène dans la solution, de sorte que le matériau se comporte comme un acide. Des électronégativités élevées sont caractéristiques des éléments les plus non métalliques. Ainsi, les éléments non métalliques forment des composés covalents contenant des groupes -OH acides, connus sous le nom d’oxoacides. 

L’augmentation de l’état d’oxydation de l’atome central E augmente également l’acidité d’un oxyacide car cela augmente l’attraction de E pour les électrons qu’il partage avec l’oxygène. Cette polarisation de la densité des électrons affaiblit la liaison O-H, ce qui facilite l’ionisation. Par exemple, l’acide sulfurique, H2SO4, ou O₂S(OH)₂ (avec un indice d’oxydation du soufre de +6), est plus acide que l’acide sulfureux, H₂SO₃, ou OS(OH)₂ (avec un indice d’oxydation du soufre de +4). De même, l’acide nitrique, HNO₃, ou O₂NOH (indice d’oxydation du N = +5), est plus acide que l’acide nitreux, HNO₂, ou ONOH (indice d’oxydation du N = +3). Dans chacune de ces paires, l’indice d’oxydation de l’atome central est plus élevé pour l’acide le plus fort (figure 5.3.9.). 

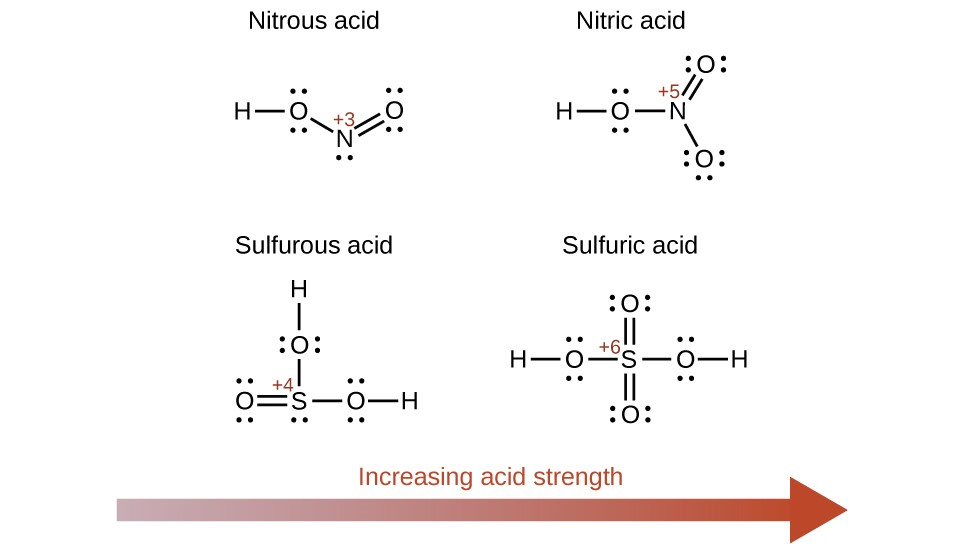
Figure 5.3.9. À mesure que le nombre d’oxydation de l’atome central E augmente, l’acidité augmente également. 

Les composés hydroxylés d’éléments ayant une électronégativité intermédiaire et un nombre d’oxydation relativement élevé (par exemple, les éléments situés près de la diagonale séparant les métaux des non-métaux dans le tableau périodique) sont généralement amphotères. Cela signifie que les composés hydroxylés agissent comme des acides lorsqu’ils réagissent avec des bases fortes et comme des bases lorsqu’ils réagissent avec des acides forts. L’amphotérisme de l’hydroxyde d’aluminium, qui existe généralement sous la forme de l’hydrate Al(H₂O)₃(OH)₃, se reflète dans sa solubilité à la fois dans les acides forts et les bases fortes. Dans les bases fortes, l’hydroxyde d’aluminium hydraté relativement insoluble, Al(H₂O)₃(OH)₃, est converti en ion soluble, [Al(H₂O)₂(OH)₄]⁻, par réaction avec l’ion hydroxyde : 

Al(H₂O)₃(OH)₃ (aq) + OH^– (aq) ⇌ H₂O (l) + [Al(H₂O)₂(OH)₄]^– (aq)

Dans cette réaction, un proton est transféré d’une des molécules H2O liées à l’aluminium à un ion hydroxyde en solution. Le composé Al(H2O)3(OH)3 agit donc comme un acide dans ces conditions. D’autre part, lorsqu’il est dissous dans des acides forts, il est converti en ion soluble [Al(H2O)6]3+ par réaction avec l’ion hydronium : 

3H₃O⁺ (aq) + Al(H₂O)₃(OH)₃ (aq) ⇌ Al(H₂O)₆³⁺ (aq) + 3H₂O (l)

Dans ce cas, les protons sont transférés des ions hydronium en solution à Al(H₂O)₃(OH)₃ et le composé fonctionne comme une base. 

Questions

★ Questions

1. Expliquez pourquoi la réaction de neutralisation d’un acide fort et d’une base faible donne une solution faiblement acide. 

2. Utilisez cette liste de composés industriels importants (et la figure 5.3.3.) pour répondre aux questions suivantes concernant : CaO, Ca(OH)₂, CH₃CO₂H, CO₂, HCl, H₂CO₃, HF, HNO₂, HNO₃, H₃PO₄, H₂SO₄, NH₃, NaOH, Na₂CO₃.

(a) Identifier les acides Brønsted-Lowry forts et les bases Brønsted-Lowry fortes. 

(b) Énumérer les composés en (a) qui peuvent se comporter comme des acides de Brønsted-Lowry avec des concentrations comprises entre celles de H₃O⁺ et H₂O. 

(c) Énumérer les composés en (a) qui peuvent se comporter comme des bases de Brønsted-Lowry avec des teneurs comprises entre celles de H₂O et de OH^–. 

3. L’odeur du vinaigre est due à la présence d’acide acétique, CH₃CO₂H, un acide faible. Énumérer, par ordre de concentration décroissante, toutes les espèces ioniques et moléculaires présentes dans une solution aqueuse de cet acide à 1 M. 

4. L’ammoniac domestique est une solution de la base faible NH₃ dans l’eau. Énumérer, par ordre de concentration décroissante, toutes les espèces ioniques et moléculaires présentes dans une solution aqueuse 1-M de cette base. 

5. Expliquez pourquoi la constante d’ionisation, K_a, pour H₂SO₄ est plus grande que la constante d’ionisation pour _H2SO3. 

6. Le suc gastrique, le liquide digestif produit dans l’estomac, contient de l’acide chlorhydrique, HCl. Le lait de magnésie, une suspension de Mg(OH)₂ solide dans un milieu aqueux, est parfois utilisé pour neutraliser l’excès d’acide gastrique. Écrivez une équation équilibrée complète pour la réaction de neutralisation et identifiez les paires conjuguées acide-base. 

7. L’acide nitrique réagit avec l’oxyde de cuivre(II) insoluble pour former du nitrate de cuivre(II) soluble, Cu(NO₃)₂, un composé qui a été utilisé pour empêcher la croissance des algues dans les piscines. Écrivez l’équation chimique équilibrée pour la réaction d’une solution aqueuse de HNO₃ avec CuO. 

8. Quelle est la constante d’ionisation à 25 °C pour l’acide faible CH₃NH₃⁺, l’acide conjugué de la base faible CH₃NH₂, K_b= 4,4 × 10^-11 ? 

9. Quel est l’acide le plus fort, NH₄⁺ ou HBrO ? 

10. Quelle est la base la plus forte, (CH₃)₃N ou H₂BO₃^– ? 

11. Prédisez quel composé de chacune des paires de composés suivantes est plus acide et expliquez votre raisonnement pour chacune d’entre elles. 

(a) HSO₄^– ou HSeO₄^–

(b) NH₃ ou H₂O

(c) PH₃ ou HI

(d) NH₃ ou PH₃

(e) H₂S ou HBr

12. Classez les composés dans chacun des groupes suivants par ordre d’augmentation de l’acidité ou de la basicité, comme indiqué, et expliquez l’ordre que vous leur attribuez. 

(a) Acidité: HCl, HBr, HI

(b) La basicité : H₂O, OH⁻, H⁻, Cl⁻ 

(c) La basicité : Mg(OH)₂, Si(OH)₄, ClO₃(OH)) (Conseil : la formule peut aussi s’écrire HClO₄). 

(d) acidité : HF, H₂O, NH₃, CH₄

13. Le HF et le HCN s’ionisent tous deux dans l’eau dans une mesure limitée. Laquelle des bases conjuguées, F^– ou CN^–, est la base la plus forte ? Voir les constantes d’ionisation des acides faibles pour résoudre ce problème. 

14. L’ingrédient actif formé par l’aspirine dans l’organisme est l’acide salicylique, _C6H4OH(_CO2H). Le groupe carboxyle (-CO2H) agit comme un acide faible. Le groupe phénol (un groupe OH lié à un cycle aromatique) agit également comme un acide, mais de manière beaucoup plus faible. Liste, par ordre de concentration décroissante, de toutes les espèces ioniques et moléculaires présentes dans une solution aqueuse de C₆H₄OH(CO₂H) à 0,001 M. 

15. Que représentons-nous lorsque nous écrivons : 

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O ⁺ (aq) + CH₃CO₂ ^– (aq)

Expliquer pourquoi les calculs d’équilibre ne sont pas nécessaires pour déterminer les concentrations ioniques dans les solutions de certains électrolytes forts tels que le NaOH et le HCl. Dans quelles conditions les calculs d’équilibre sont-ils nécessaires dans le cadre de la détermination des concentrations de tous les ions de certains autres électrolytes forts en solution ? 

16. Les concentrations d’ions hydronium et d’ions hydroxyde dans une solution d’un acide ou d’une base dans l’eau sont-elles directement proportionnelles ou inversement proportionnelles ? Expliquez votre réponse.

17. Quelles sont les deux hypothèses communes qui peuvent simplifier le calcul des concentrations d’équilibre dans une solution d’un acide faible ? 

18. Quelles sont les deux hypothèses communes qui peuvent simplifier le calcul des concentrations d’équilibre dans une solution d’une base faible ? 

19. Lequel des éléments suivants augmentera le pourcentage de NH3 qui est converti en ion ammonium dans l’eau (Indice : utiliser le principe de Le Châtelier.) ?

(a) ajout de NaOH

(b) ajout de HCl

(c) l’ajout de NH₄Cl

20. Laquelle des mesures suivantes permettra d’augmenter le pourcentage de HF qui est converti en ion fluorure dans l’eau ? 

(a) ajout de NaOH

(b) ajout de HCl

(c) ajout de NaF

21. Quel est l’effet sur les concentrations de NO₂^–, HNO₂, et OH^– lorsque les éléments suivants sont ajoutés à une solution de KNO₂ dans l’eau : 

(a) HCl

(b) HNO₂

(c) NaOH

(d) NaCl

(e) KNO

223. L’équation de l’équilibre est la suivante : 

NO₂ ^– (aq) + H₂O (l) ⇌ HNO₂ (aq) + OH ^– (aq)

Pourquoi la concentration d’ions hydronium dans une solution qui est de 0,10 M dans HCl et de 0,10 M dans HCOOH est-elle déterminée par la concentration de HCl ? 

23. À partir des concentrations d’équilibre données, calculer K_a pour chacun des acides faibles et K_b pour chacune des bases faibles. 

★★ Questions

25. Déterminez K_b pour l’ion nitrite, NO₂^–. Dans une solution de 0,10 M, cette base est ionisée à 0,0015 %. 

26. Déterminer K_a pour l’ion sulfate d’hydrogène, HSO₄^–. Dans une solution à 0,10 M, l’acide est ionisé à 29 %. 

27. Calculer la constante d’ionisation de chacun des acides ou bases suivants à partir de la constante d’ionisation de sa base conjuguée ou de son acide conjugué: 

(a) HTe^– (comme base)

(b) (CH₃)₃NH⁺

(c) HAsO₄^3-(comme base)

(d) HO₂^–(comme base)

(e) C₆H₅NH₃⁺

(f) HSO₃^– (comme base)

28. Pour laquelle des solutions suivantes devons-nous tenir compte de l’ionisation de l’eau lors du calcul du pH ou du pOH ? 

(a) 3 × 10^-8 M HNO₃

(b) 0,10 g de HCl dans 1,0 L de solution 

(c) 0,00080 g de NaOH dans 0,50 L de solution 

(d) 1 × 10^-7 M Ca(OH)₂

(e) 0,0245 M KNO₃

29. Calculer la concentration d’équilibre des acides et de tous les ions unionisés dans une solution qui est de 0,134 M dans le HNO₂ et de 0,120 M dans le HBrO. 

30. Calculer la concentration d’équilibre des bases unionisées et de tous les ions dans une solution qui est de 0,115 M dans NH₃ et de 0,100 M dans _C6H5NH2. 

31. L’acide propionique, C₂H₅CO₂H (K_a = 1,34 × 10^-5), est utilisé dans la fabrication du propionate de calcium, un conservateur alimentaire. Quelle est la concentration en ions hydronium dans une solution de C₂H₅CO₂H à 0,698 M ? 

32. Le pH d’une solution de HSO₄^– à 0,15 M est de 1,43. Déterminez le K_a du HSO₄^– à partir de ces données. 

33. Le pH d’une solution d’ammoniaque domestique, une solution de NH₃ à 0,950 M, est de 11,612. Déterminez le K_b pour le NH₃ à partir de ces données. 

Réponses

1. L’acide conjugué de la base faible utilisée provoque la solution légèrement acide.  Le sel s’ionise en solution, mais l’anion réagit légèrement avec l’eau pour former l’acide faible. Cette réaction forme également OH-^, ce qui rend la solution basique. 

2. (a) Ca(OH)₂, NH₃, NaOH, Na₂CO₃ ; (b) CH₃COOH, H₂CO₃, HF, HNO₂, H₃PO₄ ; (c) NH₃, Na₂CO₃

3. Les moles de

4. L’état d’oxydation du soufre dans le H₂SO₄ est supérieur à l’état d’oxydation du soufre dans le H₂SO₃. 

5. Mg(OH)₂ (s) + 2HCl (aq) ⇌ Mg²⁺ (aq) + 2Cl ^– (aq) + 2H₂O (l)

BB BA CB CA

6. CuO (s) + 2HNO₂ (l) ⇌ Cu(NO₃)₂ (l) + H₂O (l)

8. HBrO

9. Triéthylamine.

10. (a) HSO₄^– ; (b) H₂O; (c) HI; (d) PH₃ ;(e) HBr

11. (a) HCl < HBr < HI; (b) H₂O < Cl⁻ < H⁻ < OH⁻; (c) ClO₃(OH) < Si(OH)₄ < Mg(OH)₂; (d) CH₄ < NH₃ < H₂O < HF

12. CN^– est la base la plus solide.

14. C’est l’expression d’équilibre de la réaction acide-base entre l’acide acétique et l’eau pour former de l’acétate (base conjuguée) et de l’hydronium (acide conjugué), et vice-versa. 

15. Les électrolytes forts sont ionisés à 100%, et, tant que les ions constitutifs ne sont ni des acides faibles ni des bases faibles, les espèces ioniques présentes résultent de l’ionisation de l’électrolyte fort. Des calculs d’équilibre sont nécessaires lorsqu’un (ou plusieurs) des ions est un acide faible ou une base faible. 

16. Inversement proportionnel ; lorsqu’une concentration augmente, l’autre doit diminuer car K_w= [H+]⋅[OH-]=1.00×10^-14 doit rester une déclaration véridique. 

17. Supposons que le changement de la concentration initiale de l’acide au moment de l’établissement de l’équilibre puisse être négligé, de sorte que cette concentration puisse être considérée comme constante et égale à la valeur initiale de la concentration totale de l’acide. 2. Supposons que l’on puisse négliger la contribution de l’eau à la concentration d’équilibre de H₃O⁺. 

18. La [H⁺] avant l’ajout d’un acide ou d’une base (1.00×10^-7) est négligeable. 

19. La quantité d’acide ou de base faible qui s’ionise est négligeable.  

20. (a) L’ajout de HCl

(b) L’ajout de NaOH

21. (a) L’ajout de HCl ajoutera H₃O⁺ qui réagira ensuite avec les ions OH^–, en diminuant leur concentration. L’équilibre se déplacera vers la droite, augmentant la concentration de HNO₂ et en diminuant la concentration des ions NO₂^–. (b) Ajouter HNO₂ augmente la concentration de HNO₂ et déplace l’équilibre vers la gauche, augmentant la concentration de NO₂^– et en diminuant la concentration de OH^– ions. (c) L’ajout de NaOH ajout OH^– qui déplace l’équilibre vers la gauche, augmentant ainsi la concentration d’ions NO₂^– et en diminuant la concentration de HNO₂. (d) L’ajout de NaCl n’a aucun effet sur les concentrations des ions. (e) L’ajout de KNO₂ ajoute NO₂^– et déplace l’équilibre vers la droite, ce qui augmente la concentration des ions HNO₂ et OH^–. 

22. Il s’agit d’un cas où la solution contient un mélange d’acides de différentes forces d’ionisation. En solution, le HCO₂H existe principalement sous forme de molécules HCO₂H car l’ionisation de l’acide faible est supprimée par l’acide fort. Par conséquent, le HCO2H apporte une quantité négligeable d’ions hydronium à la solution. L’acide fort, HCl, est le producteur dominant d’ions hydronium car il est complètement ionisé. Dans une telle solution, l’acide fort détermine la concentration des ions hydronium, et l’ionisation de l’acide faible est fixée par le [H3O+] produit par l’acide fort. 

23. (a) K_b = 1.8 × 10^-5

(b) K_a = 4.5 × 10^-4

(c) K_b = 7.4 × 10^-5

(d) K_a = 5.6 × 10^-10

24. K_b = 4.44 × 10^-4

25. K_a = 1,2 × 10^-2

26. (a) K_b = 4.3 × 10^-12

(b) K_a = 1.6 × 10^-8

(c) K_b = 5.9 × 10^-7

(d) K_b = 4.2 × 10^-3

(e) K_b = 2.3 × 10^-3

(f) K_b = 6.3 × 10^-13

27. A et D

28. [H₃O⁺] = 7.5 × 10⁻³ M, [HNO₂] = 0.127, [OH⁻] = 1.3 × 10⁻¹² M, [BrO⁻] = 4.5 × 10⁻⁸ M, [HBrO] = 0.120 M

29. [NH₃]=0.144M

[H₃O⁺]=6.9×10^-12M

[C₆H₅NH₃⁺]=3.9×10^-8M

[C₆H₅NH₂]=0.100M

30. pH = 2,51

31. K_a = 1.2 × 10^-2

32. K_b = 1.77 × 10^-5