5.2 – Autoionisation de l’eau & pH/pOH

L’autoionisation de l’eau 

Dans la section précédente, nous avons vu des exemples où l’eau peut fonctionner soit comme un acide, soit comme une base, selon la nature du soluté qui y est dissous. En fait, dans l’eau pure ou dans toute solution aqueuse, l’eau agit à la fois comme un acide et comme une base. Une très petite fraction des molécules d’eau donne des protons à d’autres molécules d’eau pour former des ions hydroniums et des ions hydroxyde : 

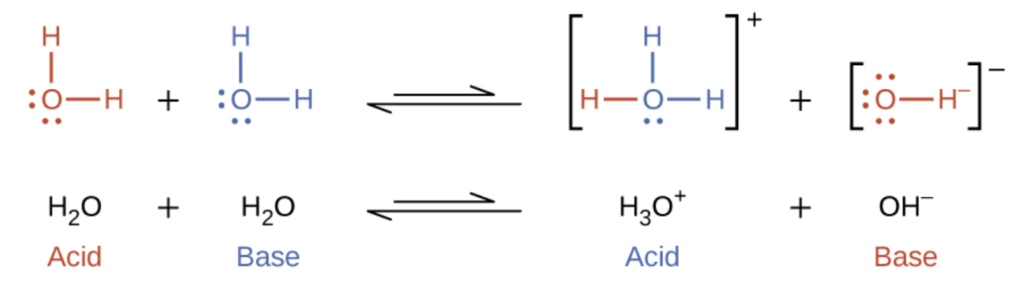
Ce type de réaction, dans lequel une substance s’ionise lorsqu’une molécule de la substance réagit avec une autre molécule de la même substance, est appelé autoionisation. 

L’eau pure subit une très légère autoionisation. Seules deux molécules sur un milliard (¹⁰⁹) dans un échantillon d’eau pure sont ionisées à 25 °C. La constante d’équilibre pour l’ionisation de l’eau est appelée constante ion-produit pour l’eau (KW) : 

H₂O (l) + H₂O (l) ⇌ H₃O⁺ (aq) + OH^– (aq)     K_w = [H₃O⁺][OH^–]

La légère ionisation de l’eau pure se reflète dans la faible valeur de la constante d’équilibre ; à 25 °C, le KW a une valeur de 1,0 × 10^-14. Le processus est endothermique, de sorte que l’étendue de l’ionisation et les concentrations d’ions hydronium et d’ions hydroxyde qui en résultent augmentent avec la température. Par exemple, à 100 °C, la valeur de Kw est d’environ 5,6 × 10-13, soit environ 50 fois plus que la valeur à 25 °C. 

Exemple 5.2.1  – Concentrations d’ions dans l’eau pure 

Quelle est la concentration en ions hydronium et en ions hydroxyde dans l’eau pure à 25 °C ? 

Solution 

L’autoionisation de l’eau produit le même nombre d’ions hydronium et hydroxyde. Par conséquent, dans l’eau pure, [H3O+] = [OH-]. À 25 °C : 

K_w =[H₃O⁺][OH^–] = [H₃O⁺]² = [OH^–]² = 1.0×10^-14

Donc : 

[H₃O⁺] = [OH-] = sqrt( 1.0×10^-14 ) =1.0×10^-7 M

La concentration d’ions hydronium et la concentration d’ions hydroxyde sont identiques, et nous constatons que les deux sont égales à 1,0 × 10-7 M. 

Vérifiez votre apprentissage 5.2.1  – Concentrations d’ions dans l’eau pure 

Le produit ionique de l’eau à 80 °C est de 2,4 × 10-13. Quelles sont les concentrations en ions hydronium et hydroxyde dans l’eau pure à 80 °C ? 

Réponse 

[H₃O⁺] = [OH⁻] = 4.9 × 10⁻⁷ M

Il est important de réaliser que l’équilibre d’autoionisation pour l’eau est établi dans toutes les solutions aqueuses. L’ajout d’un acide ou d’une base à l’eau ne modifie pas la position de l’équilibre. L’exemple suivant démontre les aspects quantitatifs de cette relation entre les concentrations d’ions hydronium et d’hydroxyde. 

Exemple 5.2.2 – La proportionnalité inverse de [H₃O⁺] et [OH⁻]

Une solution de dioxyde de carbone dans l’eau à l’équilibre a une concentration d’ions hydronium de 2.0 × 10^-6 M. Quelle est la concentration d’ions hydroxyde à 25 °C ? 

Solution 

Nous connaissons la valeur de la constante des produits ioniques pour l’eau à 25 °C : 

2 H₂O(l)↔ H3O⁺ (aq) + OH^– (aq)            K_w =[H₃O⁺][OH^–] = 1.0×10^-14

Ainsi, nous pouvons calculer la concentration d’équilibre manquante. 

Le réarrangement de l’expression Kw donne que [OH-] est directement proportionnel à l’inverse de [H3O+] : 

[OH^–] = K_w[H₃O⁺] = (1.0×10^-14)(2.0×10^-6 M) = 5.0×10^-9 M 

La concentration d’ions hydroxyde dans l’eau est réduite à 5,0 × 10^-9 M lorsque la concentration d’ions hydronium augmente à 2,0 × 10^-6 M. C‘est ce que prévoit le principe de Le Châtelier ; la réaction d’autoionisation se déplace vers la gauche pour réduire le stress de la concentration accrue d’ions hydronium et le [OH-] est réduit par rapport à celui de l’eau pure. Ceci est mieux visualisé avec une analogie de bascule, comme le montre la figure 5.2.1. 

Une vérification de ces concentrations confirme que notre arithmétique est correcte : 

K_w = [H₃O⁺][OH^–] = (2.0×10^-6 M)(5.0×10^-9 M) = 1.0×10^-14

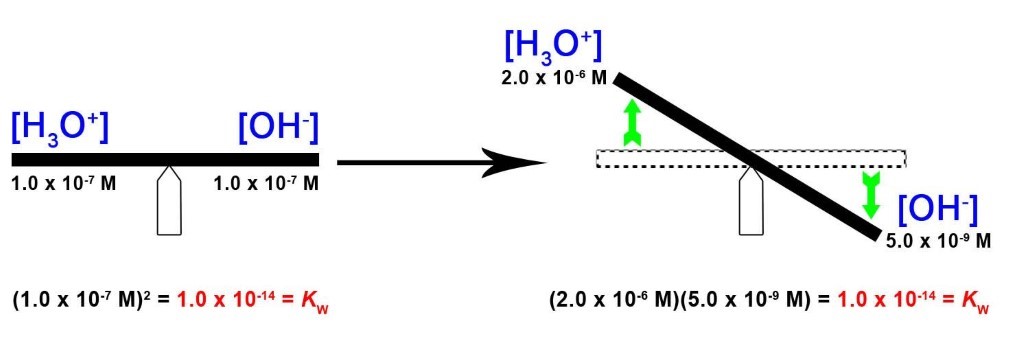
Figure 5.2.1. La constante de produit ionique est KW = 1,0 × 10^-14 tout le temps à 25°C. Dans l’eau pure, [H3O+] = [OH-] = 1,0 × 10^-7. Lorsque nous augmentons [H3O+], comme une bascule, cela est équilibré et contrebalancé par une diminution de [OH-] – cela maintient KW constant. 

Vérifiez votre apprentissage 5.2.2  – La proportionnalité inverse de [H₃O⁺] et [OH⁻]

Quelle est la concentration en ions hydronium dans une solution aqueuse dont la concentration en ions hydroxyde est de 0,001 M à 25 °C ? 

Réponse 

[H₃O⁺] = 1 × 10⁻¹¹ M

Espèces amphiprotiques 

Comme l’eau, de nombreuses molécules et de nombreux ions peuvent soit gagner, soit perdre un proton dans les conditions appropriées. Ces espèces sont dites amphiprotiques. Un autre terme utilisé pour décrire ces espèces est amphotère, qui est un terme plus général pour une espèce qui peut agir soit comme un acide soit comme une base selon n’importe quelle définition (pas seulement celle de Brønsted-Lowry). Prenons par exemple l’ion bicarbonate, qui peut soit donner soit accepter un proton comme indiqué ici : 

HCO₃⁻ (aq) + H₂O (l) ⇌ CO₃^2- (aq) + H₃O⁺ (aq)

HCO₃⁻ (aq) + H₂O (l) ⇌ H₂CO₃ (aq) + OH^– (aq)

Exemple 5.2.3  – Représentation du comportement acido-basique d’une substance amphotère 

Écrire des équations séparées représentant la réaction du HSO3- 

(a) agissant comme un acide avec OH- 

(b) agir en tant que base avec HI 

Solution

HSO₃⁻ (aq) + OH^– (aq) ⇌ SO₃^2- (aq) + H₂O (l)

HSO₃⁻ (aq) + HI (aq) ⇌ H₂SO₃ (aq) + I⁻ (aq)

Vérifiez votre apprentissage 5.2.3   – Représentation du comportement acido-basique d’une substance amphotère 

Écrire des équations séparées représentant la réaction de H2PO4- 

(a) comme base avec le HBr 

(b) sous forme d’acide avec OH- 

Réponse

H₂PO₄⁻ (aq) + HBr (aq) ⇌ H₃PO₄ (aq) + Br⁻ (aq)

H₂PO₄⁻ (aq) + OH⁻ (aq) ⇌ HPO₄^2- (aq) + H₂O (l)

pH et pOH 

Comme nous l’avons vu précédemment, les ions hydroniums et hydroxydes sont présents à la fois dans l’eau pure et dans toutes les solutions aqueuses, et leurs concentrations sont inversement proportionnelles, comme le montre le produit ionique de l'eau (Kw). Les concentrations de ces ions dans une solution sont souvent des déterminants critiques des propriétés de la solution et des comportements chimiques de ses autres solutés, et un vocabulaire spécifique a été développé pour décrire ces concentrations en termes relatifs. Une solution est neutre si elle contient des concentrations égales d’ions hydroniums et d’ions hydroxydes, acide si elle contientune plus grande concentration d’ions hydronium que d’ions hydroxyde, et basique si elle contient une concentration moindre d’ions hydronium que d’ions hydroxyde. 

Un moyen courant d’exprimer des quantités, dont les valeurs peuvent couvrir plusieurs ordres de grandeur, consiste à utiliser une échelle logarithmique. Une telle échelle, très populaire pour les concentrations chimiques et les constantes d’équilibre, est basée sur la fonction p, définie comme suit : “X” est la quantité d’intérêt et “log” est le logarithme de base 10 : 

pX = -log(X)

Le pH d’une solution est donc défini comme indiqué ici, où [H₃O⁺] est la concentration molaire de l’ion hydronium dans la solution : 

pH =-log[H₃O⁺]

En réorganisant cette équation pour isoler la molarité de l’ion hydronium, on obtient l’expression équivalente : 

[H₃O⁺]= 10^-pH

De même, la molarité de l’ion hydroxyde peut être exprimée par une fonction p, ou pOH : 

pOH = -log[OH^–]

ou  

[OH^–] = 10^-pOH

Enfin, la relation entre ces deux concentrations d’ions exprimées sous forme de p-fonctions est facilement dérivée de l’expression Kw : 

K_w =[H₃O⁺][OH^–]

-log(K_w) =-log([H₃O⁺][OH^–])= -log[H₃O⁺]+-log[OH^–]

pK_w=pH+pOH

À 25 °C, la valeur de K_w est de 1,0 × 10^-14, et donc : 

14.00 = pH + pOH 

Comme l’a montré la réaction d’un acide de Brønsted-Lowry avec l’eau, la molarité de l’ion hydronium dans l’eau pure (ou toute solution neutre) est de 1.0 × 10^-7 M à 25 °C. Le pH et le pOH d’une solution neutre à cette température sont donc de 1.0 × 10^-7 M à 25 °C : 

pH=-log[H₃O⁺]=-log(1.0×10^-7)=7.00

pOH=-log[OH-]=-log(1.0×10^-7)=7.00

Ainsi, à cette température, les solutions acides sont celles dont les molarités des ions hydronium sont supérieures à 1,0 × 10^-7 M et celles des ions hydroxyde inférieures à 1,0 × 10^-7 M (correspondant à des valeurs de pH inférieures à 7,00 et des valeurs de pOH supérieures à 7,00). Les solutions basiques sont celles dont les molarités des ions hydronium sont inférieures à 1.0 × 1010^-7 M et les molarités des ions hydroxyde supérieures à 1,0 × 10^-7 M (correspondant à des valeurs de pH supérieures à 7,00 et des valeurs de pOH inférieures à 7,00). 

Comme la constante d’autoionisation Kw dépend de la température, ces corrélations entre les valeurs de pH et les adjectifs acide, neutre et basique seront différentes à des températures autres que 25 °C (figure 5.2.2). Par exemple, l’exercice “Vérifiez votre apprentissage” du sujet précédent a montré que la molarité de l’hydronium de l’eau pure à 80 °C est de 4,9 × 10^-7 M, ce qui correspond aux valeurs de pH et de pOH de : 

pH = -log[H₃O⁺] = -log(4.9×10^-7) = 6.31

pOH=-log[OH^–] = -log(4.9×10^-7) = 6.31

À cette température, les solutions neutres présentent donc un pH = pOH = 6,31, les solutions acides un pH inférieur à 6,31 et un pOH supérieur à 6,31, tandis que les solutions basiques présentent un pH supérieur à 6,31 et un pOH inférieur à 6,31. Cette distinction peut être importante pour l’étude de certains processus qui se produisent à des températures non standard, comme les réactions enzymatiques dans les organismes à sang chaud. 

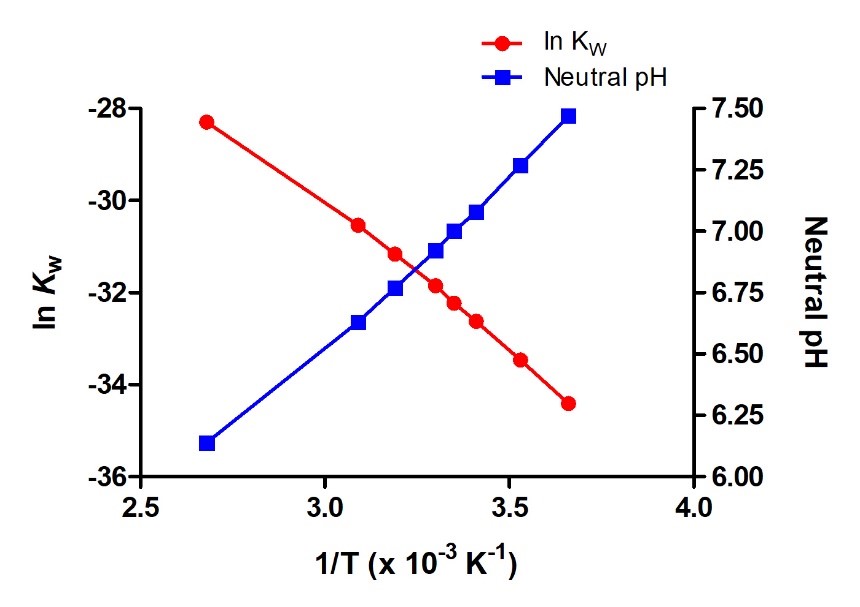
Figure 5.2.2. Comme toute autre constante d’équilibre, la constante d’autoionisation, K_W, dépend de la température. On peut donc construire un diagramme de van’t Hoff pour voir la variation de K_W en fonction de T. Le graphique représente également la variation du pH de l’eau pure neutre en fonction de la température. 

Sauf indication contraire, les références aux valeurs de pH, telles que celles du tableau 5.2.1 ci-dessous, sont présumées être celles à la température standard (25 °C). 

Tableau 5.2.1 Résumé des relations pour les solutions acides, basiques et neutres 

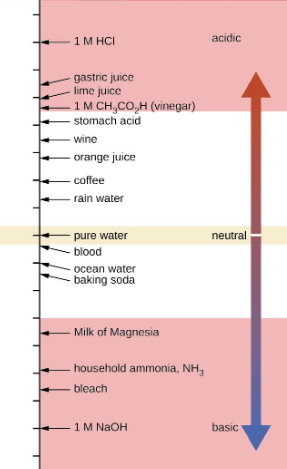
Figure 5.2.2. Les échelles de pH et de pOH représentent les concentrations de H₃O⁺ et de OH^–, respectivement. Les valeurs de pH et de pOH de certaines substances courantes à température standard (25 °C) sont indiquées dans ce tableau.

Exemple 5.2.4  – Calcul du pH à partir de [H₃O⁺]

Quel est le pH de l’acide gastrique, une solution de HCl ayant une concentration en ions hydronium de 1,2 × 10^-3 M ? 

Solution

(L’utilisation des logarithmes est expliquée à l’annexe C. Rappelez-vous que, comme nous l’avons fait ici, lorsque vous prenez le logarithme d’une valeur, gardez autant de décimales dans le résultat qu’il y a de chiffres significatifs dans la valeur). 

Vérifiez votre apprentissage 5.2.4  – Calcul du pH à partir de [H₃O⁺]

L’eau exposée à l’air contient de l’acide carbonique, H₂CO₃, dû à la réaction entre le dioxyde de carbone et l’eau : 

CO₂ (aq) + H₂O (l) ⇌ H₂CO₃ (aq)

L’eau saturée en air a une concentration en ions hydronium due au CO₂ dissous de 2,0 × 10^-6 M, soit environ 20 fois plus que celle de l’eau pure. Calculez le pH de la solution à 25 °C. 

Réponse 

5.70 

Exemple 5.2.4 – Calcul de la concentration d’ions hydronium à partir du pH 

Calculez la concentration en ions hydronium du sang, dont le pH est de 7,3 (légèrement alcalin). 

Solution 

pH= -log[H₃O⁺] = 7.3

log[H₃O⁺]= -7.3

[H₃O⁺] = 10^-7.3 or[H3O+] =antilog of -7.3

[H₃O⁺] = 5×10^-8 M

(Sur une calculatrice, prenez l’antilog, ou le log “inverse”, de -7,3; ou calculez 10^-7,3). 

Vérifiez votre apprentissage 5.2.4 – Calcul de la concentration d’ions hydronium à partir du pH 

Calculer la concentration en ions hydronium d’une solution dont le pH est de -1,07. 

Réponse 

12 M 

Science de l’environnement 

L’eau de pluie normale a un pH compris entre 5 et 6 en raison de la présence de CO₂ dissous qui forme de l’acide carbonique : 

H₂O (l) + CO₂ (g) ⇌ H₂CO₃ (aq)

H₂CO₃ (aq) + H₂O(l) ⇌ HCO₃^– (aq) + H₃O⁺ (aq)

Les pluies acides sont des eaux de pluie dont le pH est inférieur à 5, en raison de la dissolution dans l’eau de divers oxydes non métalliques, dont le CO2, le SO2, le SO3, le NO et le NO2, qui réagissent avec l’eau pour former non seulement de l’acide carbonique, mais aussi de l’acide sulfurique et de l’acide nitrique. La formation et l’ionisation ultérieure de l’acide sulfurique sont illustrées ici : 

H₂O(l) + SO₃(g) → H₂SO₄(aq)

H₂SO₄(aq) + H₂O(aq) → HSO₄^–(aq) + H₃O⁺(aq)

Le dioxyde de carbone est naturellement présent dans l’atmosphère parce que nous et la plupart des autres organismes le produisons comme un déchet du métabolisme. Le dioxyde de carbone se forme également lorsque les incendies libèrent le carbone stocké dans la végétation ou lorsque nous brûlons du bois ou des combustibles fossiles. Le trioxyde de soufre dans l’atmosphère est naturellement produit par l’activité volcanique, mais il provient également de la combustion de combustibles fossiles, qui présentent des traces de soufre, et du processus de “grillage” de minerais de sulfures métalliques dans les procédés d’affinage des métaux. Les oxydes d’azote se forment dans les moteurs à combustion interne où les températures élevées permettent à l’azote et à l’oxygène de l’air de se combiner chimiquement. 

Les pluies acides constituent un problème particulier dans les zones industrielles où les produits de la combustion et de la fusion sont rejetés dans l’air sans être débarrassés des oxydes de soufre et d’azote. En Amérique du Nord et en Europe, jusqu’aux années 1980, elles étaient responsables de la destruction des forêts et des lacs d’eau douce, alors que l’acidité des pluies tuait en fait les arbres, endommageait les sols et rendait les lacs inhabitables pour toutes les espèces sauf les plus tolérantes à l’acidité. Les pluies acides corrodent également les façades des statues et des bâtiments en marbre et en pierre calcaire (figure 5.2.3.). Les réglementations limitant la quantité d’oxydes de soufre et d’azote pouvant être rejetée dans l’atmosphère par l’industrie et les automobiles ont réduit la gravité des dommages causés par l’acide aux environnements naturels et artificiels en Amérique du Nord et en Europe. C’est maintenant un problème croissant dans les zones industrielles de Chine et d’Inde. 

Si ce sujet vous intéresse et que vous souhaitez en savoir plus sur ce sujet et/ou sur d’autres sujets environnementaux et leur relation avec la chimie, le département de chimie et de sciences biomoléculaires de la faculté des sciences propose le cours CHM 2713 : Chimie environnementale au semestre d’hiver. 

Figure 5.2.3. (a) Les pluies acides rendent les arbres plus sensibles à la sécheresse et aux infestations d’insectes, et épuisent les éléments nutritifs du sol. (b) Elles corrodent également les statues qui sont sculptées dans le marbre ou le calcaire. (Crédit a : modification du travail de Chris M Morris ; crédit b : modification du travail de “Eden, Janine et Jim”/Flickr) 

Exemple 5.2.5  – Calcul du pOH 

Quels sont le pOH et le pH d’une solution 0,0125-M d’hydroxyde de potassium, KOH ? 

Solution 

L’hydroxyde de potassium est un composé ionique très soluble qui s’ionise complètement lorsqu’il est dissous dans une solution diluée, ce qui donne [OH^–] = 0,0125 M : 

pOH =-log[OH^–] = -log(0.0125)

= -(-1.903)=1.903

Le pH peut être trouvé à partir du pOH : 

pH+pOH = 14.00

pH= 14.00-pOH = 14.00-1.903 =12.10

Vérifiez votre apprentissage 5.2.5  – Calcul du pOH 

La concentration en ions hydronium du vinaigre est d’environ 4 × 10^-3 M. Quelles sont les valeurs correspondantes de pOH et de pH ? 

Réponse  

pOH = 11,6, pH = 2,4 

L’acidité d’une solution est généralement évaluée expérimentalement par la mesure de son pH. Le pOH d’une solution n’est généralement pas mesuré, car il est facilement calculé à partir d’une valeur de pH déterminée expérimentalement. La manière la plus précise de déterminer le pH d’une solution acide est le titrage. Le deuxième outil le plus efficace est la mesure directe à l’aide d’un pH-mètre (figure 5.2.4.). 

Figure 5.2.4. a) Un pH-mètre de qualité recherche utilisé dans un laboratoire peut avoir une résolution de 0,001 unité de pH, une précision de ± 0,002 unité de pH et peut coûter plus de 1 000 dollars. b) Un pH-mètre portable a une résolution plus faible (0,01 unité de pH), une précision plus faible (± 0,2 unité de pH) et un prix beaucoup plus bas. (crédit b : modification du travail de Jacopo Werther) 

Le pH d’une solution peut également être estimé visuellement à l’aide d’indicateurs colorés (figure 5.2.5.), qui sont les moins précis dans la détermination du pH. 

Figure 5.2.5. (a) Un indicateur universel prend une couleur différente dans des solutions de pH différents. Ainsi, il peut être ajouté à une solution pour déterminer le pH de la solution. Les huit flacons contiennent chacun un indicateur universel et des solutions 0,1-M d’acides progressivement plus faibles : HCl (pH = l), CH₃CO₂H (pH = 3), et NH₄Cl (pH = 5), de l’eau déionisée, une substance neutre (pH = 7) ; et des solutions 0,1-M de bases progressivement plus fortes : KCl (pH = 7), aniline, C₆H₅NH₂ (pH = 9), NH3 (pH = 11), et NaOH (pH = 13). (b) Le papier pH contient un mélange d’indicateurs qui donnent des couleurs différentes dans des solutions de pH différents. (crédit: modification du travail de Sahar Atwa)

Questions

★ Questions

1. Quelle est la relation entre [H⁺] et K_w ? Écrivez une expression mathématique qui les relie 
2. Écrivez l’équation chimique pour l’autoionisation de l’eau et marquez les paires acide-base conjuguées. 
3. Si le HNO₂ n’est ionisé qu’à hauteur de 0,445 %, que sont [H⁺] et [OH^–] dans une solution de HNO2 à 0,307 M ? 
4. Expliquez pourquoi un échantillon d’eau pure à 40 °C est neutre même si [H₃O⁺] = 1,7 × 10^-7 M. Le K_w est de 2,9 × 10^-14 à 40 °C. 
5. La constante d’ionisation de l’eau (Kw) est de 2,9 × 10^-14 à 40 °C. Calculer [H₃O⁺], [OH^–], pH et pOH pour de l’eau pure à 40 °C. 
6. La constante d’ionisation de l’eau (Kw) est de 9,311 × 10^-14 à 60 °C. Calculer [H₃O⁺], [OH^–], pH et pOH pour de l’eau pure à 60 °C. 
7. Calculez le pH et le pOH de chacune des solutions suivantes à 25 °C pour lesquelles les substances s’ionisent complètement : 

(a) 0,200 M HCl

(b) 0,0143 M NaOH

(c) 3,0 M HNO3

(d) 0,0031 M Ca(OH)₂

8. Calculez le pH et le pOH de chacune des solutions suivantes à 25 °C pour lesquelles les substances s’ionisent complètement : 

(a) 0,000259 M HClO4

(b) 0,21 M NaOH

(c) 0,000071 M Ba(OH)₂

(d) 2,5 M KOH

9. Quels sont le pH et le pOH d’une solution de HCl 2,0 M, qui s’ionise complètement ? 

10. Quelles sont les concentrations en ions hydronium et hydroxyde dans une solution dont le pH est de 6,52 ? 

11. Calculer la concentration d’ions hydrogène et la concentration d’ions hydroxyde dans le vin à partir de son pH. Voir la figure 5.2.2. pour des informations utiles.

12. Calculer la concentration d’ions hydronium et la concentration d’ions hydroxyde dans le jus de citron vert à partir de son pH. Voir la figure 5.2.2. pour des informations utiles.

13. La concentration en ions hydronium dans un échantillon d’eau de pluie est de 1,7 × 10^-6 M à 25 °C. Quelle est la concentration des ions hydroxyde dans l’eau de pluie ? 

14. La concentration d’ions hydroxyde dans l’ammoniac domestique est de 3,2 × 10^-3 M à 25 °C. Quelle est la concentration des ions hydronium dans la solution ? 

Réponses

1. [H⁺] = K_w[OH⁻]

2. H₂O + H₂O → H₃O⁺ + OH⁻; H₂O/H₃O⁺ et H₂O/OH⁻

3. [H⁺] = 0.00137 M; [OH⁻] = 7.32 × 10⁻¹² M

4. Dans une solution neutre [H₃O⁺] = [OH⁻]. At 40 °C, [H₃O⁺] = [OH⁻] = (2.910−14)*(1/2) = 1.7 × 10⁻⁷ M

5. [H₃O⁺] = [OH⁻] = 1.703 x 10⁻⁷ M, pOH = pH = 6.77

6. x = 3.051 × 10⁻⁷ M = [H₃O⁺] = [OH⁻], pH = −log(3.051) × 10⁻⁷ = −(−6.5156) = 6.5156, pOH = pH = 6.5156

7. (a) pH = 0.699, pOH = 13.3, (b) pH = 12.15, pOH = 1.85, (c) pH = -0.477, pOH = 14.5, (d) pH = 12.8, pOH = 1.2

8. (a) pH = 3.587; pOH = 10.413; (b) pH = 0.68; pOH = 13.32; (c) pOH = 3.85; pH = 10.15; (d) pH = −0.40; pOH = 14.4

9. pOH = 14.301, pH = -0.301

10. [H₃O⁺]= 3.0 × 10⁻⁷ M; [OH⁻] = 3.3 × 10⁻⁸ M

11. [H₃O⁺]= 3.162 x 10⁻⁴ M; [OH⁻] = 3.162 x 10⁻¹¹ M

12. [H₃O⁺]= 1 × 10⁻² M; [OH⁻] = 1 × 10⁻¹² M

13. [OH^–] = 5.9 × 10^-9 M

14. [OH⁻] = 3.1 × 10−12 M