4.3 – Résolution des problèmes d’équilibre

Nous savons qu’à l’équilibre, la valeur du quotient de réaction de toute réaction est égale à sa constante d’équilibre. Ainsi, nous pouvons utiliser l’expression mathématique de Q pour déterminer un certain nombre de quantités associées à une réaction à l’équilibre ou proche de l’équilibre. Si nous avons appris à identifier la direction dans laquelle une réaction va se déplacer pour atteindre l’équilibre, nous voulons étendre cette compréhension aux calculs quantitatifs. Nous le faisons en évaluant la façon dont les concentrations de produits et de réactifs changent lorsqu’une réaction s’approche de l’équilibre, en gardant à l’esprit les rapports stœchiométriques de la réaction. Cette approche algébrique des calculs d’équilibre sera explorée dans cette section.

Changements relatifs de la concentration

Les changements de concentration ou de pression des réactifs et des produits se produisent lorsqu’un système réactionnel s’approche de l’équilibre. Dans cette section, nous verrons que nous pouvons relier ces changements les uns aux autres en utilisant les coefficients de l’équation chimique équilibrée décrivant le système. Nous utilisons la décomposition de l’ammoniac comme exemple.

En chauffant, l’ammoniac se décompose de manière réversible en azote et en hydrogène selon cette équation :

2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g)

Si un échantillon d’ammoniac se décompose dans un système fermé et que la concentration de N₂ augmente de 0,11 mol/L, la variation de la concentration de N₂, Δ[N₂] = [N₂]_f – [N₂]_i, est de 0,11 M. La variation est positive car la concentration de N2 augmente.

La modification de la concentration en H2, Δ[_H2], est également positive – la concentration en _H2 augmente avec la décomposition de l’ammoniac. L’équation chimique nous dit que la variation de la concentration de _H2 est trois fois plus importante que celle de la concentration de N2 car pour chaque mole de N2 produite, 3 moles de _H2 sont produites.

[H₂] = 3 × [N₂]

= 3 × (0.11 mol/L) = 0.33 mol/L

Le changement de concentration de NH₃, Δ[NH₃], est deux fois plus important que celui de Δ[N₂] ; l’équation indique que 2 moles de NH₃ doivent se décomposer pour chaque mole de N₂ formée. Cependant, le changement de la concentration de NH₃ est négatif car la concentration d’ammoniac diminue au fur et à mesure de sa décomposition.

∆[NH₃] = – 2 × ∆[N₂] = – 2 × (0.11 mol/L) = – 0.22 mol/L

Nous pouvons relier ces relations directement aux coefficients de l’équation

2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g)

Notez que tous les changements d’un côté des flèches sont du même signe et que tous les changements de l’autre côté des flèches sont du signe opposé.

Si nous ne connaissions pas l’ampleur de la variation de la concentration de N2, nous pourrions la représenter par le symbole +x.

Les changements dans les autres concentrations seraient alors représentés comme :

∆[H₂] = 3 × ∆[N₂] = + 3x

∆[NH₃] = – 2 × ∆[N₂] = – 2x

Les coefficients des termes Δ sont identiques à ceux de l’équation équilibrée de la réaction.

La façon la plus simple pour nous de trouver les coefficients des changements de concentration dans une réaction est d’utiliser les coefficients de l’équation chimique équilibrée. Le signe du coefficient est positif lorsque la concentration augmente ; il est négatif lorsque la concentration diminue.

Exemple 4.3.1 – Déterminer les changements relatifs de la concentration

Complétez les changements de concentration pour chacune des réactions suivantes.

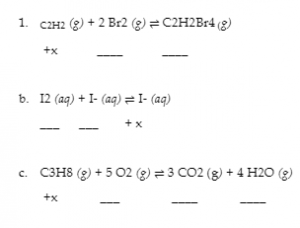
Solution

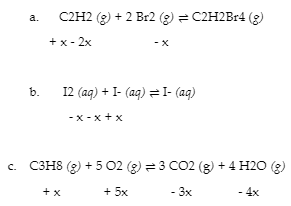
Vérifiez votre apprentissage 4.3.1

Complétez les changements de concentration pour chacune des réactions suivantes :

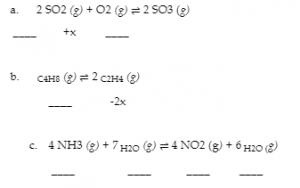
Réponse

(a) + 2x, + x, – 2x ; (b) + x, – 2x ; (c) + 4x, + 7x, – 4x, – 6x ou – 4x, – 7x, + 4x, + 6x

Calculs impliquant des concentrations ou des pressions à l’équilibre

Parce que la valeur du quotient de réaction de toute réaction à l’équilibre est égale à sa constante d’équilibre, nous pouvons utiliser l’expression mathématique de Q pour déterminer un certain nombre de quantités associées à une réaction à l’équilibre. Il peut être utile de garder à l’esprit que Q = K (à l’équilibre) dans toutes ces situations et qu’il n’existe que deux types de problèmes d’équilibre :

1. Calcul d’une constante d’équilibre. Si les concentrations/pressions partielles des réactifs et des produits à l’équilibre sont connues, la valeur de la constante d’équilibre pour la réaction peut être calculée.
2. Calcul des concentrations d’équilibre/pressions partielles. Si la valeur de la constante d’équilibre et toutes les concentrations / pressions d’équilibre, sauf une, sont connues, l’inconnue restante peut être calculée. En outre, si la valeur de la constante d’équilibre et un ensemble de concentrations ou de pressions de réactifs et de produits qui ne sont pas à l’équilibre sont connus, la quantité à l’équilibre peut être calculée.

Dans la discussion suivante, nous examinerons des exemples de calculs d’équilibre impliquant des solutés et des valeurs de K en unités de concentration (K_C). Cependant, veuillez noter que les procédures de résolution de problèmes s’appliquent également aux réactions impliquant des gaz et des valeurs de K en unités de pression (K_P).

Calcul d’une constante d’équilibre

Pour calculer une constante d’équilibre, il faut disposer de suffisamment d’informations pour déterminer les concentrations d’équilibre de tous les réactifs et produits. Grâce à ces concentrations, nous pouvons résoudre l’équation pour K, car ce sera la seule inconnue.

Dans la section précédente, nous avons appris comment déterminer la constante d’équilibre d’une réaction si nous connaissons les concentrations des réactifs et des produits à l’équilibre. L’exemple suivant montre comment utiliser la stœchiométrie de la réaction et une combinaison des concentrations initiales et des concentrations à l’équilibre pour déterminer une constante d’équilibre. Cette technique, communément appelée tableau ICE – pour Initial, Changement, and Équilibre – sera utile pour résoudre de nombreux problèmes d’équilibre. Un graphique est généré à partir de la réaction d’équilibre en question. Les concentrations initiales des réactifs et des produits sont indiquées dans la première ligne du tableau ICE (il s’agit essentiellement de concentrations nulles dans le temps qui supposent qu’aucune réaction n’a eu lieu). La ligne suivante du tableau contient les changements de concentrations qui se produisent lorsque la réaction se rapproche de l’équilibre (n’oubliez pas de tenir compte de la stœchiométrie de la réaction). La dernière ligne contient les concentrations une fois que l’équilibre a été atteint.

Exemple 4.3.2 – Calcul d’une constante d’équilibre – 1

Les molécules d’iode réagissent de manière réversible avec les ions iodure pour produire des ions triiodure.

I₂ (aq) + I- (aq) ⇌ I^3- (aq)

Si une solution dont les concentrations de I₂ et I- sont toutes deux égales à 1 000 × 10^-3 mol/L avant la réaction donne une concentration d’équilibre de I2 de 6,61 × 10^-4 mol/L, quelle est la constante d’équilibre de la réaction ?

Solution

Nous commencerons ce problème en calculant les changements de concentration au fur et à mesure que le système se rapproche de l’équilibre. Ensuite, nous déterminons les concentrations d’équilibre et, enfin, la constante d’équilibre. Tout d’abord, nous établissons un tableau avec les concentrations initiales, les changements de concentration et les concentrations d’équilibre en utilisant -x comme changement de concentration de I₂.

I₂ + I⁻⇌ I³⁻

Puisque la concentration de I2 à l’équilibre est donnée, nous pouvons résoudre x. À l’équilibre, la concentration de I² est donc de 6,61 × 10^-4 M:

1.000 × 10^-3 – x = 6.61 × 10^-4

x = 1.000 × 10^-3 – 6.61 × 10^-4

x = 3.39 × 10^-4 mol/L

Nous pouvons maintenant remplir le tableau avec les concentrations à l’équilibre.

I₂ + I⁻⇌ I³⁻

Nous calculons maintenant la valeur de la constante d’équilibre.

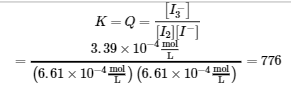
Cette valeur pour K est logique – elle est proche de 1, ce qui indique qu’à l’équilibre, le système contiendra des quantités comparables de réactifs et de produits. Cela est vrai lorsque l’on regarde la concentration à l’équilibre dans le tableau ICE, ou même que l’on visualise la proximité des courbes de concentration (dans un graphique) des espèces lorsque l’équilibre est atteint (figure 4.3.1).

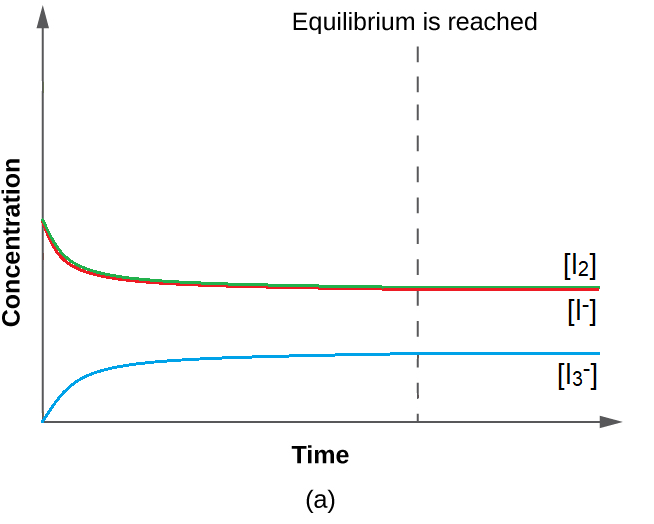
Figure 4.3.1. Avec une valeur de K relativement proche de 1, les concentrations des réactifs et des produits se rapprochent les unes des autres lorsque le système se rapproche de l’équilibre.

Vérifiez votre apprentissage 4.3.2 – Calcul d’une constante d’équilibre – 1

L’éthanol et l’acide acétique réagissent pour former de l’eau et de l’acétate d’éthyle, le solvant responsable de l’odeur de certains dissolvants de vernis à ongles :

C₂H₅OH + CH₃CO₂H ⇌ CH₃CO₂C₂H₅ + H₂O

Lorsqu’on laisse réagir 1,00 mol de C₂H₅OH et de CH₃CO₂H dans 1 L de dioxane, l’équilibre est établi lorsqu’il reste 0,13 mol de chacun des réactifs. Calculer la constante d’équilibre pour la réaction. (Remarque : l’eau n’est pas un solvant dans cette réaction).

Réponse

K_C = 45

Exemple 4.3.3 – Calcul d’une constante d’équilibre – 2

Un échantillon de 1,00 mol de NOCl a été placé dans un réacteur de 2,00 L et chauffé à 227°C jusqu’à ce que le système atteigne l’équilibre. Le contenu du réacteur a ensuite été analysé et on a constaté qu’il contenait 0,056 mol de Cl2. Calculer le KC à cette température. L’équation pour la décomposition de NOCl en NO et Cl2 est la suivante :

2 NOCl (g) ⇌ 2 NO (g) + Cl₂ (g)

Solution

La première étape de tout problème de ce type consiste à équilibrer l’équation chimique de la réaction (si elle n’est pas déjà équilibrée) et à l’utiliser pour dériver l’expression de la constante d’équilibre. Dans ce cas, l’équation est déjà équilibrée, et l’expression de la constante d’équilibre est la suivante :

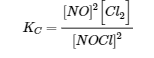
Au départ, le système contient 1,00 mol de NOCl dans un récipient de 2,00 L. Ainsi, [NOCl]_i = 1,00 mol/2,00 L = 0,500 mol/L. Les concentrations initiales de NO et de Cl₂ sont de 0 mol/L parce qu’initialement aucun produit n’est présent. De plus, on nous dit qu’à l’équilibre, le système contient 0,056 mol de Cl₂ dans un récipient de 2,00 L, donc [Cl₂]_{f =} 0,056 mol/2,00 L = 0,028 mol/L. Nous insérons ces valeurs dans le tableau suivant :

Nous utilisons les relations stœchiométriques données dans l’équation chimique équilibrée pour trouver la variation de la concentration de Cl₂, la substance dont les concentrations initiale et finale sont connues :

Δ [Cl₂] = [0,028 mol/L (final) – 0,00 mol/L (initial)] = + 0,028 mol/L

Selon les coefficients de l’équation chimique équilibrée, 2 mol de NO sont produites pour 1 mol de Cl₂, donc l’évolution de la concentration de NO est la suivante :

De même, 2 mol de NOCl sont consommées pour 1 mol de Cl₂ produite, donc l’évolution de la concentration de NOCl est la suivante :

Nous insérons ces valeurs dans notre tableau :

Nous additionnons les chiffres des colonnes [NOCl] et [NO] pour obtenir les concentrations finales de NO et de NOCl :

[NO]_f = 0,000 M + 0,056 M = 0,056 M

[NOCl]_f = 0,500 M + (-0,056 M) = 0,444 M

Nous pouvons maintenant compléter le tableau :

Nous pouvons maintenant calculer la constante d’équilibre de la réaction :

Vérifiez votre apprentissage 4.3.3 – Calcul d’une constante d’équilibre – 2

Le chimiste allemand Fritz Haber (1868-1934 ; prix Nobel de chimie 1918) a réussi à synthétiser de l’ammoniac (NH₃) en faisant réagir 0,1248 M H₂ et 0,0416 M N₂ à environ 500°C (figure 4.3.2). À l’équilibre, le mélange contenait 0,00272 M NH3. Quel est le K_C pour la réaction N₂ + 3 H₂ ⇌ 2 NH₃ à cette température ? Quelle est la valeur du K_P ?

Figure 4.3.2. L’appareil de laboratoire original conçu par Fritz Haber et Robert Le Rossignol en 1908 pour synthétiser l’ammoniac à partir de ses éléments. Un lit catalytique métallique, où l’ammoniac était produit, se trouve dans le grand cylindre à gauche. Le procédé Haber-Bosch utilisé pour la production industrielle d’ammoniac utilise essentiellement le même procédé et les mêmes composants, mais à une échelle beaucoup plus grande. Malheureusement, le procédé Haber a permis à l’Allemagne de prolonger la Première Guerre mondiale lorsque les réserves allemandes de composés azotés, qui étaient utilisés pour les explosifs, ont été épuisées en 1914.

Réponse

K_C = 0,105 ; K_P = 2,61 × 10-5

Calcul de la (des) concentration(s) à l’équilibre

Dans ce type de problèmes d’équilibre, si nous connaissons la constante d’équilibre d’une réaction et les concentrations à l’équilibre de tous les réactifs et produits sauf un, nous pouvons calculer la concentration manquante.

Exemple 4.3.4 – Calcul d’une concentration manquante à l’équilibre

Les oxydes d’azote sont des polluants atmosphériques produits par la réaction de l’azote et de l’oxygène à haute température. À 2000°C, la valeur de la constante d’équilibre K_C de la réaction, N₂ (g) + O₂ (g) ⇌ 2 NO (g), est de 4,1 × 10^-4. Calculer la concentration d’équilibre de NO (g) dans l’air à une pression de 1,00 atm et à 2000°C. Les concentrations d’équilibre de N₂ et de O₂ à cette pression et à cette température sont respectivement de 0,036 M et 0,0089 M.

Solution

On nous donne toutes les concentrations d’équilibre sauf celle du NO. Ainsi, nous pouvons résoudre la concentration d’équilibre manquante en réorganisant l’équation pour la constante d’équilibre.

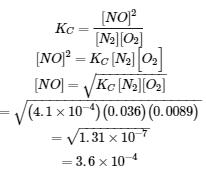
Ainsi, [NO] est de 3,6 × 10^-4 mol/L à l’équilibre dans ces conditions.

Nous pouvons vérifier notre réponse en substituant toutes les concentrations d’équilibre dans l’expression au quotient de réaction, Q_C, pour voir s’il est égal à la constante d’équilibre, et ainsi confirmer que le système est bien à l’équilibre.

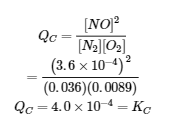
La réponse est logique ; notre valeur calculée donne la constante d’équilibre au sein de l’erreur associée aux chiffres significatifs du problème.

Vérifiez votre apprentissage 4.3.4 – Calcul d’une concentration manquante à l’équilibre

La constante d’équilibre pour la réaction de l’azote et de l’hydrogène pour produire de l’ammoniac à une certaine température est de 6,00 × 10^-2. Calculer la concentration d’équilibre de l’ammoniac si les concentrations d’équilibre de l’azote et de l’hydrogène sont respectivement de 4,26 M et 2,09 M.

Réponse

1,53 mol/L

         Dans un autre scénario, si nous connaissons la constante d’équilibre d’une réaction et un ensemble de concentrations de réactifs et de produits qui ne sont pas à l’équilibre, nous pouvons calculer les changements de concentrations au fur et à mesure que le système s’équilibre, ainsi que les nouvelles concentrations à l’équilibre. La procédure typique peut être résumée en quatre étapes.

1. Déterminer la direction que prend la réaction pour parvenir à l’équilibre.

         a. Rédigez une équation chimique équilibrée pour la réaction.

         b. Si la direction dans laquelle la réaction doit se dérouler pour atteindre                     

l’équilibre n’est pas évidente, calculer Q à partir des valeurs initiales et le                     

comparer à K pour déterminer la direction du changement.

2. Déterminez les changements relatifs nécessaires pour atteindre l’équilibre, puis écrivez les concentrations d’équilibre en fonction de ces changements.

         a. Définir les modifications des concentrations initiales qui sont nécessaires                 

pour que la réaction atteigne l’équilibre. En général, nous représentons le plus           

petit changement avec le symbole x et exprimons les autres changements en             

termes de plus petit changement.

         b. Définir les concentrations d’équilibre manquantes en fonction des                             

concentrations initiales et des changements de concentration déterminés au               

point (a).

3. Résoudre le changement et les concentrations d’équilibre.

         a. Substituer les concentrations d’équilibre dans l’expression pour la constante           

d’équilibre, résoudre x, et vérifier toutes les hypothèses utilisées pour trouver             

x.

         b. Calculer les concentrations à l’équilibre.

4. Vérifiez l’arithmétique.

5. Vérifiez les concentrations d’équilibre calculées en les substituant dans l’expression d’équilibre et en déterminant si elles donnent la constante d’équilibre.

Parfois, une étape particulière peut différer d’un problème à l’autre – elle peut être plus complexe pour certains problèmes et moins complexe pour d’autres. Cependant, tout calcul des concentrations d’équilibre à partir d’un ensemble de concentrations initiales comportera ces étapes.

Pour résoudre les problèmes d’équilibre qui impliquent des changements de concentration, il est à nouveau très pratique de mettre en place une table de ICE.

Exemple 4.3.5 – Calcul des variations de concentration en réaction à l’équilibre

Dans certaines conditions, la constante d’équilibre K_C pour la décomposition de PCl₅ (g) en PCl₃ (g) et Cl₂ (g) est de 0,0211. Quelles sont les concentrations d’équilibre de PCl₅, PCl₃ et Cl₂ si la concentration initiale de PCl₅ était de 1,00 M ?

Solution

Utilisez le processus par étapes décrit plus haut.

1. Déterminer la direction de la réaction.

L’équation équilibrée pour la décomposition de la PCl₅ est

PCl₅ (g) ⇌ PCl₃ (g) + Cl₂ (g)

Comme nous n’avons pas de produits au départ, Q = 0 et la réaction doit se faire vers la droite (vers les produits).

2. Déterminez les changements relatifs nécessaires pour atteindre l’équilibre, puis écrivez les concentrations d’équilibre en fonction de ces changements.

Représentons l’augmentation de la concentration de PCl₃ par le symbole x. Les autres changements peuvent être écrits en termes de x en considérant les coefficients de l’équation chimique.

PCl₅ (g) ⇌ PCl₃ (g) + Cl₂ (g)

– x           + x             + x

Les changements de concentration et les expressions pour les concentrations d’équilibre sont :

PCl₅   ⇌   PCl₃ + Cl₂

3. Rechercher les concentrations de changement et d’équilibre.

La substitution des concentrations d’équilibre dans l’équation de la constante d’équilibre donne

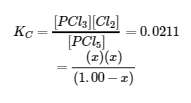
Cette équation ne contient qu’une seule variable, x, la variation de la concentration. Nous pouvons écrire l’équation comme une équation quadratique et résoudre x en utilisant la formule quadratique.

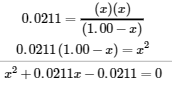
L’annexe C nous montre une équation de la forme ax2 + bx + c = 0 qui peut être réarrangée pour résoudre x :

Dans ce cas, a = 1, b = 0,0211, et c = -0,0211. En substituant les valeurs appropriées à a, b et c, on obtient le rendement :

Dans ce cas, la deuxième solution (-0,156) est physiquement impossible parce que nous savons que la variation doit être un nombre positif (sinon nous nous retrouverions avec des valeurs négatives pour les concentrations des produits). Ainsi, x = 0,135 M.

Les concentrations d’équilibre sont les suivantes

[PCl₅] = 1,00 – 0,135 = 0,87 M

[PCl₃] = x = 0,135 M

[Cl₂] = x = 0,135 M

4. Vérifiez l’arithmétique.

La substitution dans l’expression de Kc (pour vérifier le calcul) donne

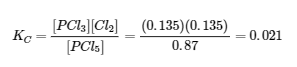
La constante d’équilibre calculée à partir des concentrations d’équilibre est égale à la valeur de Kc donnée dans le problème (lorsqu’elle est arrondie au nombre approprié de chiffres significatifs). Ainsi, les concentrations d’équilibre calculées sont confirmées.

Vérifiez votre apprentissage 4.3.5 – Calcul des variations de concentration en réaction à l’équilibre

L’acide acétique, CH₃CO₂H, réagit avec l’éthanol, C₂H₅OH, pour former de l’eau et de l’acétate d’éthyle, CH₃CO₂C₂H₅.

CH₃CO₂H + C₂H₅OH ⇌ CH₃CO₂C₂H₅ + H₂O

La constante d’équilibre de cette réaction à une certaine température, en utilisant le dioxane comme solvant, est de 4,0. Quelles sont les concentrations d’équilibre lorsque 0,15 mol de CH₃CO₂H, 0,15 mol de C₂H₅OH, 0,40 mol de CH₃CO₂C₂H₅ et 0,40 mol de H₂O sont mélangés dans suffisamment de solvant à base de dioxane pour obtenir 1,0 L de solution ?

Réponse

[CH₃CO₂H] = 0,36 M, [C₂H₅OH] = 0,36 M, [CH₃CO₂C₂H₅] = 0,17 M, [H₂O] = 0,17 M

Vérifiez votre apprentissage 4.3.6 – Calcul des variations de concentration en réaction à l’équilibre

Un flacon de 1,00 L est rempli de 1,00 mole de H₂ et de 2,00 moles de I₂. La valeur de la constante d’équilibre KC pour la réaction de l’hydrogène et de l’iode réagissant pour former de l’iodure d’hydrogène est de 50,5 dans les conditions données. Quelles sont les concentrations d’équilibre de H₂, I2 et HI en mol/L ?

H₂ (g) + I₂ (g) ⇌ 2 HI (g)

Réponse

H₂ = 0,06 M, I₂ = 1,06 M, HI = 1,88 M

Considérons maintenant un autre exemple où nous pouvons utiliser une méthode de raccourci de racine carrée pour faciliter la résolution des problèmes. Si nous constatons que le terme fractionnaire composé de réactifs (dénominateur) et de produits (numérateur) a des carrés parfaits, nous pouvons prendre la racine carrée des deux côtés lors de la résolution pour x.

Exemple 4.3.6 – La concentration change en réaction à l’équilibre – Racine carrée

La réaction de déplacement eau-gaz est importante dans plusieurs processus chimiques, comme la production de H₂ pour les piles à combustible. Cette réaction peut s’écrire comme suit :

H₂ (g) + CO₂ (g)  ⇌  H₂O _(g) + CO (g)

K_C = 0,106 à 700 K. Si on laisse un mélange de gaz qui contient initialement 0,0150 M en H₂ et 0,0150 M en CO₂ s’équilibrer à 700 K, quelles sont les concentrations finales de toutes les substances présentes ?

Solution

Les concentrations initiales des réactifs sont [H₂]_i = [CO₂]_i = 0,0150 M. Comme précédemment, nous nous concentrerons sur la variation des concentrations des différentes substances entre l’état initial et l’état final. Si nous définissons le changement de la concentration de H₂O comme x, alors Δ [H₂O] = +x. Nous pouvons utiliser la stœchiométrie de la réaction pour exprimer les changements des concentrations des autres substances en termes de x. Par exemple, 1 mol de CO est produite pour 1 mol de H₂O, donc le changement de la concentration de CO peut être exprimé comme Δ [CO] = +x. De même, pour chaque mole de H₂O produite, 1 mole d _H2 et 1 mole de CO₂ sont consommées, de sorte que la variation de la concentration des réactifs est exprimée par Δ [H₂] = Δ [CO_{2] =} -x. Nous saisissons les valeurs dans le tableau suivant et calculons les concentrations finales.

Nous pouvons maintenant utiliser l’équation d’équilibre et le K donné pour résoudre x :

Nous pourrions résoudre cette équation avec la formule quadratique, mais il est beaucoup plus facile de résoudre pour x en reconnaissant que le côté gauche de l’équation est un carré parfait, c’est-à-dire,

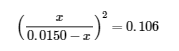
En prenant la racine carrée des deux côtés de cette équation, on obtient

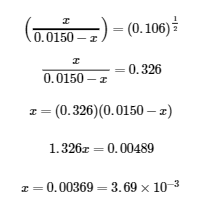
Les concentrations finales de toutes les espèces dans le mélange réactionnel sont les suivantes :

Nous pouvons vérifier notre travail en réinscrivant les valeurs calculées dans l’expression de la constante d’équilibre :

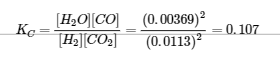
Pour deux chiffres significatifs, cette K_C est la même que la valeur donnée dans le problème, donc notre réponse est confirmée.

Vérifiez votre apprentissage 4.3.7 – La concentration change en réaction à l’équilibre – Racine carrée

L’hydrogène gazeux réagit avec la vapeur d’iode pour donner de l’iodure d’hydrogène selon l’équation chimique suivante :

H₂ (g) + I₂ (g) ⇌ 2 HI (g)

K_C = 54,0 à 425°C. Si 0,172 M H₂ et I₂ sont injectés dans un réacteur et maintenus à 425°C jusqu’à ce que le système s’équilibre, quelle est la concentration finale de chaque substance dans le mélange réactionnel ?

Réponse

[HI]_f = 0,270 M ; [H₂]_f = [I₂]_{f =} 0,037 M

Il est parfois possible d’utiliser l’intuition chimique pour trouver des solutions à des problèmes d’équilibre sans pour autant résoudre une équation quadratique (ou plus compliquée). Cependant, il est d’abord utile de vérifier que l’équilibre peut être obtenu à partir de deux extrêmes : tous (ou principalement) les réactifs et tous (ou principalement) les produits.

Considérons l’ionisation de 0,150 M HA, un acide faible.

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

La façon la plus évidente de déterminer les concentrations d’équilibre serait de commencer dans un système ne contenant que des réactifs. C’est ce qu’on pourrait appeler le point de départ “tous les réactifs”. En utilisant x pour la quantité d’acide ionisé à l’équilibre, on obtient le tableau et la solution de la ICE.

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

La mise en place et la résolution de l’équation quadratique donne

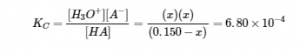
En utilisant la racine positive (physique), les concentrations d’équilibre sont

[HA] = 0,150 – x = 0,140 M

[H₃O⁺] = [A^–] = x = 0,00977 M

Une façon moins évidente de résoudre le problème serait de supposer que tout l’HA ionise d’abord, et que le système s’équilibre. C’est ce que l’on pourrait appeler le point de départ “tous les produits”. En supposant que tout l’HA ionisé donne

[HA] = 0,150 – 0,150 = 0 M

[H₃O⁺] = 0 + 0,150 = 0,150 M

[A^–] = 0 + 0,150 = 0,150 M

En utilisant ces données comme concentrations initiales et “y” pour représenter la concentration d’HA à l’équilibre, voici le tableau ICE pour ce point de départ.

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

La mise en place et la résolution de l’équation quadratique donne

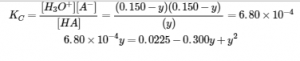
Conservez quelques chiffres significatifs supplémentaires pour minimiser les problèmes d’arrondissement.

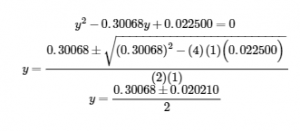
En arrondissant chaque solution à trois chiffres significatifs, on obtient

y = 0,160 M ou y = 0,140 M

L’utilisation de la racine physiquement significative (0,140 M) donne les concentrations d’équilibre comme

[HA] = y = 0,140 M

[H₃O⁺] = 0,150 – y = 0,010 M

[A-] = 0,150 – y = 0,010 M

Ainsi, les deux approches donnent les mêmes résultats (à trois décimales de précis), et montrent que les deux points de départ conduisent aux mêmes conditions d’équilibre (figure 4.3.3). Le point de départ “tous les réactifs” a donné lieu à une variation relativement faible (x) parce que le système était proche de l’équilibre, tandis que le point de départ “tous les produits” a donné lieu à une variation relativement importante (y) qui était proche de la taille des concentrations initiales. Remarquez que le graphique de la partie (a) de la figure 4.3.3 présente peu de changement de concentration ; on peut donc dire qu’un système qui commence “près” de l’équilibre n’aura besoin que d’un “petit” changement des conditions (x) pour atteindre l’équilibre.

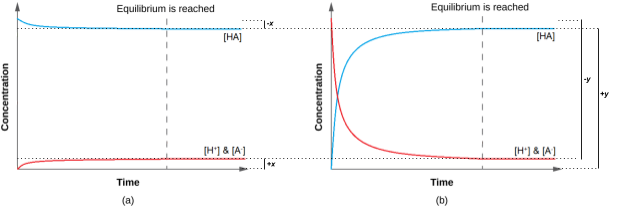
Figure 4.3.3. Quel que soit le point de départ, que ce soit avec 100 % de réactifs en (a) ou 100 % de produits en (b), on se retrouve quand même au même point d’équilibre. (a) La variation des concentrations de réactifs et de produits est représentée par la réaction HA (aq) ⇌ H⁺ (aq) + A^– (aq) approche de l’équilibre, lorsque l’on part d’un point de départ “tous réactifs”. (b) Le changement dans les concentrations des réactifs et des produits est représenté par la réaction HA (aq) ⇌ H⁺ (aq) + A^– (aq) approche de l’équilibre, en partant d’un point de départ “tous produits”.

Rappelons qu’une petite valeur de K signifie que très peu de réactifs forment des produits et qu’un grand K signifie que la plupart des réactifs forment des produits. Si le système peut être agencé de manière à ce qu’il commence à être “proche” de l’équilibre, alors si la variation (x) est faible par rapport à une quelconque concentration initiale, elle peut être négligée. Les deux exemples suivants le démontrent.

Exemple 4.3.7 – Solution approximative commençant près de l’équilibre

Quelles sont les concentrations à l’équilibre d’une solution de HCN à 0,15 M ?

HCN (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CN^– (aq)      K = 4,9 x 10^-10

Solution

L’utilisation de “x” pour représenter la concentration de chaque produit à l’équilibre donne ce tableau ICE.

HCN (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CN^– (aq)

La solution exacte peut être obtenue en utilisant la formule quadratique avec

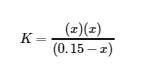
résoudre

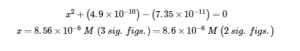
Ainsi, [H₃O⁺] = [CN^–] = x = 8,6 × 10^-6 M et [HCN] = 0,15 – x = 0,15 M.

Dans ce cas, l’intuition chimique peut fournir une solution plus simple. À partir de la constante d’équilibre et des conditions initiales, x doit être petit par rapport à 0,15 M. Plus formellement, si x ≪ 0,15, alors 0,15 – x ≈ 0,15 (la figure 4.3.4 le démontre visuellement).

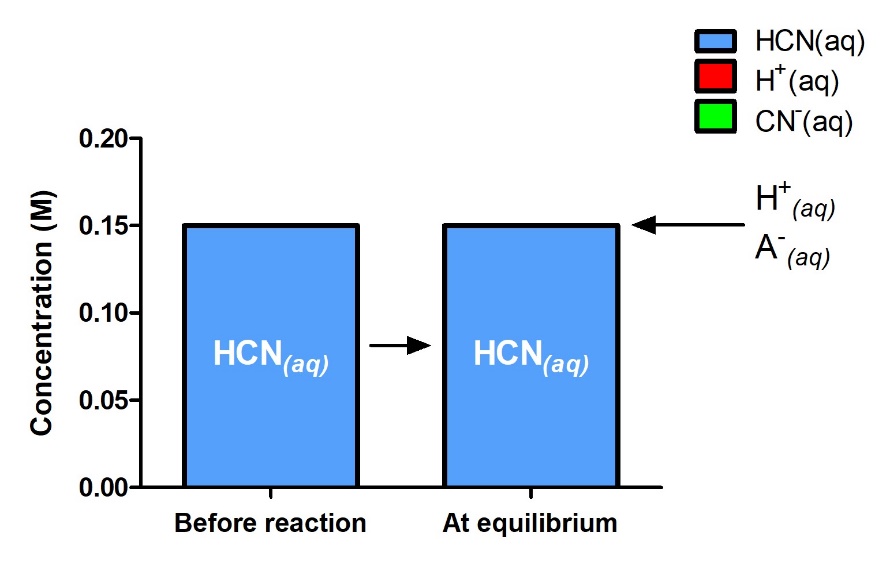
Figure 4.3.4. Les concentrations du réactif et des produits sont indiquées au départ et à l’équilibre pour la réaction suivante : HCN (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CN^– (aq). La réaction commence avec seulement HCN(aq), mais même à l’équilibre, on peut dire que les quantités relatives de H⁺ et CN^– sont si faibles qu’elles sont négligeables – il n’y a pratiquement encore que le réactif qui démontre la valeur K extrêmement faible de la réaction et confirme la validité de l’hypothèse selon laquelle 0,15 – x ≈ 0,15.

Si cette hypothèse est vraie, alors elle simplifie l’obtention de x

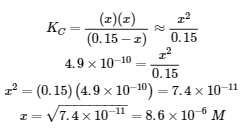
Dans cet exemple, la résolution de l’équation exacte (quadratique) et l’utilisation d’approximations ont donné le même résultat à deux chiffres significatifs. Bien que la plupart du temps l’approximation soit un peu différente de la solution exacte, tant que l’erreur est inférieure à 5%, la solution approximative est considérée comme valable. Dans ce problème, les 5% s’appliquent à (0,15 – x) ≈ 0,15 M, donc si

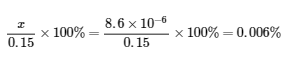
est inférieure à 5 %, comme c’est le cas ici, l’hypothèse est valable. La solution approximative est donc une solution valable.

Vérifiez votre apprentissage 4.3.8 – Solution approximative commençant près de l’équilibre

Quelles sont les concentrations d’équilibre dans une solution de NH3 à 0,25 M ?

NH₃ (aq) + H₂O (l) ⇌ NH₄⁺ (aq) + OH^– (aq)      K = 1,8 x 10^-5

Supposez que x est bien inférieur à 0,25 M et calculez l’erreur dans votre hypothèse.

Réponse

[OH-] = [NH₄+] = 0,0021 M ; [NH₃] = 0,25 M, erreur = 0,84%.

Le deuxième exemple exige que l’information originale soit un peu traitée, mais elle peut encore être résolue en utilisant une petite approximation x.

Exemple 4.3.8 – Solution approximative après modification de la concentration de départ

Les ions de cuivre_(II) forment un ion complexe en présence d’ammoniac

Si l’on ajoute 0,010 mol Cu²⁺ à 1,00 L d’une solution de 1,00 M NH₃, quelles sont les concentrations lorsque le système atteint l’équilibre ?

Solution

La concentration initiale de cuivre(II) est de 0,010 M. La constante d’équilibre est très grande, il serait donc préférable de commencer avec le plus de produit possible car “tous les produits” est beaucoup plus proche de l’équilibre que “tous les réactifs” (figure 4.3.5). Par conséquent, pour simplifier nos calculs, supposons que la réaction se termine à 100 %. Notez que Cu2+ est le réactif limitant ; si la totalité des 0,010 M réagit pour former un produit, les concentrations seraient

être

[Cu2+]= 0,010 – 0,010 = 0 M

[Cu(NH₃)₄²⁺] = 0,010 M

[NH₃] = 1,00 – 4 x 0,010 = 0,96 M

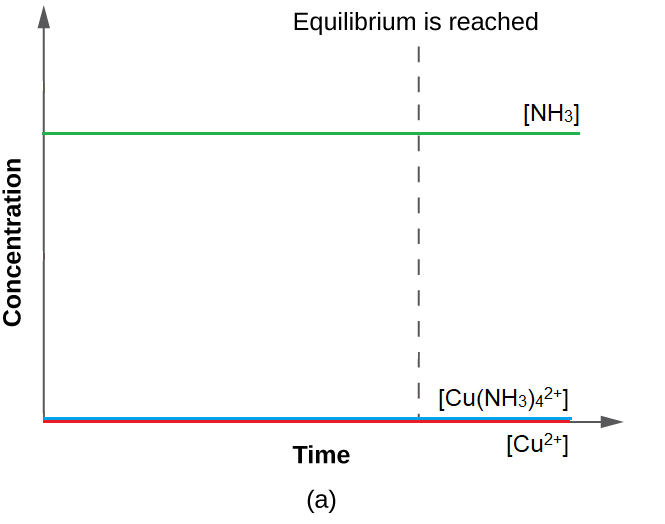
Figure 4.3.5. La valeur K est très importante pour la réaction d’équilibre Cu²⁺(aq) + 4 NH₃(aq) ⇌ Cu(NH₃)₄²⁺(aq), les produits sont donc très fortement favorisés. La modification de la concentration des produits et des réactifs est presque minime car, dans l’état actuel des choses, la concentration relative de toutes les espèces correspond déjà presque aux quantités relatives à l’équilibre, où le produit est proche de sa concentration maximale possible.

L’utilisation de ces valeurs “décalées” comme concentrations initiales, avec x comme concentration d’ions cuivre(II) libres à l’équilibre, donne ce tableau de la ICE.

Cu²⁺ (aq) + 4 NH₃ (aq)  ⇌  Cu(NH₃)₄²⁺ (aq)

Comme nous commençons à nous rapprocher de l’équilibre, x doit être petit pour que

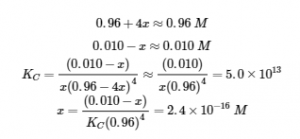
Choisissez la plus petite concentration pour la règle des 5 % – en divisant une valeur par la plus petite valeur possible, on obtient l’erreur la plus grande possible pour mettre réellement la règle des 5 % à l’épreuve.

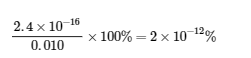
Ce chiffre est bien inférieur à 5 %, les hypothèses sont donc valables. Les concentrations à l’équilibre sont

[Cu²⁺] = x = 2,4 x 10^-16 M

[NH₃] = 0,96 – 4x = 0,96 M

[Cu(NH₃)₄²⁺] = 0,010 – x = 0,010 M

Si nous soustrayons x de 0,010 M, par exemple, nous obtenons 0,00999999… M qui, en comptant les chiffres significatifs, s’arrondit de toute façon à 0,010 M.

Dans l’ensemble, nous avons commencé avec une concentration beaucoup plus élevée de réactif par rapport au produit – notez que nous utilisons du Cu²⁺, donc au départ, nous avons la concentration de produits la plus élevée possible. Mais comme K a une valeur très grande, la modification de la concentration est maintenue minimale puisque ce mélange réactionnel correspond presque pratiquement à ce que l’on attend à l’équilibre.

En partant de la quantité maximale de produit, ce système était proche de l’équilibre et la variation (x) était très faible – cette très faible variation était notamment due à l’absence totale de Cu²⁺ au départ (nous en parlons dans le contexte du principe du Châtelier dans la section suivante). Avec seulement un petit changement nécessaire pour atteindre l’équilibre, l’équation pour x a été grandement simplifiée et a donné un résultat valide bien en dessous du maximum d’erreur de 5%.

Vérifiez votre apprentissage 4.3.9 – Solution approximative après modification de la concentration de départ

Quelles sont les concentrations d’équilibre lorsque 0,25 mol de Ni²⁺ est ajouté à 1,00 L de solution NH3 à 2,00 M ?

Ni²⁺ (aq) + 6 NH₃ (aq) ⇌ Ni(NH₃)₆²⁺ (aq)      K_C = 5,5 x 10⁸

Avec une constante d’équilibre aussi élevée, il faut d’abord former autant de produit que possible, puis supposer qu’il ne reste qu’une petite quantité (x) du produit. Calculez l’erreur de votre hypothèse.

Réponse

[Ni(NH₃)₆²⁺] = 0,25 M, [NH₃] = 0,50 M, [Ni²⁺] = 2,9 × 10^-8 M, erreur = 1,2 × 10^-5 %.

Questions

★ Questions

1. Dans la réaction d’équilibre A + B ⇌ C, qu’arrive-t-il à K si les concentrations des réactifs sont doublées ? triplées ? Peut-on en dire autant de la réaction d’équilibre A ⇌ B + C ?

2. Le tableau suivant indique les valeurs de l’équilibre P_(O2) à trois températures pour la réaction Ag₂O (s) ⇌ 2 Ag (s) + 1/2 O₂ (g) pour laquelle ΔH° = 31 kJ/mol. Ces données sont-elles cohérentes avec ce que vous attendez ? Pourquoi ou pourquoi pas ?

3. Étant donné le système d’équilibre N₂O₄ (g) ⇌ 2 NO₂ (g), qu’arrive-t-il au K_P si la pression initiale du N₂O₄ est doublée ? Si K_P est de 1,7 × 10^-1 à 2300°C, et que le système contient initialement 100% de N2O4 à une pression de 2,6 × 10² bar, quelle est la pression d’équilibre de chaque composant ?

4. À 430 °C, 4,20 moles de HI dans une cuve de réaction de 9,60 L atteignent l’équilibre selon l’équation suivante : H₂ (g) + I₂ (g) ⇌ 2 HI (g). À l’équilibre, [H₂] = 0,047 M et [HI] = 0,345 M. Quels sont le K et le K_P pour cette réaction ?

5. Le méthanol, un liquide utilisé comme additif pour les carburants automobiles, est produit commercialement à partir de monoxyde de carbone et d’hydrogène à 300°C selon la réaction suivante : CO (g) + 2 H₂ (g) ⇌ CH₃OH (g) et K_P = 1,3 × 10^-4. Si l’on mélange 56,0 g de CO avec un excès d’hydrogène dans un ballon de 250 ml à cette température, et que la pression de l’hydrogène est maintenue en permanence à 100 bars, quel serait le rendement maximal en pourcentage de méthanol ? Quelle pression d’hydrogène serait nécessaire pour obtenir un rendement minimal de 95 % de méthanol dans ces conditions ?

★★ Questions

6. En partant de A pur, si la pression d’équilibre totale est de 0,969 atm pour la réaction A (s) ⇌ 2 B (g) + C (g), qu’est-ce que le K_P (indice : il faut utiliser l’unité “bar” lorsqu’on travaille avec le KP) ?

7. La décomposition du carbamate d’ammonium en NH₃ et CO₂ à 40°C s’écrit NH₄CO₂NH₂ (s) ⇌ 2 NH₃ (g) + CO₂ Si la pression partielle de NH₃ à l’équilibre est de 0,242 atm, quelle est la pression partielle d’équilibre (en atm) du CO₂ ? Quelle est la pression gazeuse totale du système (en atm) ? Qu’est-ce que le K_P (conseil : il faut utiliser l’unité “bar” lorsqu’on travaille avec le Kp) ?

8. À 375 K, le K_P pour la réaction SO₂Cl₂ (g) ⇌ SO₂ (g) + Cl₂ (g) est de 2,4, avec des pressions exprimées en atmosphères. À 303 K, le KP est de 2,9 × 10^-2.

         a. Quelle est la valeur de K pour la réaction à chaque température ?

         b. Si un échantillon à 375 K contient 0,100 M Cl₂ et 0,200 M SO₂ à l’équilibre,               quelle est la concentration de SO₂Cl₂ ?

         c. Si l’échantillon donné dans la partie b est refroidi à 303 K, quelle est la                       pression à l’intérieur de l’ampoule (en atm) ?

9. Les données expérimentales sur le système Br2 (l) ⇌ Br2 (aq) sont données dans le tableau suivant. Graphique [Br2] en fonction des moles de Br2 (l) présentes ; puis écrire l’expression de la constante d’équilibre et déterminer K.

10. Les données accumulées pour la réaction n-butane (g) ⇌ isobutane (g) à l’équilibre sont présentées dans le tableau suivant. Quelle est la constante d’équilibre pour cette conversion ? Si on laisse 1 mol de n-butane s’équilibrer dans les mêmes conditions de réaction, quel est le nombre final de moles de n-butane et d’isobutane ?

11. Le carbamate d’ammonium solide (NH₄CO₂NH₂) se dissocie complètement en ammoniac et en dioxyde de carbone lorsqu’il se vaporise :

NH₄CO₂NH₂ (s) ⇌ 2 NH₃ (g) + CO₂ (g)

A 25°C, la pression totale des gaz en équilibre avec le solide est de 0,116 atm. Quelle est la pression partielle à l’équilibre de chaque gaz (en atm) ? Qu’est-ce que le Kp (indice : il faut utiliser l’unité “bar” lorsqu’on travaille avec le K_P) ? Si la concentration de CO₂ est doublée et s’équilibre ensuite à sa pression partielle d’équilibre initiale +x atm, quelle modification de la concentration de NH3 est nécessaire pour que le système rétablisse l’équilibre ?

12. La constante d’équilibre pour la réaction COCl₂ (g) ⇌ CO (g) + Cl₂ (g) est K_P = 2,2 × 10^-10 à 100°C. Si la concentration initiale de COCl₂ est de 3,05 × 10^-3 M, quelle est la pression partielle de chaque gaz à l’équilibre à 100°C (en bar) ? Quelle hypothèse peut-on faire pour simplifier vos calculs ?

13. La dilution aqueuse de IO₄^– entraîne la réaction suivante :

IO^4- (aq) + 2 H₂O (l) ⇌ H₄IO^6- (aq)

et K = 3,5 × 10^-2. Si vous commencez avec 50 ml d’une solution de IO^4- 0,896 M diluée à 250 ml avec de l’eau, combien de moles de H₄IO^6- se forment à l’équilibre ?

★★★ Questions

14. L’iode et le brome réagissent pour former l’IBr, qui se sublime ensuite. À 184,4 °C, la réaction globale se déroule selon l’équation suivante :

I₂ (g) + Br₂ (g) ⇌ 2 IBr (g)

K_P = 1,2 × 10² (Indice : on suppose que l’on a utilisé “bar” comme unité lors du calcul de K_P). Si vous commencez la réaction avec 7,4 g de vapeur de I₂ et 6,3 g de vapeur de Br2 dans un récipient de 1,00 L, quelle est la concentration d’IBr (g) à l’équilibre (gmol^-1) ? Quelle est la pression partielle de chaque gaz à l’équilibre (en bar) ? Quelle est la pression totale du système (en bar) ?

15. Pour la réaction

C (s) + 12 N₂ (g) + 5/2 H₂ (g) ⇌ CH₃NH₂ (g)

K = 1.8 × 10⁻⁶. Si vous commencez la réaction avec 1,0 mole de N₂, 2,0 moles de H₂ et suffisamment de C(s) dans un récipient de 2,00 L, quelles sont les concentrations de N₂ et de CH3NH2 à l’équilibre (gmol-1) ? Qu’arrive-t-il à K si la concentration de H₂ est doublée ?

Réponses

1. La valeur K est maintenant élevée au niveau du facteur respecté. Lorsqu’il est doublé, K est maintenant K₂ et lorsqu’il est triplé, K est K₃
2. Ces résultats ne sont pas attendus, car en cas d’augmentation de la température, une augmentation de la pression devrait se produire. ∆H० est une valeur positive dans ce cas (31 kJ/mol) indiquant qu’il s’agit d’une réaction endothermique. Cela dit, avec une augmentation de la température, la réaction se déplacera vers l’avant, ce qui signifie que davantage de produit sera produit. Si plus de produit est produit, plus d’oxygène gazeux est présent, ce qui augmente sa pression.
3. Kp resterait le même, P_N2O2 = 2,3 x 10² bar, P_NO2 = 6,6 bar
4. K = 53,88 ; Kp = 53,88
5. 215 bar MeOH ; 383 bar H₂
6. Kp = 0,140
7. Pression partielle du CO₂ = 0,121 atm ; pression totale du gaz du système = 0,363 atm ; Kp = 7,37 x 10-3
8. (a) K = 7,8 x 10-2 à 375K, K = 1,2 x 10-3 à 303K ; (b) 0,256 M ; (c) 14,13 atm
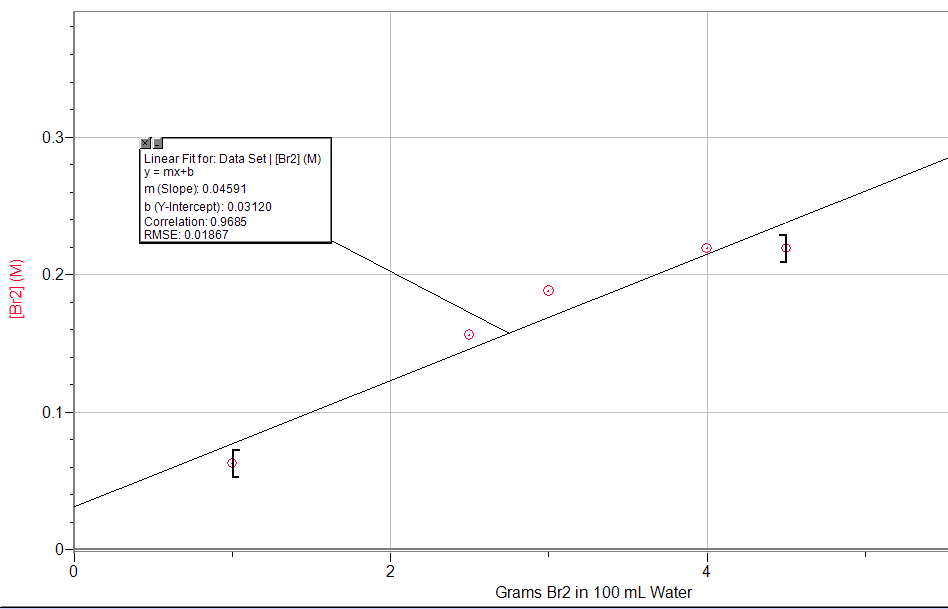9. K = 0,046 (basé sur la pente de la régression linéaire)
10. K = 2,5 ; les moles finales seront de 0,3 mole de n-butane et de 0,7 mole d’isobutane.
11. P_{NH3 =} 0,0773 atm, P_CO2 = 0,0387 atm ; K_p = 2,411 x 10^-4 ; la concentration de NH3 diminuera afin que l’équilibre se rétablisse.
12. PCOCl₂ = 0,042 bar, PCO = 4,59 x 10^-6 bar, P_Cl2 = 4,59 x 10^-6 bar ; On suppose que le volume total est de 1L.
13. H₄IO^6- = 9,09 x 10^-3 mol
14. P_I2 = 7,7 bar, P_Br2 = 47 bar, P_{IBr =} 2,1 x10² bar = 0,054 M, P_{T =} 2,6 x 10² bar
15. [N₂] ≈ 0,99 M, [H₂] ≈ 2 M, [CH₃NH₂] = 1,02 x 10^-5 M ; si le [H₂] double, K reste inchangé (seule la température peut modifier une valeur K)