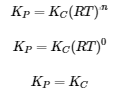4.2 – La constante d’équilibre et le quotient de réaction

Dans la section précédente, nous avons commencé à dériver une constante pour les équilibres chimiques basée sur la cinétique des réactions en amont et en aval. Nous avons établi que la composition du mélange d’équilibre est déterminée par les amplitudes des constantes de vitesse des réactions directe et inverse, ou plus précisément que la constante d’équilibre est égale à la constante de vitesse de la réaction directe divisée par la constante de vitesse de la réaction inverse. Nous allons ici développer une expression de la constante d’équilibre pour K applicable à toute réaction d’équilibre et examiner comment nous pouvons également prédire la direction du changement net étant donné une quantité donnée de réactifs et de produits.

La constante d’équilibre (K)

En 1864, les chimistes norvégiens Cato Guldberg (1836-1902) et Peter Waage (1833-1900) ont soigneusement mesuré la composition de nombreux systèmes réactionnels à l’équilibre. Ils ont découvert que pour toute réaction réversible de la forme générale

m A + n B ⇌ x C + y D

où A et B sont des réactifs, C et D sont des produits, et m, n, x et y sont les coefficients stœchiométriques dans l’équation chimique équilibrée pour la réaction, le rapport du produit des quantités d’équilibre des produits (portées à leurs coefficients dans l’équation chimique équilibrée) au produit des concentrations d’équilibre des réactifs (portées à leurs coefficients dans l’équation chimique équilibrée) est toujours une constante dans un ensemble donné de conditions. Cette relation a finalement été résumée comme suit :

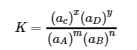
4.2.1

où K est la constante d'équilibre de la réaction, équivalente à la valeur définie au point 4.1, et aX représente l’activité de chaque espèce participant à l’équilibre. L’équation d’équilibre chimique représentée avec les réactifs A & B et les produits C & D est appelée l’équation d’équilibre, et le côté droit de l’équation mathématique ci-dessus est appelé l’expression de la constante d’équilibre. La relation indiquée dans l’expression pour K est vraie pour toute paire de réactions opposées, quel que soit le mécanisme de la réaction ou le nombre d’étapes du mécanisme.

Un fait important à noter est que les constantes d’équilibre sont sans dimensions (elles n’ont pas d’unité) mais la température à laquelle cette valeur est valable doit toujours être indiquée (puisque K dépend de la température). Ceci est dû au calcul des valeurs de K en utilisant les activités des réactifs et des produits dans le système d’équilibre. L’activité d’une substance est une mesure de sa concentration effective dans des conditions spécifiées. Bien qu’une discussion détaillée de cette quantité importante dépasse le cadre de ce texte d’introduction, il est nécessaire d’être conscient de quelques aspects importants :

• Les activités sont des quantités sans dimension (sans unité) et sont essentiellement des quantités “ajustées” de réactifs et de produits.
• Pour des solutions relativement diluées, l’activité d’un soluté et sa concentration molaire sont à peu près égales (c’est-à-dire pour un soluté X, aX ≈ [X] en mol/L ou M). Notez que cette approximation n’est pas valable pour les solutés très concentrés.
• Pour les gaz, l’activité d’une substance est égale à sa pression partielle (c’est-à-dire aX = PX en bar)
• Les activités des phases pures condensées (solides et liquides) sont égales à 1 (c’est-à-dire aX = 1), c’est pourquoi leurs activités n’apparaissent pas dans l’expression pour K

Pour en savoir plus sur les activités, cliquez ici.

Nous classons les équilibres en deux catégories : homogènes et hétérogènes. Un équilibre homogène est un équilibre dans lequel tous les réactifs et produits sont présents dans une seule solution (par définition, un mélange homogène). Dans ce chapitre, nous nous concentrerons sur les deux types d’équilibres homogènes les plus courants : ceux qui se produisent dans des solutions en phase liquide et ceux qui impliquent exclusivement des espèces gazeuses. Un équilibre hétérogène est un système dans lequel les réactifs et les produits se trouvent en deux ou plusieurs phases. Les phases peuvent être toute combinaison de phases solides, liquides ou gazeuses, et de solutions. Lorsque vous traitez de ces équilibres, rappelez-vous que les solides et les liquides purs n’apparaissent pas dans les expressions de constantes d’équilibre (comme nous l’avons mentionné ci-dessus, les activités des solides purs, des liquides purs et des solvants sont 1).

Écrivez l’expression de la constante d’équilibre pour chaque réaction.

(a) N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

(b) CO (g) + ½ O₂ (g) ⇌ CO₂ (g)

(c) 2 CO₂ (g) ⇌ 2 CO (g) + O₂ (g)

(d) H₂O (l) + H₂CO₃ (aq) ⇌ H₃O⁺ (aq) + HCO₃^– (aq)

(e) Fe₃O₄ (s) + 4 H_{2 (}g) ⇌ 3 Fe (s) + 4 H₂O (g)

Solution

(a) Le seul produit est l’ammoniac, qui a un coefficient de 2. Pour les réactifs, N₂ a un coefficient de 1 et H₂ un coefficient de 3. Toutes les espèces sont des gaz, et leurs activités sont donc égales à leurs pressions partielles. L’expression de la constante d’équilibre est la suivante :

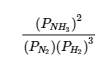
(b) Le seul produit est le dioxyde de carbone, qui a un coefficient de 1. Les réactifs sont le CO, avec un coefficient de 1, et l’O₂, avec un coefficient de ½. Comme toutes les espèces sont des gaz, l’expression de la constante d’équilibre est la suivante :

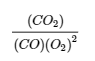
(c) Cette réaction est l’inverse de la réaction de la partie (b), tous les coefficients étant multipliés par 2 pour éliminer le coefficient fractionnaire de O₂. L’expression de la constante d’équilibre est donc l’inverse de l’expression de la partie (b), avec tous les exposants multipliés par 2 :

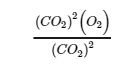
(d) Cette réaction contient un liquide pur (H₂O), son activité est égale à 1 et n’apparaît donc pas dans l’expression de la constante d’équilibre. Les trois autres espèces sont des solutés, et leurs activités peuvent être approximées à l’aide de leurs concentrations molaires :

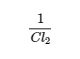
(e) Cette réaction contient deux solides purs (Fe₃O₄ et Fe), qui n’apparaissent pas dans les expressions des constantes d’équilibre. Les deux gaz apparaissent cependant dans les expressions :

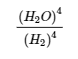
Vérifiez votre apprentissage 4.2.1 – Écrire des expressions constantes d’équilibre

Écrivez l’expression de la constante d’équilibre pour chaque réaction.

(a) N₂O (g) ⇌ N₂ (g) + 12 O₂ (g)

(b) 2 C₈H₁₈ (g) + 25 O₂ (g) ⇌ 16 CO_{2 (g}) + 18 H₂O (g)

(c) H₂ (g) + I2 (g) ⇌ 2 HI (g)

(d) CaCO₃ (s) ⇌ CaO (s) + CO₂ (g)

(e) C₆H₁₂O₆ (s) + 6 O₂ (g) ⇌ 6 CO_{2 (}g) + 6 H₂O (g)

Réponse

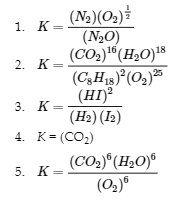
Manipulation des constantes d’équilibre

Inverser l’équation d’équilibre

Comme l’équilibre peut être approché dans les deux sens dans une réaction chimique, l’expression de la constante d’équilibre et donc l’ampleur de la constante d’équilibre dépendent de la forme sous laquelle la réaction chimique est écrite. Par exemple, si nous écrivons l’équation générique de la réaction d’équilibre à l’envers, nous obtenons ce qui suit :

c C + d D ⇌ a A + b B

Si toutes les espèces sont des solutés, alors la constante d’équilibre correspondante K’ est la suivante :

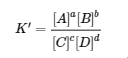
4.2.2

Cette expression est l’inverse de l’expression de la constante d’équilibre initiale, donc K’ = 1/K. C’est-à-dire que lorsque nous écrivons une réaction dans le sens inverse, l’expression de la constante d’équilibre est inversée. Voici un exemple :

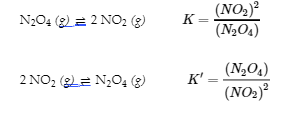
Prenons un autre exemple, la formation de l’eau : 2 H₂ (g) + O₂ (g) ⇌ 2 H₂O (g). Comme H₂ est un bon réducteur et que O₂ est un bon oxydant, cette réaction a une très grande constante d’équilibre (K = 2,4 × 10⁴⁷ à 500 K). Par conséquent, la constante d’équilibre de la réaction inverse, c’est-à-dire la décomposition de l’eau pour former O₂ et H_2, est très faible : K‘ = 1/K = 1/(2,4 × 10⁴⁷) = 4,2 × 10^-48. Comme le suggère la très petite constante d’équilibre, l’équilibre dynamique favorise toujours très fortement la formation de molécules d’eau. Ceci est lié au fait que la décomposition de l’eau en O₂ et H₂ nécessite une quantité importante d’énergie d’activation ; un concept sur lequel nous reviendrons dans notre étude de la cinétique chimique (chapitre 7).

Modification des coefficients d’espèces

L’écriture d’une équation sous des formes différentes mais chimiquement équivalentes entraîne également une différence dans l’expression et l’ampleur de la constante d’équilibre. Par exemple, en revenant à notre équation d’équilibre inverse avec une constante d’équilibre K, nous pourrions écrire l’équation pour cette réaction

2 NO₂ (g) ⇌ N₂O₄ (g)

comme

NO₂ (g) ⇌ ½ N₂O (g)

avec la constante d’équilibre K” “comme suit :

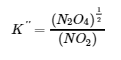
Les valeurs pour K′ et K″ sont liées comme suit :

4.2.3

En général, si tous les coefficients d’une équation chimique équilibrée sont ensuite multipliés par n, alors la nouvelle constante d’équilibre est la constante d’équilibre initiale portée à la n^ième puissance.

Combinaison des équations d’équilibre chimique

Les chimistes ont souvent besoin de connaître la constante d’équilibre d’une réaction qui n’a pas été étudiée auparavant. Dans ce cas, la réaction souhaitée peut souvent être écrite comme la somme d’autres réactions dont les constantes d’équilibre sont connues. La constante d’équilibre pour la réaction inconnue peut alors être calculée à partir des valeurs tabulées pour les autres réactions.

Pour illustrer cette procédure, considérons la réaction du N₂ avec l’O₂ pour donner du NO₂. Cette réaction est une source importante de NO₂ qui donne au smog urbain sa couleur brune typique. La réaction se produit normalement en deux étapes distinctes. Dans la première réaction (1), le N₂ réagit avec l’O₂ aux températures élevées à l’intérieur d’un moteur à combustion interne pour donner du NO. Le NO libéré réagit ensuite avec de l’O₂ supplémentaire pour donner du NO₂ (2). La constante d’équilibre pour chaque réaction à 100°C est également donnée.

N₂ (g) + O₂ (g) ⇌ 2 NO (g)       K₁ = 2,0 x 10^-25

2 NO (g) + O₂ (g) ⇌ 2 NO₂ (g)      K₂ = 6,4 x 10⁹

L’addition des réactions (1) et (2) donne la réaction globale de N₂ avec O₂ :

N₂ (g) + 2 O₂ (g) ⇌ 2 NO₂ (g)      K₃ = ?

Les expressions des constantes d’équilibre pour les réactions sont les suivantes :

Quelle est la relation entre K_1, K₂ et K₃, tous à 100°C ? L’expression pour K1 a [NO]^{2 au} numérateur, l’expression pour K2 a [NO]² au dénominateur, et [NO]² n‘apparaît pas dans l’expression pour K3. Multiplication de K1 par K2 et annulation des termes [NO]^2,

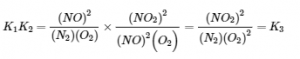
Ainsi, le produit des expressions des constantes d’équilibre pour K₁ et K₂ est le même que l’expression des constantes d’équilibre pour K₃ :

K₃ = K₁K₂ = (2.0 × 10^-25)(6.4 × 10⁹) = 1.3 × 10-¹⁵

La constante d’équilibre d’une réaction qui est la somme de deux ou plusieurs réactions est égale au produit des constantes d’équilibre des réactions individuelles. En revanche, rappelons que selon la loi de Hess (voir le chapitre précédent sur la thermochimie), ΔH pour la somme de deux ou plusieurs réactions est la somme des valeurs de ΔH pour les réactions individuelles.

Résumé

Il est important de se rappeler qu’une constante d’équilibre est toujours liée à une équation chimique spécifique, et si vous manipulez l’équation de quelque façon que ce soit, la valeur de K changera. Heureusement, les règles sont très simples :

• L’écriture de l’équation à l’envers inversera l’expression d’équilibre (c’est-à-dire K’ = 1/K)
• En multipliant les coefficients par un facteur commun n, on obtient K à la puissance correspondante de n (c’est-à-dire K’ = Kⁿ où n est un facteur commun)
• La constante d’équilibre pour une réaction qui est la somme de plusieurs équations d’équilibre chimique est le produit des constantes d’équilibre pour chacune des étapes (c’est-à-dire K’ = K₁K₂K₃…)

Exemple 4.2.2 – Manipulation des constantes d’équilibre – 1

A 745 K, K est de 0,118 pour la réaction suivante :

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

Quelle est la constante d’équilibre pour chaque réaction connexe à 745 K ?

(a) 2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g)

(b) 12 N₂ (g) + 32 H₂ (g) ⇌ NH₃ (g)

Solution

L’expression de la constante d’équilibre pour la réaction donnée de N₂ (g) avec H₂ (g) pour produire NH₃ (g) à 745 K est la suivante :

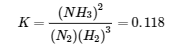
(a) Cette réaction est l’inverse de celle qui est donnée, de sorte que son expression de la constante d’équilibre est la suivante :

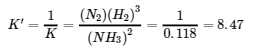
(b) Dans cette réaction, les coefficients stœchiométriques de la réaction donnée sont divisés par 2, de sorte que la constante d’équilibre est calculée comme suit :

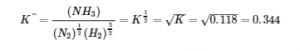
Vérifiez votre apprentissage 4.2.2 – Manipulation des constantes d’équilibre – 1

À 527 °C, la constante d’équilibre de la réaction ci-dessous est de 7,9 × 10⁴.

2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

Calculer la constante d’équilibre pour la réaction suivante à la même température :

SO₃ (g) ⇌ SO₂ (g) + ½ O₂ (g)

Répondez 

3.6 × 10^-3

Exemple 4.2.3 – Manipulation des constantes d’équilibre – 2

Les réactions suivantes se produisent à 1200°C :

CO (g) + 3 H₂ (g) ⇌ CH₄ (g) + H₂O (g)     K₁ = 9.17 × 10⁻²

CH₄ (g) + 2 H₂S (g) ⇌ CS₂ (g) + 4 H₂ (g)     K₂ = 3.3 × 10⁴

Calculer la constante d’équilibre pour la réaction suivante à la même température.

CO (g) + 2 H₂S (g) ⇌ CS₂ (g) + H₂O (g) + H₂ (g)     K₃ = ?

Solution

La clé pour résoudre ce problème est de reconnaître que la réaction 3 est la somme des réactions 1 et 2 :

CO (g) + 3 H₂ (g) ⇌ CH₄ (g) + H₂O (g)

CH₄ (g) + 2 H₂S (g) ⇌ CS₂ (g) + 4 H₂ (g)

CO (g) + 2 H₂S (g) ⇌ CS₂ (g) + H₂O (g) + H₂ (g)

Les valeurs de K₁ et K₂ sont données, il est donc facile de calculer K₃ :

K₃ = K₁K₂ = (9.17 × 10^-2)(3.3 × 10⁴) = 3.03 × 10³

Vérifiez votre apprentissage 4.2.3 – Manipulation des constantes d’équilibre – 2

Dans la première des deux étapes de la synthèse industrielle de l’acide sulfurique, le soufre élémentaire réagit avec l’oxygène pour produire du dioxyde de soufre. Dans la deuxième étape, le dioxyde de soufre réagit avec de l’oxygène supplémentaire pour former du trioxyde de soufre. La réaction de chaque étape est indiquée, ainsi que la valeur de la constante d’équilibre correspondante à 25°C. Calculer la constante d’équilibre pour l’ensemble de la réaction à cette même température.

Réponse

K₃= 1.1 × 10⁶⁶

Équilibres impliquant des gaz

Pour les réactions qui impliquent des espèces en solution, les concentrations utilisées dans les calculs d’équilibre sont des molarités, exprimées en moles/litre. Pour les gaz, cependant, les activités de chaque composant de la réaction sont exprimées en termes de pressions partielles plutôt que de molarité, où l’état standard est 1 bar de pression. Parfois, le symbole K_P est utilisé pour mettre en évidence les constantes d’équilibre calculées à partir des pressions partielles. Pour la réaction générale aA + bB ⇌ cC + dD, dans laquelle tous les composants sont des gaz, l’expression de la constante d’équilibre doit être écrite comme le rapport des pressions partielles des produits et des réactifs (chacun élevé à son coefficient dans l’équation chimique) :

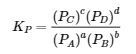
4.2.4

Ainsi, le PK pour la décomposition du N₂O₄ est le suivant :

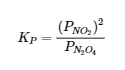
Le KP est une quantité sans unité parce que la quantité qui est effectivement utilisée pour le calculer est une “pression effective”, le rapport entre la pression mesurée et un état standard de 1 bar, qui produit une quantité sans unité. Mais qu’en est-il si nous devons décrire un équilibre de la phase gazeuse en unités de concentration ?

Comme les pressions partielles sont généralement exprimées en bar, la concentration molaire d’un gaz et sa pression partielle n’ont pas la même valeur numérique. Par conséquent, si nous recalculions K en utilisant les concentrations molaires (comme les solutés) au lieu des pressions partielles, nous obtiendrions une nouvelle constante d’équilibre, appelée K_C. La valeur numérique résultante de K_C serait très probablement différente de celle de K_P. Elles sont cependant liées par la constante idéale du gaz (R) et la température absolue (T) – ceci parce que la pression partielle d’un gaz est directement proportionnelle à sa concentration à température constante. Cette relation peut être dérivée de l’équation du gaz idéal, où M est la concentration molaire du gaz, nV.

PV = nRT

P = (n/V)RT

P = MRT

4.2.5

Ainsi, à température constante, la pression d’un gaz est directement proportionnelle à sa concentration.

Par conséquent, l’équation reliant K_C et K_P est dérivée comme suit. Pour la réaction en phase gazeuse mA + nB ⇌ xC + yD :

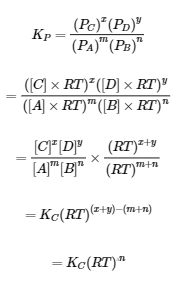
Par conséquent, la relation entre K_C et K_P est

4.2.6

où K_C est la constante d’équilibre exprimée en unités de concentration (mol/L), K_P est la constante d’équilibre exprimée en unités de pression (bars), la température est exprimée comme la température absolue en Kelvin, R est la constante de gaz idéale dans les unités appropriées (R = 0,083145 bar-L/(mol-K)) et Δn est la différence entre la somme des coefficients des produits gazeux et la somme des coefficients des réactifs gazeux dans la réaction (le changement en moles de gaz entre les réactifs et les produits). Pour la réaction en phase gazeuse mA + nB ⇌ xC + yD, nous avons

Δn = (x + y) – (m + n)

4.2.7

Selon l’équation ci-dessus, K_P = K_C uniquement si les moles de produits gazeux et de réactifs gazeux sont identiques (c’est-à-dire, Δn = 0).

Pour la décomposition du N2O4, il y a 2 moles de produit gazeux et 1 mole de réactif gazeux, donc Δn = 1. Donc, pour cette réaction,

Exemple 4.2.4 – Calcul du K_p

Écrivez les équations de conversion de K_C en K_P pour chacune des réactions suivantes :

(a) C₂H₆ (g) ⇌ C₂H₄ (_g) + H₂ (g)

(b) CO (g) + H₂O (g) ⇌ CO₂ (_g) + H₂ (g)

(c) N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

Qu’est-ce que le K_p à cette température ?

Solution

(a) Δn = (2) – (1) = 1

K_P = K_C(RT^)Δn = K_C(RT)¹ = K_C(RT)

(b) Δn = (2) – (2) = 0

K_P = K_C(RT^)Δn = K_C(RT)⁰ = K_C

(c) Δn = (2) – (1 + 3) = -2

K_P = K_C(RT^)Δn = K_C(RT^)-2 =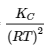

Vérifiez votre apprentissage 4.2.4 – Calcul du K_p

Écrivez les équations de conversion de K_C en K_P pour chacune des réactions suivantes, qui se produisent en phase gazeuse :

(a) 2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

(b) N₂O₄ (g) ⇌ 2 NO₂ (g)

(c) C₃H₈ (g) + 5 O₂ (g) ⇌ 3 CO_{2 (g)} + 4 H₂O (g)

Quelle serait la valeur du K_P à cette température ?

Réponse

(a) K_P = K_C(RT^)-1 ; (b) K_P = K_C(RT) ; (c) K_P = K_C(RT)

Exemple 4.2.5 – Calcul du K_p

Écrivez l’équation de la conversion de KC en KP pour la réaction suivante, qui se produit en phase gazeuse :

CS₂ (g) + 4 H₂ (g) ⇌ CH₄ (g) + 2 H₂S (g)

K_C est égal à 0,28 pour la réaction suivante à 900°C, qu’est-ce que le K_P à cette température ?

Solution

K_P = K_C(RT^)Δn = (0,28)[(0,0821)(1173)]^-2 = 3,0 × 10^-5

Vérifiez votre apprentissage 4.2.5 – Calcul du K_p

Écrivez l’équation de la conversion de K_C en K_P pour la réaction suivante, qui se produit en phase gazeuse :

CH₃OH (g) ⇌ CO (g) + 2 H₂ (g)

A 227°C, la réaction suivante a K_C = 0,0952, Quelle serait la valeur du K_P à cette température ?

Réponse

160 ou 1,6 × 10²

Exemple 4.2.6 – Calcul du K_P – Le processus Haber

La constante d’équilibre pour la réaction de l’azote et de l’hydrogène pour donner de l’ammoniac est de 0,118 à 745 K. L’équation d’équilibre est la suivante :

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

Quel est le K_P pour cette réaction à la même température ?

Solution

Cette réaction a 2 moles de produit gazeux et 4 moles de réactifs gazeux, donc Δn = (2 – 4) = -2. Nous connaissons K, et T = 745 K. Ainsi, nous avons ce qui suit :

Comme K_P est une quantité sans unité, la réponse est K_P = 3,16 × 10-5.

Vérifiez votre apprentissage 4.2.6 – Calcul du K_P – Le processus Haber

Calculer le K_P pour la réaction

2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

à 527°C, si K = 7,9 × 10⁴ à cette température.

Réponse

K_P = 1,2 × 10³

Équilibres hétérogènes

Le quotient de réaction, Q

Nous avons vu précédemment que la connaissance de l’ampleur de la constante d’équilibre dans un ensemble de conditions données permet aux chimistes de prédire l’ampleur d’une réaction. Souvent, cependant, les chimistes doivent décider si un système a atteint l’équilibre ou si la composition du mélange continuera à changer avec le temps.

Pour déterminer si un système a atteint l’équilibre, les chimistes utilisent une quantité appelée quotient de réaction (Q). L’expression du quotient de réaction a exactement la même forme que l’expression de la constante d’équilibre, sauf que Q peut être dérivé d’un ensemble de valeurs mesurées à tout moment pendant la réaction de tout mélange de réactifs et de produits, que le système soit ou non à l’équilibre. Par conséquent, pour la réaction générale suivante :

m A + n B ⇌ x C + y D

le quotient de réaction est défini comme suit :

4.2.7

Tout comme la constante d’équilibre, le quotient de réaction est sans dimension (pas d’unités) – ceci provient de l’utilisation des activités de l’espèce comme concentrations effectives. Comme précédemment, l’activité de chaque espèce participant à l’équilibre peut être représentée comme suit :

• Pour un soluté X, aX ≈ [X] en mol/L (notez que, là encore, cela ne s’applique pas aux solutions très concentrées)
• Pour les gaz, aX = PX en bar
• Pour les solides et les liquides purs, aX = 1

Exemple 4.2.6 – Rédaction des expressions du quotient de réaction

Écrivez l’expression du quotient de réaction pour chacune des réactions suivantes :

(a) 3 O₂ (g) ⇌ 2 O₃ (g)

(b) N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

(c) HCl (g) + NaOH (aq) ⇌ NaCl (aq) + H₂O (l)

Solution

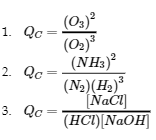
Vérifiez votre apprentissage 4.2.7 – Rédaction des expressions du quotient de réaction

Écrivez l’expression du quotient de réaction pour chacune des réactions suivantes :

            (a) 2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

(b) C₄H₈ (g) ⇌ 2 C₂H₄ (g)

(c) Cd₂⁺ (aq) + 4 Cl^– (aq) ⇌ CdCl₄^2- (aq)

Réponse

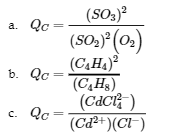
Exemple 4.2.8 – Évaluation du quotient de réaction

Selon cette équation, le dioxyde d’azote gazeux forme du tétroxyde de diazote:

2 NO₂ (g) ⇌ N₂O₄ (g)

Lorsqu’on ajoute 0,10 mol de NO2 dans un ballon de 1,0 L à 25°C, la concentration change de telle sorte qu’à l’équilibre, [NO2] = 0,016 mol/L et [N₂O₄] = 0,042 mol/L.

a) Quelle est la valeur du quotient de réaction en unités de concentration, Q_C, avant qu’une réaction ne se produise ?

(b) Quelle est la valeur de la constante d’équilibre en unités de concentration, K_C, pour la réaction ?

Solution

(a) Avant la formation de tout produit, [NO₂] =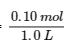 = 0,10 mol/L, et [N₂O₄] = 0 mol/L. Donc,

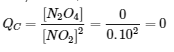
b) À l’équilibre, la valeur de la constante d’équilibre est égale à la valeur du quotient de réaction. À l’équilibre,

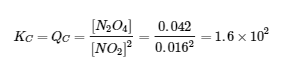
La constante d’équilibre est de 1,6 × 10².

Notez que l’analyse dimensionnelle suggère que l’unité pour cette valeur K_C devrait être (mol/L)^–1. Cependant, comme mentionné précédemment, il est courant d’omettre les unités pour les valeurs de K_C, puisque c’est l’ampleur d’une constante d’équilibre qui relaie les informations utiles.

Vérifiez votre apprentissage 4.2.8 – Évaluation du quotient de réaction

Pour la réaction 2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g), les concentrations à l’équilibre sont [SO₂] = 0,90 mol/L, [O₂] = 0,35 mol/L, et [SO₃] = 1,1 mol/L. Quelle est la valeur de la constante d’équilibre, K_C ?

Réponse

K_C = 4,3

Prévoir la direction du changement net à l’aide de Q

Pour comprendre comment l’information est obtenue à l’aide d’un quotient de réaction, examinons une fois de plus la dissociation du tétroxyde de diazote en dioxyde d’azote,

N₂O₄ (g) ⇌ 2 NO₂ (g)

pour laquelle K = 4,65 × 10^-3 à 298 K. Nous pouvons écrire Q_C pour cette réaction comme suit :

Le tableau suivant présente les données de trois expériences dans lesquelles des échantillons du mélange réactionnel ont été obtenus et analysés à des intervalles de temps équivalents, et les valeurs correspondantes de Q ont été calculées pour chacune d’entre elles. Chaque expérience commence avec des proportions différentes de produit et de réactif :

Expérience	NO2 (mol/L)	N2O4 (mol/L)
1	0	0.0400
2	0.0600	0
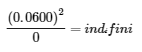3	0.0200	0.0600

Comme le montrent ces calculs, Q peut avoir n’importe quelle valeur numérique entre 0 et l’infini (indéfini), c’est-à-dire que Q peut être supérieur, inférieur ou égal à K. La comparaison des valeurs de Q et de K permet de déterminer si un mélange réactionnel est déjà à l’équilibre et, dans le cas contraire, de prédire comment sa composition changera avec le temps pour atteindre l’équilibre (c’est-à-dire si la réaction se déroulera à droite ou à gauche comme indiqué). Il suffit de se rappeler que la composition d’un système qui n’est pas à l’équilibre changera d’une manière qui fait que Q s’approche de K :

• Si Q = K, par exemple, alors le système est déjà à l’équilibre, et aucun autre changement dans la composition du système ne se produira à moins que les conditions ne soient modifiées.
• Si Q < K, alors le rapport entre les concentrations de produits et les concentrations de réactifs est inférieur au rapport à l’équilibre. Par conséquent, la réaction se déroulera à droite comme écrit, en formant des produits aux dépens des réactifs
• Si Q > K, alors le rapport entre les concentrations de produits et les concentrations de réactifs est supérieur à l’équilibre, de sorte que la réaction se déroulera à gauche comme écrit, en formant des réactifs au détriment des produits. Ces points sont illustrés graphiquement dans la figure 4.2.1.

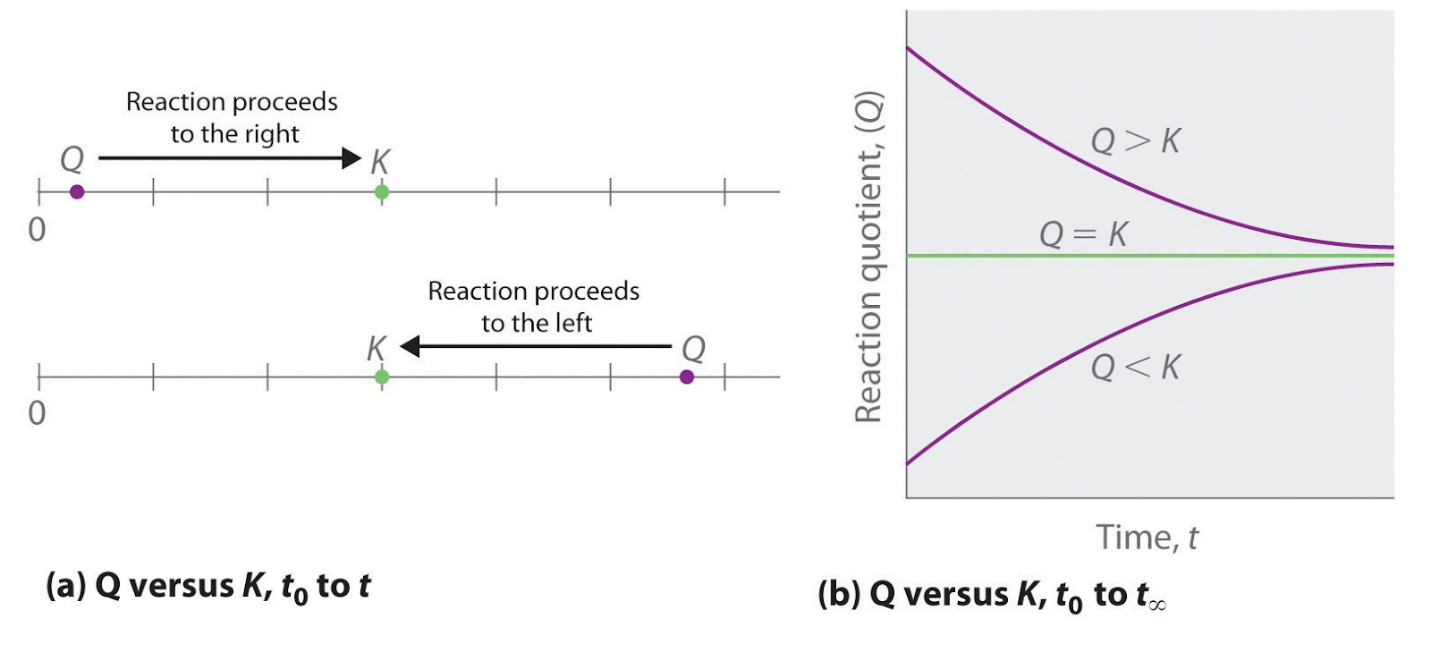
Figure 4.2.1. (a) Q et K sont tous deux représentés sous forme de points le long d’une ligne numérique : le système réagira toujours de la manière qui fait que Q se rapproche de K. (b) La modification de la composition d’un système en fonction du temps est illustrée pour les systèmes dont les valeurs initiales sont Q > K, Q < K et Q = K.

Exemple 4.2.9 – Prévoir la direction de la réaction

Voici les concentrations initiales de réactifs et de produits pour trois expériences impliquant cette réaction :

CO (g) + H₂O (g) ⇌ CO₂ (g) + H₂ (g)

K_C = 0,64

Déterminez dans quelle direction la réaction se déroule lorsqu’elle atteint l’équilibre dans chacune des trois expériences indiquées.

Solution

Expérience 1 :

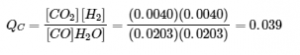
Qc < Kc (0,039 < 0,64)

La réaction va se déplacer vers la droite.

Expérience 2:

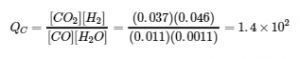
Qc > Kc (140 > 0,64)

La réaction va se déplacer vers la gauche.

Expérience 3:

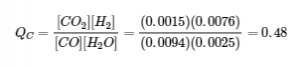
Qc < Kc (₀,48 < 0,64)

La réaction va se déplacer vers la droite.

Vérifiez votre apprentissage 4.2.9

Calculer le quotient de réaction et déterminer la direction dans laquelle chacune des réactions suivantes se déroulera pour atteindre l’équilibre.

(a) Un flacon de 1,00 L contenant 0,0500 mole de NO (g), 0,0155 mole de Cl₂ (g) et 0,500 mole de NOCl :

2 NO (g) + Cl₂ (g) ⇌ 2 NOCl (g)      Kc = 4.6 × 10⁴

b) Un flacon de 5,0 L contenant 17 g de NH₃, 14 g de N₂ et 12 g de H₂ :

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g) Kc = 0,060

c) Un flacon de 2,00 L contenant 230 g de SO3(g) :

2 SO₃ (g) ⇌ 2 SO₂ (g) + O₂ (g) Kc = 0,230

Réponse

(a) Qc = 6,45 × 10³, se déplace vers la droite. (b) Qc = 0,23, se décale vers la gauche. (c) Qc = 0, se décale vers la droite

Questions

★ Questions

1. Expliquez pourquoi un équilibre entre Br2 (l) et Br2 (g) ne serait pas établi si le contenant n’était pas étanche.
2. Si vous observez la réaction suivante à l’équilibre, est-il possible de dire si la réaction a commencé avec du NO2 pur ou avec du N2O4 pur ?

2 NO₂ (g) ⇌ N₂O₄ (g)

3. Parmi les règles de solubilité dont il a été question précédemment figure la déclaration : Les carbonates, les phosphates, les borates et les arséniates – à l’exception de l’ion ammonium et des métaux alcalins – sont insolubles.

         a. Écrivez l’expression de la constante d’équilibre de la réaction représentée                 par l’équation CaCO₃ (s) ⇌ Ca²⁺ (aq) + CO₃^2- (aq). Est-ce que Kc > 1, < 1, ou ≈ 1 ?           Expliquez votre réponse.

         b. Écrivez l’expression de la constante d’équilibre de la réaction représentée                 par l’équation 3 Ba²⁺ (aq) + 2 PO₄^3- (aq) ⇌ Ba₃(PO₄)₂ (s). Est-ce que Kc > 1, < 1,            ou ≈ 1 ? Expliquez votre réponse.

4. Le benzène est l’un des composés utilisés comme renforçateurs d’octane dans l’essence sans plomb. Il est fabriqué par la conversion catalytique de l’acétylène en benzène : 3 C₂H₂ (g) ⟶ C₆H₆ (g). Quelle valeur de K_C rendrait cette réaction la plus utile commercialement ? K_C ≈ 0,01, K_C ≈ 1, ou K_C ≈ 10. Expliquez votre réponse.

5. Montrer que l’équation chimique complète, l’équation ionique totale et l’équation ionique nette de la réaction représentée par l’équation KI (aq) + I₂ (aq) ⇌ KI₃ (aq) donnent la même expression pour le quotient de réaction. KI3 est composé des ions K+ et I^3-.

6. Pour qu’un titrage soit efficace, la réaction doit être rapide et le rendement de la réaction doit être essentiellement de 100 %. K_C > 1, < 1, ou ≈ 1 pour une réaction de titrage ?

7. Écrivez l’expression mathématique du quotient de réaction, Q_C, pour chacune des réactions suivantes :

a. CH₄ (g) + Cl₂ (g) ⇌ CH₃Cl (g) + HCl (g)

b. N₂ (g) + O₂ (g) ⇌ 2 NO (g)

c. 2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

d. BaSO₃ (s) ⇌ BaO (s) + SO₂ (g)

e. P₄ (g) + 5 O₂ (g) ⇌ P₄O₁₀ (s)

f. Br₂ (g) ⇌ 2 Br (g)

g. CH₄ (g) + 2 O₂ (g) ⇌ CO_{2 (}g) + 2 H₂O (l)

h. CuSO₄ ∙ 5 H₂O (s)  ⇌  CuSO₄ (s) + 5 H₂O (g)

8. Les concentrations ou pressions initiales des réactifs et des produits sont données pour chacun des systèmes suivants. Calculer le quotient de réaction et déterminer la direction dans laquelle chaque système va procéder pour atteindre l’équilibre.

         a. 2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g) K_c = 17 ; [NH₃] = 0,20 mol/L, [N₂] = 1,00 mol/L,             [H₂] = 1,00 mol/L

b. 2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g) K_P = 6,8 x 10⁴ ; pressions initiales : NH₃ = 2,00             atm, N₂ = 10,00 atm, H_{2 =} 10,00 atm

c. 2 SO₃ (g) ⇌ 2 SO₂ (g) +O₂ (g) Kc = 0,230 ; [SO₃] = 2,00 mol/L, [SO₂] = 2,00                 mol/L, [O₂] = 2,00 mol/L

d. 2 SO₃ (g) ⇌ 2 SO₂ (g) + O₂ (g) K_P = 6,5 atm ; pressions initiales : SO₂ = 1,00               atm, O₂ = 1,130 atm, SO₃ = 0 atm

e. 2 NO (g) + Cl₂ (g) ⇌ 2 NOCl (g) K_P = 2,5 x 10³ ; pressions initiales : NO = 1,00             atm, Cl₂ = 1,00 atm, NOCl = 0 atm

f. N₂ (g) + O₂ (g) ⇌ 2 NO (g) Kc = 0,050 ; [N₂] = 0,100 mol/L, [O₂] = 0,200                       mol/L, [NO] = 1,00 mol/L

★★ Questions

9. La réaction suivante a KP = 4,50 × 10-5 à 720 K.

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

Si une cuve de réaction est remplie de chaque gaz aux pressions partielles indiquées, dans quelle direction se déplacera-t-elle pour atteindre l’équilibre ? P(NH₃) = 93 atm, P(N₂) = 48 atm, et P(H₂) = 52

10. Déterminez si le système suivant est à l’équilibre. Si ce n’est pas le cas, dans quelle direction le système devra-t-il se déplacer pour atteindre l’équilibre ?

SO₂Cl₂ (g) ⇌ SO₂ (g) + Cl₂ (g)

[SO₂Cl₂] = 0,12 mol/L, [Cl₂] = 0,16 mol/L et [SO₂] = 0,050 mol/l. Kc pour la réaction est de 0,078.

11. Parmi les systèmes décrits à la question 8, lesquels donnent des équilibres homogènes ? Lesquels donnent des équilibres hétérogènes ?

12. Pour laquelle des réactions de la question 8 le KC (calculé à partir des concentrations) est-il égal au KP (calculé à partir des pressions) ?

13. Convertissez les valeurs de K_C en valeurs de K_P ou les valeurs de K_P en valeurs de K_C.

         a. N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)      K_C = 0,50 à 400◦C

b. H₂ (g) + I₂ (g) ⇌ 2 HI (g)      K_C = 50,2 sur 448◦C

c. Na₂SO₄ ∙ 10 H₂O (s) ⇌ Na₂SO₄ (s) + 10 H₂O (g)      K_P = 4,08 x 10^-25 à 25◦C

d. H₂O (l) ⇌ H₂O (g)      Kp = 0,122 à 50◦C

14. Quelle est la valeur de l’expression de la constante d’équilibre pour le changement H₂O (l) ⇌ H₂O (g) à 30 °C ? (Voir annexe F.)

15. Écrivez l’expression du quotient de réaction pour l’ionisation des HOCN dans l’eau.

16. Écrivez l’expression du quotient de réaction pour l’ionisation du NH₃ dans l’eau.

17. Quelle est la valeur approximative de la constante d’équilibre K_P pour la variation C₂H₅OC₂H₅ (l) ⇌ C₂H₅OC₂H₅ (g) à 25 °C. (La pression de vapeur a été décrite dans le chapitre précédent sur les liquides et les solides ; reportez-vous à ce chapitre pour trouver les informations pertinentes nécessaires à la résolution de ce problème).

Réponses

1. L’équilibre entre la phase liquide et la phase gazeuse ne peut être établi si le bouchon est retiré de la bouteille parce que le système n’est pas fermé ; l’un des composants de l’équilibre, la vapeur de Br₂, s’échapperait de la bouteille jusqu’à ce que tout le liquide ait disparu. Ainsi, plus de liquide s’évaporerait que ce qui peut se condenser de la phase gazeuse à la phase liquide.
2. Oui, en se basant sur le changement de couleur de la réaction, il est possible de déterminer la direction de la réaction.
3. (a) K_C = [Ca²⁺][CO₃^2-], K_C < 1 ;(b) K_C = 1 / [Ba²⁺]³[PO₄^3-]², K_C > 1
4.  Depuis 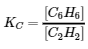une valeur de K_C ≈ 10 signifie que C₆H₆ prédomine sur C₂H₂. Dans un tel cas, la réaction serait commercialement réalisable si le taux d’équilibre est approprié.
5. Totale ionique : K+ (aq) + I- (aq) + I₂ (aq) ⇌ K+ (aq) + I^3- (aq), Ionique net : I- (aq) + I₂ (aq) ⇌ I^3- (aq)
6. KC > 1
7. 
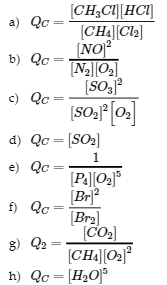
8. (a) Qc 25 produit à gauche ; (b) QP 0,22 produit à droite ; (c) Qc indéfini produit à gauche ; (d) QP 1,00 produit à droite ; (e) QP 0 produit à droite ; (f) Qc 4 produit à gauche
9. Le système va se déplacer vers les réactifs pour atteindre l’équilibre.
10. Le système n’est pas à l’équilibre puisque Q < K, donc la réaction va se déplacer vers la droite.
11. (a) Homogène, (b) Homogène, (c) Homogène, (d) Homogène, (e) Homogène, (f) Homogène
12. F est le seul où Kc = KP
13. (a) K_P = 1,6 × 10^-4 ; (b) K_P = 50,2 ; (c) Kc = 5,31 × 10^-39 ; (d) Kc = 4,60 × 10^-3
14. K_P = P_H2O = 0,042.
15. 
16. 
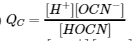
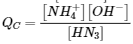
17. 0,717 atm