3.6 – Loi de Hess

Une façon de signaler la chaleur absorbée ou libérée serait de compiler un ensemble massif de tableaux de référence qui énumèrent les changements d’enthalpie pour toutes les réactions chimiques possibles, ce qui demanderait un effort incroyable. Heureusement, la loi de Hess, dont nous parlerons dans ce chapitre, nous permet de calculer la variation d’enthalpie pour pratiquement toutes les réactions chimiques imaginables en utilisant un ensemble relativement restreint de données tabulées, comme celles qui suivent :

Enthalpie de la combustion (ΔH_comb) : Changement d’enthalpie qui se produit lors d’une réaction de combustion. Les changements d’enthalpie ont été mesurés pour la combustion de pratiquement toutes les substances qui brûlent dans l’oxygène ; ces valeurs sont généralement rapportées comme l’enthalpie de combustion par mole de substance.

Enthalpie de la formation ₍ΔH_f) : Changement d’enthalpie dû à la formation d’une molécule à partir de ses éléments à l’état naturel dans des conditions standard (c’est-à-dire l’état dans lequel ils sont le plus stables à 25 C et 1 bar). Comme elles sont basées sur leurs éléments, l’enthalpie de formation pour les éléments à l’état naturel est toujours égale à zéro.

Enthalpie de la fusion (ΔH_fus) : Changement d’enthalpie qui accompagne la fusion (fusion) d’une mole d’une substance ; ces valeurs ont été mesurées pour presque tous les éléments et pour la plupart des composés simples.

Enthalpie de la vaporisation ₍ΔH_vap) : Changement d’enthalpie qui accompagne la vaporisation de 1 mole d’une substance. Le changement d’enthalpie qui accompagne la vaporisation d’une mole d’une substance ; ces valeurs ont également été mesurées pour presque tous les éléments et pour la plupart des composés volatils.

Enthalpie de la solution (ΔH_soln) : Changement d’enthalpie qui se produit lorsqu’une quantité déterminée de soluté se dissout dans une quantité donnée de solvant. L’enthalpie change lorsqu’une quantité spécifiée de soluté se dissout dans une quantité donnée de solvant.

Le changement d’enthalpie peut être visualisé à l’aide du diagramme énergétique suivant. Le changement d’énergie représente le changement d’enthalpie après qu’une réaction chimique ait eu lieu.

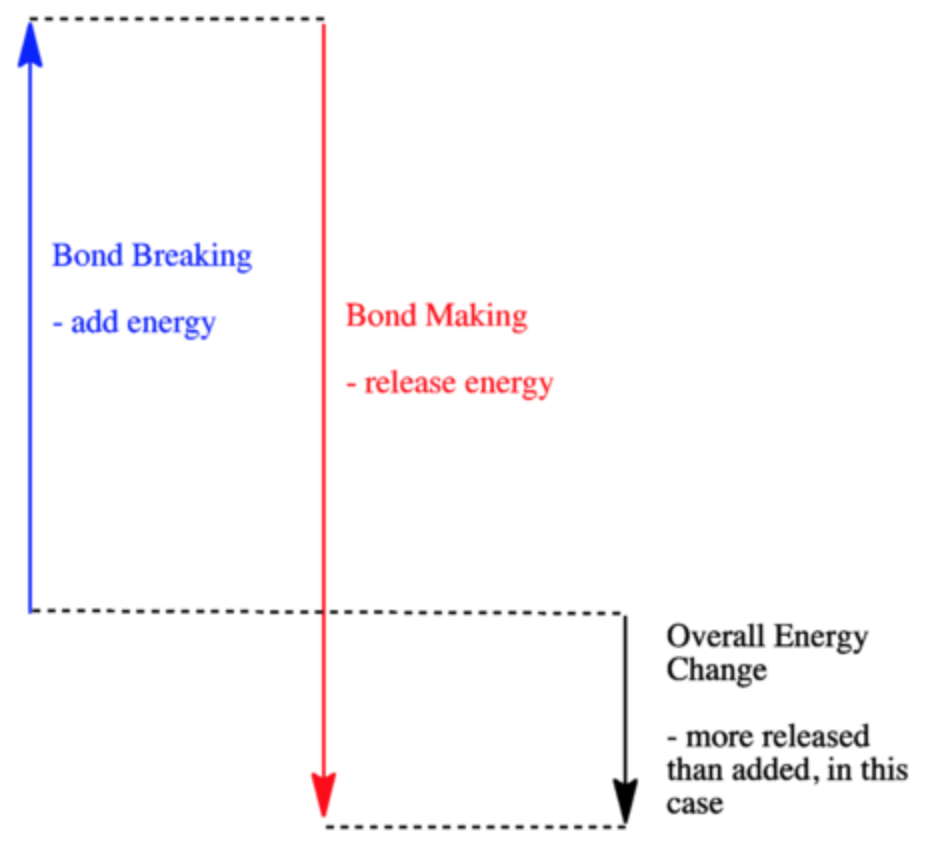
Figure 3.6.1. Diagramme de l’énergie de liaison montrant la variation d’énergie d’une réaction exothermique. (Chem Libre, de : https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/Fundamentals_of_Thermodynamics/Enthalpy_Changes_in_Reactions, Creative Commons)

Enthalpie de la combustion

L'enthalpie standard de combustion (ΔH°C) est le changement d’enthalpie lorsque 1 mole d’une substance brûle (se combine vigoureusement avec l’oxygène) dans des conditions d’état standard ; elle est parfois appelée “chaleur de combustion”. Par exemple, l’enthalpie de combustion de l’éthanol, -1366,8 kJ/mole, est la quantité de chaleur produite lorsqu’une mole d’éthanol subit une combustion complète à 25 °C et 1 bar de pression, donnant des produits également à 25 °C et 1 bar.

C₂H₅OH (l) + 3 O₂ (g)  →  2 CO₂ + 3 H₂O (l)     ΔH₂₉₈^∘ = – 1366,8 kJ

Il convient de noter qu’historiquement, l’unité de pression standard était 1 atmosphère (101,325 kPa), mais que l’UICPA l’a remplacée en 1982 par 1 bar (100 kPa). Sachez que ces deux valeurs sont encore couramment utilisées comme pression standard.

Les enthalpies de combustion de nombreuses substances ont été mesurées ; quelques-unes d’entre elles sont énumérées dans le tableau 3.6.1. De nombreuses substances facilement disponibles ayant de grandes enthalpies de combustion sont utilisées comme combustibles, notamment l’hydrogène, le carbone (comme le charbon ou le charbon de bois), et les hydrocarbures (composés contenant uniquement de l’hydrogène et du carbone), comme le méthane, le propane, et les principaux composants de l’essence.

Tableau 3.6.1 Enthalpies molaires standard de la combustion

Enthalpies molaires de combustion standard
Substance	Réaction à la combustion	Enthalpie de la combustion, ΔH°C (kJ à 25°C)
carbone	C (s) + O2 (g) → CO2 (g)	−393.5
hydrogène	H2 (g) + 1/2 O2 (g) →  H2O (l)	−285.8
magnésium	Mg (s) + 1/2 O2 (g) → MgO (s)	−601.6
soufre	S (s) + O2 (g) → SO2 (g)	−296.8
monoxyde de carbone	CO (g) + 1/2 O2 (g)  →  CO2 (g)	−283.0
méthane	CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l)	−890.8
acétylène	C2H2 (g) + 5/2 O2 (g) → 2 CO2 (g) + H2O (l)	−1301.1
éthanol	C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l)	−1366.8
méthanol	CH3OH (l) + 3/2 O2 (g) → CO2 (g) + 2 H2O (l)	−726.1
isooctane	C8H18 (l) + 25/2 O2 (g) → 8 CO2 (g) + 9 H2O (l)	−5461

Exemple 3.6.1 – Utilisation de l’enthalpie de la combustion

Comme l’illustre la figure 3.6.2, la combustion de l’essence est un processus hautement exothermique. Déterminons la quantité approximative de chaleur produite par la combustion de 1,00 L d’essence, en supposant que l’enthalpie de combustion de l’essence est la même que celle de l’isooctane, un composant commun de l’essence. La densité de l’isooctane est de 0,692 g/mL.

Figure 3.6.2. La combustion de l’essence est très exothermique. (crédit : modification du travail par “AlexEagle“/Flickr)

Solution

En partant d’une quantité connue (1,00 L d’isooctane), nous pouvons effectuer des conversions entre unités jusqu’à ce que nous arrivions à la quantité de chaleur ou d’énergie souhaitée. L’enthalpie de combustion de l’isooctane fournit l’une des conversions nécessaires. Le tableau ci-dessus donne cette valeur comme -5460 kJ pour une mole d’isooctane (C8H18).

L’utilisation de ces données,

La combustion de 1,00 L d’isooctane produit 33 100 kJ de chaleur. (Cette quantité d’énergie est suffisante pour faire fondre 99,2 kg de glace).

Note : Si vous faites ce calcul étape par étape, vous trouverez :

 

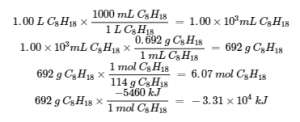
Vérifiez votre apprentissage 3.6.1 – Utilisation de l’enthalpie de la combustion

Quelle est la quantité de chaleur produite par la combustion de 125 g d’acétylène ?

Réponse

6,25 × 10³ kJ

Nouvelles technologies énergétiques à base d’algues (biocarburants)

Les réserves de combustibles fossiles diminuant et leur extraction devenant plus coûteuse, la recherche de sources de combustibles de remplacement pour l’avenir est en cours. Parmi les biocarburants les plus prometteurs figurent ceux qui sont dérivés des algues (figure 3.6.3.). Les espèces d’algues utilisées sont non toxiques, biodégradables et comptent parmi les organismes à croissance la plus rapide au monde. Environ 50 % du poids des algues est constitué d’huile, qui peut être facilement convertie en carburant comme le biodiesel. Les algues peuvent produire 26 000 gallons de biocarburant par hectare, soit beaucoup plus d’énergie par acre que les autres cultures. Certaines souches d’algues peuvent se développer dans une eau saumâtre qui n’est pas utilisable pour d’autres cultures. Les algues peuvent produire du biodiesel, du biogazoline, de l’éthanol, du butanol, du méthane et même du carburant pour avions.

Figure 3.6.3. (a) Les petits organismes d’algues peuvent être (b) cultivés en grandes quantités et éventuellement (c) transformés en un carburant utile tel que le biodiesel. (Crédit (a): modification des travaux de Micah Sittig ; crédit (b) : modification des travaux de Robert Kerton ; crédit (c) : modification des travaux de John F. Williams)

Selon le ministère américain de l’énergie, seuls 39 000 kilomètres carrés (environ 0,4 % de la masse terrestre des États-Unis ou moins de 1/7 de la zone utilisée pour la culture du maïs) peuvent produire suffisamment de carburant à base d’algues pour remplacer tout le carburant à base de pétrole utilisé aux États-Unis. Le coût des carburants à base d’algues est de plus en plus compétitif – par exemple, l’armée de l’air américaine produit du carburant pour avion à partir d’algues pour un coût total inférieur à 5 dollars américains le gallon. Le procédé utilisé pour produire du carburant à base d’algues est le suivant : cultiver les algues (qui utilisent la lumière du soleil comme source d’énergie et leCO₂ comme matière première) ; récolter les algues ; extraire les composés du carburant (ou les composés précurseurs) ; traiter si nécessaire (par exemple, effectuer une réaction de transestérification pour fabriquer du biodiesel) ; purifier et distribuer (figure 3.6.3.).

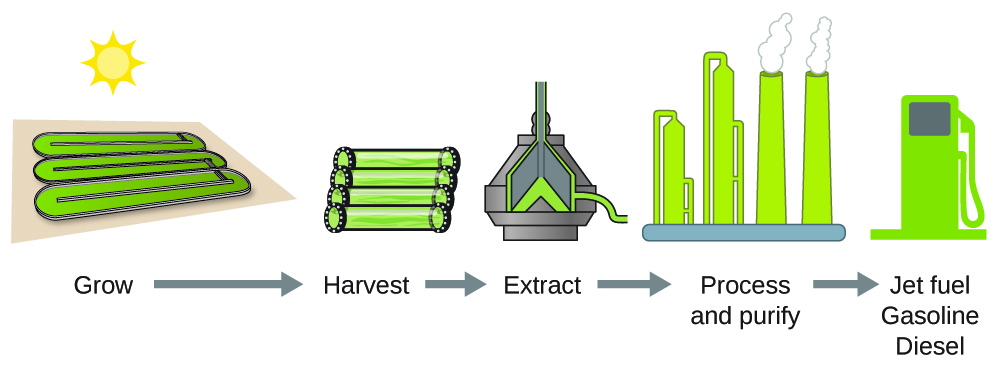
Figure 3.6.4. Les algues convertissent la lumière du soleil et le dioxyde de carbone en pétrole qui est récolté, extrait, purifié et transformé en une variété de carburants renouvelables.

Cliquez ici pour en savoir plus sur le processus de création de biocarburant à base d’algues.

Enthalpie standard de la formation

Enthalpie standard de formation ΔH_f^° est un changement d’enthalpie pour une réaction dans laquelle exactement une mole d’une substance pure est formée à partir d’éléments libres dans leurs états les plus stables dans des conditions standard. Ces valeurs sont particulièrement utiles pour calculer ou prévoir les changements d’enthalpie pour les réactions chimiques qui sont peu pratiques ou dangereuses à réaliser, ou pour les processus pour lesquels il est difficile de faire des mesures. Si nous disposons de valeurs pour les enthalpies standard de formation appropriées, nous pouvons déterminer le changement d’enthalpie pour toute réaction, ce que nous allons pratiquer ici dans cette section.

L’enthalpie standard de formation du CO₂ (g) est de -393,5 kJ/mol. C’est le changement d’enthalpie pour la réaction exothermique :

C (s) + O₂ (g) → CO₂ (g)     ΔH_f^∘ = ΔH₂₉₈^∘ = – 393,5 kJ

en commençant par les réactifs à une pression de 1 bar et 25 °C (avec le carbone présent sous forme de graphite, la forme de carbone la plus stable dans ces conditions) et en terminant par une mole de _CO2, également à 1 bar et 25 °C. Pour le dioxyde d’azote, NO₂ (g), ΔH_f° est de 33,2 kJ/mol. C’est le changement d’enthalpie pour la réaction :

Une équation de réaction avec 1/2 mole de N₂ et 1 mole de O₂ est correcte dans ce cas car l’enthalpie standard de formation se réfère toujours à 1 mole de produit, NO₂ (g).

Vous trouverez un tableau des enthalpies standard de formation de nombreuses substances courantes à l’annexe G. Ces valeurs indiquent que les réactions de formation vont de très exothermiques (telles que -2984 kJ/mole pour la formation de P4O10), à fortement endothermiques (telles que +226,7 kJ/mole pour la formation d’acétylène, _C2H2). Par définition, l’enthalpie standard de formation d’un élément sous sa forme la plus stable est égale à zéro dans des conditions standard, qui est de 1 bar pour les gaz et de 1 M pour les solutions. Les formes de référence utilisées pour la plupart des éléments sont simplement l’élément lui-même (par exemple l’argent : Ag (s)), mais certaines sont plus inhabituelles. Ces exceptions sont résumées dans le tableau ci-dessous.

Tableau 3.6.2 Formulaires de référence des éléments inhabituels

Formulaires de référence des éléments
Élément	Formulaire de référence
hydrogène	H2 (g)
azote	N2 (g)
oxygen	O2 (g)
fluor	F2 (g)
chlore	Cl2 (g)
brome	Br2 (l)
iode	I2 (s)
carbone	C (graphite, s)
phosphore	P (blanc, s)
soufre	S8 (s)

 

Exemple 3.6.2 – Évaluation d’une enthalpie de formation

L’ozone, O₃ (g)_, se forme à partir de l’oxygène, O₂ (g)_, par un processus endothermique. Le rayonnement ultraviolet est la source d’énergie qui déclenche cette réaction dans la haute atmosphère. En supposant que les réactifs et les produits de la réaction sont dans leur état standard, déterminez l’enthalpie standard de formation, _ΔHf° de l’ozone à partir des informations suivantes :

3 O₂ (g)  →  2 O₃ (g)     ΔH₂₉₈^∘ = + 286 kJ

Solution

_ΔHf° est le changement d’enthalpie pour la formation d’une mole d’une substance à son état standard à partir des éléments à leur état standard. Ainsi, ΔH_f° pour O₃ (g) est le changement d’enthalpie pour la réaction :

Pour la formation de 2 mol de O₃ (g), ΔH°₂₉₈ = + 286 kJ. Ce rapport, , la valeur de l’enthalpie de formation de l’O3_(g) peut être utilisée comme un facteur de conversion pour trouver la chaleur produite lorsque 1 mole d’O3(g) est formée, ce qui est l’enthalpie de formation de l’O₃ (g) :

Par conséquent, ΔH_f° [O₃ (g) ] = + 143 kJ/mol.

Vérifiez votre apprentissage 3.6.2 – Évaluation d’une enthalpie de formation

L’hydrogène gazeux, H₂, réagit de manière explosive avec le chlore gazeux, Cl_2, pour former du chlorure d’hydrogène, HCl (g). Quel est le changement d’enthalpie pour la réaction d’une mole de H₂ (g) avec une mole de Cl₂ (g) si les réactifs et les produits se trouvent dans des conditions d’état standard ? L’enthalpie standard de formation de HCl (g) est de -92,3 kJ/mol.

Réponse

H₂ (g) + Cl₂ (g) → 2 HCl (g)     ΔH₂₉₈^∘ = – 184,6 kJ

Exemple 3.6.3 – Rédaction d’équations de réaction pourΔH_f

Écrivez les équations de la réaction de la chaleur de formation pour :

(a) C₂H₅OH (l)

(b) Ca₃(PO₄)₂ (s)

Solution

Si l’on se souvient que les équations de réaction de ΔH_f° servent à former 1 mole du composé à partir de ses éléments constitutifs dans des conditions standard, nous avons :

         (a) 2 C (s, graphite) + 3 H₂ (g) + 1/2 O₂ (g)  →  C₂H₅OH (l)

         (b) 3 Ca (s) + 1/2 P₄ (s) + 4 O₂ (g)  →  Ca₃(PO₄)₂ (s)

Note : L’état standard du carbone est le graphite, et le phosphore existe sous forme de P₄.

Vérifiez votre apprentissage 3.6.3 – Rédaction d’équations de réaction pourΔH_f

Écrivez les équations de la réaction de la chaleur de formation pour :

(a) C₂H₅OC₂H₅ (l)

(b) Na₂CO₃ (s)

Réponse

         (a) 4 C (s, graphite) + 5 H₂ (g) + 1/2 O2 (g)  →  C₂H₅OC₂H (l)

         (b) 2 Na (s) + C (s, graphite) +  3/2 O₂ (g)  →  Na₃CO₃ (s)

La loi de Hess

Il y a deux façons de déterminer la quantité de chaleur impliquée dans un changement chimique : la mesurer expérimentalement ou la calculer à partir d’autres changements d’enthalpie déterminés expérimentalement. Certaines réactions sont difficiles, voire impossibles, à étudier et à mesurer de manière précise par voie expérimentale. Et même lorsqu’une réaction n’est pas difficile à réaliser ou à mesurer, il est pratique de pouvoir déterminer la chaleur impliquée dans une réaction sans avoir à réaliser une expérience.

Ce type de calcul implique généralement l’utilisation de la loi de Hess, qui stipule Si un processus peut être écrit comme la somme de plusieurs processus par étapes, le changement d’enthalpie du processus total est égal à la somme des changements d’enthalpie des différentes étapes. La loi de Hess est valable parce que l’enthalpie est une fonction d’état : Les changements d’enthalpie dépendent uniquement de l’endroit où un processus chimique commence et se termine, mais pas du chemin qu’il prend du début à la fin. Par exemple, on peut penser que la réaction du carbone avec l’oxygène pour former du dioxyde de carbone se produit soit directement, soit par un processus en deux étapes. Le processus direct est écrit :

C (s) + O₂ (g) → CO_{2 (}g)     ΔH₂₉₈^∘ = – 394 kJ

Dans ce processus en deux étapes, il y a d’abord formation de monoxyde de carbone :

C (s) + 1/2 O₂ (g)  → CO₂ (g)     ΔH₂₉₈^∘ = – 111 kJ

Ensuite, le monoxyde de carbone réagit encore pour former du dioxyde de carbone :

CO (g) + 1/2 O₂ (g) → CO₂ (g)     ΔH₂₉₈^∘ = – 283 kJ

L’équation décrivant la réaction globale est la somme de ces deux changements chimiques :

Étape 1 : C (s) + 1/2 O₂ (g)  → CO₂ (g)     ΔH₂₉₈^∘ = – 111 kJ

Étape 2 : CO (g) + 1/2 O₂ (g) → CO₂ (g)     ΔH₂₉₈^∘ = – 283 kJ

 

Somme : C (s) + O₂ (g) + CO (g) → CO (g) + CO₂ (g)

Étant donné que le CO produit à l’étape 1 est consommé à l’étape 2, la variation nette est :

C (s) + O₂ (g) → CO₂ (g)     ΔH₂₉₈^∘ = – 394 kJ

Selon la loi de Hess, le changement d’enthalpie de la réaction sera égal à la somme des changements d’enthalpie des étapes. Nous pouvons appliquer les données des enthalpies expérimentales de combustion du tableau 3.6.1 pour trouver le changement d’enthalpie de l’ensemble de la réaction à partir de ses deux étapes :

 C (s) + 1/2 O₂ (g)  → CO₂ (g)     ΔH₂₉₈^∘ = – 111 kJ

Le résultat est présenté dans la figure 3.6.5. Nous voyons que ΔH de la réaction globale est la même qu’elle se produise en une ou deux étapes (c’est-à-dire qu’il s’agit d’une fonction d’état). Ce résultat (ΔH global de la réaction = somme des valeurs de ΔH pour les “étapes” de la réaction globale) est vrai en général pour les processus chimiques et physiques.

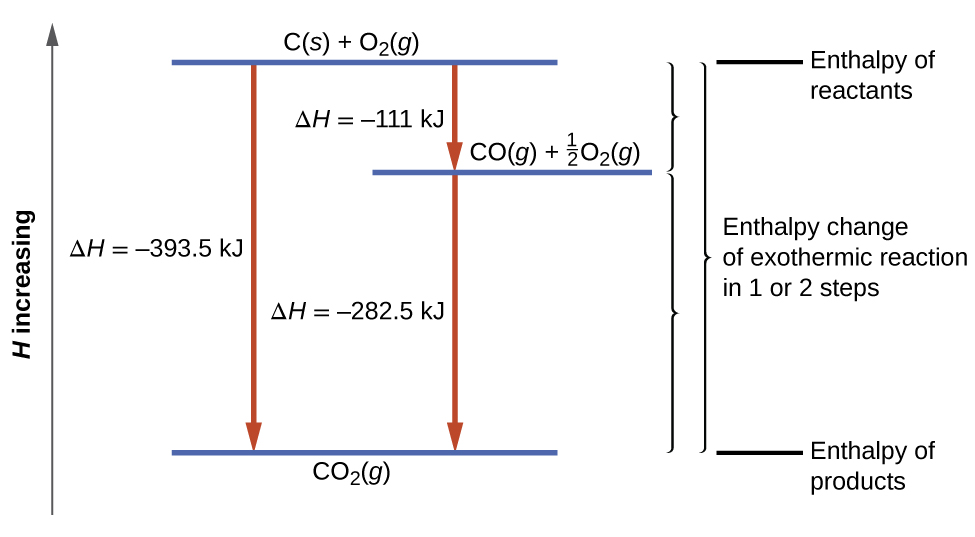
Figure 3.6.5. La formation de _CO2(g) à partir de ses éléments peut être considérée comme se déroulant en deux étapes, qui s’additionnent pour former la réaction globale, telle que décrite par la loi de Hess. Les lignes bleues horizontales représentent les enthalpies. Pour un processus exothermique, les produits sont à une enthalpie inférieure à celle des réactifs.

Avant de poursuivre notre pratique en utilisant la loi de Hess, rappelons deux caractéristiques importantes de ΔH.

ΔH est directement proportionnel aux quantités de réactifs ou de produits. Par exemple, le changement d’enthalpie pour la réaction formant 1 mole de NO₂ (g) est de +33,2 kJ :

Lorsque 2 moles de NO₂ (deux fois plus) sont formées, le ΔH sera deux fois plus grand :

N₂ (g) + 2 O₂ (g) → 2 NO₂ (g)     ΔH = +66,4 kJ

En général, si nous multiplions ou divisons une équation par un nombre, alors la variation d’enthalpie doit également être multipliée ou divisée par le même nombre.

ΔH pour une réaction dans un sens est égal en magnitude et de signe opposé à ΔH pour la réaction dans le sens inverse. Par exemple, étant donné que

H₂ (g) + Cl₂ (g) → 2 HCl (g)     ΔH = – 184,6 kJ

Ensuite, pour la réaction “inverse”, le changement d’enthalpie est également “inversé” :

2 HCl (g) → H₂ (g) + Cl₂ (g)     ΔH = + 184,6 kJ

Exemple 3.6.4 – Calcul par étapes de ΔH_{f° en} utilisant la loi de Hess

Déterminer l’enthalpie de formation, ΔH_f°, du FeCl₃ (s) à partir des changements d’enthalpie du processus en deux étapes suivantes qui se produit dans des conditions d’état standard :

Fe (s) + Cl₂ (g) → FeCl₂ (s)     ΔH = – 341,8 kJ

FeCl₂ (s) + 1/2 Cl₂ (g) → FeCl₃ (s)     ΔH = – 57,7 kJ

Solution

Nous essayons de trouver l’enthalpie standard de formation de FeCl₃ (s), qui est égale à ΔH° pour la réaction :

Fe (s) + 3/2 Cl₂ (g) → FeCl₃ (s)     ΔH^∘ = ?

En examinant les réactions, nous constatons que la réaction pour laquelle nous voulons trouver ΔH° est la somme des deux réactions dont les valeurs de ΔH sont connues, nous devons donc additionner leurs enthalpies :

Fe (s) + Cl₂ (g) → FeCl₂ (s)     ΔH∘ = – 341,8 kJ

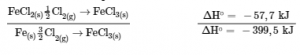
L’enthalpie de formation, ΔH_f°, de FeCl₃ (s) est de -399,5 kJ/mol.

Vérifiez votre apprentissage 3.6.4 – Calcul par étapes de ΔH_{f° en} utilisant la loi de Hess

Calculer ΔH pour le processus :

N₂ (g) + 2 O₂ (g) → 2 NO₂ (g)

à partir des informations suivantes :

N₂ (g) + 2 O₂ (g) → 2 NO₂ (g)     ΔH = 180,5 kJ

NON (g) + 1/2 O₂ (g)  →  NO₂ (g)     ΔH = – 57.06 kJ

Réponse

66,4 kJ

Voici un exemple moins simple qui illustre le processus de réflexion nécessaire à la résolution de nombreux problèmes de la loi de Hess. Il montre comment on peut trouver de nombreuses enthalpies standard de formation (et d’autres valeurs de ΔH) si elles sont difficiles à déterminer expérimentalement.

Exemple 3.6.5 – Un problème plus difficile avec la loi de Hess

Le monofluorure de chlore peut réagir avec le fluor pour former du trifluorure de chlore :

(i) ClF (g) + F₂ (g) → ClF₃ (g)     ΔH^∘ = ?

Utilisez les réactions ici pour déterminer le ΔH° pour la réaction (i) :

(ii) 2 OF₂ (g) → O₂ (g) + 2 F₂ (g)     ΔH_(ii)^∘ = – 49,4 kJ

(iii) 2 ClF₂ (g) + O₂ (g) → Cl₂O (g) + OF₂ (g)     ΔH_(iii)^∘ = + 205,6 kJ

(iv) ClF₃ (g) + O₂ (g) → 1/2 Cl₂O (g) + 3/2 OF₂ (g)     ΔH_(iv)^∘ = + 266,7 kJ

Solution

Notre objectif est de manipuler et de combiner les réactions (ii), (iii) et (iv) de manière à ce qu’elles s’additionnent pour former la réaction (i). En allant de gauche à droite dans (i), nous voyons d’abord que le ClF (g) est nécessaire comme réactif. Cela peut être obtenu en multipliant la réaction (iii) par 1/2 ce qui signifie que la variation de ΔH° est également multipliée par 1/2:

ClF (g) + 1/2 O₂ (g) → 1/2 Cl₂O (g) + 1/2 OF₂ (g)     

ΔH_(iii)^∘ = 1/2(+ 205,6 kJ) = + 102,8 kJ

Ensuite, nous voyons que le F₂ est également nécessaire en tant que réactif. Pour cela, il faut inverser et réduire de moitié la réaction (ii), ce qui signifie que le ΔH° change de signe et est réduit de moitié :

Pour obtenir la ClF3 en tant que produit, inverser (iv), en changeant le signe de ΔH° :

Vérifiez maintenant que ces réactions s’additionnent pour donner la réaction que nous souhaitons :

1/2 O₂ (g) + F₂ (g) → OF₂ (g)     ΔH(ii)∘ = + 24,7 kJ

Réactifs 1/2 O₂ et 1/2 O₂ annuler produit O₂ ; produit 1/2 Cl₂O annule le réactif 1/2 Cl₂O ; et réactif 3/2 OF₂ est annulé par les produits 1/2 OF₂ et OF₂. Il ne reste donc que les réactifs ClF (g) et F₂ (g) et le produit ClF₃ (g), qui sont ce que nous voulons. Puisque la somme de ces trois réactions modifiées donne la réaction qui nous intéresse, la somme des trois valeurs modifiées de ΔH° donnera le ΔH° souhaité :

ΔH^∘ = (+ 102,8 kJ) + (24,7 kJ) + (- 266,7 kJ) = – 139,2 kJ

 

Vérifiez votre apprentissage 3.6.6 – Un problème plus difficile avec la loi de Hess

Le chlorure d’aluminium peut être formé à partir de ses éléments :

(i) 2 Al (s) + 3 Cl₂ (g)  →  2 AlCl₃ (s)       ΔH∘=?

Utilisez les réactions ici pour déterminer le ΔH° pour la réaction (i) :

(ii) HCl (g) → HCl (aq)     ΔH_(ii)^∘ = – 74,8 kJ

(iii) H₂ (g) + Cl₂ (g) → 2 HCl (g)      ΔH_(iii)^∘ = – 185 kJ

(iv) AlCl₃ (aq) → AlCl₃ (s)      ΔH_(iv)^∘ = + 323 kJ/mol

(v) 2 Al (s) + 6 HCl (aq) → 2 AlCl₃ (aq) + 3 H₂ (g)     ΔH_(v)^∘ = + 1049 kJ

Réponse

-1407 kJ

Nous pouvons également utiliser la loi de Hess pour déterminer le changement d’enthalpie de toute réaction si les enthalpies correspondantes de formation des réactifs et des produits sont disponibles. Les réactions par étapes que nous considérons sont (i) des décompositions des réactifs en leurs éléments constitutifs (pour lesquels les changements d’enthalpie sont proportionnels au négatif des enthalpies de formation des réactifs), suivies par (ii) des recombinaisons des éléments pour donner les produits (avec des changements d’enthalpie proportionnels aux enthalpies de formation des produits). Le changement d’enthalpie standard de la réaction globale est donc égal à (ii) la somme des enthalpies de formation standard de tous les produits plus (i) la somme des négatifs des enthalpies de formation standard des réactifs. Cette formule est généralement légèrement réorganisée pour s’écrire comme suit, ∑ représentant “la somme de” et n représentant les coefficients stœchiométriques :

ΔH_réaction^∘ = Σn × ΔH_f^∘(produits) – Σn × ΔH_f^∘(réactifs)

L’exemple suivant montre en détail pourquoi cette équation est valable, et comment l’utiliser pour calculer le changement d’enthalpie pour une réaction d’intérêt.

Exemple 3.6.7 – Utiliser la loi de Hess

Quel est le changement d’enthalpie standard pour la réaction :

3 NO₂ (g) + H₂O (l) → 2 HNO₃ (aq) + NO (g)     ΔH^∘ = ?

Solution :

Utilisez la forme spéciale de la loi de Hess donnée précédemment :

ΔH_réaction^∘ = Σn × ΔH_f^∘(produits) – Σn × ΔH_f^∘(réactifs)

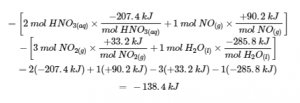
Solution 

Soutenir la validité de l’équation générale

On peut aussi écrire cette réaction comme la somme des décompositions de 3 NO₂ (g) et 1 H₂O (l) en leurs éléments constitutifs, et la formation de 2 HNO₃ (aq) et 1 NO (g) à partir de leurs éléments constitutifs. Nous avons écrit ces réactions et noté leurs relations avec les valeurs de _ΔHf° pour ces composés (de l’annexe G) :

3 NO₂ (g) → 3/2 N₂ (g) + 3 O₂ (g)      ΔH₁^∘ = – 99,6 kJ

H₂O (l) → H₂ (g) + 1/2 O₂ (g)     ΔH₂^∘ = + 285,8 kJ [- 1 × ΔH_f^∘(H₂O)]

H₂ (g) + N₂ (g) + 1/2 O₂ (g) → 2 HNO₃ (aq)     

ΔH₃^∘ = – 414,8 kJ [- 1 × ΔH_f^∘(HNO₃)]

En additionnant ces équations de réaction, on obtient la réaction qui nous intéresse :

3 NO₂ (g) + H₂O (l) → 2 HNO₃ (aq) + NO (g)

La somme de leurs changements d’enthalpie donne la valeur que nous voulons déterminer :

ΔH_rxn^∘ = ΔH₁^∘ + ΔH₂^∘ + ΔH₃^∘ + ΔH₄^∘ = (- 99.6 kJ) + (+ 285.8 kJ) +(- 414.8 kJ) + (+ 90.2 kJ)

= – 138,4 kJ

Le changement d’enthalpie standard pour cette réaction est donc ΔH° = -138,4 kJ.

Notez que ce résultat a été obtenu en (1) multipliant le _ΔHf° de chaque produit par son coefficient stœchiométrique et en additionnant ces valeurs, (2) en multipliant le _ΔHf° de chaque réactif par son coefficient stœchiométrique et en additionnant ces valeurs, puis (3) en soustrayant le résultat trouvé en (2) du résultat trouvé en (1). C’est également la procédure à suivre pour utiliser l’équation générale, comme indiqué.

Pour une explication plus approfondie de cette approche, consultez la vidéo suivante.

Vérifiez votre apprentissage 3.6.7 – Utiliser la loi de Hess

Calculer la chaleur de combustion d’une mole d’éthanol, C₂H₅OH (l), lorsque H₂O (l) et CO₂ (g) sont formés. Utilisez les enthalpies de formation suivantes : C₂H₅OH (l), -278 kJ/mole ; H₂O (l), -286 kJ/mole ; et CO₂ (g), -394 kJ/mole.

Réponse

-1368 kJ/mol

Questions

★ Questions

1. Quelle quantité de chaleur est produite lorsque 100 ml de HCl 0,250 M (densité, 1,00 g/mL) et 200 ml de NaOH 0,150 M (densité, 1,00 g/mL) sont mélangés ?

HCl (aq) + NaOH (aq) → NaCl (aq) + H₂O (l)     ΔH₂₉₈^∘ = – 58 kJ

Si les deux solutions sont à la même température et que la capacité thermique des produits est de 4,19 J/g °C, de combien la température augmentera-t-elle ? Quelle hypothèse avez-vous faite dans votre calcul?

   2. Avant l’introduction des chlorofluorocarbures, le dioxyde de soufre (enthalpie         de vaporisation, 6,00 kcal/mol) était utilisé dans les réfrigérateurs domestiques.         Quelle masse de SO₂ doit être évaporée pour éliminer autant de chaleur que               l’évaporation de 1,00 kg de CCl₂F₂ (l’enthalpie de vaporisation est de 17,4 kJ/mol) ?     Les réactions de vaporisation du SO₂ et du CCl₂F₂ sont respectivement le SO₂             (l)  _⟶  SO₂ (g) et le CCl₂F (l)⟶CCl₂F_{2 (}g).

   3. Les maisons peuvent être chauffées en pompant de l’eau chaude par des                 radiateurs. Quelle masse d’eau fournira la même quantité de chaleur lorsqu’elle         est refroidie de 95,0 à 35,0 °C, que la chaleur fournie lorsque 100 g de vapeur sont     refroidis de 110 °C à 100 °C.

   4. L’enthalpie standard de formation de _H2O (g) diffère-t-elle de celle de ΔH° pour     la réaction 2 H₂ (g) + O₂ (g) ⟶ 2 H₂O (g) ?

   5. Joseph Priestly a préparé de l’oxygène en 1774 en chauffant de l’oxyde de                mercure(II) rouge avec la lumière du soleil focalisée à travers une lentille. Quelle          quantité de chaleur est nécessaire pour décomposer exactement 1 mole de HgO        (s) rouge en Hg (l) et O₂ (g) dans des conditions normales ?

   6. Combien de kilojoules de chaleur seront libérées lorsqu’exactement une mole         de manganèse, Mn, est brûlée pour former du Mn3O4(s) dans des conditions             d’état standard ?

★★ Questions

   7. La séquence de réactions suivante se produit lors de la production commerciale     d’acide nitrique aqueux :

4 NH₃ (g) + 5 O₂ (g) → 4 NO (g) + 6 H₂O (l)     ΔH = -907 kJ

2 NO (g) + O₂ (g) → 2 NO (g)     ΔH = – 113 kJ

3 NO₂ + H₂O (l) → 2 HNO₃ (aq) + NO (g)      ΔH = – 139 kJ

Déterminez la variation totale d’énergie pour la production d’une mole d’acide nitrique aqueux par ce procédé.

   8. Le graphite et le diamant brûlent tous deux.

C (s, diamant) + O₂ (g) → CO₂ (g)

Pour la conversion du graphite en diamant :

C (s, diamant) → CO₂ (g)     ΔH₂₉₈^∘ = 1,90 kJ

Qu’est-ce qui produit le plus de chaleur, la combustion du graphite ou la combustion du diamant ?

   9. À partir des chaleurs molaires de formation de l’annexe G, déterminez la                 quantité de chaleur nécessaire pour évaporer une mole d’eau :

H₂O (l) → H₂O (g)

   10. Calculer ΔH298∘ pour le processus

Sb (s) + 5/2 Cl₂ (g) → SbCl5 (g)

à partir des informations suivantes :

Sb (s) + 3/2 Cl₂ (g) → SbCl₅ (g)     ΔH₂₉₈^∘ = – 314 kJ

SbCl₃ (s) + Cl₂ (g) → SbCl₅ (g)     ΔH₂₉₈^∘ = – 80 kJ

   11. Calculer ΔH₂₉₈^° pour le processus

Zn (s) + S (s) + 2 O₂ (g) → ZnSO₄ (s)

à partir des informations suivantes :

Zn (s) + S (s) → ZnS (s)     ΔH₂₉₈^∘ = – 206,0 kJ

ZnS (s) + 2 O₂ (g) → ZnSO₄ (s)     ΔH₂₉₈^∘ = – 776,8 kJ

   12. Calculer l’enthalpie molaire standard de formation de NO(g) à partir des                  données suivantes :

N₂ (g) + 2 O₂ → 2 NO₂ (g)     ΔH₂₉₈^∘ = 66,4 kJ

2 NO (g) + O₂ → 2 NO₂ (g)     ΔH₂₉₈^∘ = – 114,1 kJ

   13. En utilisant les données de l’annexe G, calculez la variation d’enthalpie                     standard pour chacune des réactions suivantes :

         a. N₂ (g) + O₂ (g) → 2 NO (g)

         b. Si (s) + 2 Cl₂ (g) → SiCl₄ (g)

         c. Fe₂O₃ (s) + 3 H₂ (g) → 2 Fe (s) + 3 H₂O (l)

         d. 2 LiOH (s) + Co₂ (g) → Li₂CO₃ (s) + H₂O (g)

   14. Les réactions suivantes peuvent être utilisées pour préparer des échantillons       de métaux. Déterminez le changement d’enthalpie dans des conditions d’état             standard pour chacune d’entre elles.

         a. 2 Ag₂O (s) → 4 Ag (s) + O₂ (g)

         b. SnO (s) + CO (g) → Sn (s) + CO₂ (g)

         c. Cr₂O₃ (s) + 3 H₂ (g) → 2 Cr (s) + 3 H₂O (l)

         d. 2 Al (s) + Fe₂O₃ (s) → Al₂O₃ (s) + 2 Fe (s)

   15. Calculer l’enthalpie de combustion du propane, C₃H₈ (g), pour la formation de        H₂O (g) et CO₂ (g). L’enthalpie de formation du propane est de -104 kJ/mol.

   16. Le propane et le butane sont tous deux utilisés comme combustibles gazeux.       Quel composé produit le plus de chaleur par gramme lorsqu’il est brûlé ?

★★★ Questions

   17. L’éthanol, le C₂H₅OH, est utilisé comme carburant pour les véhicules à moteur,      notamment au Brésil.

         a. Écrivez l’équation équilibrée pour la combustion de l’éthanol en CO₂(g) et                 H₂O(g), et, en utilisant les données de l’annexe G, calculez l’enthalpie de                       combustion d’une mole d’éthanol.

         b. La densité de l’éthanol est de 0,7893 g/mL. Calculer l’enthalpie de                             combustion d’exactement 1 L d’éthanol.

         c. En supposant que le kilométrage d’une automobile est directement                           proportionnel à la chaleur de combustion du carburant, calculez la distance                 qu’une automobile pourrait parcourir avec 1 L d’essence par rapport à 1 L                     d’éthanol. Supposons que l’essence possède la chaleur de combustion et la                 densité du n-octane, C8H18 (ΔHf°=-208,4kJ/mol ; densité = 0,7025 g/mL).

   18. Parmi les substances qui réagissent avec l’oxygène et qui ont été considérées        comme des carburants potentiels pour fusée, on trouve le diborane [_B2H6, produit      B₂O₃ (s) et H₂O (g)], le méthane [CH₄, produit CO₂ (g) et H₂O (g)], et l’hydrazine        [N₂H₄, produit N₂ (g) et H₂O (g)]. Sur la base de la chaleur dégagée par 1,00 g de        chaque substance dans sa réaction avec l’oxygène, lequel de ces composés offre        les meilleures possibilités en tant que carburant pour fusée ? Le ΔH_f^° de B₂H₆ (g),      CH₄ (g), et N₂H₄ (l) se trouve à l’annexe G.

   19. L’oxydation du sucre glucose, _C6H12O6, est décrite par l’équation suivante :

C₆H₁₂O₆ (s) + 6 O₂ (g) → 6 CO₂ (g) + 6 H₂O (l)     ΔH = – 2816 kJ

Le métabolisme du glucose donne les mêmes produits, bien que le glucose réagisse avec l’oxygène en une série d’étapes dans le corps.

         a. Quelle quantité de chaleur en kilojoules peut être produite par le                               métabolisme de 1,0 g de glucose ?

         b. Combien de calories peuvent être produites par le métabolisme de 1,0 g de             glucose ?

   20. Au cours d’un récent mois d’hiver à Sheboygan, dans le Wisconsin, il a fallu          obtenir 3500 kWh de chaleur fournie par un fourneau à gaz naturel d’une                    efficacité de 89% pour maintenir une petite maison au chaud (l’efficacité d’un            fourneau à gaz est le pourcentage de la chaleur produite par la combustion qui est    transféré dans la maison).

         a. Supposons que le gaz naturel soit du méthane pur et déterminons le                         volume de gaz naturel en pieds cubes qui était nécessaire pour chauffer la                   maison. La température moyenne du gaz naturel était de 56 °F ; à cette                       température et à une pression de 1 atm, le gaz naturel a une densité de 0,681              g/L.

         b. Combien de gallons de GPL (gaz de pétrole liquéfié) seraient nécessaires                 pour remplacer le gaz naturel utilisé ? Supposons que le GPL soit du propane             liquide [C₃H₈ : densité, 0,5318 g/mL ; enthalpie de combustion, 2219 kJ/mol                   pour la formation de CO₂ (g) et H₂O (l)] et que le four utilisé pour brûler le GPL           ait la même efficacité que le four à gaz.

         c. Quelle est la masse de dioxyde de carbone produite par la combustion du                 méthane utilisé pour chauffer la maison ?

         d. Quelle est la masse d’eau produite par la combustion du méthane utilisé                  pour chauffer la maison ?

         e. Quel volume d’air est nécessaire pour fournir l’oxygène nécessaire à la                     combustion du méthane utilisé pour chauffer la maison ? L’air contient 23%               d’oxygène en masse. La densité moyenne de l’air au cours du mois était de                  1,22 g/L.

         f. Combien de kilowattheures (1 kWh = 3,6 × 10⁶ J) d’électricité seraient                        nécessaires pour fournir la chaleur nécessaire au chauffage de la maison ?                    Notez que l’électricité est efficace à 100 % pour produire de la chaleur à                        l’intérieur d’une maison.

         g. Bien que l’électricité soit efficace à 100 % pour produire de la chaleur à                     l’intérieur d’une maison, la production et la distribution de l’électricité ne le                sont pas à 100 %. L’efficacité de la production et de la distribution de                            l’électricité produite dans une centrale au charbon est d’environ 40 %. Un                    certain type de charbon fournit 2,26 kWh par livre lors de la combustion.                      Quelle masse de ce charbon en kilogrammes sera nécessaire pour produire                  l’énergie électrique nécessaire au chauffage de la maison si l’efficacité de la                  production et de la distribution est de 40 % ?

Réponses

3. 7.43 g

4. Non.

5. 90,8 kJ

6. 459,6 kJ

7. -495 kJ/mol

8. La combustion du diamant produit plus de chaleur

9. 44,01 kJ/mol

10. -394 kJ

11. – 207 kJ

12. 90,3 mol-1 de NO

13. (a) 90,4 kJ/mol, (b) 105 kJ/mol, (c) -538,37 kJ/mol, (d) 94,49 kJ/mol

14. (a) 62,2 kJ/mol, (b) 3,2 kJ/mol, (c) 271 kJ/mol, (d) -847,6 kJ/mol

15. – 2044 kJ

16. Propane

17. (a) C₂H₅OH + 3 O₂ (g) → 2 CO₂ (g) + 3 H₂O (g), -1234,8 kJ/mol, (b) -21187,56 kJ, (c) 44% plus loin

18. En partant du principe que le meilleur carburant pour fusée est celui qui dégage le plus de chaleur, le B₂H₆ est le candidat idéal.

19. (a) 15,63 kJ/g, (b) 3,74 cal/g

20. (a) 13260 pieds cubes, (b) 141,2 gallons, (c) 701,52 kg, (d) 574,32 kg, (e) 3635637,26 L, (f) 3500 kWh, (g) 1756,34 kg