3.5 – Calorimétrie

Une technique que nous pouvons utiliser pour mesurer la quantité de chaleur impliquée dans un processus chimique ou physique est connue sous le nom de calorimétrie. La calorimétrie est utilisée pour mesurer la quantité de chaleur transférée vers ou depuis une substance. Pour ce faire, la chaleur est échangée avec un objet calibré (calorimètre). Le changement de température mesuré par le calorimètre est utilisé pour calculer la quantité de chaleur transférée par le processus étudié. La mesure du transfert de chaleur par cette approche nécessite la connaissance et la compréhension d’un système et de son environnement (voir “Introduction à la thermochimie” pour revoir la terminologie du système et de l’environnement). Comme nous l’avons vu dans les sections précédentes, l’énergie dans l’univers n’est ni créée ni détruite, mais seulement transférée. Cela implique que le changement d’énergie interne de l’univers doit être nul – tout est conservé là où il n’y a ni gain ni perte d’énergie :

ΔU_universe = 0

En plus de cela, nous devons également comprendre quelques autres concepts que nous allons passer en revue dans cette section pour saisir le concept de calorimétrie.

Capacités thermiques

Nous présentons maintenant deux concepts utiles pour décrire le flux de chaleur et le changement de température. La capacité thermique (C) d’un corps de matière est la quantité de chaleur (q) qu’il absorbe ou libère lorsqu’il subit un changement de température (ΔT) de 1 degré Celsius (ou équivalent, 1 kelvin) :

C = q/ΔT

Équation 3.5.1 Capacité calorifique

La capacité thermique est déterminée par le type et la quantité de substance qui absorbe ou libère de la chaleur. Il s’agit donc d’une propriété étendue – sa valeur est proportionnelle à la quantité de la substance.

Par exemple, considérez les capacités thermiques de deux poêles à frire en fonte. La capacité thermique de la grande poêle est cinq fois supérieure à celle de la petite poêle car, bien que les deux soient faites du même matériau, la masse de la grande poêle est cinq fois supérieure à celle de la petite poêle. Plus de masse signifie que plus d’atomes sont présents dans la grande poêle, il faut donc plus d’énergie pour faire vibrer tous ces atomes plus rapidement. La capacité thermique de la petite poêle en fonte est déterminée en observant qu’il faut 18 150 J d’énergie pour augmenter la température de la poêle de 50,0 °C :

La plus grande poêle en fonte, bien que fabriquée dans la même matière, a besoin de 90 700 J d’énergie pour augmenter sa température de 50,0 °C. La plus grande poêle a une capacité thermique (proportionnellement) plus grande parce que la plus grande quantité de matière nécessite une quantité d’énergie (proportionnellement) plus grande pour produire le même changement de température :

La capacité calorifique spécifique (c) d’une substance, communément appelée “chaleur spécifique”, est la quantité de chaleur nécessaire pour élever la température d’un gramme d’une substance de 1 degré Celsius (ou 1 kelvin) :

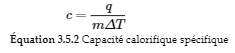
Notez la différence importante en unités entre C et c : la capacité thermique, C, est exprimée en énergie par changement de température, alors que la capacité thermique spécifique, c, est également exprimée en énergie par changement de température, mais cette fois par masse. En d’autres termes, la capacité calorifique spécifique va plus loin en tenant compte de la masse.

La capacité thermique spécifique dépend uniquement du type de substance qui absorbe ou libère la chaleur. C’est une propriété intensive – le type, mais pas la quantité, de la substance est tout ce qui compte. Par exemple, la petite poêle à frire en fonte a une masse de 808 g. La chaleur spécifique du fer (le matériau utilisé pour fabriquer la poêle) est donc :

La grande poêle à frire a une masse de 4040 g. En utilisant les données de cette poêle, nous pouvons également calculer la chaleur spécifique du fer :

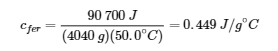
Bien que la grande casserole soit plus massive que la petite, comme elles sont toutes deux faites du même matériau, elles produisent toutes deux la même valeur de chaleur spécifique (pour le matériau de construction, le fer). Notez que la chaleur spécifique est mesurée en unités d’énergie par température par masse et qu’elle est une propriété intensive, étant dérivée d’un rapport entre deux propriétés extensives (chaleur et masse). La capacité thermique molaire, également une propriété intensive, est la capacité thermique par mole d’une substance particulière et a des unités de J/mol °C (figure 3.5.1).

Dans les applications de la vie réelle, nous utilisons généralement le C pour les applications à grande échelle comme les objets dont la masse exacte n’est pas importante et dont les différences de masse peuvent être constatées qualitativement (l’objet est plus grand, semble beaucoup plus lourd), ou lorsque nous travaillons avec des objets de taille différente et de même composition. La capacité thermique spécifique, c, s’applique à des applications à plus petite échelle comme les substances dont la masse devient un élément important à prendre en compte pour répondre à des exigences spécifiques (par exemple, déterminer la masse de NH₄NO₃ la plus appropriée à utiliser dans une banquise qui est pratique en termes de masse et qui fournit un changement de température qui est correct).

Figure 3.5.1. En raison de sa masse plus importante, une grande poêle à frire a une plus grande capacité calorifique qu’une petite poêle à frire. Comme elles sont faites du même matériau, les deux poêles à frire ont la même chaleur spécifique. (crédit : Mark Blaser)

L’eau liquide a une chaleur spécifique relativement élevée (environ 4,2 J/g °C) ; la plupart des métaux ont une chaleur spécifique beaucoup plus faible (généralement inférieure à 1 J/g °C). La chaleur spécifique d’une substance varie quelque peu en fonction de la température. Cependant, cette variation est généralement assez faible pour que nous considérions la chaleur spécifique comme constante sur la gamme de températures qui sera examinée dans ce chapitre. Les chaleurs spécifiques de certaines substances courantes sont énumérées dans le tableau ci-dessous.

Tableau 3.5.1 Chaleurs spécifiques des substances courantes à 25°C et 1 bar*

* Manuel de chimie et de physique du CRC 100e édition (en ligne) (éd. électronique). (2019). Boca Raton, Fla : CRC Press.

Si nous connaissons la masse d’une substance et sa chaleur spécifique, nous pouvons déterminer la quantité de chaleur, q, qui entre ou sort de la substance en mesurant le changement de température avant et après que la chaleur soit gagnée ou perdue :

Dans cette équation, c est la chaleur spécifique de la substance, m est sa masse, et ΔT (qui se lit “delta T”) est le changement de température, T_final – T_initial. Comme c et m sont tous deux des valeurs toujours positives, la seule variable qui détermine si la chaleur est absorbée ou libérée est la variation de température. Si une substance gagne de l’énergie thermique, sa température augmente, sa température finale est supérieure à sa température initiale, Tfinal – _Tinitial a une valeur positive, et la valeur de q est positive. Si une substance perd de l’énergie thermique, sa température diminue, la température finale est inférieure à la température initiale, Tfinal – _{Tinitial a une valeur} négative, et la valeur de q est négative. Si vous essayez de faire le calcul en utilisant l’équation q = mcΔT, vous verrez que ce raisonnement se vérifie :

Exemple 3.5.1 – Mesurer la chaleur

Un ballon contenant 8,0 × 10² g d’eau est chauffé, et la température de l’eau passe de 21 °C à 85 °C. Quelle quantité de chaleur l’eau a-t-elle absorbée ?

Solution

Pour répondre à cette question, il faut tenir compte de ces facteurs :

• la chaleur spécifique de la substance chauffée (dans ce cas, l’eau)
• la quantité de substance chauffée (dans ce cas, 8,0 × 10² g)
• l’ampleur du changement de température (dans ce cas, de 21 °C à 85 °C).

La chaleur spécifique de l’eau est de 4,184 J/g °C, donc pour chauffer 1 g d’eau de 1 °C, il faut 4,184 J. Nous notons que puisque 4,184 J est nécessaire pour chauffer 1 g d’eau de 1 °C, il en faudra 800 fois plus pour chauffer 8,0 × 10² g d’eau de 1 °C. Enfin, nous observons que puisqu’il faut 4,184 J pour chauffer 1 g d’eau de 1 °C, il nous en faudra 64 fois plus pour le chauffer de 64 °C (c’est-à-dire de 21 °C à 85 °C).

On peut résumer cela à l’aide de l’équation :

q = c × m × ΔT = c × m × (T_finale – T_initiale)

= (4,184 J/g^∘C) × (8,0 × 10² g) × (85 – 21)^∘C

= (4,184 J/g^∘C) × (8,0 × 10² g) × (64)^∘C

= 210000 J (= 2,1 × 10² kJ)

Comme la température a augmenté, l’eau a absorbé de la chaleur et q est positif.

Vérifiez votre apprentissage 3.5.1 – Mesurer la chaleur

Quelle quantité de chaleur, en joules, doit être ajoutée à une poêle en fer de 5,07 × 10⁴ J pour faire passer sa température de 25 °C à 250 °C ? La chaleur spécifique du fer est de 0,449 J/g °C.

Réponse

5.07 × 10⁴ J

Notez que la relation entre la chaleur, la chaleur spécifique, la masse et le changement de température peut être utilisée pour déterminer n’importe laquelle de ces quantités (et pas seulement la chaleur) si les trois autres sont connues ou peuvent être déduites.

Exemple 3.5.2 – Détermination d’autres quantités

Un morceau de métal inconnu pèse 348 g. Lorsque le morceau de métal absorbe 6,64 kJ de chaleur, sa température passe de 22,4 °C à 43,6 °C. Déterminez la chaleur spécifique de ce métal (qui pourrait fournir un indice sur son identité).

Solution

Comme on connaît la masse, la chaleur et la variation de température de ce métal, on peut déterminer sa chaleur spécifique grâce à cette relation :

q = c × m × ΔT = c × m × (T_finale – T_initiale)

Substituer les valeurs connues :

6640 J = c × (348 g) × (43.6 – 22.4)^∘C

Résoudre :

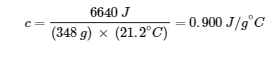
En comparant cette valeur avec les valeurs du tableau pour les chaleurs spécifiques des substances communes (à 25°C et 1 bar), cette valeur correspond à la chaleur spécifique de l’aluminium, ce qui suggère que le métal inconnu est l’aluminium.

Vérifiez votre apprentissage 3.5.2 – Détermination d’autres quantités

Un morceau de métal inconnu pèse 217 g. Lorsque le morceau de métal absorbe 1,43 kJ de chaleur, sa température passe de 24,5 °C à 39,1 °C. Déterminez la chaleur spécifique de ce métal, et prévoyez son identité.

Répondez

c = 0,451 J/g °C ; le métal est susceptible d’être du fer

Mesure du flux thermique – Calorimètres

Un calorimètre est un appareil utilisé pour mesurer la quantité de chaleur impliquée dans un processus chimique ou physique. Par exemple, lorsqu’une réaction exothermique se produit en solution dans un calorimètre, la chaleur produite par la réaction est absorbée par la solution, ce qui augmente sa température. Lorsqu’une réaction endothermique se produit, la chaleur nécessaire est absorbée par l’énergie thermique de la solution, ce qui diminue sa température (figure 3.5.2). Le changement de température, ainsi que la chaleur et la masse spécifiques de la solution, peuvent alors être utilisés pour calculer la quantité de chaleur impliquée dans les deux cas.

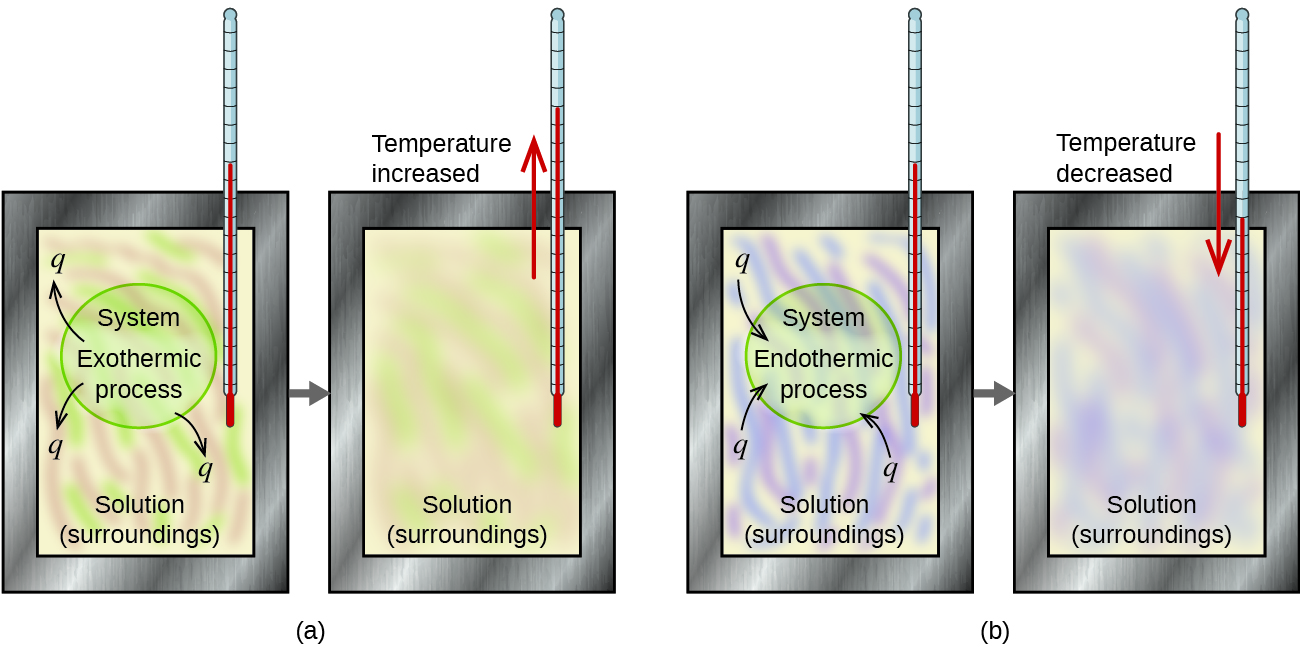
Figure 3.5.2. Dans une détermination calorimétrique, soit (a) un processus exothermique se produit et la chaleur, q, est négative, ce qui indique que l’énergie thermique est transférée du système à son environnement, soit (b) un processus endothermique se produit et la chaleur, q, est positive, ce qui indique que l’énergie thermique est transférée de l’environnement au système.

Les scientifiques utilisent des calorimètres bien isolés qui empêchent pratiquement tout transfert de chaleur entre le calorimètre et son environnement. Cela permet de déterminer avec précision la chaleur impliquée dans les processus chimiques, le contenu énergétique des aliments, etc.

Prenons un exemple simple qui illustre l’idée centrale de la calorimétrie. Supposons que nous ayons initialement une substance à haute température, comme un morceau de métal chaud (M), et une substance à basse température, comme de l’eau froide (W). Si nous plaçons le métal dans l’eau, la chaleur passera de M à W. La température de M diminuera, et la température de W augmentera jusqu’à ce que les deux substances aient la même température – lorsqu’elles atteindront l’équilibre thermique (figure 3.5.3). Si cela se produit dans un calorimètre, idéalement, tout ce transfert de chaleur se produit entre les deux substances, sans qu’il y ait de gain ou de perte de chaleur ni par le calorimètre ni par son environnement. Dans ces circonstances idéales, la variation nette de chaleur est nulle :

q_{substance M} + q_{substance W} = 0

Cette relation peut être réarrangée pour montrer que la chaleur gagnée par la substance M est égale à la chaleur perdue par la substance W :

q_{substance M} = – q_{substance W}

Rappelons la première loi de la thermodynamique : l’énergie n’est ni gagnée ni détruite, mais seulement transférée. Pour les problèmes de calorimétrie, gardez à l’esprit que la chaleur ne circule que dans une seule direction – toujours du chaud vers le froid. Ainsi, alors qu’une substance émet de la chaleur, l’autre substance va absorber cette chaleur. L’ampleur de la chaleur (changement) est donc la même pour les deux substances, et le signe négatif indique simplement que q_{substance M} et q_{substance W} sont opposées dans la direction du flux de chaleur (gain ou perte), mais n’indique pas le signe arithmétique de l’une ou l’autre valeur de q (qui est déterminé par le fait que la matière en question gagne ou perd de la chaleur, par définition). Dans la situation spécifique décrite, qsubstance _M est une valeur négative et qsubstance _{W est} positive, puisque la chaleur est transférée de M à W.

Figure 3.5.3. Dans un processus de calorimétrie simple, (a) la chaleur, q, est transférée du métal chaud, M, à l’eau froide, W, jusqu’à ce que (b) les deux soient à la même température.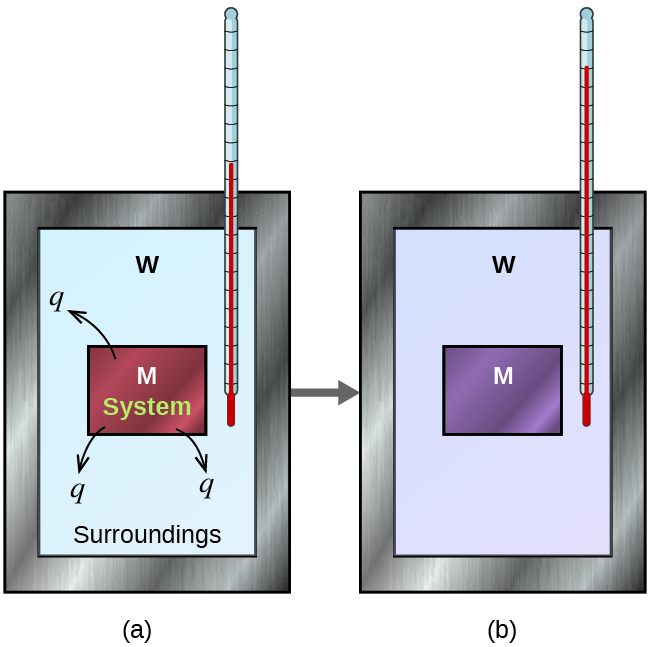

Ici, nous parlerons de deux types de calorimètres : les calorimètres “tasse à café” et les calorimètres “bombe”.

Calorimétrie “Coffee-Cup” (ou pression constante)

Les étudiants en chimie générale utilisent souvent des calorimètres simples construits à partir de gobelets en polystyrène (figure 3.5.4). Ces calorimètres “tasse à café” faciles à utiliser fonctionnent à une pression constante pour permettre un plus grand échange de chaleur avec l’environnement extérieur et donc produire des valeurs énergétiques moins précises. En termes d’applications réelles, ces calorimètres sont plus appropriés pour les processus endothermiques et légèrement exothermiques. Les réactions hautement exothermiques, telles que les réactions de combustion, sont généralement réalisées à l’aide de calorimètres à bombe (dont nous parlerons plus loin).

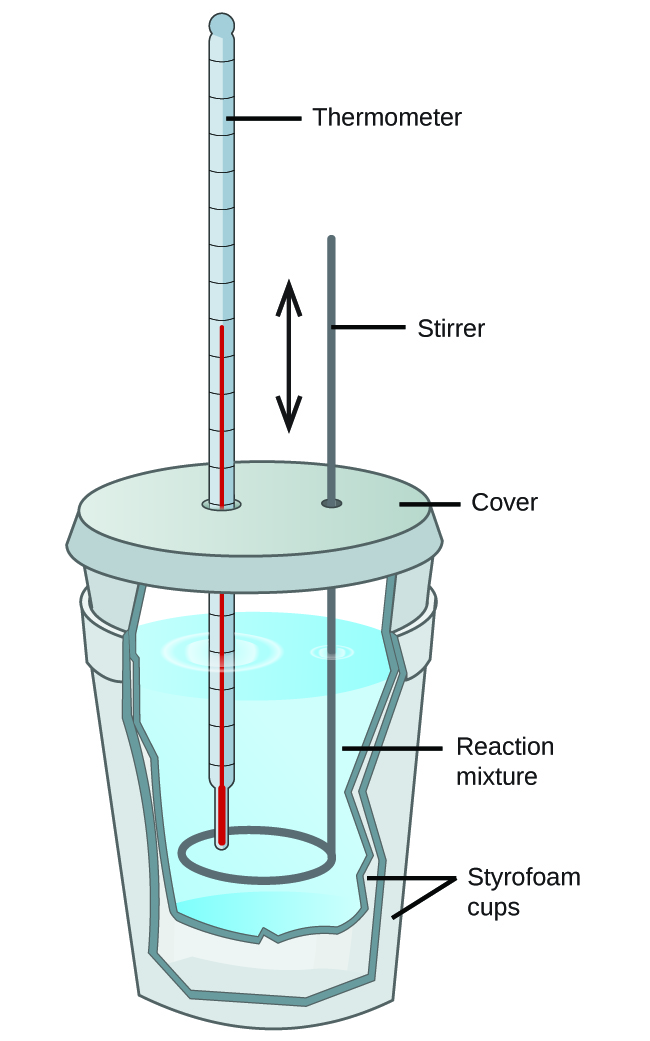
Figure 3.5.4. Un simple calorimètre peut être construit à partir de deux coupelles en polystyrène. Un thermomètre et un agitateur traversent le couvercle et pénètrent dans le mélange réactionnel.

Des calorimètres à solution commerciale sont également disponibles. Les calorimètres relativement peu coûteux sont souvent constitués de deux coupelles à paroi mince qui sont emboîtées de manière à minimiser le contact thermique pendant l’utilisation, ainsi que d’un couvercle isolé, d’un agitateur à main et d’un simple thermomètre. Les calorimètres plus coûteux utilisés dans l’industrie et la recherche ont généralement une cuve de réaction bien isolée et entièrement fermée, un mécanisme d’agitation motorisé et un capteur de température plus précis (figure 3.5.5).

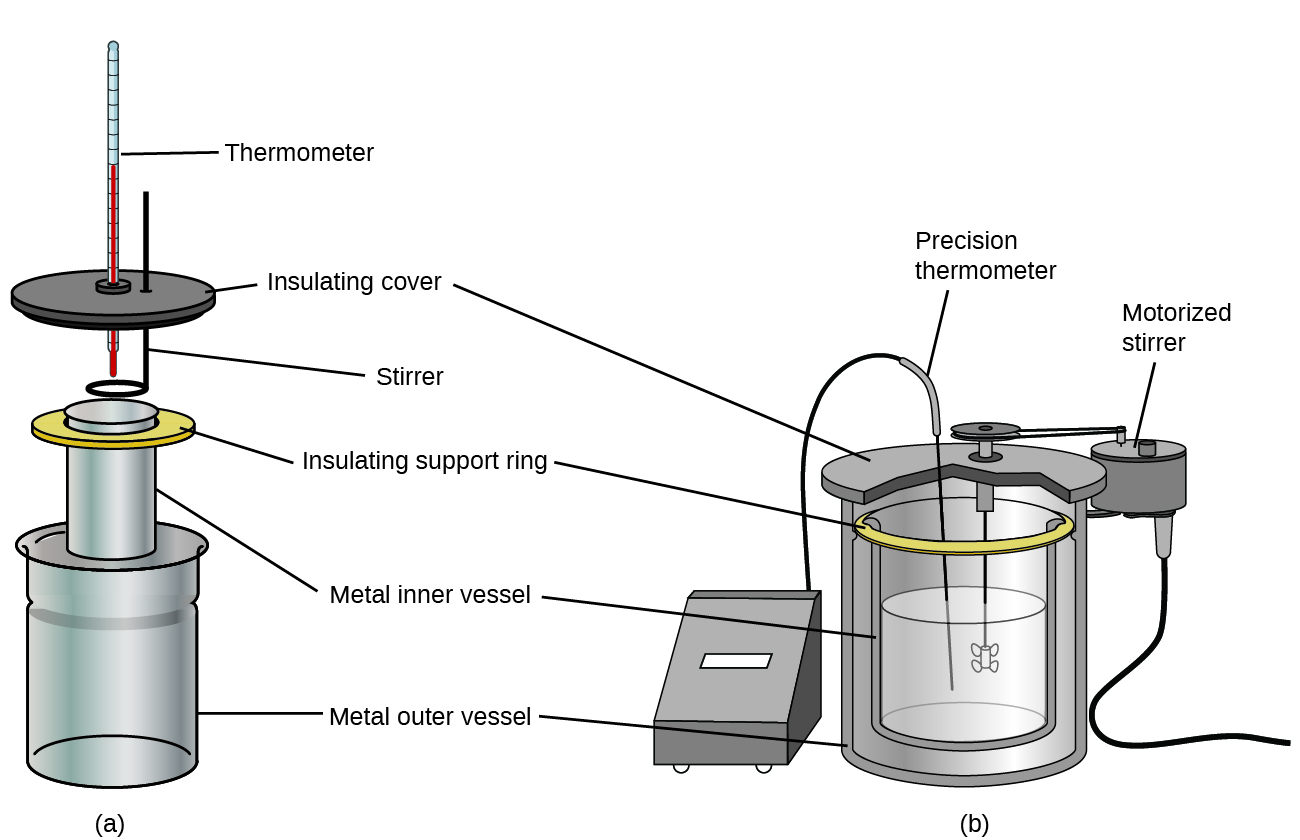
Figure 3.5.5. Les calorimètres à solution commerciale vont de (a) modèles simples et peu coûteux pour les étudiants à (b) modèles plus précis et coûteux pour l’industrie et la recherche.

Exemple 3.5.3 – Transfert de chaleur entre des substances à des températures différentes

Un morceau de barre d’armature de 360,0 g (une tige d’acier utilisée pour renforcer le béton) est plongé dans 425 ml d’eau à 24,0 °C. La température finale de l’eau a été mesurée à 42,7 °C. Calculer la température initiale du morceau de barre d’armature. Supposons que la chaleur spécifique de l’acier soit approximativement la même que celle du fer (voir le tableau 3.5.1) des chaleurs spécifiques des substances communes), et que tout le transfert de chaleur se fasse entre la barre d’armature et l’eau (il n’y a pas d’échange de chaleur avec l’environnement).

Solution

La température de l’eau passe de 24,0°C à 42,7°C, l’eau absorbe donc de la chaleur. Cette chaleur provient du morceau de barre d’armature, qui était initialement à une température plus élevée. En supposant que tout le transfert de chaleur s’est fait entre la barre d’armature et l’eau, sans “perte” de chaleur vers l’environnement extérieur, alors la chaleur dégagée par la barre d’armature = -chaleur absorbée par l’eau, ou :

q_{barre d’armature} = – q_eau

Comme nous savons comment la chaleur est liée à d’autres quantités mesurables, nous l’avons fait :

(c × m × ΔT)_{barre d’armature} = – (c × m × ΔT)_eau

En laissant f = final et i = initial, sous forme élargie, cela devient :

c_{barre d’armature} × m_{barre d’armature} × (T_{f,barre d’armature} -T_{i,barre d’armature}) = – c_eau × m_eau × (T_f,eau – T_i,eau)

La densité de l’eau est de 1,0 g/mL, donc 425 ml d’eau = 425 g. Notant que la température finale de l’armature et de l’eau est de 42,7°C, on remplace les valeurs connues par des rendements :

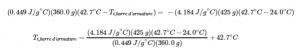
La résolution de ce problème donne T_{i, barre d’armature =} 248°C, donc la température initiale de la barre d’armature était de 248°C.

Vérifiez votre apprentissage 3.5.3 – Transfert de chaleur entre des substances à des températures différentes

On fait tomber un morceau de cuivre de 248 g dans 390 ml d’eau à 22,6 °C. La température finale de l’eau a été mesurée à 39,9 °C. Calculez la température initiale du morceau de cuivre. Supposez que tout le transfert de chaleur se fait entre le cuivre et l’eau.

Réponse

La température initiale du cuivre était de 335,6°C.

Vérifiez votre apprentissage 3.5.4 – Transfert de chaleur entre des substances à des températures différentes

Un morceau de cuivre de 248 g initialement à 314 °C est plongé dans 390 ml d’eau initialement à 22,6 °C. En supposant que tout le transfert de chaleur s’effectue entre le cuivre et l’eau, calculer la température finale.

Réponse

La température finale (atteinte par le cuivre et l’eau) est de 38,7 °C.

Cette méthode peut également être utilisée pour déterminer d’autres quantités, comme la chaleur spécifique d’un métal inconnu.

Exemple 3.5.4 – Identifier un métal en mesurant une chaleur spécifique

Un morceau de métal de 59,7 g qui avait été submergé dans de l’eau bouillante a été rapidement transféré dans 60,0 ml d’eau initialement à 22,0 °C. La température finale est de 28,5 °C. Utilisez ces données pour déterminer la chaleur spécifique du métal. Utilisez ce résultat pour identifier le métal.

Solution

En supposant un transfert de chaleur parfait, la chaleur dégagée par le métal = -chaleur absorbée par l’eau, ou :

q_métal = – q_eau

Sous une forme élargie, c’est :

c_métal× m_métal × (T_f,métal – T_i,métal) = – c_eau × m_eau × (T_f,eau – T_i,eau)

Notant que depuis que le métal a été submergé dans de l’eau bouillante, sa température initiale était de 100,0°C ; et que pour l’eau, 60,0 ml = 60,0 g ; nous l’avons fait :

(c_métal)(59,7 g)(28,5^∘C – 100^∘C) = – (4,18 J/g^∘C)(60,0 g)(28,5^∘C – 22,0^∘C)

En comparant ces valeurs avec celles du tableau (tableau 3.5.1) des chaleurs spécifiques des substances courantes, notre chaleur spécifique expérimentale est la plus proche de la valeur pour le cuivre (0,39 J/g °C), de sorte que nous identifions le métal comme étant probablement du cuivre.

Vérifiez votre apprentissage 3.5.5 – Identifier un métal en mesurant une chaleur spécifique

Un morceau de 92,9 g d’un métal argent/gris est chauffé à 178,0 °C, puis rapidement transféré dans 75,0 ml d’eau, initialement à 24,0 °C. Au bout de 5 minutes, le métal et l’eau ont atteint la même température : 29,7°C. Déterminez la chaleur spécifique et l’identité du métal. (Remarque : vous devriez constater que la chaleur spécifique est proche de celle de deux métaux différents. Expliquez comment vous pouvez déterminer avec certitude l’identité du métal).

Réponse

c_métal = 0,13 J/g °C

Cette chaleur spécifique est proche de celle de l’or ou du plomb. Il serait difficile de déterminer quel métal il s’agit en se basant uniquement sur les valeurs numériques. Cependant, l’observation que le métal est argent/gris en plus de la valeur de la chaleur spécifique indique que le métal est du plomb.

Lorsque nous utilisons la calorimétrie pour déterminer la chaleur impliquée dans une réaction chimique, les mêmes principes dont nous avons parlé s’appliquent. La quantité de chaleur absorbée par le calorimètre est souvent suffisamment faible pour que nous puissions la négliger (mais pas pour des mesures très précises, comme nous le verrons plus loin), et le calorimètre minimise l’échange d’énergie avec l’environnement extérieur. Comme l’énergie n’est ni créée ni détruite lors d’une réaction chimique, il n’y a pas de changement global d’énergie pendant la réaction. La chaleur produite ou consommée dans la réaction (le “système”), q_réaction, plus la chaleur absorbée ou perdue par la solution (l'”environnement”), q_solution, doivent s’additionner pour donner zéro :

q_réaction + q_solution = 0

Cela signifie que la quantité de chaleur produite ou consommée dans la réaction est égale à la quantité de chaleur absorbée ou perdue par la solution :

q_réaction = – q_solution

Ce concept est au cœur de tous les problèmes et calculs de calorimétrie. Si la quantité de chaleur absorbée par un calorimètre est trop importante pour être négligée ou si nous voulons des résultats plus précis, nous devons alors prendre en compte la chaleur absorbée à la fois par la solution et par le calorimètre.

Exemple 3.5.5 – Chaleur produite par une réaction exothermique

Lorsque 50,0 ml de HCl (aq) 1,00 M et 50,0 ml de NaOH (aq) 1,00 M, tous deux à 22,0°C, sont ajoutés à un calorimètre à tasse de café, la température du mélange atteint un maximum de 28,9°C. Quelle est la quantité approximative de chaleur produite par cette réaction ?

HCl (aq) + NaOH (aq)  →  NaCl (aq) + H₂O (l)

Solution

Pour visualiser ce qui se passe, imaginez que vous puissiez combiner les deux solutions si rapidement qu’aucune réaction ne se produise pendant qu’elles se mélangent ; puis après le mélange, la réaction se produit. Au moment du mélange, vous avez 100,0 ml d’un mélange de HCl et de NaOH à 22,0°C, et ce sera donc cette solution entière de 100,0 ml qui absorbera la chaleur dégagée par la réaction. Le HCl et le NaOH réagissent alors jusqu’à ce que la température de la solution atteigne 28,9°C.

La chaleur dégagée par la réaction est égale à celle absorbée par la solution. Par conséquent, la chaleur dégagée par la réaction est égale à celle absorbée par la solution :

q_réaction = – q_solution

(Il est important de se rappeler que cette relation ne tient que si le calorimètre n’absorbe aucune chaleur de la réaction, et qu’il n’y a pas d’échange de chaleur entre le calorimètre et l’environnement extérieur).

Ensuite, nous savons que la chaleur absorbée par la solution dépend de sa chaleur spécifique, de sa masse et du changement de température :

q_solution = (c × m × ΔT)_solution

Pour procéder à ce calcul, nous devons faire quelques hypothèses ou approximations plus raisonnables. Comme la solution est aqueuse, nous pouvons procéder comme s’il s’agissait d’eau en termes de valeurs de chaleur spécifique et de masse. La densité de l’eau est d’environ 1,0 g/mL, donc 100,0 ml ont une masse d’environ 1,0 × 10² g (deux chiffres significatifs). La chaleur spécifique de l’eau est d’environ 4,184 J/g °C, nous utilisons donc cette valeur pour la chaleur spécifique de la solution. En substituant ces valeurs, on obtient :

q_solution = (4.,84 J/g∘C)(1,0 × 10² g)(28,9^∘C – 22,0^∘C) = 2.9 × 10³ J

Enfin, puisque nous essayons de trouver la chaleur de la réaction, nous l’avons fait :

q_réaction = – q_solution = – 2.9 × 10³ J

Le signe négatif indique que la réaction est exothermique. Elle produit 2,9 kJ de chaleur.

Vérifiez votre apprentissage 3.5.6 – Chaleur produite par une réaction exothermique

Lorsque 100 ml de NaCl(aq) 0,200 M et 100 ml de AgNO₃(aq) 0,200 M, tous deux à 21,9°C, sont mélangés dans un calorimètre à tasse à café, la température augmente à 23,5°C au fur et à mesure que de l’AgCl solide se forme. Quelle est la quantité de chaleur produite par cette réaction de précipitation ? Quelles hypothèses avez-vous faites pour déterminer votre valeur ?

Réponse

1,34 × 10³ J ; supposons qu’aucune chaleur n’est absorbée par le calorimètre, qu’il n’y a pas d’échange de chaleur entre le calorimètre et son environnement, et que la chaleur et la masse spécifiques de la solution sont les mêmes que pour l’eau

Comme nous l’avons vu dans l’exemple précédent, nous avons supposé que la capacité thermique spécifique du mélange de solution de HCl(aq) et de NaOH(aq) était égale à celle de l’eau. Par conséquent, dans les problèmes de calorimétrie (sauf mention contraire), vous pouvez fixer la valeur de c pour les solutions à 4,184 J/g °C si l’hypothèse est raisonnable (par exemple, les réactifs utilisés sont tous des solutions aqueuses).

Exemple 3.5.6 – Flux de chaleur dans une banquise instantanée

Lorsque le nitrate d’ammonium solide se dissout dans l’eau, la solution devient froide. C’est la base d’un “instant ice pack” (figure 3.5.6). Lorsque 3,21 g de NH₄NO₃ solide se dissout dans 50,0 g d’eau à 24,9°C dans un calorimètre, la température descend à 20,3°C.

Calculer la valeur de q pour cette réaction et expliquer la signification de son signe arithmétique. Indiquez les hypothèses que vous avez faites.

Figure 3.5.6. Une poche froide instantanée se compose d’un sac contenant du nitrate d’ammonium solide et d’un second sac d’eau. Lorsque le sac d’eau est brisé, la poche devient froide car la dissolution du nitrate d’ammonium est un processus endothermique qui retire l’énergie thermique de l’eau. La poche froide élimine alors l’énergie thermique de votre corps.

Solution

Nous supposons que le calorimètre empêche le transfert de chaleur entre la solution et son environnement externe (y compris le calorimètre lui-même), auquel cas :

q_rxn = – q_soln

avec “rxn” et “soln” utilisés comme abréviations pour “réaction” et “solution”, respectivement.

Note : Nous disons ici que c’est la solution qui perd de la chaleur, et non le solvant. Dans vos calculs, lorsque vous considérez la valeur de la masse, m, vous devez utiliser la masse de la solution, et non le solvant ! Lorsque la réaction commence, la quantité de sel est déjà dissoute et ajoutée à la quantité d’eau présente, donc la solution est présente et sera celle qui émet de la chaleur. Selon la loi de conservation de la masse, la masse totale de la solution doit être la somme des masses pour le sel et l’eau, c’est donc cette masse totale de solution qui perd de la chaleur.

En supposant également que la chaleur spécifique de la solution est la même que celle de l’eau, nous avons :

q_rxn = – q_soln = – (c × m × ΔT)_soln

= – [(4,184 J/g^∘C) × (53,2 g) × (20,3^∘C – 24,9^∘C)]

= – [(4,184 J/g^∘C) × (53,2 g) × (- 4,6^∘C)]

+ 1,0 × 103 J = + 1,0 kJ

Le signe positif pour q indique que la dissolution est un processus endothermique.

Vérifiez votre apprentissage 3.5.7 – Flux de chaleur dans une banquise instantanée

Lorsqu’un échantillon de 3,00 g de KCl a été ajouté à 3,00 × 10² g d’eau dans un calorimètre à tasse de café, la température a diminué de 1,05 °C. Quelle est la quantité de chaleur impliquée dans la dissolution du KCl ? Quelles hypothèses avez-vous faites ?

Réponse

1,33 kJ ; supposons que le calorimètre empêche le transfert de chaleur entre la solution et son environnement externe (y compris le calorimètre lui-même) et que la chaleur spécifique de la solution est la même que celle de l’eau

Calorimétrie de la bombe (ou du volume constant)

Les calorimètres pour tasses de café décrits précédemment sont conçus pour fonctionner à une pression (atmosphérique) constante et sont pratiques pour mesurer le flux thermique accompagnant les processus qui se produisent en solution. Un autre type de calorimètre qui fonctionne à volume constant, le calorimètre à bombe, est utilisé pour mesurer l’énergie produite par des réactions très exothermiques qui produisent de grandes quantités de chaleur et de produits gazeux, comme les réactions de combustion. Ce type de calorimètre est constitué d’un solide conteneur en acier (la “bombe”) qui contient les réactifs et est lui-même immergé dans l’eau (figure 3.5.8). L’échantillon est placé dans la bombe, qui est ensuite remplie d’oxygène à haute pression. Une petite étincelle électrique est utilisée pour enflammer l’échantillon. L’énergie produite par la réaction est absorbée par la bombe en acier et l’eau environnante. L’augmentation de la température est mesurée et, avec la capacité thermique connue du calorimètre, est utilisée pour calculer l’énergie produite par la réaction. Les calorimètres à bombe doivent être calibrés pour déterminer la capacité thermique du calorimètre et garantir des résultats précis. Le calibrage est effectué à l’aide d’une réaction dont le q est connu, comme une quantité mesurée d’acide benzoïque enflammée par une étincelle provenant d’un fil fusible en nickel qui est pesée avant et après la réaction. Le changement de température produit par la réaction connue est utilisé pour déterminer la capacité thermique du calorimètre. L’étalonnage est généralement effectué à chaque fois avant que le calorimètre ne soit utilisé pour recueillir des données de recherche.

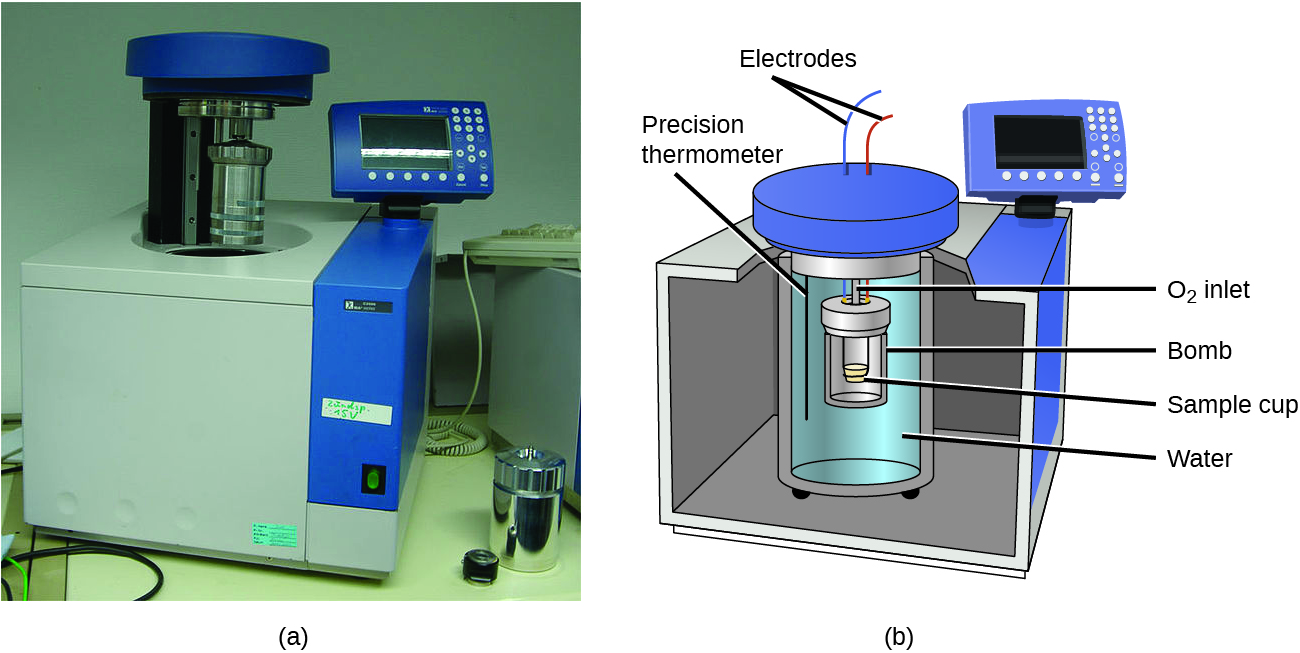Figure 3.5.8. (a) Un calorimètre à bombe est utilisé pour mesurer la chaleur produite par des réactions impliquant des réactifs ou des produits gazeux, comme la combustion. (b) Les réactifs sont contenus dans la “bombe” étanche aux gaz, qui est submergée dans l’eau et entourée de matériaux isolants. (crédit: modification du travail par “Harbor1″/Wikimedia commons)

Exemple 3.5.7 – Calorimétrie à bombe

Lorsque 3,12 g de glucose, _C6H12O6, sont brûlés dans un calorimètre à bombe, la température du calorimètre passe de 23,8°C à 35,6°C. Le calorimètre contient 775 g d’eau, et la bombe elle-même a une capacité calorifique de 893 J/°C.

(a) Quelle quantité de chaleur a été produite par la combustion de l’échantillon de glucose ?

(b) La décomposition métabolique du glucose est assez similaire à sa combustion – elle nécessite de l’oxygène (O₂) pour son oxydation, sauf que l’énergie récoltée du glucose est principalement utilisée pour effectuer des processus cellulaires. En supposant que la même quantité d’énergie provenant de la partie (a) soit exploitée en consommant le même échantillon de glucose et en le métabolisant, à quelle quantité de calories nutritionnelles (Cal) cela correspondrait-il ?

Solution

(a) La combustion produit de la chaleur qui est principalement absorbée par l’eau et la bombe. (Les quantités de chaleur absorbées par les produits de réaction et l’excès d’oxygène n’ayant pas réagi sont relativement faibles et leur traitement dépasse le cadre de ce texte. Nous les négligerons dans nos calculs).

La chaleur produite par la réaction est absorbée par l’eau et la bombe :

q_rxn = – (q_eau + q_bombe) = – {[m_eau × c_eau × (T_f – T_i)] + [C_cal × (T_f – T_i)]}

= – [(4,184 J/g^∘C) × (775 g) × (35,6^∘C – 23,8^∘C) + 893 J/^∘C × (35,6^∘C –                        23,8^∘C)]

= – (38300 J + 10500 J)

= – 48800 J = – 48,8 kJ

Cette réaction a libéré 48,7 kJ de chaleur lorsque 3,12 g de glucose ont été brûlés.

(b) L’énergie produite, exprimée en kilojoules, peut facilement être exprimée en calories et en outre en Calories en effectuant une conversion d’unité :

Ainsi, une personne consommant 3,12 g de glucose obtiendrait environ 11,6 calories.

Vérifiez votre apprentissage 3.5.8 – Calorimétrie à bombe

Lorsque 0,963 g de benzène, _C6H6, est brûlé dans un calorimètre à bombe, la température du calorimètre augmente de 8,39°C. La bombe a une capacité calorifique de 784 J/°C et est immergée dans 925 ml d’eau. Quelle quantité de chaleur a été produite par la combustion de l’échantillon de glucose ?

Réponse

39,0 kJ

Questions

★ Questions

1. Une bouteille d’eau de 500 ml à température ambiante et une bouteille d’eau de 2 litres à la même température ont été placées dans un réfrigérateur. Après 30 minutes, la bouteille de 500 ml d’eau avait refroidi à la température du réfrigérateur. Une heure plus tard, les 2 litres d’eau avaient refroidi à la même température. Lorsqu’on leur a demandé quel échantillon d’eau avait perdu le plus de chaleur, quatre élèves ont donné les réponses suivantes,

         a. Les deux bouteilles ont perdu la même quantité de chaleur parce qu’elles                 ont commencé à la même température et se sont terminées à la même                         température.

         b. La bouteille d’eau de 2 litres a perdu plus de chaleur parce qu’il y avait plus              d’eau.

         c. La bouteille d’eau de 500 ml a perdu plus de chaleur car elle a refroidi plus                rapidement.

         d. Il n’est pas possible de le dire car nous ne connaissons pas la température               initiale et la température finale de l’eau.

Indiquez laquelle de ces réponses est correcte et décrivez l’erreur dans chacune des autres réponses.

   2. La quantité de chaleur mesurée dans une réaction exothermique serait-elle plus    importante, moins importante ou resterait-elle la même si nous utilisions un              calorimètre moins isolant qu’un calorimètre à tasse de café ? Expliquez votre              réponse.

   3. La quantité de chaleur absorbée par la dissolution dans l’exemple 6. (flux de          chaleur dans une banquise instantanée) semblerait plus importante, moindre ou        resterait la même si l’expérimentateur utilisait un calorimètre moins isolant qu’un      calorimètre à tasse de café ? Expliquez votre réponse.

★★ Questions

   4. Combien de millilitres d’eau (volume) à 23 °C avec une densité de 1,00 g/mL           doivent être mélangés à 180 ml de café à 95 °C pour que la combinaison obtenue     ait une température de 60 °C ? Supposons que le café et l’eau ont la même                 densité et la même chaleur spécifique.

   5. Dans quelle mesure la température d’une tasse (180 g) de café à 95 °C sera-t-       elle réduite lorsqu’une cuillère en argent de 45 g (chaleur spécifique de 0,24 J/g           °C) à 25 °C est placée dans le café et que les deux atteignent la même                           température ? Supposons que le café ait la même densité et la même chaleur             spécifique que l’eau.

   6. Lorsque 50,0 g de NaCl (aq) 0,200 M à 24,1 °C sont ajoutés à 100,0 g                         d’AgNO₃ (aq) 0,100 M à 24,1 °C dans un calorimètre, la température augmente à         25,2 °C au fur et à mesure de la formation d’AgCl (s). En supposant que la                   chaleur spécifique de la solution et des produits est de 4,20 J/g °C, calculer la               quantité approximative de chaleur en joules produite.

   7. L’ajout de 3,15 g de Ba(OH)_2-8H₂O à une solution de 1,52 g de NH₄SCN dans 100     g d’eau dans un calorimètre a fait chuter la température de 3,1 °C. En supposant         que la chaleur spécifique de la solution et des produits est de 4,20 J/g °C, calculer       la quantité approximative de chaleur absorbée par la réaction (en kilojoules), qui       peut être représentée par l’équation suivante :

Ba(OH)₂ ・ 8H₂O (s) + 2 NH₄SCN (aq)  →  Ba(SCN)₂ (aq) + 2 NH₃ (aq) + 10 H₂O (l)

   8. Lorsque 1,0 g de fructose, C₆H₁₂O₆ (s), un sucre que l’on trouve couramment           dans les fruits, est brûlé dans de l’oxygène dans un calorimètre à bombe, la                 température du calorimètre augmente de 1,58 °C. Si la capacité calorifique du             calorimètre et de son contenu est de 9,90 kJ/°C, quel est le q de cette combustion     (en kilojoules) ?

   9. Lorsqu’un échantillon de 0,740 g de trinitrotoluène (TNT), C₇H₅N₂O₆, est brûlé       dans un calorimètre à bombe, la température passe de 23,4 °C à 26,9 °C. La                 capacité calorifique du calorimètre est de 534 J/°C, et il contient 675 ml d’eau.             Quelle quantité de chaleur a été produite par la combustion de l’échantillon de           TNT (en kilojoules) ?

   10. La quantité de graisse recommandée pour une personne ayant un régime             alimentaire quotidien de 2000 calories est de 65 g. Quel pourcentage des calories     de ce régime serait fourni par cette quantité de graisse si le nombre moyen de           calories pour la graisse est de 9,1 calories/g ?

   11. Une cuillère à café de saccharose (sucre commun) contient 16 Calories (16 kcal).     Quelle est la masse d’une cuillère à café de saccharose (en grammes) si le nombre      moyen de Calories pour les glucides est de 4,1 Calories/g ?

   12. Une pinte de crème glacée de qualité supérieure peut contenir 1100 Calories.         Quelle masse de graisse, en grammes et en livres, doit être produite dans le corps     pour stocker 1,1 × 10³ Calories supplémentaires si le nombre moyen de Calories            pour la graisse est de 9,1 Calories/g ?

   13. Quelle est la source d’énergie la moins chère en kilojoules par dollar : une boîte     de céréales pour petit déjeuner qui pèse 32 onces et coûte 4,23 dollars, ou un litre     d’isooctane (densité, 0,6919 g/mL) qui coûte 0,45 dollar ? Comparez la valeur               nutritionnelle de la céréale avec la chaleur produite par la combustion de                     l’isooctane dans des conditions normales. Une portion de 1,0 once de céréales             fournit 130 calories.

Réponses

1. L’étudiant 2 est correct. L’erreur dans la réponse du premier élève est d’avoir ignoré la masse d’eau. Pour le troisième élève, la réponse s’oppose à la question posée. Il a dû déclarer que la bouteille de 2 litres mettait plus de temps à atteindre la température du réfrigérateur et qu’elle perdait donc plus de chaleur. L’erreur dans la réponse du quatrième étudiant consiste à ignorer que le changement de température des deux bouteilles d’eau est le même et que les températures initiale et finale ne sont pas nécessaires.
2. Plus faible ; dans un isolant plus pauvre, une plus grande partie de la chaleur produite par la réaction s’échappera, ce qui semblerait être une valeur plus faible pour q.
3. Plus grande, puisque la prise en compte de la capacité thermique du calorimètre compensera l’énergie thermique transférée à la solution par le calorimètre ; cette approche inclut le calorimètre lui-même, ainsi que la solution, comme “environnement” : q_rxn = -(q_solution + qc_alorimètre) ; puisque la qsolution et le qcalorimètre sont tous deux négatifs, l’inclusion de ce dernier terme (qrxn) donnera une valeur plus grande pour la chaleur de la dissolution
4. 170,27 ml
5. La température du café va baisser d’un degré.
6. 693 J
7. 1,4 kJ
8. 15,64 kJ
9. 11,7 kJ
10. 30%
11. 3.90 g
12. 120,87 g, 0,055 lbs
13. En achetant un dollar d’isooctane, vous obtiendrez 7,349 x 10⁴ kJ. Un dollar de céréales ne fournirait que 4,12 kJ d’énergie. Par conséquent, avec un dollar, il est préférable d’investir dans l’isooctane pour obtenir plus d’énergie.