3.4 – Enthalpie

Qu’est-ce que l’enthalpie ?

Les chimistes utilisent généralement une propriété appelée enthalpie (H) pour décrire la thermodynamique des processus chimiques et physiques. L’enthalpie est définie comme la somme de l’énergie interne d’un système (U) et le produit mathématique de sa pression (P) et de son volume (V) :

H = U + PV

Équation 3.4.1 Enthalpie

Comme elle est dérivée de trois fonctions d’état (U, P et V), l’enthalpie est également une fonction d’état. Les valeurs d’enthalpie de substances spécifiques ne peuvent pas être mesurées directement ; seules les variations d’enthalpie de processus chimiques ou physiques peuvent être déterminées. Pour les processus qui se déroulent à pression constante (une condition commune à de nombreux changements chimiques et physiques), le changement d'enthalpie (ΔH) est :

ΔH = ΔU + PΔV

Équation 3.4.2 Changement d’enthalpie

Lorsque la pression est constante, le produit mathématique PΔV représente le travail (w), à savoir l’expansion ou le travail pression-volume comme indiqué. En se basant sur leurs définitions, les signes arithmétiques de ΔV et w seront toujours opposés :

PΔV = -w

Équation 3.4.3 Travail

La substitution de cette équation et de la définition de l’énergie interne dans l’équation de changement d’enthalpie donne:

ΔH = ΔU + PΔV

ΔH = (q_P + w) – w

ΔH = q_P

Équation 3.4.4 Changement d’enthalpie substituée

où q_P est la chaleur de réaction dans des conditions de pression constante. Ainsi, l’enthalpie est définie comme la quantité de chaleur transférée dans des conditions de pression constante.

Ainsi, si un processus chimique ou physique est réalisé à pression constante et que le seul travail effectué est causé par une expansion ou une contraction, alors le flux thermique (q_P) et le changement d’enthalpie (ΔH) du processus sont égaux.

La chaleur dégagée lorsque vous utilisez un bec Bunsen est égale au changement d’enthalpie de la réaction de combustion du méthane qui a lieu puisqu’elle se produit à la pression essentiellement constante de l’atmosphère. D’autre part, la chaleur produite par une réaction mesurée dans un calorimètre à bombe ([lien]) n’est pas égale à ΔH car le récipient métallique fermé et à volume constant empêche le travail d’expansion de se produire. Les chimistes réalisent généralement leurs expériences dans des conditions atmosphériques normales, à une pression externe constante avec q = ΔH, ce qui fait de l’enthalpie le choix le plus pratique pour déterminer la chaleur.

Comparaison entreΔH etΔU

Si l’on connaît ΔH pour une réaction, on peut utiliser la variation de l’enthalpie du système pour calculer sa variation d’énergie interne :

ΔH = ΔU + PΔV

Lorsqu’une réaction n’implique pas de gaz (c’est-à-dire qu’elle n’implique que des solides, des liquides, des solutions liquides ou toute combinaison de ceux-ci, le volume ne change pas sensiblement (ΔV ≈ 0). Dans ces conditions, nous pouvons simplifier l’équation ci-dessus où PΔV s’annule :

Réactions sans gaz  →  ΔH ≈ ΔU

Toutefois, lorsqu’une réaction implique des gaz, les valeurs de ΔH et ΔU peuvent être très différentes. Nous pouvons calculer ΔU à partir de la valeur mesurée de ΔH en modifiant le côté droit de l’équation, PΔV, avec la loi idéale des gaz, PV = nRT. P et T restent constants, nous reconnaissons donc que

PΔV = (Δn_gas)RT

Où

Δn_gaz = n_produits – n_réactifs

Nous pouvons réécrire l’équation du changement d’enthalpie comme suit :

Réaction avec gaz  →  ΔH = ΔU + Δn_gazRT

Où

Δn_gaz = n_produits – n_réactifs

Cette équation s’applique si Δn_gaz ≠ 0. Toutefois, si Δn_gaz = 0:

ΔH = ΔU

Équation 3.4.5 Relation du changement d’enthalpie et du changement de l’énergie interne

Changements d’Enthalpie dans les Réactions

Les conventions suivantes s’appliquent lorsque nous utilisons ΔH :

Les chimistes utilisent une équation thermochimique pour représenter les changements à la fois dans la matière et dans l’énergie. Dans une équation thermochimique, le changement d’enthalpie d’une réaction est représenté par une valeur ΔH qui suit l’équation de la réaction. Cette valeur ΔH indique la quantité de chaleur associée à la réaction impliquant le nombre de moles de réactifs et de produits comme indiqué dans l’équation chimique. Prenons par exemple cette équation :

H₂ (g) + 1/2 O₂ (g)  →  H₂O (l)      ΔH = – 286 kJ

Cette équation indique que lorsqu’une mole d’hydrogène gazeux et 1/2 des moles d’oxygène gazeux à une certaine température et pression se transforment en 1 mole d’eau liquide à la même température et pression, 286 kJ de chaleur sont libérés dans l’environnement. Si les coefficients de l’équation chimique sont multipliés par un facteur quelconque, le changement d’enthalpie doit être multiplié par ce même facteur (ΔH est une propriété étendue) :

(Montants multipliés par deux)

2 H₂ (g) + O₂ (g)  →  2 H₂O (l)     ΔH = 2 × (- 286 kJ) = – 572 kJ

(Montants multipliés par deux)

Le changement d’enthalpie d’une réaction dépend de l’état physique des réactifs et des produits de la réaction (que nous ayons des gaz, des liquides, des solides ou des solutions aqueuses), il faut donc les montrer. Par exemple, lorsque 1 mole d’hydrogène gazeux et 1/2 mole d’oxygène gazeux se transforme en 1 mole d’eau liquide à la même température et à la même pression, 286 kJ de chaleur sont libérés. Si de l’eau gazeuse se forme, seulement 242 kJ de chaleur sont libérés.

H₂ (g) + 1/2 O₂ (g)  →  H₂O (l)     ΔH = – 286 kJ

Une valeur négative d’un changement d’enthalpie, ΔH, indique une réaction exothermique ; une valeur positive de ΔH indique une réaction endothermique (figure 3.4.1). Si le sens d’une équation chimique est inversé, le signe arithmétique de son ΔH est changé (un processus endothermique dans un sens est exothermique dans le sens opposé).

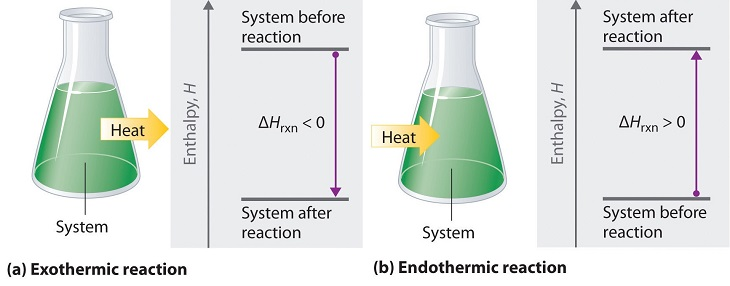
Figure 3.4.1. Les changements d’énergie dans les réactions chimiques sont généralement mesurés comme des changements d’enthalpie. (a) Si la chaleur circule d’un système vers son environnement, l’enthalpie du système diminue, _ΔHrxn est négatif, et la réaction est exothermique ; elle est énergétiquement descendante. (b) Inversement, si la chaleur circule de l’environnement vers un système, l’enthalpie du système augmente, et la réaction est endothermique ; elle est énergétiquement ascendante. (Chem Libre, De :https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_{_}ΔHrxn(Petrucci_et_al.)/07%3A_Thermochemistry/7.6%3A_Heats_of_Reactions_-_%CE%94U_and_%CE%94H , Creative Commons)

Exemple 3.4.1 – Mesure d’un changement d’enthalpie

Lorsque 0,0500 mol de HCl (aq) réagit avec 0,0500 mol de NaOH (aq) pour former 0,0500 mol de NaCl (aq), 2,9 kJ de chaleur sont produits. Qu’est-ce que ΔH, le changement d’enthalpie, par mole d’acide réagissant, pour la réaction acide-base effectuée dans les conditions décrites dans [lien] ?

HCl (aq) + NaOH (aq) → NaCl (aq) + H₂O (l)

Solution

Pour la réaction de 0,0500 mol d’acide (HCl), q = -2,9 kJ. Ce rapport peut être utilisé comme facteur de conversion pour trouver la chaleur produite lorsque 1 mol de HCl réagit :

Le changement d’enthalpie lorsque 1 mol de HCl réagit est de -58 kJ. Comme c’est le nombre de moles dans l’équation chimique, nous écrivons l’équation thermochimique comme suit

HCl (aq) + NaOH (aq)  →  NaCl (aq) + H₂O (l)     ΔH = – 58 kJ

Vérifiez votre apprentissage 3.4.1 – Mesure d’un changement d’enthalpie

Lorsque 1,34 g de Zn (s) réagit avec 60,0 ml de HCl (aq) 0,750 M, 3,14 kJ de chaleur sont produits. Déterminez le changement d’enthalpie par mole de zinc réagissant pour la réaction :

Zn (s) + 2 HCl (aq)  →  ZnCl₂ (aq) + H₂ (g)

Réponse

ΔH = – 153 kJ

Veillez à prendre en compte à la fois la stœchiométrie et les réactifs limitants lorsque vous déterminez le ΔH pour une réaction chimique.

Exemple 3.4.2 – Un autre exemple de mesure d’un changement d’enthalpie

Un ours en gélatine contient 2,67 g de saccharose, C₁₂H₂₂O₁₁. Lorsqu’il réagit avec 7,19 g de chlorate de potassium, KClO₃, 43,7 kJ de chaleur sont produits. Déterminez le changement d’enthalpie pour la réaction :

C₁₂H₂₂O₁₁ (aq) + 8 KClO₃ (aq) → 12 CO_{2 (}g) + 11 H₂O (l) + 8 KCl (aq)

Solution

Nous l’avons fait :

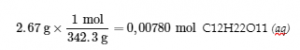
disponible, et

disponible. Depuis

est nécessaire, C12H22O11 est le réactif en excès et KClO3 est le réactif limitant. La réaction utilise 8 mol de KClO3, et le facteur de conversion est

Nous avons donc

Le changement d’enthalpie pour cette réaction est de -5960 kJ, et l’équation thermochimique est :

C₁₂H₂₂O₁₁ (aq) + 8 KClO₃ (aq) → 12 CO_{2 (}g) + 11 H₂O (l) + 8 KCl (aq)

ΔH = – 5960 kJ

Vérifiez votre apprentissage 3.4.2 – Un autre exemple de mesure d’un changement d’enthalpie

Lorsque 1,42 g de fer réagit avec 1,80 g de chlore, 3,22 g de FeCl₂ (s) et 8,60 kJ de chaleur sont produits. Quel est le changement d’enthalpie de la réaction lorsque 1 mol de FeCl₂ (s) est produite ?

Réponse

ΔH = – 338 kJ

Les modifications de l’enthalpie sont généralement présentées sous forme de tableau pour les réactions dans lesquelles les réactifs et les produits sont dans les mêmes conditions. Un état standard est un ensemble de conditions communément acceptées, utilisé comme point de référence pour la détermination des propriétés dans d’autres conditions différentes. Pour les chimistes, l’état standard de l’UICPA fait référence aux matériaux sous une pression de 1 bar et aux solutions à 1 M et ne spécifie pas de température. De nombreux tableaux thermochimiques énumèrent des valeurs avec un état standard de 1 bar. Comme le ΔH d’une réaction change très peu avec de si petites variations de pression (1 bar = 0,987 atm), les valeurs du ΔH (sauf pour les valeurs mesurées avec le plus de précision) sont essentiellement les mêmes dans les deux ensembles de conditions standard. Nous allons inclure un “o” en exposant dans le symbole de changement d’enthalpie pour désigner l’état standard. Comme la température habituelle (mais pas techniquement standard) est de 298,15 K, nous utiliserons un “298” en indice pour désigner cette température (remarque : ceci diffère de la STP pour les gaz, ne les confondez pas !) Ainsi, le symbole (ΔH°₂₉₈) est utilisé pour indiquer un changement d’enthalpie pour un processus se déroulant dans ces conditions. (Le symbole ΔH est utilisé pour indiquer un changement d’enthalpie pour une réaction se produisant dans des conditions non standard).

Les changements d’enthalpie pour de nombreux types de processus chimiques et physiques sont disponibles dans la littérature de référence, y compris ceux pour les réactions de combustion, les transitions de phase et les réactions de formation. Lorsque nous discutons de ces quantités, il est important de prêter attention à la nature étendue de l’enthalpie et des changements d’enthalpie. Comme le changement d’enthalpie pour une réaction donnée est proportionnel aux quantités de substances impliquées, il peut être rapporté sur cette base (c’est-à-dire comme le ΔH pour des quantités spécifiques de réactifs). Cependant, nous trouvons souvent plus utile de diviser une propriété extensive (ΔH) par une autre (quantité de substance), et de déclarer une valeur intensive par quantité de ΔH, souvent “normalisée” sur une base par molécule. (Notez que cela est similaire à la détermination de la chaleur intensive spécifique à une propriété à partir de la capacité thermique d’une propriété extensive, que nous verrons dans le prochain sujet).

Questions

★ Questions

1. Lorsque 100 ml de NaCl 0,200 M (aq) et 100 ml de AgNO₃ 0,200 M (aq), tous deux à 21,9 °C, sont mélangés dans un calorimètre à tasse de café (nous découvrirons à quoi ils servent dans le prochain sujet), la température augmente jusqu’à 23,5 °C au fur et à mesure de la formation d’AgCl solide. Calculer ΔH en kJ/mol de AgNO₃ (aq) pour la réaction :

NaCl (aq) + AgNO₃ (aq) → AgCl (s) + NaNO₃ (aq)

   2. Lorsque le nitrate d’ammonium solide se dissout dans l’eau, la solution devient       froide. C’est la base d’un “ice pack instantanné“. Lorsque 3,21 g de NH₄NO₃ solide     se dissout dans 50,0 g d’eau à 24,9 °C dans un calorimètre, la température                   descend à 20,3 °C. Calculer l’enthalpie de la solution (ΔH pour la dissolution) par       mole de NH₄NO₃.

   3. Comparez qualitativement ΔH et ΔU pour chacune des réactions suivantes :

         a. AgNO₃ (aq) + NaCl (aq)  →  AgCl (s) + NaNO₃ (aq)

         b. H₂ (g) + F₂ (g)  →  2 HF (g)

         c. C₃H₈ (g) + 5 O₂ (g)  →  3 CO₂ (g) + 4 H₂O (g)

   4. Calculer ΔH pour la réaction décrite par l’équation. (Conseil : utilisez la valeur           pour la quantité approximative de chaleur absorbée par la réaction que vous avez     calculée dans un exercice précédent).

Ba(OH)₂ ∙ 8H₂O (s) + 2 NH₄SCN (aq)  →  Ba(SCN)₂ (aq) + 2 NH₃ (aq) + 10 H₂O (l)

   5. Quelle est la quantité de chaleur produite par la combustion de 125 g de                   méthanol dans des conditions normales ?

   6. Combien de moles d’isooctane doivent être brûlées pour produire 100 kJ de             chaleur dans des conditions d’état standard ?

   7. Quelle masse de monoxyde de carbone doit être brûlée pour produire 175 kJ de       chaleur dans des conditions d’état standard ?

   8. Lorsque 2,50 g de méthane brûlent dans l’oxygène, 125 kJ de chaleur sont               produits. Quelle est l’enthalpie de combustion par mole de méthane dans ces             conditions ?

Réponses

1. 1,34 x 10³ kJ/mol

Nous supposons que le calorimètre empêche le transfert de chaleur entre la solution et son environnement externe (y compris le calorimètre lui-même), auquel cas :

q_rxn = – q_soln

avec “rxn” et “soln” utilisés comme abréviations pour “réaction” et “solution”, respectivement.

En supposant également que la chaleur spécifique de la solution est la même que celle de l’eau, nous avons :

q_rxn = – q_soln = – (c × m × ΔT)_soln

= [(4,184 J/g^∘C) × (53,2 g) × (20.3^∘C – 24.9^∘C)]

= [(4,184 J/g^∘C) × (53,2 g) × (- 4.6^∘C)]

+ 1,0 × 10³ J = + 1,0 kJ

Le signe positif pour q indique que la dissolution est un processus endothermique.

   3. (a) ΔU ≈ ΔH : comme il n’y a pas de gaz, la variation de volume est négligeable       (fondamentalement égale à 0), ce qui signifie que ΔU ≈ qP et comme ΔH = qP           alors ΔU ≈ ΔH ; (b) ΔU = ΔH : Δn = 0 mol ce qui signifie qu’il n’y a pas de travail           effectué, donc ΔU = ΔH ; (c) ΔU > ΔH : Δn = 1 mol ce qui donne w = – RT. – La RT         sera toujours négative donc, sous une pression constante, ΔU = ΔH – RT                     démontrant ΔU > ΔH.

   4. 95,72 kJ/mol

   5. 2836,3 kJ

   6. 1,83 × 10^-2 mol

   7. 17,3 g

   8. 802 kJ mol^-1