3.3 – Première loi de la thermodynamique

La relation entre l’énergie interne, la chaleur et le travail peut être représentée par l’équation :

ΔU = q + w

Il s’agit d’une version de la première loi de la thermodynamique qui stipule que “l’énergie n’est ni créée ni détruite, mais seulement transférée”, et elle montre que l’énergie interne d’un système change par le flux de chaleur entrant ou sortant du système (q positif est le flux de chaleur entrant ; q négatif est le flux de chaleur sortant) ou que des travaux sont effectués sur ou par le système. Le travail, w, est positif s’il est effectué sur le système et négatif s’il est effectué par le système. Dans le cas du travail PV, nous pouvons considérer le travail effectué sur le système comme une contraction, tandis que le travail effectué par le système est une expansion.

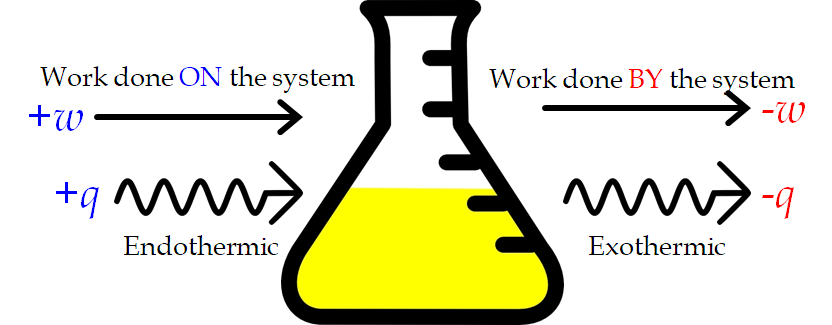
Figure 3.3.1. Signes des conventions pour la chaleur et le travail. Les travaux effectués sur le système ou la chaleur absorbée par le système sont positifs. Le travail effectué par le système ou la chaleur produite par le système sont négatifs. Cela peut se produire dans n’importe quelle combinaison.

Comme nous l’avons vu au point 3.1, l’énergie dans l’univers est constante/fixe. Nous pouvons établir un lien avec l’énergie interne en disant que, si l’énergie peut être transférée entre le système et l’environnement, la variation de l’énergie interne de l’univers est égale à zéro.

ΔU_univers = ΔU_système + ΔU_environs = 0

Il existe de nombreuses formes de travail comme le travail électrique et mécanique, mais dans ce cours, le type de travail concerné est appelé travail d'expansion (ou travail pression-volume). Le travail d’expansion se produit lorsqu’un système repousse l’environnement contre une pression de retenue, ou lorsque l’environnement comprime le système. Un exemple de ce type de travail se produit lors du fonctionnement d’un moteur à combustion interne. La réaction de l’essence et de l’oxygène est exothermique. Une partie de cette énergie est dégagée sous forme de chaleur, et une autre partie agit en poussant le piston dans le cylindre. Les substances impliquées dans la réaction sont le système, et le moteur et le reste de l’univers sont l’environnement. Le système perd de l’énergie en chauffant et en travaillant sur l’environnement, et son énergie interne diminue. Nous verrons comment déterminer la quantité de travail impliquée dans un changement chimique ou physique dans le chapitre sur la thermodynamique.

Cette vue d’un moteur à combustion interne illustre la conversion de l’énergie produite par la réaction de combustion exothermique d’un carburant tel que l’essence en énergie de mouvement. Pour en savoir plus sur la première loi de la thermodynamique, regardez cette vidéo.

Fonctions d’États

Comme nous l’avons vu, la relation entre l’énergie interne, la chaleur et le travail peut être représentée comme suit : ΔU = q + w. L‘énergie interne est un type de quantité connu sous le nom de fonction d'état, alors que la chaleur et le travail ne sont pas des fonctions d’état (généralement appelées fonctions de chemin). La valeur d’une fonction d’état dépend uniquement de l’état dans lequel se trouve un système, et non de la manière dont cet état est atteint. Si une quantité n’est pas une fonction d’état, alors sa valeur dépend de la manière dont l’état est atteint. Un exemple de fonction d’état est l’altitude ou l’élévation. Si vous vous trouvez au sommet du Kilimandjaro, vous êtes à une altitude de 5895 m, peu importe que vous y ayez fait de la randonnée ou du parachutisme. La distance que vous avez parcourue pour atteindre le sommet du Kilimandjaro n’est cependant pas une fonction d’état. Vous pouvez monter au sommet par une route directe ou par un chemin plus détourné et plus sinueux (figure 3.3.2.). Les distances parcourues seraient différentes (la distance n’est pas une fonction d’état) mais l’altitude atteinte serait la même (l’altitude est une fonction d’état).

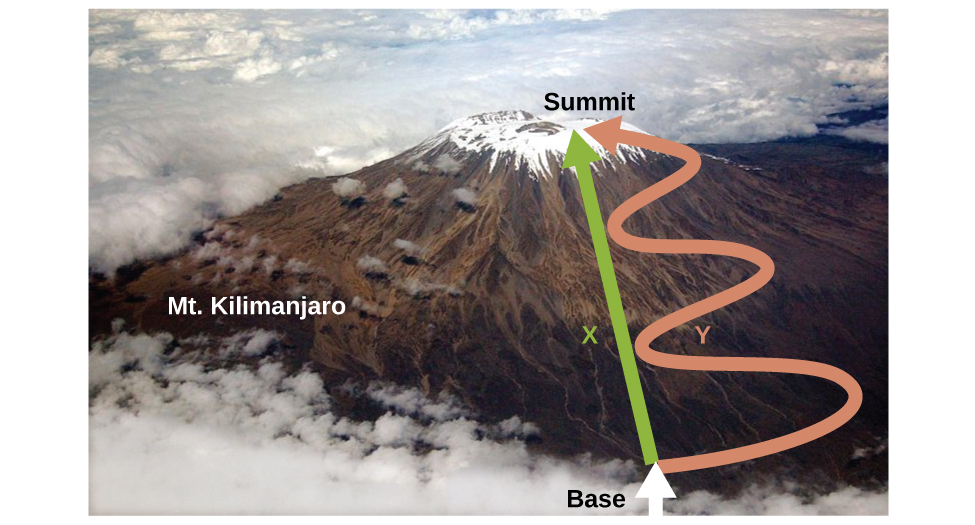
Figure 3.3.2. Les chemins X et Y représentent deux itinéraires différents vers le sommet du Mt Kilimandjaro. Tous deux ont le même changement d’altitude (l’altitude ou l’élévation sur une montagne est une fonction d’état ; elle ne dépend pas du chemin), mais ils ont des distances parcourues très différentes (la distance parcourue n’est pas une fonction d’état ; elle dépend du chemin). (crédit : modification de l’ouvrage de Paul Shaffner)

En ce qui concerne l’énergie, le travail et la chaleur sont tous deux des fonctions de chemin, mais l’énergie interne ne l’est pas. Cela signifie que le chemin emprunté pour atteindre les résultats est important lors du calcul de w ou q, mais ne doit pas être pris en compte lors de la résolution pour ΔU.

Diagrammes énergétiques

Lorsque l’on travaille avec des systèmes impliquant à la fois chaleur et travail, il est souvent utile de visualiser la transition entre l’état énergétique initial et l’état énergétique final à l’aide d’un diagramme (figure 3.3.3.).

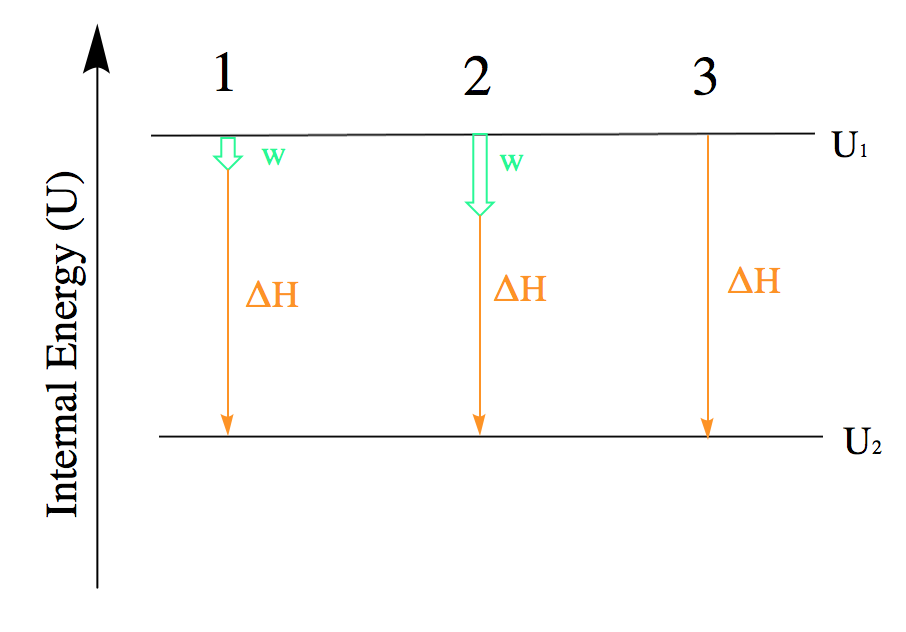
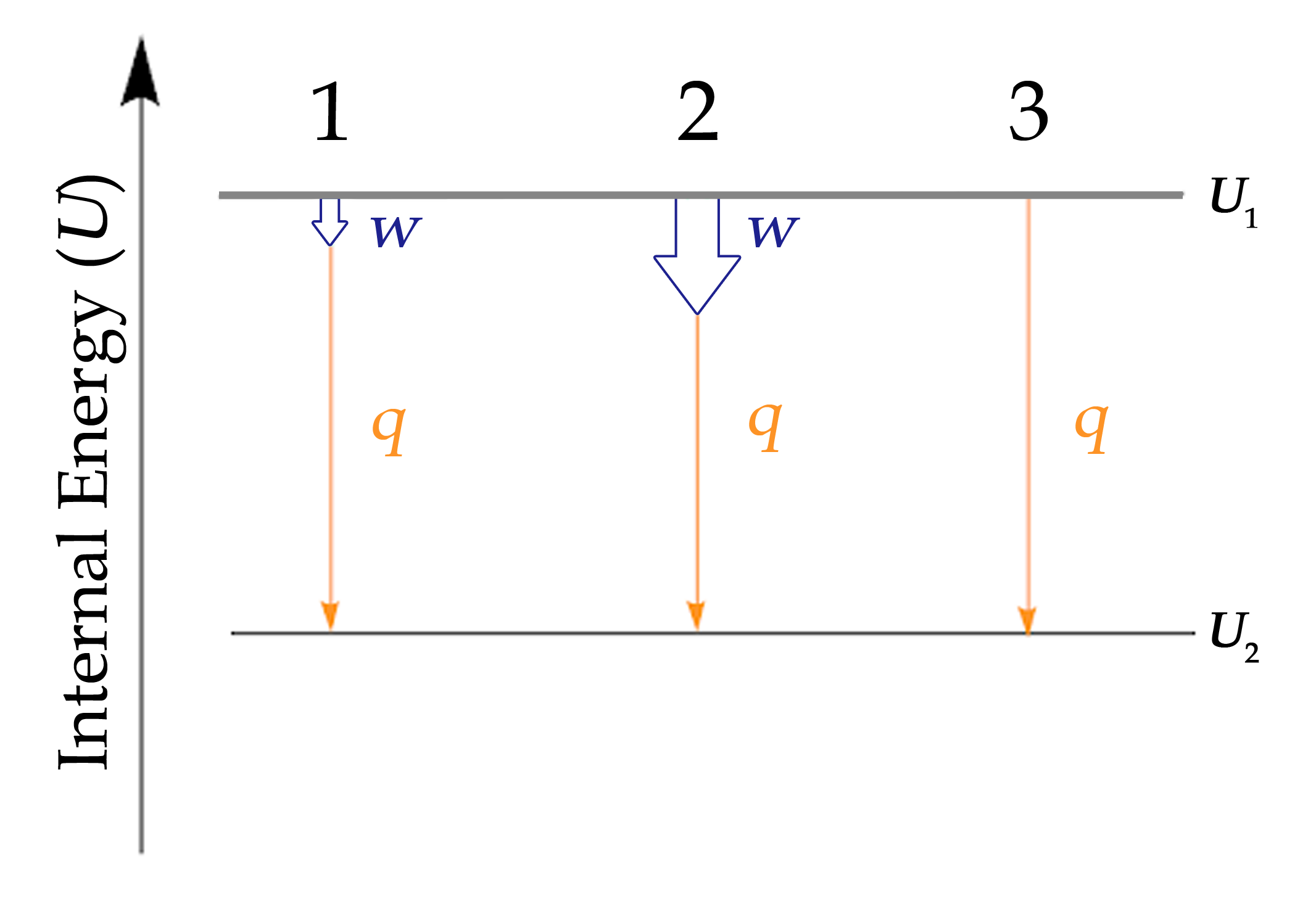
Figure 3.3.3. L’énergie interne de trois processus dont le système perd de l’énergie. 1 : Représentation de la variation de l’énergie interne essentiellement égale au transfert de chaleur. Mathématiquement : ΔU ≈ q. 2 : Représentation de la variation de l’énergie interne lorsque le travail est effectué et que la chaleur est perdue. Mathématiquement : ΔU = q + w. 3 : Représentation de la variation de l’énergie interne lorsqu’aucun travail n’est effectué mais que de la chaleur est perdue. Mathématiquement : ΔU = q

Bien que la figure 3.3.3. ne montre que les processus pour lesquels un système perd de l’énergie, cette tactique doit être utilisée chaque fois que possible et peut être modifiée pour les cas où le travail et la chaleur présentent des signes différents. La loi de Hess traitera davantage de ce point.

Questions

★ Questions

1. On laisse un échantillon d’un gaz idéal se dilater d’un volume initial de 0,200 L à un volume final de 3,50 L contre une pression extérieure constante de 0,995 atm. Dans le même temps, 117 J de chaleur sont transférés de l’environnement au gaz. Quelle est la variation totale de l’énergie interne (ΔU) du gaz en joules ?

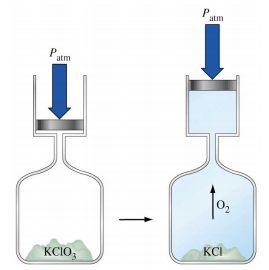
2. Lorsque le chlorate de potassium se décompose, il produit de l’oxygène gazeux.     Du point de vue du système (ce qui est la convention), w est : 

            A. Positif

B. Négatif

C. Zéro

   3. Quel est le travail lorsqu’un gaz se contracte de 3,45 L à 0,97 L sous une                   pression extérieure de 0,985 atm ?

★★ Questions

   4. Le volume d’un gaz passe de 264 ml à 971 ml à température constante. Calculer     la quantité de travail effectuée par le gaz (en joules) s’il se dilate (a) contre un vide     et (b) contre une pression constante de 4,00 atm.

   5. Pour les réactions suivantes, indiquez si le travail va augmenter, diminuer ou           rester constant. Conseil : n’oubliez pas que le travail est basé sur la PV – comment     le volume change-t-il dans chaque réaction ?

         a. 2 H₂O (l)  →  2 H₂ (g) + O₂ (g)

         b. NO₂ (g) + O₃ (g)  →  NO₃ (g) + O₂ (g)

         c. CH₄ (g) + 2 O₂ (g)  →CO_{2 (}g) + 2 H₂O (l)

Réponses

1. -216 J
2. B
3. 248 J
4. (a) 0 J, aucun travail n’est effectué ; (b) -287 J
5. (a) w augmente parce que les moles de gaz augmentent, ce qui augmenterait le volume de gaz. (b) il n’y a pas de changement parce que les deux côtés de la réaction ont le même nombre de moles de gaz. (c) diminue en raison des quantités différentes de gaz des deux côtés de la réaction, le côté réactif ayant un plus grand nombre de moles de gaz.