2.8 – Comportements des gaz réels/non-idéaux

Jusqu’à présent, la loi du gaz idéal, PV = nRT, a été appliquée à différents types de problèmes, allant de la stœchiométrie des réactions et des problèmes de formules empiriques et moléculaires à la détermination de la densité et de la masse molaire d’un gaz. Cependant, comme mentionné dans les modules précédents de ce chapitre, le comportement d’un gaz est souvent non idéal, ce qui signifie que les relations observées entre sa pression, son volume et sa température ne sont pas décrites avec précision par les lois des gaz. Dans cette section, les raisons de ces écarts par rapport au comportement idéal du gaz sont examinées.

Une façon de juger de la précision de PV = nRT consiste à comparer le volume réel d’une mole de gaz (son volume molaire, V_m) au volume molaire d’un gaz idéal à la même température et à la même pression. Ce rapport est appelé le facteur de compressibilité (Z) avec :

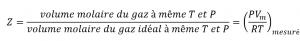
Équation 2.8.1 Facteur de compressibilité

Le comportement idéal du gaz est donc indiqué lorsque ce rapport est égal à 1, et tout écart par rapport à 1 est une indication de comportement non idéal. La figure 2.8.1. montre des graphiques de Z sur une large gamme de pression pour plusieurs gaz courants.

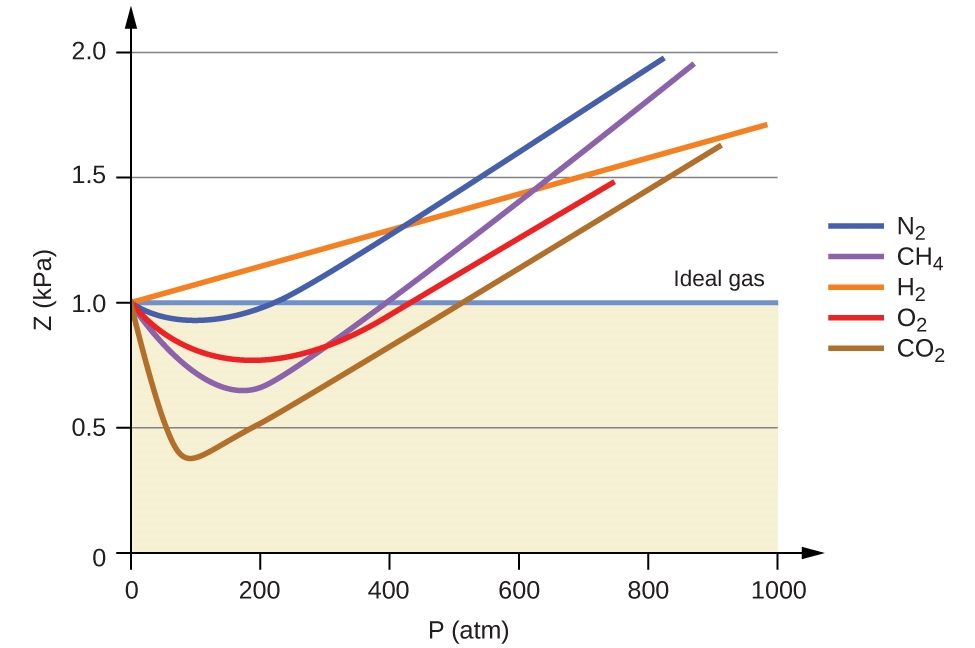
Figure 2.8.1. Un graphique du facteur de compressibilité (Z) en fonction de la pression montre que les gaz peuvent présenter des écarts importants par rapport au comportement prévu par la loi des gaz idéaux. Pour examiner ce comportement plus près de l’origine, consultez la page 3 des notes de cours suivantes.

Comme le montre la figure 2.8.1., la loi du gaz idéal ne décrit pas bien le comportement du gaz à des pressions relativement élevées. Pour en déterminer la raison, il faut considérer les différences entre les propriétés réelles du gaz et ce que l’on attend d’un gaz idéal hypothétique.

Les particules d’un gaz idéal hypothétique n’ont pas de volume significatif et ne s’attirent ni ne se repoussent. En général, les gaz réels se rapprochent de ce comportement à des pressions relativement basses et à des températures élevées. Cependant, à des pressions élevées, les particules d’un gaz sont plus proches les unes des autres et l’espace vide entre les particules est réduit. À ces pressions plus élevées, le volume des particules de gaz elles-mêmes devient appréciable par rapport au volume total occupé par le gaz (figure 2.8.2.). Le gaz devient donc moins compressible à ces hautes pressions, et bien que son volume continue à diminuer avec l’augmentation de la pression, cette diminution n’est pas proportionnelle comme le prédit la loi de Boyle.

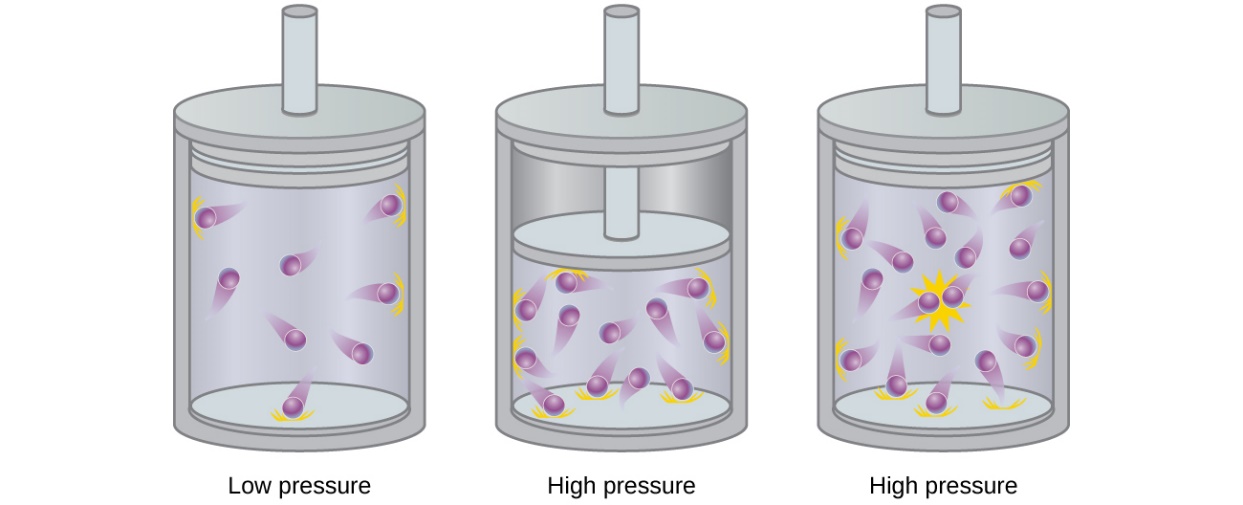
Figure 2.8.2. L’augmentation de la pression d’un gaz augmente la fraction de son volume qui est occupée par les particules de gaz et rend le gaz moins compressible. Ici, l’augmentation de la pression est obtenue soit (b) en diminuant le volume du récipient, soit (c) en augmentant la quantité de gaz dans le récipient. Dans les deux cas, des écarts par rapport au comportement idéal peuvent apparaître.

À des pressions relativement basses, les particules de gaz n’ont pratiquement aucune attraction les unes pour les autres car elles sont (en moyenne) très éloignées les unes des autres et elles ont tendance à se comporter comme les particules d’un gaz idéal. À des pressions plus élevées, cependant, la force d’attraction n’est plus insignifiante non plus. Cette force rapproche un peu plus les particules les unes des autres, en diminuant légèrement la pression (si le volume est constant) ou en diminuant le volume (si la pression est constante) (figure 2.8.3.). Ce changement est plus prononcé à basse température, car les particules ont un E_k plus faible par rapport aux forces d’attraction, et elles sont donc moins efficaces pour surmonter ces attractions après être entrées en collision les unes avec les autres.

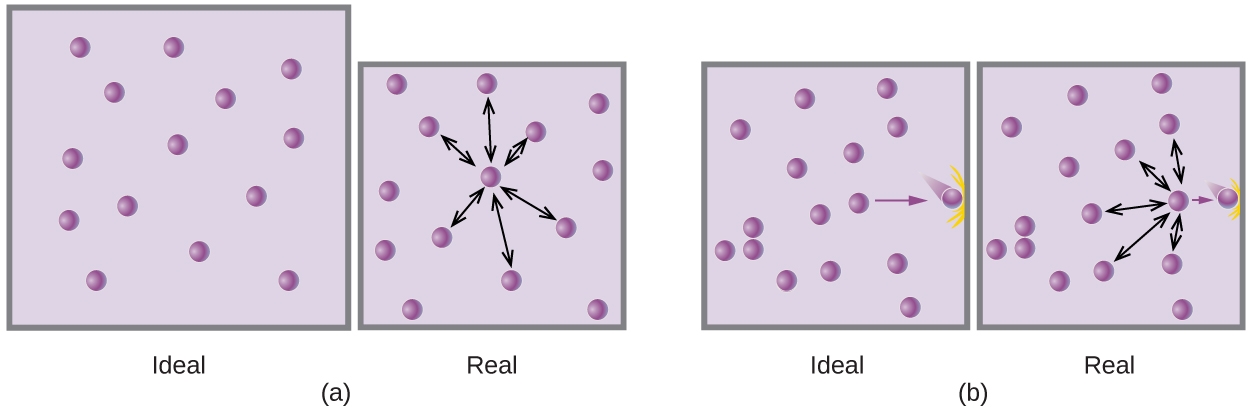
Figure 2.8.3. (a) Les attractions entre les particules de gaz servent à diminuer le volume de gaz à pression constante par rapport à un gaz idéal dont les particules ne subissent aucune force d’attraction. (b) Ces forces d’attraction diminuent la force des collisions entre les particules et les parois du récipient, réduisant ainsi la pression exercée par rapport à un gaz idéal.

Il existe plusieurs équations différentes qui se rapprochent davantage du comportement du gaz que ne le fait la loi idéale du gaz. La première, et la plus simple, a été développée par le scientifique néerlandais Johannes van der Waals en 1879. L’équation de van der Waals améliore la loi idéale du gaz en ajoutant deux termes : un facteur de correction pour tenir compte du volume des particules de gaz et un autre pour les forces d’attraction entre elles.

Équation 2.8.2 Van der Waals

La constante a correspond à la force de l’attraction entre les particules d’un gaz particulier, et la constante b correspond à la taille des particules d’un gaz particulier. La correction du terme de pression dans la loi du gaz idéal est et la correction du volume est nb. Notez que lorsque V est relativement grand et n est relativement petit, ces deux termes de correction deviennent négligeables, et l’équation de van der Waals se réduit à la loi idéale du gaz, PV = nRT. Une telle condition correspond à un gaz dans lequel un nombre relativement faible de particules occupe un volume relativement important, c’est-à-dire un gaz à une pression relativement basse. Les valeurs expérimentales des constantes de van der Waals de certains gaz courants sont données dans le tableau 2.8.1.

Tableau 2.8.1 Constantes de Van der Waals. Pour plus de constantes de van der Waals, suivez le lien suivant.

À basse pression, la correction pour l’attraction intermoléculaire, a, est plus importante que celle pour le volume moléculaire, b. À haute pression et petits volumes, la correction pour le volume des particules devient importante parce que les particules elles-mêmes sont incompressibles et constituent une fraction appréciable du volume total. À une certaine pression intermédiaire, les deux corrections ont des influences opposées et le gaz semble suivre la relation donnée par PV = nRT sur une petite plage de pressions. Ce comportement se reflète dans les “creux” de plusieurs des courbes de compressibilité présentées à la figure 2.8.4. La force d’attraction entre les particules rend initialement le gaz plus compressible qu’un gaz idéal, à mesure que la pression augmente (Z diminue avec l’augmentation de P). À des pressions très élevées, le gaz devient moins compressible (Z augmente avec P), car les particules de gaz commencent à occuper une fraction de plus en plus importante du volume total du gaz.

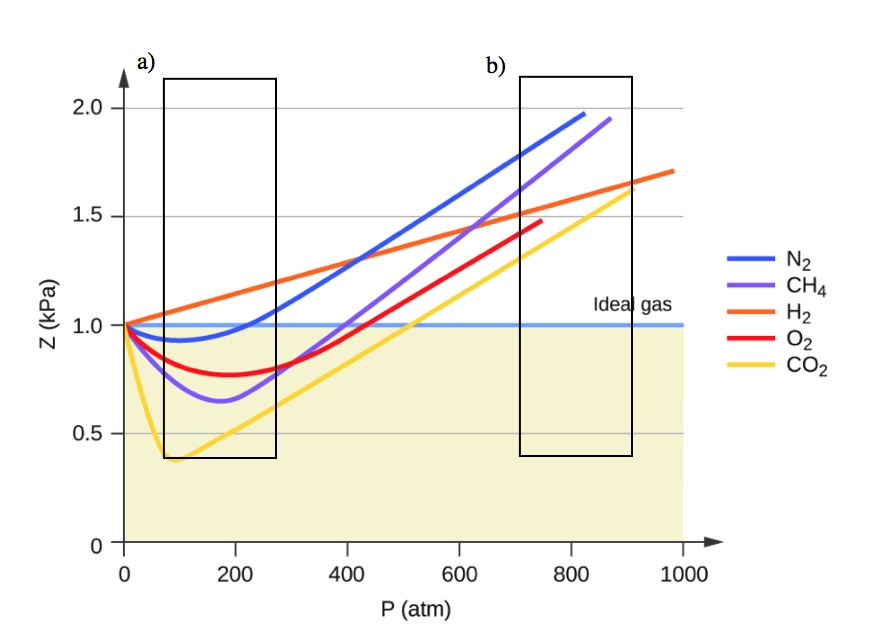
Figure 2.8.4. Un graphique du facteur de compressibilité (Z) en fonction de la pression montre que les gaz peuvent présenter des écarts importants par rapport au comportement prévu par la loi du gaz idéal. a) montre où l’attraction intermoléculaire (a) a le plus d’impact sur l’équation du gaz idéal, et b) montre où le volume des particules (b) a le plus d’impact sur l’équation du gaz idéal

À proprement parler, l’équation du gaz idéal fonctionne bien lorsque les attractions intermoléculaires entre les particules de gaz sont négligeables et que les particules de gaz elles-mêmes n’occupent pas une partie appréciable du volume total. Ces critères sont satisfaits dans des conditions de basse pression et de haute température. Dans ces conditions, on dit que le gaz se comporte idéalement et que les écarts par rapport aux lois du gaz sont suffisamment faibles pour qu’ils puissent être ignorés – ce qui n’est cependant pas souvent le cas.

Exemple 2.8.1 – Comparaison de la loi du gaz idéal et de l’équation de van der Waals

Un ballon de 4,25 litres contient 3,46 moles de CO₂ à 229 °C. Calculez la pression de cet échantillon de CO₂ :

a) de la loi idéale sur le gaz

b) de l’équation de van der Waals

(c) Expliquez la ou les raisons de la différence.

Solution

(a) De la loi idéale sur le gaz :

(b) De l’équation de van der Waals :

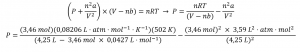
Cela donne finalement P = 32,4 atm.

(c) Cette valeur n’est pas très différente de celle de la loi idéale des gaz car la pression n’est pas très élevée et la température n’est pas très basse. La valeur est quelque peu différente parce que les particules de CO₂ ont un certain volume et des attractions entre les particules, et la loi du gaz idéal suppose qu’elles n’ont pas de volume ou d’attractions.

Vérifiez votre apprentissage 2.8.1 – Comparaison de la loi du gaz idéal et de l’équation de van der Waals

Un ballon de 560 ml contient 21,3 g de N₂ à 145 °C. Calculer la pression de N₂ :

a) de la loi idéale sur le gaz

b) de l’équation de van der Waals

(c) Expliquez la ou les raisons de la différence.

Réponse

(a) 46,562 atm ; (b) 46,594 atm ; (c) L’équation de van der Waals prend en compte le volume des particules de gaz elles-mêmes ainsi que les attractions intermoléculaires.

Questions

★ Questions

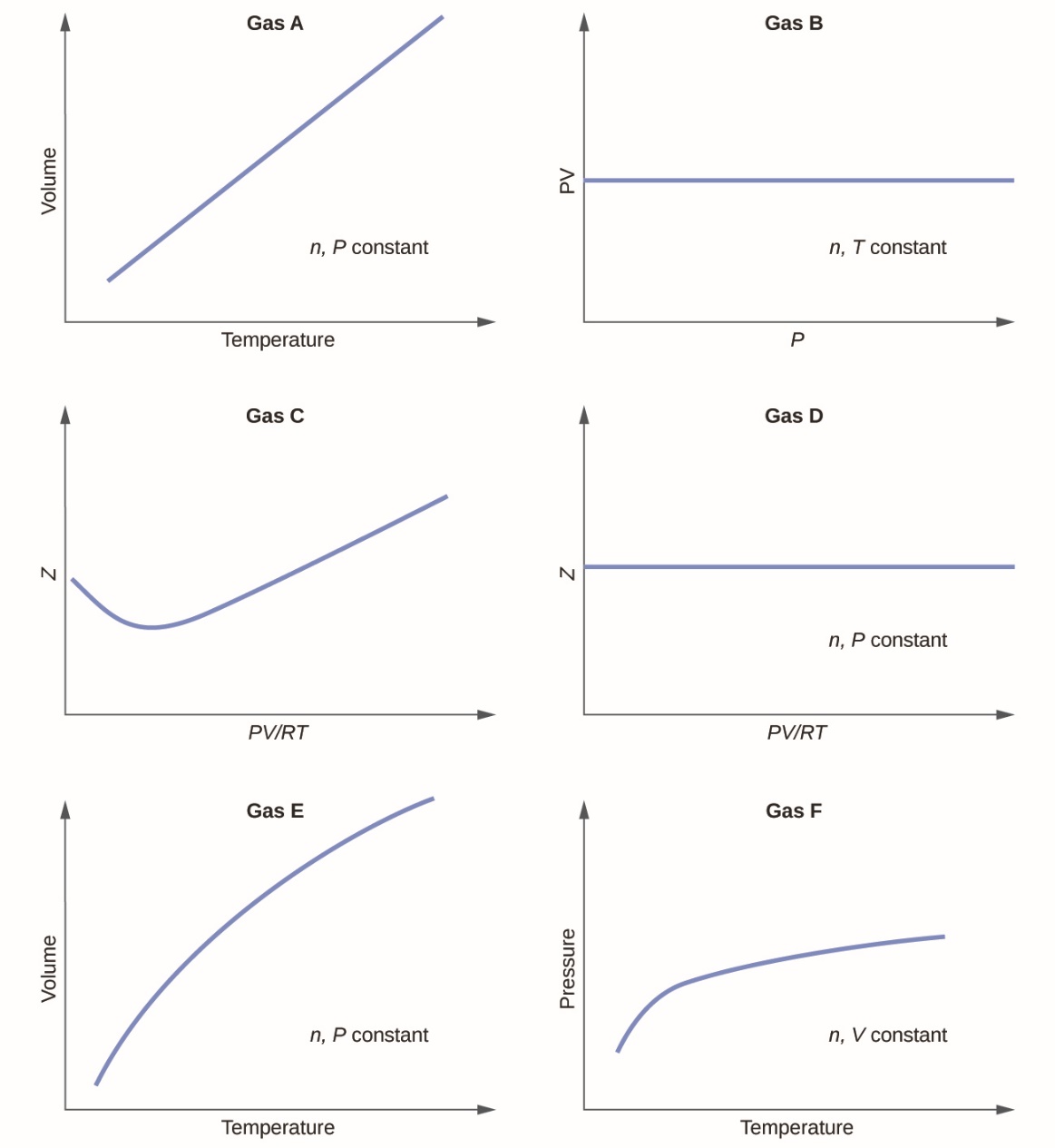
1. Les graphiques suivants montrent le comportement de plusieurs gaz différents. Lesquels de ces gaz ont un comportement significativement différent de celui attendu pour les gaz idéaux ?

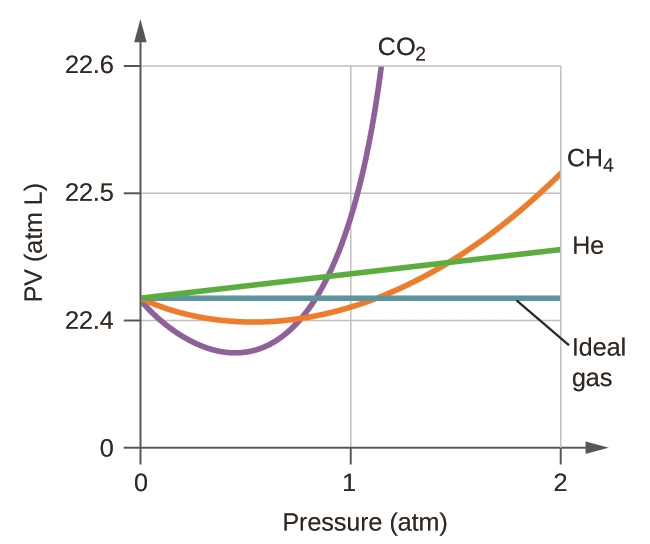
2. Expliquez pourquoi le tracé de la PV pour le CO₂ diffère de celui d’un gaz idéal.

3. Dans quelles conditions un gaz réel se comporte-t-il le plus comme un gaz idéal, et dans quelles conditions un gaz réel devrait-il s’écarter de son comportement idéal? Expliquez.

a. haute pression, petit volume

b. haute température, basse pression

c. basse température, haute pression

4. Décrire les facteurs responsables de la déviation du comportement des gaz réels par rapport à celui d’un gaz idéal.

5. Pour lequel des gaz suivants la correction pour le volume moléculaire devrait être la plus importante : CO, CO_2, H_2, He, NH₃, SF₆?

6. Un ballon de 0,245 L contient 0,467 mol de CO₂ à 159 °C. Calculer la pression :

a. utiliser la loi idéale sur le gaz

b. en utilisant l’équation de van der Waals

c. Expliquez la raison de cette différence.

d. Identifiez quelle correction (celle pour P ou V) est dominante et pourquoi.

★★ Questions

7. Répondez aux questions suivantes :

a. Si XX se comportait comme un gaz idéal, à quoi ressemblerait son graphique de Z contre P ?

b. Pour la plus grande partie de ce chapitre, nous avons effectué des calculs en considérant les gaz comme idéaux. Cela était-il justifié ?

c. Quel est l’effet du volume des molécules de gaz sur Z? Dans quelles conditions cet effet est-il faible ? Quand est-il important ? Expliquez à l’aide d’un diagramme approprié.

d. Quel est l’effet des attractions intermoléculaires sur la valeur de Z? Dans quelles conditions cet effet est-il faible ? Quand est-il important ? Expliquez à l’aide d’un diagramme approprié.

e. En général, dans quelles conditions de température s’attendriez-vous à ce que Z présente les plus grands écarts par rapport à Z pour un gaz idéal ?

Réponses

1. Gaz C, E et F

2. Le CO₂ interagit de manière intermoléculaire avec d’autres molécules et occupe un volume dans l’espace. Les molécules de CO₂ repoussent donc d’autres molécules et créent une pression par le biais de collisions, ce qui entraîne une relation non linéaire entre PV et P.

3. Le comportement du gaz le plus proche d’un gaz idéal se produira dans les conditions décrites au point (b). Les molécules ont des vitesses élevées et se déplacent sur de plus grandes distances entre les collisions ; elles ont également des temps de contact plus courts et les interactions sont moins probables. Des écarts se produisent dans les conditions décrites aux points (a) et (c). Dans les conditions de (a), certains gaz peuvent se liquéfier. Dans les conditions de (c), la plupart des gaz se liquéfieront.

4. On suppose qu’un gaz idéal n’a pas de volume ou d’interaction intermoléculaire. Les molécules qui décrivent le comportement réel du gaz montrent une attraction entre d’autres molécules, ce qui entraîne une déviation du comportement idéal du gaz. Les gaz réels ne présentent un comportement idéal qu’à des températures élevées et des pressions basses.

5. SF₆

6. (a) 66,2 atm, (b) 60,5 atm, (c) van der Waals tient compte des facteurs de gaz non idéaux (forces répulsives et occupation du volume) que la loi du gaz idéal ne prend pas en compte, (d) Le facteur de correction de pression utilisé dans le van der Waals est dominant dans les cas de basse pression. Pour les volumes plus importants, la pression est également plus élevée.

7. (a) Une ligne droite horizontale à 1,0 ; (b) Lorsque les gaz réels sont à basse pression et à haute température, ils se comportent suffisamment près des gaz idéaux pour être approximés comme tels, cependant, dans certains cas, on constate qu’à une pression et une température élevée, l’approximation du gaz idéal se décompose et est sensiblement différente de la pression calculée par l’équation du gaz idéal (c) Plus la compressibilité est grande, plus le volume importe. À basse pression, le facteur de correction des attractions intermoléculaires est plus important, et l’effet du volume des molécules de gaz sur Z serait une légère baisse de la compressibilité. À des pressions plus élevées, l’effet du volume des molécules de gaz elles-mêmes sur Z augmenterait la compressibilité (d) Une fois de plus, à basse pression, l’effet des attractions intermoléculaires sur Z serait plus important que le facteur de correction du volume des molécules de gaz elles-mêmes, bien qu’il soit peut-être encore faible. À des pressions plus élevées et à des températures plus basses, l’effet des attractions intermoléculaires serait plus important. e) basses températures