2.7 – Diffusion et effusion
Tu es avec tes amis en attendant qu’une pizza arrive. On sonne à la porte, et l’un de tes amis se lève pour ouvrir la porte et recevoir la bonne humeur. Quelques secondes après et peut-être même avant que la porte ne s’ouvre, vous pouvez déjà sentir son incroyable arôme. La vitesse rapide à laquelle l’arôme se propage de la porte à votre nez est due à la nature des gaz – les molécules gazeuses peuvent se répandre rapidement dans une pièce. Dans cette section, nous abordons le processus de diffusion et d’effusion des gaz comme une application du TCM.
Diffusion
Bien que les molécules gazeuses se déplacent à des vitesses énormes (des centaines de mètres par seconde), elles entrent en collision avec d’autres molécules gazeuses et se déplacent dans de nombreuses directions différentes avant d’atteindre la cible souhaitée. À température ambiante, une molécule gazeuse subira des milliards de collisions par seconde. Le trajet libre moyen est la distance moyenne parcourue par une molécule entre deux collisions. Le libre parcours moyen augmente avec la diminution de la pression ; en général, le libre parcours moyen d’une molécule gazeuse sera des centaines de fois plus grand que le diamètre de la molécule.
En général, nous savons que lorsqu’un échantillon de gaz est introduit dans une partie d’un récipient fermé, ses molécules se dispersent très rapidement dans le récipient ; ce processus par lequel les molécules se dispersent dans l’espace en réponse à des différences de concentration est appelé diffusion (voir figure 2.7.1). Les atomes ou molécules gazeux ne connaissent bien sûr aucun gradient de concentration, ils se déplacent simplement au hasard – les régions de plus forte concentration contiennent plus de particules que les régions de plus faible concentration, et il se produit donc un mouvement net des zones de forte concentration vers les zones de faible concentration. Dans un environnement fermé, la diffusion se traduira en fin de compte par des concentrations égales de gaz partout, comme le montre la figure 2.7.1. Les atomes et les molécules gazeuses continuent à se déplacer, mais comme leurs concentrations sont les mêmes dans les deux ampoules, les taux de transfert entre les ampoules sont égaux (il n’y a pas de transfert net de molécules).
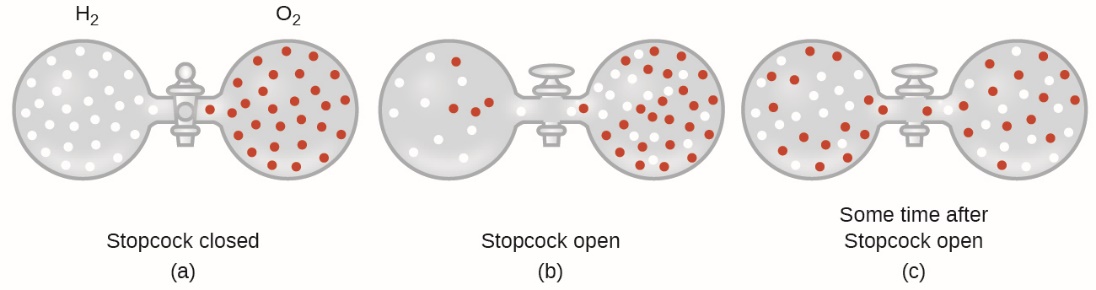
Figure 2.7.1. (a) Deux gaz, H2 et O2, sont initialement séparés. (b) Lorsque le robinet est ouvert, ils se mélangent. Le gaz le plus léger, H2, traverse l’ouverture plus rapidement que O2, de sorte que juste après l’ouverture du robinet, plus de molécules de H2 se déplacent vers le côté O2 que de molécules de O2 se déplacent vers le côté H2. (c) Après un court laps de temps, les molécules d’O2 se déplaçant plus lentement et les molécules d’H2 se déplaçant plus rapidement se sont réparties de manière égale des deux côtés du récipient.
Nous nous intéressons souvent au taux de diffusion, à la quantité de gaz passant dans une zone donnée par unité de temps :
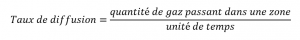
Équation 2.7.1 Taux de diffusion
La vitesse de diffusion dépend de plusieurs facteurs : le gradient de concentration (l’augmentation ou la diminution de la concentration d’un point à un autre), la surface disponible pour la diffusion et la distance que les particules de gaz doivent parcourir. Notez également que le temps nécessaire pour que la diffusion se produise est inversement proportionnel à la vitesse de diffusion, comme le montre l’équation de la vitesse de diffusion.
Effusion
Un processus impliquant le déplacement d’espèces gazeuses similaire à la diffusion est l’effusion, l’échappement de molécules de gaz par un minuscule trou tel qu’un trou d’épingle dans un ballon dans un vide (figure 2.7.2). Bien que les taux de diffusion et d’effusion dépendent tous deux de la masse molaire du gaz concerné, leurs taux ne sont pas égaux ; cependant, les rapports de leurs taux sont les mêmes.
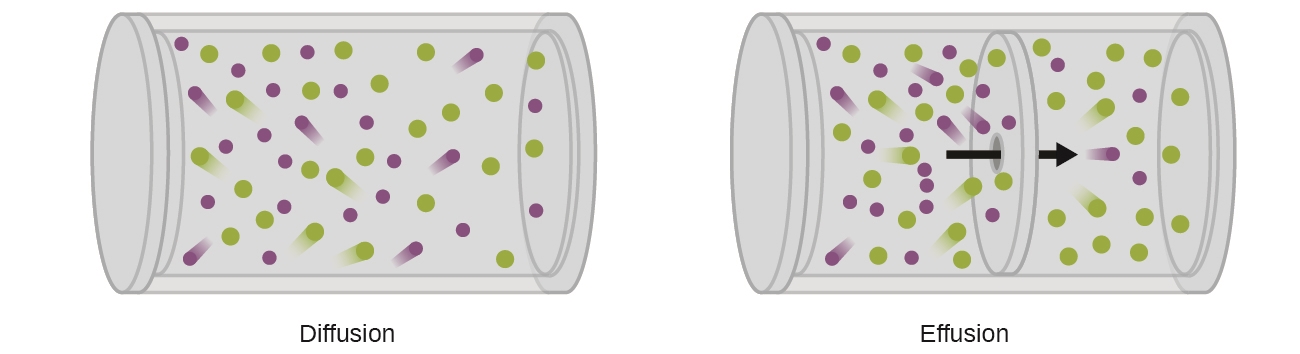
Figure 2.7.2. La diffusion se produit lorsque les molécules de gaz se dispersent dans un récipient. L’effusion se produit lorsqu’un gaz passe par une ouverture plus petite que le trajet libre moyen des particules, c’est-à-dire la distance moyenne parcourue entre les collisions. En fait, cela signifie qu’une seule particule passe à travers à la fois.
Si deux gaz de masses de particules différentes sont placés dans des chambres fermées séparées, chacune avec une paroi contenant un seul trou d’épingle, les deux gaz s’écouleront progressivement par la petite ouverture dans la paroi. Toutefois, le gaz le plus léger passe plus rapidement (à un rythme plus élevé) par la petite ouverture que le plus lourd (figure 2.7.3). En 1832, Thomas Graham a étudié les taux d’effusion de différents gaz et a formulé la loi d'effusion de Graham : Le taux d’effusion d’un gaz est inversement proportionnel à la racine carrée de la masse de ses particules :
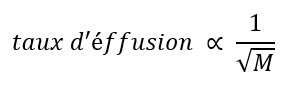
Équation 2.7.2 Taux d’éffusion
Cela signifie que si deux gaz A et B sont à la même température et à la même pression, le rapport de leurs taux d’effusion est inversement proportionnel au rapport des racines carrées des masses de leurs particules :
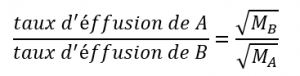
Notez que, lorsque la loi de Graham est utilisée sous cette forme, vous pouvez utiliser des masses molaires exprimées soit en kg/mol, soit en g/mol, car les unités s’annulent. De même, d’autres unités qui sont directement proportionnelles à la masse du gaz, comme la densité, peuvent également être utilisées.
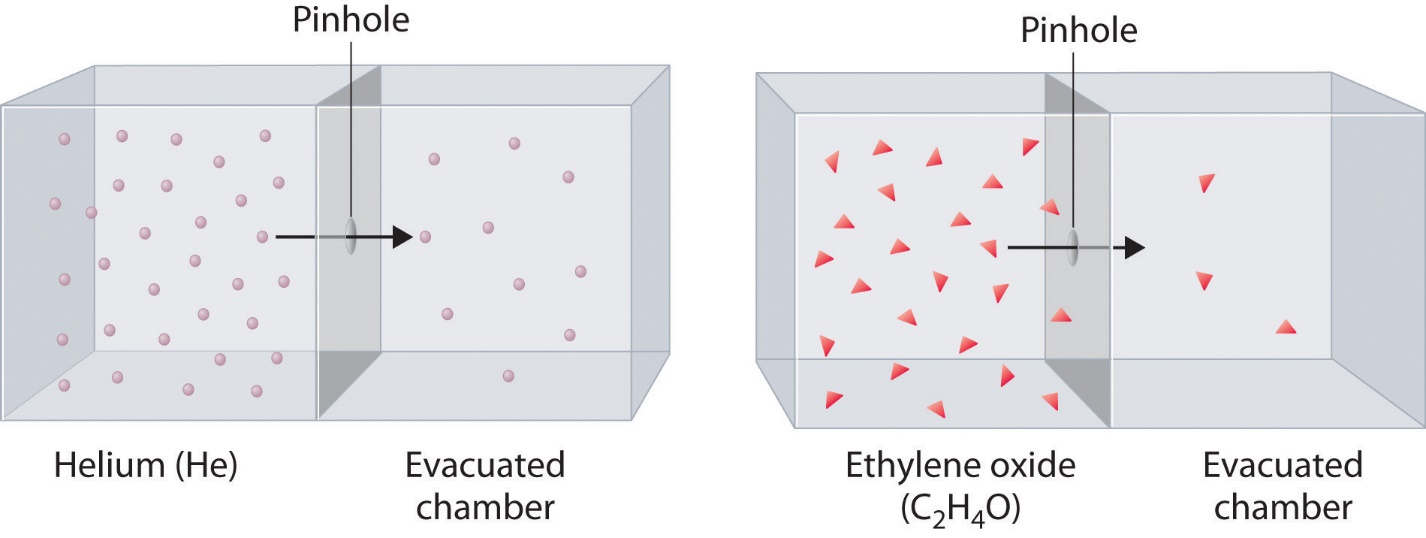
Figure 2.7.3. Les atomes He plus légers (M = 4,00 g/mole) s’écoulent par le petit trou plus rapidement que les molécules d’oxyde d’éthylène (C2H4O) plus lourdes (M = 44,0 g/mole), comme le prédit la loi de Graham.
La théorie cinétique et moléculaire explique le comportement des gaz, partie II
Selon la loi de Graham (dont il sera question plus loin dans cette section), les molécules d’un gaz sont en mouvement rapide et les molécules elles-mêmes sont petites. La distance moyenne entre les molécules d’un gaz est grande par rapport à la taille des molécules. En conséquence, les molécules de gaz peuvent se déplacer facilement les unes par rapport aux autres et se diffuser à des vitesses relativement rapides. La vitesse d’effusion d’un gaz dépend directement de la vitesse (moyenne) de ses molécules :
effusion ∝ urms
En utilisant cette relation, et l’équation reliant la vitesse moléculaire à la masse, la loi de Graham peut être facilement dérivée comme montré ici :
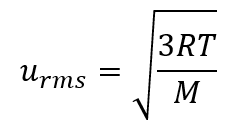
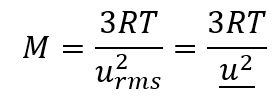
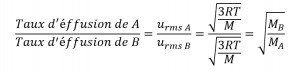
Le rapport des taux d’éffusion est donc inversement proportionnel au rapport des racines carrées de leurs masses. C’est la même relation observée expérimentalement et exprimée par la loi de Graham. Regardez cette vidéo pour mieux visualiser les taux d’effusion.
Exemple 2.7.1 – Application de la loi de Graham aux taux d’effusion
Calculer le rapport entre la vitesse d’effusion de l’hydrogène et la vitesse d’effusion de l’oxygène, en utilisant a) les masses molaires ; et b) les densités de gaz.
Solution
Utilisation de la loi de Graham et application des masses molaires :
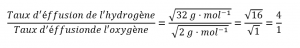
Les densités de l’oxygène et de l’hydrogène à la STP sont respectivement de 1,43 g/L et 0,0899 g/L. En recalculant la loi de Graham avec les densités, on obtient un résultat numérique identique :
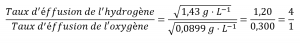
L’hydrogène s’écoule quatre fois plus vite que l’oxygène.
Vérifiez votre apprentissage 2.7.1 – Application de la loi de Graham aux taux d’effusion
À une pression et température donnée, l’azote gazeux s’échappe à un taux de 79 mL/s. En utilisant le même appareil à la même température et à la même pression, à quelle vitesse le dioxyde de soufre s’effuse ?
Réponse
52 mL/s
Voici un autre exemple, qui montre en quoi les temps déterminants diffèrent des taux déterminants.
Exemple 2.7.2 – Calculs du temps d’effusion
Il faut 243 s pour que 4,46 × 10-5 mol Xe s’écoulent par un minuscule trou. Dans les mêmes conditions, combien de temps faudra-t-il pour que 4,46 × 10-5 mol Ne s’effuse ?
Solution
Il est important de résister à la tentation d’utiliser directement les temps, et de se rappeler comment le taux est lié au temps aussi bien qu’à la masse. Rappelez-vous la définition de la vitesse effusion :
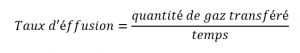
et le combiner avec la loi de Graham :

Pour obtenir :

Noter que la quantité de A = quantité de B, et résoudre pour le temps pour Ne :
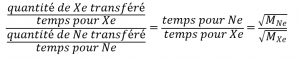
et des valeurs de substitution :
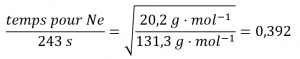
Enfin, résolvez pour la quantité désirée :
temps pour Ne = 0,392 x 243 s = 95,3 s
Notez que cette réponse est raisonnable : Comme Ne est plus léger que Xe, le taux d’effusion de Ne sera plus important que celui de Xe, ce qui signifie que le temps d’effusion de Ne sera plus court que celui de Xe.
Vérifiez votre apprentissage 2.7.2 – Calculs du temps d’effusion
Un ballon de fête rempli d’hélium se dégonfle pour 2/3 de son volume original en 8,0 heures. Combien de temps faudra-t-il à un ballon identique rempli du même nombre de moles d’air (Mm = 28,2 g/mol) pour se dégonfler à 1/2 de son volume original ?
Réponse
32 h
Enfin, voici un autre exemple montrant comment calculer la masse molaire à partir de données sur le taux d’effusion.
Exemple 2.7.3 – Déterminer la masse molaire à l’aide de la loi de Graham
Un gaz inconnu s’échappe environ 1,21 fois plus rapidement que le CO2. Quelle est la masse molaire du gaz inconnu ? Parmi les 5 gaz suivants, lequel correspond le mieux à l’identité du gaz inconnu ?
Ne NO CH4 C3H8 SO2
Solution
De la loi de Graham, nous avons :
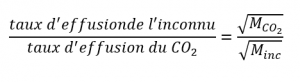
Branchez les données connues :
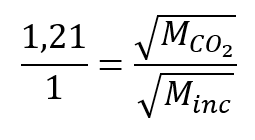
Résoudre :
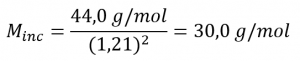
Les masses molaires des cinq composés gazeux répertoriés sont :
Ne CH4 NO C3H8 SO2
20,18 g/mol 16,04 g/mol 30,01 g/mol 44,09 g/mol 64,06 g/mol
Parmi les cinq composés, le NO, également appelé monoxyde d’azote, a une masse molaire de 30,01 g/mole. Par conséquent, parmi les choix proposés, le gaz est le NO.
Vérifiez votre apprentissage 2.7.3 – Déterminer la masse molaire à l’aide de la loi de Graham
L’hydrogène gazeux s’échappe à travers un récipient poreux 8,97 fois plus vite qu’un gaz inconnu. Estimez la masse molaire du gaz inconnu.
Réponse
163 g/mol
|
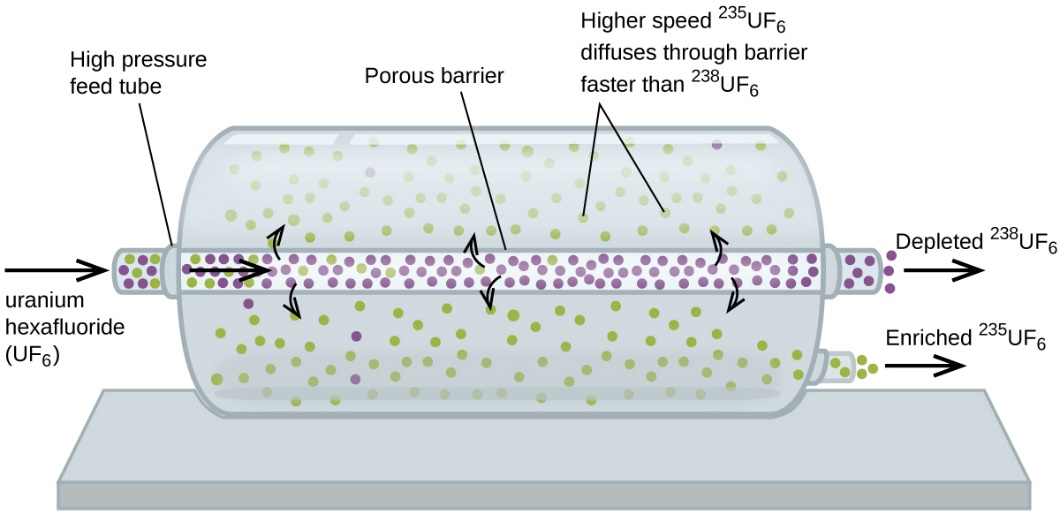
Au cas où vous seriez intéressé… Utilisation de la diffusion pour des applications dans le domaine de l’énergie nucléaire : Enrichissement de l’uranium |
|
La diffusion gazeuse a été utilisée pour produire de l’uranium enrichi destiné aux centrales nucléaires et aux armes. L’uranium naturel ne contient que 0,72% de 235U, le type d’uranium « fissile », c’est-à-dire capable d’entretenir une réaction de fission nucléaire en chaîne. Les réacteurs nucléaires ont besoin d’un combustible contenant 2 à 5 % de 235U, et les bombes nucléaires ont besoin de concentrations encore plus élevées. Une façon d’enrichir l’uranium aux niveaux souhaités est de tirer parti de la loi de Graham. Dans une usine d’enrichissement par diffusion gazeuse, l’hexafluorure d’uranium (UF6, le seul composé d’uranium suffisamment volatil pour fonctionner) est lentement pompé à travers de grandes cuves cylindriques appelées diffuseurs, qui contiennent des barrières poreuses avec des ouvertures microscopiques. Il s’agit d’un processus de diffusion car l’autre côté de la barrière n’est pas évacué. Les molécules de 235UF6 ont une vitesse moyenne plus élevée et diffusent à travers la barrière un peu plus vite que les molécules plus lourdes de 238UF6. Le gaz qui a traversé la barrière est donc légèrement enrichi en 235UF6 et le gaz résiduel est légèrement appauvri. La faible différence de poids moléculaire entre le 235UF6 et le 238UF6 n’entraîne qu’un enrichissement d’environ 0,4 % par diffuseur (figure 2.7.4). Mais en connectant plusieurs diffuseurs dans une séquence d’étapes (appelée cascade), le niveau d’enrichissement souhaité peut être atteint.
Figure 2.7.4. Dans un diffuseur, l’UF6 gazeux est pompé à travers une barrière poreuse qui sépare partiellement le 235UF6 du 238UF6. L’UF6 doit passer à travers de nombreuses grandes unités de diffusion pour obtenir un enrichissement suffisant en 235U. La séparation à grande échelle des gaz 235UF6 et 238UF6 a été réalisée pour la première fois pendant la Seconde Guerre mondiale, à l’installation d’énergie atomique d’Oak Ridge, Tennessee, dans le cadre du projet Manhattan (développement de la première bombe atomique). Bien que la théorie soit simple, il a fallu surmonter de nombreux défis techniques de taille pour la mettre en pratique. La barrière doit avoir des trous minuscules et uniformes (environ 10-6 cm de diamètre) et être suffisamment poreuse pour produire des débits élevés. Tous les matériaux (la barrière, les tubes, les revêtements de surface, les lubrifiants et les joints) doivent pouvoir contenir l’UF6, hautement réactif et corrosif, mais ne doivent pas réagir avec lui. Comme les installations de diffusion gazeuse nécessitent de très grandes quantités d’énergie (pour comprimer le gaz aux pressions élevées requises et le faire passer à travers la cascade de diffuseurs, pour éliminer la chaleur produite lors de la compression, etc. |
Questions
★ Questions
1. Un ballon rempli d’hélium prend 6 heures pour se dégonfler à 50 % de son volume initial. Combien de temps faudra-t-il (temps) pour qu’un ballon identique rempli du même volume de gaz hydrogène (au lieu d’hélium) diminue son volume de 50% (en heures) ?
2. Expliquez pourquoi les nombres de molécules ne sont pas identiques dans les ampoules de gauche et de droite de l’illustration centrale de la figure 2.7.1.
3. En commençant par la définition de la vitesse d’effusion et la découverte de Graham mettant en relation la vitesse et la masse molaire, montrez comment dériver l’équation de la loi de Graham, mettant en relation les vitesses relatives d’effusion de deux gaz avec leurs masses moléculaires.
4. L’eau lourde, D2O (masse molaire = 20,03 g mol-1), peut être séparée de l’eau ordinaire, H2O (masse molaire = 18,01), en raison de la différence des vitesses relatives de diffusion des molécules dans la phase gazeuse. Calculer les taux de diffusion relatifs de H2O et de D2O.
5. Parmi les gaz suivants, lequel se diffuse plus lentement que l’oxygène ? F2, Ne, N2O, C2H2, NO, Cl2, H2S
★★ Questions
6. Lors de la discussion sur la diffusion gazeuse pour l’enrichissement de l’uranium, il a été affirmé que le 235UF6 diffuse 0,4% plus vite que le 238UF6. Montrez le calcul qui soutient cette valeur. La masse molaire du 235UF6 = 235,043930 + 6 × 18,998403 = 349,034348 g/mol, et la masse molaire du 238UF6 = 238,050788 + 6 × 18,998403 = 352,041206 g/mol.
7. Calculer la vitesse de diffusion relative de 1H2 (masse molaire 2,0 g/mol) par rapport à celle de 2H2 (masse molaire 4,0 g/mol) et la vitesse de diffusion relative de O2 (masse molaire 32 g/mol) par rapport à celle de O3 (masse molaire 48 g/mol).
8. Un gaz d’identité inconnue se diffuse à un taux de 83,3 mL/s dans un appareil de diffusion dans lequel le dioxyde de carbone se diffuse à un taux de 102 mL/s. Calculer la masse moléculaire (g⋅mol-1) du gaz inconnu.
9. Lorsque deux bouchons de coton, l’un humidifié à l’ammoniac et l’autre à l’acide chlorhydrique, sont simultanément insérés dans les extrémités opposées d’un tube de verre de 87,0 cm de long, un anneau blanc de NH4Cl se forme là où le NH3 gazeux et le HCl gazeux entrent en contact pour la première fois.
NH3 (g) + HCl (g) ⟶ NH4Cl (s)
À quelle distance approximative du bouchon humidifié à l’ammoniac cela se produit-il ? (Conseil : calculez les taux de diffusion du NH3 et du HCl, et découvrez à quelle vitesse le NH3 diffuse plus rapidement que le HCl).
Réponses
1. 4,2 heures
2. Dans la figure centrale, on voit qu’il y a plus de H2 présent du côté droit que du côté gauche. Cela s’explique par le taux d’épanchement. L’H2 a un taux d’effusion plus rapide que l’O2 car il a une masse moléculaire plus petite. Cela signifie que H2 passera à travers le trou à un rythme plus rapide que O2, ce qui crée cette distribution inégale des particules comme le montre la figure 2.7.1.
3. L’effusion peut être définie comme le processus par lequel un gaz s’échappe par un trou d’épingle dans un vide. La loi de Graham stipule qu’avec un mélange de deux gaz A et B :![]() . A et B se trouvent tous deux dans le même récipient à la même température et auront donc la même énergie cinétique :
. A et B se trouvent tous deux dans le même récipient à la même température et auront donc la même énergie cinétique :
![]()
Par conséquent,
![]()
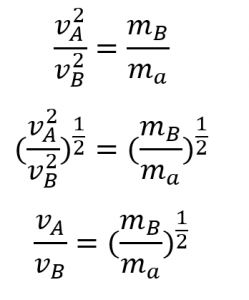
4. ![]()
5. F2, N2O, Cl2, H2S
6.
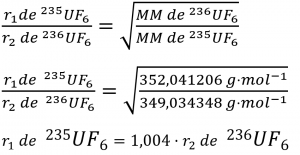
7. 1.4 ; 1.2
8. 65,99 g mol-1
9. 51,7 cm
Distance moyenne parcourue par une molécule entre deux collisions
Mouvement d'un atome ou d'une molécule d'une région de concentration relativement élevée à une région de concentration relativement faible (discuté au chapitre 2 en ce qui concerne les espèces gazeuses, mais applicable aux espèces de toute phase)
Quantité de gaz se diffusant à travers une zone donnée pendant un temps donné
Transfert d'atomes ou de molécules gazeuses d'un récipient vers un vide par de très petites ouvertures
Les taux de diffusion et d'effusion des gaz sont inversement proportionnels aux racines carrées de leurs masses moléculaires