2.6 – Théorie cinétique moléculaire (comportements des gaz idéaux)
Les lois du gaz que nous avons vues jusqu’à présent, ainsi que l’équation du gaz idéal, sont empiriques, c’est-à-dire qu’elles ont été dérivées d’observations expérimentales. Les formes mathématiques de ces lois décrivent étroitement le comportement macroscopique de la plupart des gaz à basse pression (c’est-à-dire moins de 1 ou 2 atm). Bien que les lois des gaz décrivent des relations qui ont été vérifiées par de nombreuses expériences, elles ne nous disent pas pourquoi les gaz suivent ces relations.
La théorie cinétique moléculaire (TCM) est un modèle microscopique simple qui explique efficacement les lois des gaz décrites dans les modules précédents de ce chapitre. Cette théorie est basée sur les cinq postulats suivants décrits ici. (Remarque : le terme « molécule » sera utilisé pour désigner les différentes espèces chimiques qui composent le gaz, bien que certains gaz soient composés d’espèces atomiques, par exemple, les gaz rares).
- Les gaz sont composés de molécules qui sont en mouvement continu, se déplaçant en ligne droite et changeant de direction uniquement lorsqu’elles entrent en collision avec d’autres molécules ou avec les parois d’un récipient.
- Les molécules qui composent le gaz sont négligeables par rapport aux distances qui les séparent.
- La pression exercée par un gaz dans un récipient résulte des collisions entre les molécules de gaz et les parois du récipient.
- Les molécules de gaz n’exercent aucune force d’attraction ou de répulsion les unes sur les autres ou sur les parois du récipient ; leurs collisions sont donc élastiques (n’entraînent pas de perte d’énergie).
- L’énergie cinétique moyenne des molécules de gaz est proportionnelle à la température kelvin du gaz.
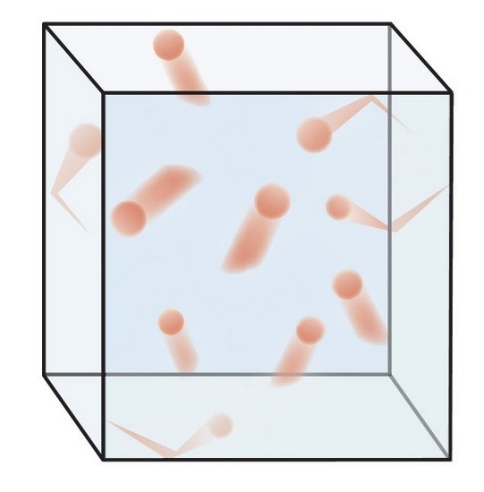
Figure 2.6.1. Visualisation du mouvement moléculaire. Les molécules d’un gaz sont en mouvement constant et entrent en collision les unes avec les autres et avec la paroi du récipient.
Le test du TCM et de ses postulats est sa capacité à expliquer et à décrire le comportement d’un gaz. Les différentes lois des gaz peuvent être dérivées des postulats du TCM, ce qui a conduit les chimistes à penser que les hypothèses de la théorie représentent avec précision les propriétés des molécules de gaz. Nous allons d’abord examiner les différentes lois des gaz (lois de Boyle, Charles, Amontons, Avogadro et Dalton) d’un point de vue conceptuel pour voir comment le TCM les explique. Ensuite, nous examinerons plus attentivement les relations entre les masses moléculaires, les vitesses et les énergies cinétiques et la température, et nous expliquerons la loi de Graham.
La théorie cinétique et moléculaire explique le comportement des gaz, partie I
En rappelant que la pression du gaz est exercée par des molécules de gaz en mouvement rapide et dépend directement du nombre de molécules frappant une unité de surface de la paroi par unité de temps, on voit que la TCM explique conceptuellement le comportement d’un gaz comme suit :
- La loi Amontons / Gay-Lussac. Si la température est augmentée, la vitesse moyenne et l’énergie cinétique des molécules de gaz augmentent. Si le volume est maintenu constant, l’augmentation de la vitesse des molécules de gaz entraîne des collisions plus fréquentes et plus violentes avec les parois du récipient, ce qui augmente la pression (figure 2.6.2(a)).
- La loi de Charles. Si la température d’un gaz est augmentée, une pression constante ne peut être maintenue que si le volume occupé par le gaz augmente. Cela entraînera une augmentation des distances moyennes parcourues par les molécules pour atteindre les parois du récipient, ainsi qu’une augmentation de la surface des parois. Ces conditions réduiront à la fois la fréquence des collisions entre les parois des molécules et le nombre de collisions par unité de surface, dont les effets combinés compensent l’effet des forces de collision accrues dues à l’énergie cinétique plus importante à la température plus élevée.
- La loi de Boyle. Si le volume de gaz diminue, la surface de la paroi du réservoir diminue et la fréquence de collision entre les parois des molécules augmente, ce qui augmente la pression exercée par le gaz (figure 2.6.2(b)).
- La loi d’Avogadro. À pression et température constantes, la fréquence et la force des collisions entre les parois des molécules sont constantes. Dans de telles conditions, l’augmentation du nombre de molécules gazeuses nécessitera une augmentation proportionnelle du volume du récipient afin d’obtenir une diminution du nombre de collisions par unité de surface pour compenser la fréquence accrue des collisions (figure 2.6.2(c)).
- La loi Dalton. En raison des grandes distances qui les séparent, les molécules d’un gaz dans un mélange bombardent les parois du récipient avec la même fréquence, que d’autres gaz soient présents ou non, et la pression totale d’un mélange de gaz est égale à la somme des pressions (partielles) des différents gaz.
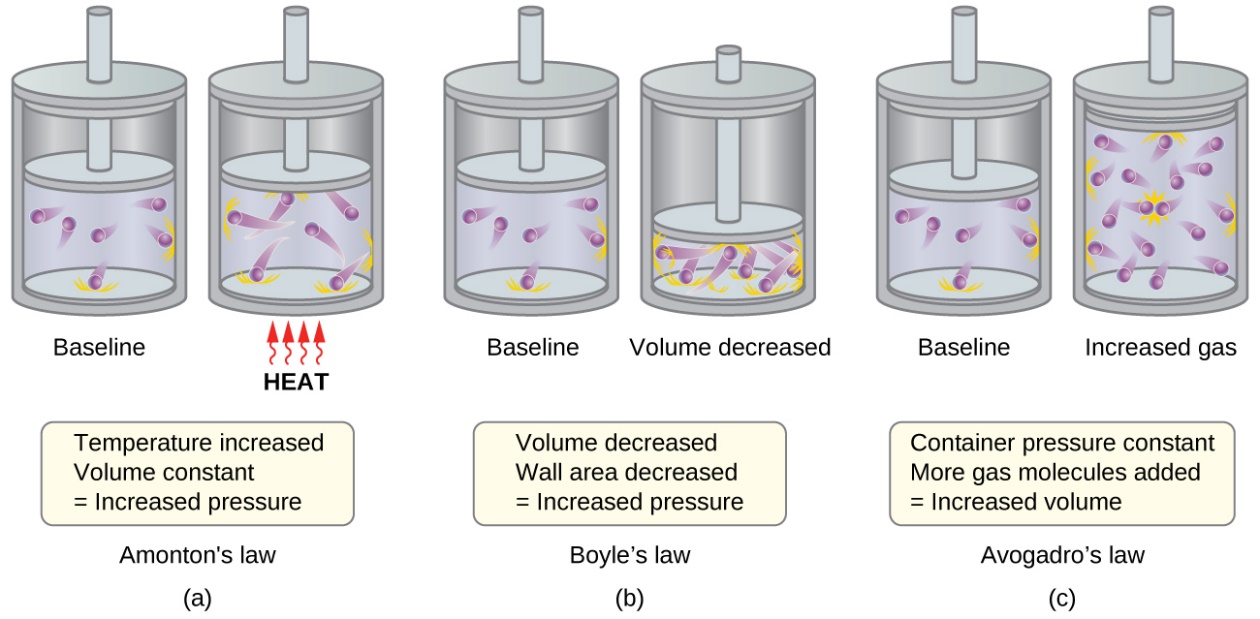
Figure 2.6.2. (a) Lorsque la température du gaz augmente, la pression du gaz augmente en raison de l’augmentation de la force et de la fréquence des collisions moléculaires. (b) Lorsque le volume diminue, la pression du gaz augmente en raison de la fréquence accrue des collisions moléculaires. (c) Lorsque la quantité de gaz augmente à une pression constante, le volume augmente pour donner un nombre constant de collisions par unité de surface de paroi par unité de temps.
Vitesses moléculaires et énergie cinétique
La discussion précédente a montré que le TCM explique qualitativement les comportements décrits par les différentes lois sur les gaz. Les postulats de cette théorie peuvent être appliqués de manière plus quantitative pour dériver ces lois individuelles. Pour ce faire, nous devons d’abord examiner les vitesses et les énergies cinétiques des molécules de gaz, ainsi que la température d’un échantillon de gaz.
Dans un échantillon de gaz, les molécules individuelles ont des vitesses très variables ; cependant, en raison du grand nombre de molécules et de collisions impliquées, la distribution de la vitesse moléculaire et la vitesse moyenne sont constantes. Cette distribution de la vitesse moléculaire est connue sous le nom de distribution de Maxwell-Boltzmann, et elle représente le nombre relatif de molécules dans un échantillon de gaz en vrac qui possède une vitesse donnée (figure 2.6.3.).
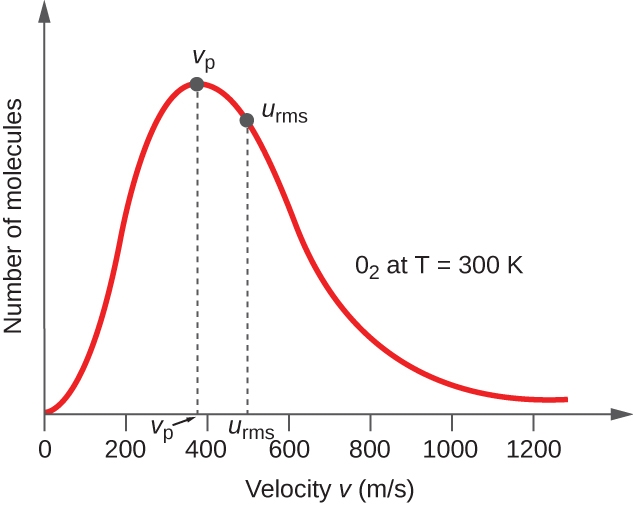
Figure 2.6.3. La distribution de la vitesse moléculaire de l’oxygène gazeux à 300 K est illustrée ici. Très peu de molécules se déplacent à des vitesses très faibles ou très élevées. Le nombre de molécules ayant des vitesses intermédiaires augmente rapidement jusqu’à un maximum, qui est la vitesse la plus probable, puis diminue rapidement. Notez que la vitesse la plus probable, νp, est d’un peu moins de 400 m/s, tandis que la vitesse moyenne quadratique, urms, est plus proche de 500 m/s.
L’énergie cinétique (Ek) d’une particule de masse (m) et de vitesse (u) est donnée par :
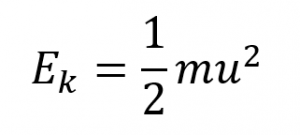
Équation 2.6.1 Énergie cinétique par rapport à la vitesse et à la masse
En exprimant la masse en kilogrammes et la vitesse en mètres par seconde, on obtient des valeurs énergétiques en unités de joules (J = kg m2 s-2). Pour traiter une grande population de molécules de gaz, nous utilisons des moyennes à la fois pour la vitesse et l’énergie cinétique. Dans le TCM, la vitesse moyenne quadratique d’une particule, urms, est définie comme la racine carrée de la moyenne des carrés des vitesses avec n = le nombre de particules :
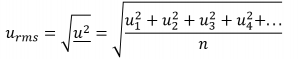
Équation 2.6.2 Moyenne quadratique d’une particule
Notez que cette valeur est mathématiquement différente de la moyenne arithmétique de la population de gaz, et ne correspond pas non plus à la vitesse moléculaire la plus probable (vp).
L’énergie cinétique moyenne pour une mole de particules, Ek moy, est alors égale à (où M est la masse moyenne des particules, exprimée en kilogrammes) :
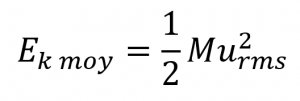
Équation 2.6.3 Énergie cinétique moyenne d’une mole de particules
L’Ek moy d‘une mole de molécules de gaz est également directement proportionnelle à la température du gaz et peut être décrite par l’équation (pour étendre votre apprentissage, consultez la dérivation de l’Ek moy ici) :
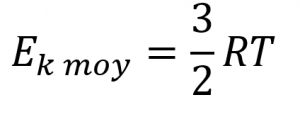
Équation 2.6.4 Énergie cinétique moyenne par rapport à la température
où R est la constante du gaz et T la température kelvin. Lorsqu’elle est utilisée dans cette équation, la forme appropriée de la constante de gaz est 8,314 J/mol⋅K (8,314 kg m2 s-2 mol-1 K-1). Ces deux équations distinctes pour Ek moy peuvent être combinées et réorganisées pour obtenir une relation entre la vitesse moléculaire et la température :
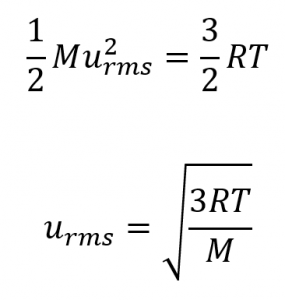
Équation 2.6.5 Vitesse moléculaire en fonction de la température
Exemple 2.6.1 – Calcul des urms
Calculer la vitesse moyenne quadratique d’une molécule d’azote à 30 °C.
Solution
Convertissez la température en Kelvin :
30 ∘C + 273 = 303 K
Déterminez la masse molaire de l’azote en kilogrammes :
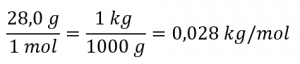
Remplacer les variables et les constantes dans l’équation de la vitesse moyenne quadratique, en remplaçant les Joules par l’équivalent en kg m2 s-2 :
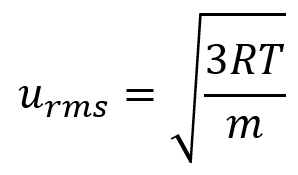
Vérifiez votre apprentissage 2.6.1 – Calcul des urms
Calculer la vitesse moyenne quadratique d’une mole de molécules d’oxygène à -23 °C.
Réponse
441 m/s
Si la température d’un gaz augmente, son Ek moy augmente, plus de molécules ont des vitesses plus élevées et moins de molécules ont des vitesses plus faibles, et la distribution s’étend vers des vitesses plus élevées dans l’ensemble, c’est-à-dire vers la droite (notez que la courbe passe toujours par l’origine, ce qui signifie qu’il y a toujours quelques particules qui se déplacent lentement). Si la température diminue, Ek moy diminue, plus de molécules ont une vitesse plus faible et moins de molécules ont une vitesse plus élevée, et la distribution se déplace vers des vitesses plus faibles dans l’ensemble, c’est-à-dire vers la gauche. Ce comportement est illustré pour l’azote gazeux dans la figure 2.6.4.
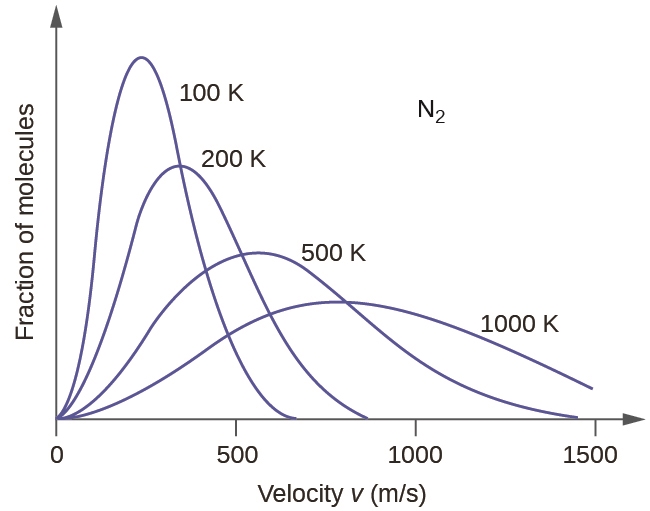
Figure 2.6.4. La distribution de la vitesse moléculaire de l’azote gazeux (N2) se déplace vers la droite et s’aplatit lorsque la température augmente ; elle se déplace vers la gauche et s’accentue lorsque la température diminue.
À une température donnée, tous les gaz ont la même Ek moy pour leurs molécules. Les gaz composés de molécules plus légères ont plus de particules à grande vitesse et donc un plus grand nombre d’urms, avec une distribution de vitesse qui atteint son maximum à des vitesses relativement plus élevées. Les gaz composés de molécules plus lourdes ont plus de particules à faible vitesse, donc un nombre d’urms plus faible, et une distribution de vitesse qui culmine à des vitesses relativement plus faibles. Cette tendance est démontrée par les données relatives à une série de gaz rares présentées à la figure 2.6.5.
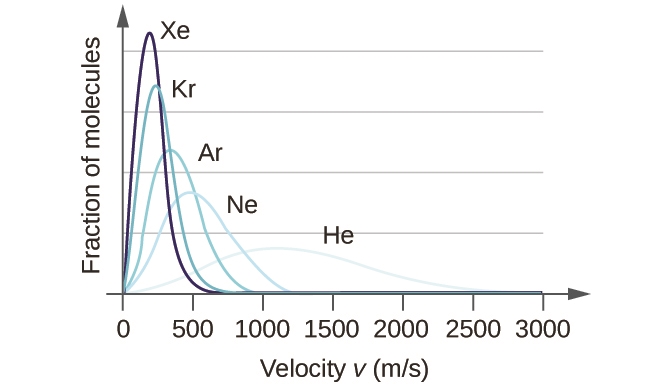
Figure 2.6.5. La vitesse moléculaire est directement liée à la masse moléculaire. À une température donnée, les molécules légères se déplacent en moyenne plus vite que les molécules lourdes.
Le simulateur de gaz peut être utilisé pour examiner l’effet de la température sur les vitesses moléculaires. Examinez les « histogrammes d’énergie » (distributions des vitesses moléculaires) et les « informations sur les espèces » (qui donnent les valeurs moyennes des vitesses) du simulateur pour des molécules de différentes masses à différentes températures.
Questions
★ Questions
1. En utilisant les postulats de la théorie moléculaire cinétique, expliquez pourquoi un gaz remplit uniformément un récipient de n’importe quelle forme.
2. La vitesse d’une molécule donnée dans un gaz peut-elle doubler à température constante? Expliquez votre réponse.
3. Décrivez ce qui arrive à l’énergie cinétique moyenne des molécules de gaz idéal lorsque les conditions sont modifiées comme suit :
a. La pression du gaz est augmentée en réduisant le volume à température constante.
b. La pression du gaz est augmentée en augmentant la température à volume constant.
c. La vitesse moyenne des molécules est multipliée par 2.
4. Quel est le rapport entre l’énergie cinétique moyenne d’une molécule de SO2 et celle d’une molécule d’O2 dans un mélange de deux gaz ? Quel est le rapport des vitesses moyennes quadratiques, urms, des deux gaz ?
5. Un échantillon de 1 L de CO initialement à la STP est chauffé à 546 K, et son volume est porté à 2 L.
a. Quel effet ces changements ont-ils sur le nombre de collisions des molécules du gaz par unité de surface de la paroi du récipient ?
b. Quel est l’effet sur l’énergie cinétique moyenne des molécules ?
c. Quel est l’effet sur la vitesse moyenne quadratique des molécules ?
6. La vitesse moyenne quadratique des molécules de H2 à 25 °C est d’environ 1,6 km/s. Quelle est la vitesse moyenne quadratique d’une molécule de N2 à 25 °C ?
★★ Questions
7. Répondez aux questions suivantes sur une montgolfière :
a. La pression du gaz dans la montgolfière indiquée à l’ouverture de ce chapitre est-elle supérieure, inférieure ou égale à celle de l’atmosphère à l’extérieur de la montgolfière ?
b. La densité du gaz dans la montgolfière indiquée à l’ouverture de ce chapitre est-elle supérieure, inférieure ou égale à celle de l’atmosphère à l’extérieur du ballon ?
c. À une pression de 1 atm et une température de 20 °C, l’air sec a une densité de 1,2256 g/L. Quelle est la masse molaire (moyenne) de l’air sec?
d. La température moyenne du gaz dans une montgolfière est de 1,30 × 102 °F. Calculez sa densité, en supposant que la masse molaire est égale à celle de l’air sec.
e. La capacité de levage d’un ballon à air chaud est égale à la différence entre la masse de l’air froid déplacé par le ballon et la masse du gaz dans le ballon. Quelle est la différence entre la masse de 1,00 L d’air froid dans la partie (c) et la masse d’air chaud dans la partie (d)?
f. Un ballon moyen a un diamètre de 60 pieds et un volume de 1,1 × 105 pieds3. Quelle est la puissance de levage d’un tel ballon? Si le poids du ballon et de son fret est de 500 livres, quelle est sa capacité à transporter des passagers et du fret?
g. Un ballon transporte 40,0 gallons de propane liquide (densité 0,5005 g/L). Quel volume de gaz CO2 et H2O est produit par la combustion de ce propane ?
h. Un vol en montgolfière peut durer environ 90 minutes. Si tout le carburant est brûlé pendant ce temps, quel est le taux approximatif de perte de chaleur (en kJ/min) de l’air chaud dans le sac pendant le vol ?
8. Montrer que le rapport entre la vitesse de diffusion du gaz 1 et la vitesse de diffusion du gaz 2, R1/R2 ,est la même à 0 °C et à 100 °C.
Réponses
1. Les gaz sont composés de molécules qui sont en mouvement continu, voyageant en ligne droite et ne déviant qu’une fois en collision avec d’autres molécules. La pression exercée par un gaz dans un récipient résulte des collisions entre les molécules de gaz et les parois. Les molécules de gaz sont de taille négligeable par rapport aux distances qui les séparent.
2. Oui. À tout instant, il existe une gamme de valeurs de vitesses moléculaires dans un échantillon de gaz. Une seule molécule peut accélérer ou ralentir lorsqu’elle entre en collision avec d’autres molécules. La vitesse moyenne de toutes les molécules est constante à température constante.
3. (a) l’énergie cinétique moyenne reste inchangée, (b) l’augmentation de P entraîne une augmentation de l’énergie cinétique moyenne, (c) le doublement de la vitesse entraîne un quadruplement de l’énergie cinétique
4. (a) Le rapport des énergies cinétiques moyennes est de 1, (b) 0,71
5. (a) Le nombre de collisions par unité de surface de la paroi du contenant est constant. (b) L’énergie cinétique moyenne double. (c) La vitesse quadratique moyenne augmente à √2 fois sa valeur initiale ; l’urms est proportionnelle à √Ekmoy.
6. (a) 1,92 km/s
7. (a) égal ; (b) inférieur à ; (c) 29,48 g mol-1 ; (d) 1,0966 g L-1 ; (e) 0,129 g/L ; (f) 4,01 × 105 g ; capacité de levage nette = 384 lb ; (g) 270 L ; (h) 39,1 kJ min-1
8. ![]()
9. Dans l’hypothèse d’un système de gaz 1 et de gaz 2 avec des masses m1 et m2, la vitesse de diffusion dépend uniquement de la masse et non de la température. Par conséquent, la vitesse de diffusion restera constante à différentes températures.
Théorie basée sur des principes et des hypothèses simples qui explique efficacement le comportement idéal des gaz en nous aidant à comprendre les gaz au niveau moléculaire et leurs propriétés physiques
Mesure de la vitesse moyenne pour un groupe de particules calculée comme la racine carrée de la vitesse moyenne au carré

