2.3 – La mesure des variables des gaz

Pression

Tout objet, que ce soit votre ordinateur, une personne ou un échantillon de gaz, exerce une force sur toute surface avec laquelle il entre en contact. L’air dans un ballon, par exemple, exerce une force contre la surface intérieure du ballon, et un liquide injecté dans un moule exerce une force contre la surface intérieure du moule, tout comme une chaise exerce une force contre le sol en raison de sa masse et des effets de la gravité. Si l’air d’un ballon est chauffé, l’énergie cinétique accrue du gaz finit par faire éclater le ballon en raison de la pression accrue (P) du gaz, la force (F) par unité de surface (A) de la surface :

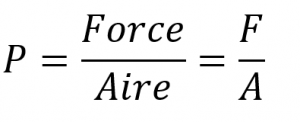
Équation 2.3.1 Relation entre la force de pression et l’aire ou surface

La pression dépend à la fois de la force exercée et de l’aire de la zone sur laquelle la force est appliquée. Nous savons, grâce à l’équation reliant la force, la surface et la pression, que l’application de la même force sur une surface plus petite produit une pression plus élevée. Lorsque nous utilisons un tuyau pour laver une voiture, par exemple, nous pouvons augmenter la pression de l’eau en réduisant la taille de l’ouverture du tuyau avec un pouce.

Les unités de pression sont dérivées des unités utilisées pour mesurer la force et la surface. L’unité SI de pression, dérivée des unités SI de force (newtons) et de surface (mètres carrés), est le newton par mètre carré (N/m²), appelé le Pascal (Pa), du nom du mathématicien français Blaise Pascal (1623 – 1662) :

1 Pa = 1 N/m²

Un pascal est une très petite pression ; dans de nombreux cas, il est plus pratique d’utiliser des unités de kilopascal (1 kPa = 1000 Pa) ou de barre (1 bar = 100 000 Pa).

Exemple 2.3.1 – La pression exercée par un livre de poche

En supposant qu’un livre de poche ait une masse de 2,00 kg, une longueur de 27,0 cm, une largeur de 21,0 cm et une épaisseur de 4,5 cm, quelle pression exerce-t-il sur une surface si c’est le cas :

1. À plat?

2. Sur le côté dans une bibliothèque?

Solution

La force exercée par le livre ne dépend pas de son orientation. Rappelons que la force exercée par un objet est F = ma, où m est sa masse et a son accélération. Dans le champ gravitationnel de la Terre, l’accélération est due à la gravité (9,8067 m/s² à la surface de la Terre). En unités SI, la force exercée par le livre est donc :

Nous avons calculé la force comme étant de 19,6 N. Lorsque le livre est posé à plat, la surface est :

A = 0,270 m × 0,210 m = 0,0567 m²

Si le livre se trouve à son extrémité ou sur son côté, la force reste la même, mais la surface diminue :

A = 21,0 cm × 4,5 cm = 0,210 m × 0,045 m = 9,5 × 10^-3 m²

B) La pression exercée par le texte à plat est donc :

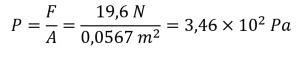
La pression exercée par le texte qui se trouve à son extrémité l’est donc :

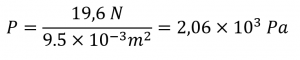
Vérifiez votre apprentissage 2.3.2 – La pression exercée par un livre de poche

Quelle pression un étudiant de 60,0 kg exerce-t-il sur le sol :

a. Lorsqu’il se tient à plat pieds dans le laboratoire dans une paire de chaussures de tennis (la surface des semelles est d’environ 180 cm²) ?

b. Alors qu’elle marche le talon en premier sur une piste de danse avec des chaussures à talons hauts (la surface du talon = 1,0 cm²) ?

Réponse

a. 3,27 × 10⁴ Pa

b. 5,9 × 10⁶ Pa

Pression atmosphérique

L’air qui entoure la terre est tiré vers la surface par la gravité de la même manière que le livre de poche dans l’exemple ci-dessus. Par conséquent, l’air exerce également une pression sur la surface. C’est ce qu’on appelle la pression atmosphérique.

La vidéo suivante montre la “puissance” de la pression atmosphérique. Une boîte métallique remplie d’eau est chauffée jusqu’à ce que l’eau à l’intérieur bout, créant ainsi une pression interne élevée. La boîte est ensuite placée à l’envers dans un bol d’eau glacée froide, ce qui provoque le refroidissement et la diminution du volume de la vapeur d’eau autrefois chaude. Ce refroidissement entraîne une diminution de la pression interne de la boîte. La pression plus basse exerce moins de force sur la canette et ne peut plus contrer la pression atmosphérique provenant de l’extérieur de la canette, qui pousse vers l’intérieur, écrasant la canette. On peut également le voir sur la figure 2.3.1. à une échelle beaucoup plus grande.

Figure 2.3.1. Thomas le wagon-citerne est écrasé par la différence de pression.

Comme les vents peuvent ajouter de l’air ou en enlever de la colonne verticale au-dessus d’une zone donnée de la surface, la pression atmosphérique varie. La pression diminue également lorsque l’on se déplace vers des altitudes plus élevées. Les sommets de l’Himalaya, les plus hautes montagnes du monde à environ 8000 m (presque 5 miles), sont au-dessus de plus de la moitié de l’atmosphère. La pression plus basse à ces hauteurs rend la respiration très difficile – même le moindre effort laisse une personne haletante et faible. C’est pourquoi les avions à réaction, qui volent régulièrement à des altitudes de 8 à 10 km, sont équipés pour maintenir artificiellement la pression de l’air dans leur cabine.

Il est souvent pratique d’exprimer la pression en utilisant une unité qui est à peu près la même que la pression atmosphérique moyenne au niveau de la mer. Comme nous l’avons vu dans l’exemple 1, la pression atmosphérique est d’environ 101 kPa, et l’atmosphère standard (atm) est définie comme étant exactement 101,325 kPa. Comme cette unité est souvent utilisée, il est utile de rappeler que :

Exemple 2.3.3 – Pression atmosphérique

La masse totale d’air directement au-dessus d’une section de 30 cm sur 140 cm de l’océan Atlantique était de 4,34 × 10³ kg le 27 juillet 1977. Calculer la pression exercée à la surface de l’eau par l’atmosphère.

Solution

Calculer d’abord la force d’attraction gravitationnelle sur l’air

F = ma = (4.34 × 10³ kg) × (9.81 m⋅s^-2) = 4.26 × 10⁴ kg⋅m⋅s^-2 = 4.26 × 10⁴ N

L’aire de la surface est

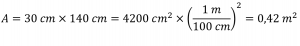
Ainsi, la pression est

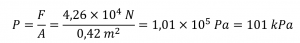
Pression barométrique

Tout comme nous exerçons une pression sur une surface en raison de la gravité, notre atmosphère en fait autant. Nous vivons au fond d’un océan de gaz qui devient progressivement moins dense à mesure que l’altitude augmente. Environ 99 % de la masse de l’atmosphère se trouve à moins de 30 km de la surface de la Terre (figure 2.3.2.). Chaque point de la surface de la Terre subit une pression nette appelée pression barométrique. La pression exercée par l’atmosphère est considérable : une colonne de 1 m², mesurée du niveau de la mer au sommet de l’atmosphère, a une masse d’environ 10 000 kg, ce qui donne une pression d’environ 101 kPa. Cependant, nous ne percevons généralement pas cette pression car nous y sommes physiologiquement adaptés !

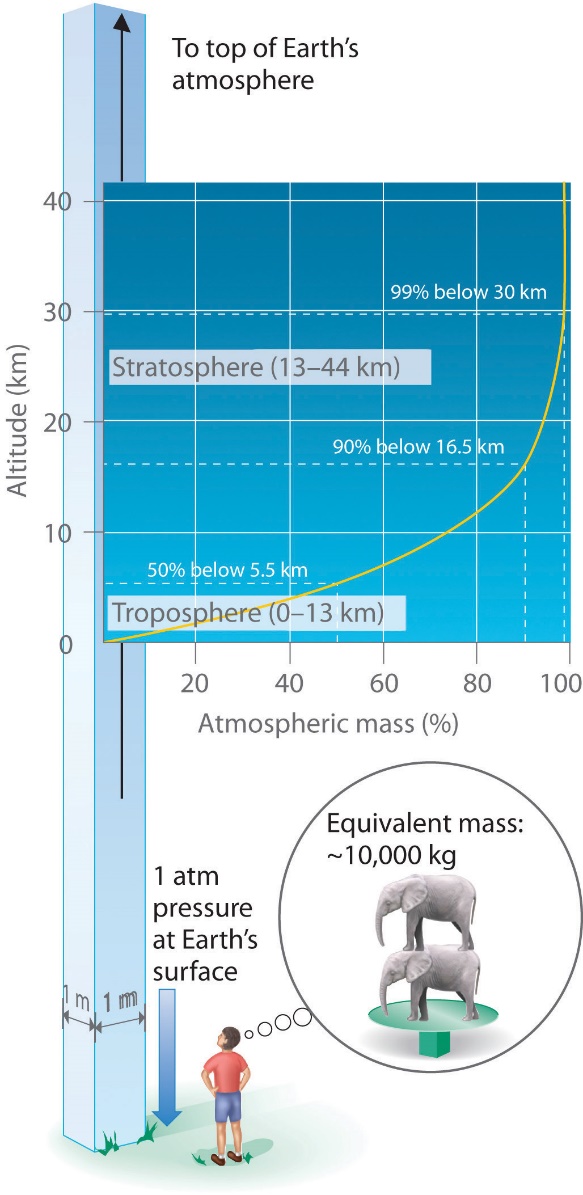
Figure 2.3.2. Pression barométrique. Chaque mètre carré de la surface de la Terre supporte une colonne d’air de plus de 200 km de haut et pesant environ 10 000 kg à la surface de la Terre.

La pression barométrique peut être mesurée à l’aide d’un baromètre, un appareil inventé en 1643 par un des étudiants de Galilée, Evangelista Torricelli (1608-1647). Comme le montre la figure 2.3.3, un baromètre peut être construit à partir d’un long tube de verre fermé à une extrémité. Il est rempli de mercure et placé à l’envers dans un plat de mercure sans laisser entrer d’air dans le tube. Une partie du mercure s’écoulera du tube, mais une colonne relativement haute restera à l’intérieur. Pourquoi tout le mercure ne s’écoule-t-il pas ? La gravité exerce certainement une force descendante sur le mercure dans le tube, mais elle est contrariée par la pression de l’atmosphère qui pousse vers le bas la surface du mercure dans le plat, ce qui a pour effet net de pousser le mercure vers le haut dans le tube. Comme il n’y a pas d’air au-dessus du mercure à l’intérieur du tube dans un baromètre correctement rempli (il contient un vide), il n’y a pas de pression qui pousse la colonne vers le bas. Ainsi, le mercure sort du tube jusqu’à ce que la pression exercée par la colonne de mercure elle-même équilibre exactement la pression de l’atmosphère. La pression exercée par la colonne de mercure peut être exprimée comme suit

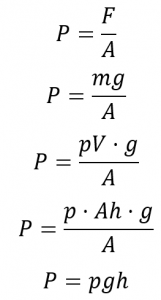
avec

g est l’accélération gravitationnelle,

m est la masse,

ρ est la densité,

V est le volume,

A est la zone inférieure, et

h est la hauteur de la colonne de mercure.

Dans des conditions météorologiques normales au niveau de la mer, les deux forces s’équilibrent lorsque le sommet de la colonne de mercure se trouve à environ 760 mm au-dessus du niveau du mercure dans la parabole, comme le montre la figure 2.3.3. Cette valeur varie en fonction des conditions météorologiques et de l’altitude. À Denver, dans le Colorado, par exemple, à une altitude d’environ 1 mile, ou 1609 m (5280 ft), la hauteur de la colonne de mercure est de 630 mm au lieu de 760 mm.

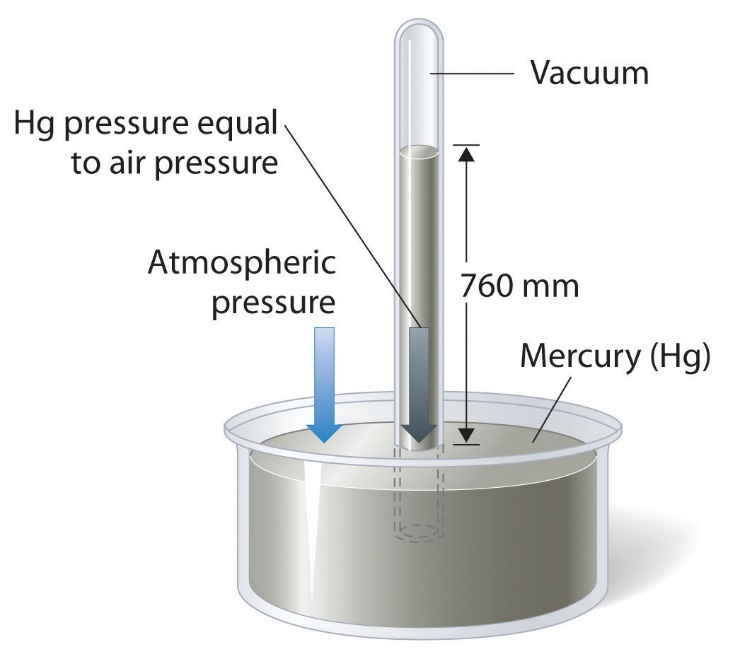
Figure 2.3.3. Un baromètre à mercure. La pression exercée par l’atmosphère à la surface du bassin de mercure soutient une colonne de mercure dans le tube d’environ 760 mm de hauteur. Comme le point d’ébullition du mercure est assez élevé (356,73 °C), la vapeur de mercure est négligeable dans l’espace au-dessus de la colonne de mercure.

Les baromètres à mercure sont utilisés depuis si longtemps pour mesurer la pression barométrique qu’ils ont leur propre unité de pression : le millimètre de mercure (mmHg), souvent appelé Torr, d’après Torricelli. La pression barométrique standard est la pression barométrique nécessaire pour supporter une colonne de mercure d’exactement 760 mm de hauteur ; cette pression est également appelée 1 atmosphère (atm). Ces unités sont également liées au pascal :

1 atm = 760 mmHg

      = 760 Torr

                  = 1.01325 × 10⁵ Pa

          = 101.325 kPa

         = 1.01325 bar

          = 14.6959 psi

Ainsi, une pression de 1 atm équivaut exactement à 760 mmHg.

Nous sommes tellement habitués à vivre sous cette pression que nous ne la remarquons jamais. Ce que nous remarquons, au contraire, ce sont les changements de pression, comme lorsque nos oreilles s’ouvrent dans les ascenseurs rapides des gratte-ciels ou dans les avions lors de changements rapides d’altitude. Nous utilisons la pression barométrique de nombreuses façons. Nous pouvons utiliser une paille à boire car le fait de la sucer enlève de l’air et réduit ainsi la pression à l’intérieur de la paille. La pression barométrique qui pousse le liquide dans le verre vers le bas force ensuite le liquide à monter dans la paille.

Pour en savoir plus sur le baromètre et son histoire, regardez la vidéo suivante.

Exemple 2.3.4 – Pression barométrique

Un professeur de chimie générale a visité le parc national des montagnes Rocheuses il y a plusieurs années. Après avoir quitté d’un aéroport situé au niveau de la mer dans l’est des États-Unis, il est arrivé à Denver (altitude 5280 ft), a loué une voiture et s’est rendu au sommet de l’autoroute à l’extérieur d’Estes Park (altitude 14 000 ft). Il a remarqué que même un léger effort était très difficile à cette altitude, où la pression barométrique n’est que de 454 mmHg. Convertissez cette pression en

1. atmosphères (atm).

2. bar.

Solution

1. A partir des facteurs de conversion, nous avons 1 atm = 760 mmHg = 101,325 kPa. La pression à 14 000 pieds en atm est donc

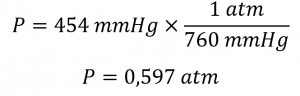
2. La pression en bar est donnée par

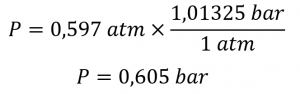
Vérifiez votre apprentissage 2.3.3 – Pression barométrique

Le mont Everest, à 29 028 pieds au-dessus du niveau de la mer, est la plus haute montagne du monde. La pression barométrique normale à cette altitude est d’environ 0,308 atm. Convertissez cette pression en

1. Millimètres de mercure

2. Bar

3. Pascals

Réponse

1. 234 mmHg

2. 0,312 bar

3. 31 200 Pa

Manomètres

Les baromètres mesurent la pression barométrique, mais les manomètres mesurent les pressions des échantillons de gaz contenus dans un appareil. La caractéristique principale d’un manomètre est un tube en forme de U contenant du mercure (ou parfois un autre liquide non volatil). Un manomètre fermé est représenté schématiquement à la figure 2.3.4(a). Lorsque l’ampoule ne contient pas de gaz (c’est-à-dire lorsque son intérieur est un quasi-vide), les hauteurs des deux colonnes de mercure de part et d’autre du tube en U sont identiques car l’espace au-dessus du mercure de gauche est également un quasi-vide (il ne contient que des traces de vapeur de mercure). Si un gaz est ajouté à l’ampoule de droite, il exercera une pression sur le mercure de la colonne de droite, et les deux colonnes de mercure ne seront plus de la même hauteur. La différence entre les hauteurs des deux colonnes est égale à la pression du gaz.

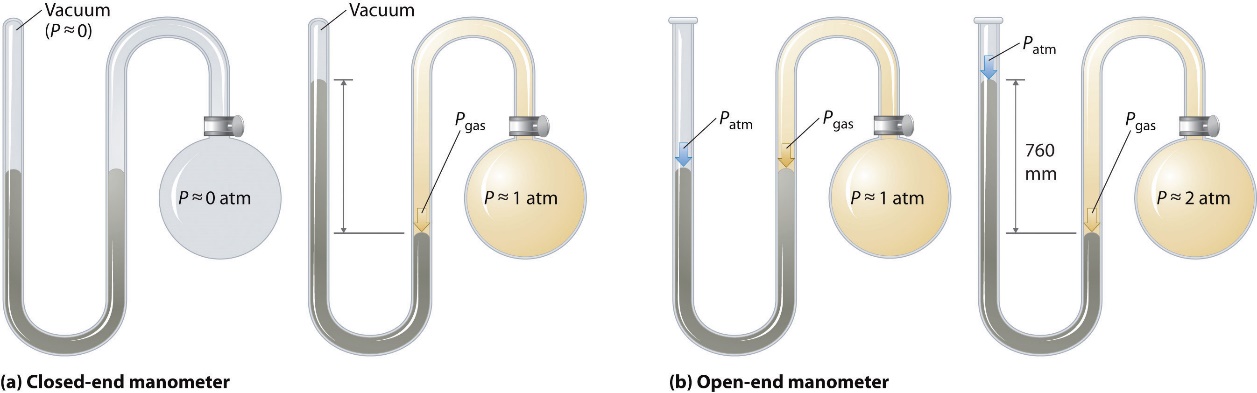
Figure 2.3.4. Les deux types de manomètre. (a) Dans un manomètre fermé, l’espace au-dessus de la colonne de mercure à gauche (le bras de référence) est essentiellement un vide (P ≈ 0), et la différence de hauteur des deux colonnes donne directement la pression du gaz contenu dans l’ampoule. (b) Dans un manomètre à extrémité ouverte, le bras gauche (de référence) est ouvert à l’atmosphère (P ≈ 1 atm), et la différence de hauteur des deux colonnes donne la différence entre la pression barométrique et la pression du gaz dans l’ampoule.

Si le tube est ouvert à l’atmosphère au lieu d’être fermé, comme dans le cas du manomètre à extrémité ouverte illustré à la figure 2.3.4(b). alors les deux colonnes de mercure ont la même hauteur uniquement si le gaz dans l’ampoule a une pression égale à la pression barométrique. Si le gaz dans l’ampoule a une pression plus élevée, le mercure dans le tube ouvert sera poussé vers le haut par le gaz qui pousse vers le bas le mercure dans l’autre bras du tube en forme de U. La pression du gaz dans l’ampoule est donc la somme de la pression barométrique (mesurée avec un baromètre) et de la différence de hauteur des deux colonnes. Si le gaz dans l’ampoule a une pression inférieure à celle de l’atmosphère, alors la hauteur du mercure sera plus grande dans le bras fixé à l’ampoule. Dans ce cas, la pression du gaz dans l’ampoule est la pression barométrique moins la différence entre les hauteurs des deux colonnes.

Pour en savoir plus sur les manomètres, regardez la vidéo suivante.

Exemple 2.3.5 – Appliquer des théories : baromètres et manomètres

Supposons que vous vouliez construire un manomètre fermé pour mesurer des pressions de gaz dans la gamme 0,000-0,200 atm. En raison de la toxicité du mercure, vous décidez d’utiliser de l’eau plutôt que du mercure. De quelle hauteur de colonne d’eau avez-vous besoin ? (La densité de l’eau est de 1,00 g/cm³ ; la densité du mercure est de 13,53 g/cm³).

Solution

En millimètres de mercure, une pression de gaz de 0,200 atm est

Pour utiliser un manomètre à mercure, il faudrait une colonne de mercure d’au moins 152 mm de haut.

L’eau étant moins dense que le mercure, il faut une colonne d’eau plus haute pour obtenir la même pression qu’une colonne de mercure donnée. La hauteur nécessaire pour une colonne remplie d’eau correspondant à une pression de 0,200 atm est proportionnelle au rapport entre la densité du mercure et la densité de l’eau

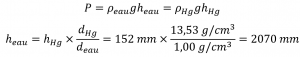
La réponse est logique : il faut une colonne plus haute d’un liquide moins dense pour obtenir la même pression.

Vérifiez votre apprentissage 2.3.4 – Appliquer des théories : baromètres et manomètres

Supposons que vous vouliez concevoir un baromètre pour mesurer la pression barométrique dans un environnement qui est toujours plus chaud que 30 °C. Pour éviter d’utiliser du mercure, vous décidez d’utiliser du gallium, qui fond à 29,76 °C ; la densité du gallium liquide à 25 °C est de 6,114 g/cm³. De quelle hauteur de colonne de gallium avez-vous besoin si P = 1,00 atm ?

Réponse

1.68 m

Vérifiez votre apprentissage 2.3.5 – Appliquer des théories : baromètres et manomètres

Considérez le manomètre ouvert suivant :

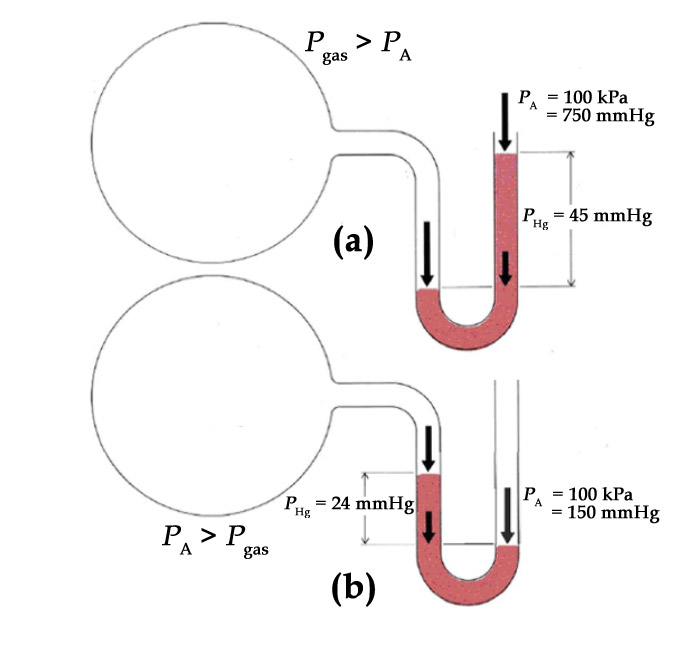
Que peut-on conclure sur la pression du gaz dans l’ampoule a) ? Ampoule b) ?

Réponse

La pression du gaz de l’ampoule a) est supérieure à celle de l’atmosphère. La pression du gaz de l’ampoule b) est inférieure à celle de l’atmosphère.

La formule dérivée de l’exemple 2.3.5 peut également nous aider dans d’autres domaines, comme l’hydrogéologie. Prenons par exemple le problème de la construction d’un puits pour obtenir de l’eau d’un aquifère souterrain. Nous pouvons appliquer une méthode similaire pour déterminer la profondeur maximale d’un puits si une simple pompe d’aspiration est utilisée pour extraire l’eau. Une pression barométrique externe de 1,00 atm correspondrait donc à une hauteur maximale de la colonne d’eau de :

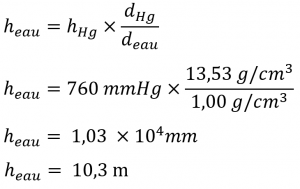
Une pompe d’aspiration n’est qu’une version plus sophistiquée d’une paille : elle crée un vide au-dessus d’un liquide et s’appuie sur la pression barométrique pour faire monter le liquide dans un tube. Si une pression barométrique de 1,00 atm correspond à une colonne d’eau de 10,3 m, il est physiquement impossible que la pression barométrique fasse monter l’eau dans un puits plus haut que celui-ci. Jusqu’à l’invention des pompes électriques pour pousser mécaniquement l’eau à de plus grandes profondeurs, ce facteur limitait grandement les endroits où les gens pouvaient vivre, car il était difficile d’obtenir de l’eau de puits plus profonds que 33 pieds environ.

Volume

Le volume est défini comme la longueur multipliée par la largeur multipliée par la hauteur. Il est donc exprimé en mètres × mètres × mètres ou en mètres³ (m³), parfois appelés “mètres cubes”. Le mètre cube est une unité assez grande, mais on définit une autre unité un peu plus facile à gérer : le litre (L). Un litre correspond à 1/1000^ème (1 x 10^-3 m³) d’un mètre cube et représente un peu plus d’un quart de volume (figure 2.3.5.). Des préfixes peuvent également être utilisés avec l’unité litre, on peut donc parler de millilitres (1 mL = 1 x 10^-3 L = 1 x 10^-6 m³), de microlitres (1 µL = 1 x 10^-6 L = 1 x 10^-9 m³⁾, etc.

Une autre définition d’un litre est un dixième de mètre cube. Comme un dixième de mètre est de 10 cm, un litre est donc égal à 1000 cm³ (figure 2.3.5.). Comme 1 L est égal à 1000 ml, nous concluons que 1 ml est égal à 1 cm³ ; ces unités sont donc interchangeables.

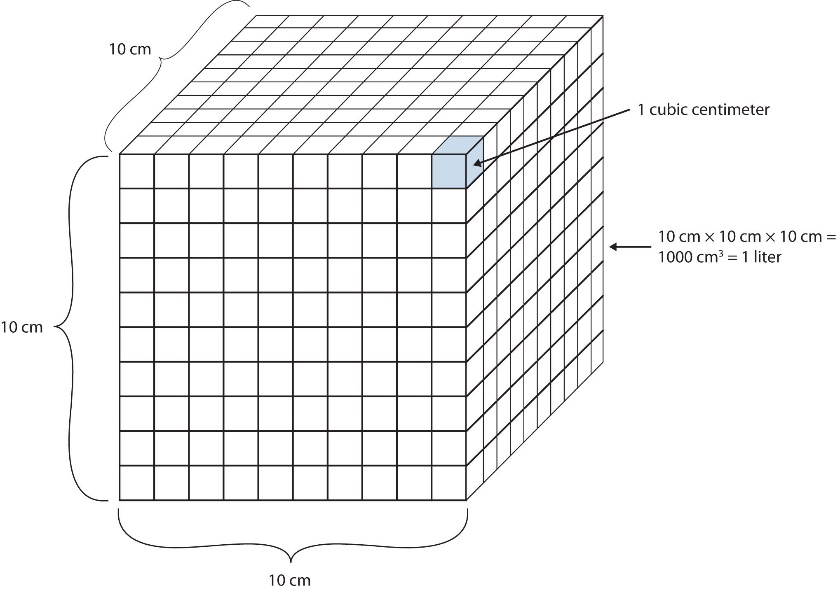
Figure 2.3.5. La taille d’un litre. Un litre équivaut à 1 000 cm³, donc 1 cm³ équivaut à 1 ml.

Température

L’une des quantités fondamentales en science est la température, qui est une mesure de la quantité moyenne d’énergie de mouvement, ou énergie cinétique, que contient un système. Les températures sont exprimées à l’aide d’échelles qui utilisent des unités appelées degrés. Il existe trois échelles utilisées pour rendre compte des températures. La figure 2.3.6. compare les trois échelles de température.

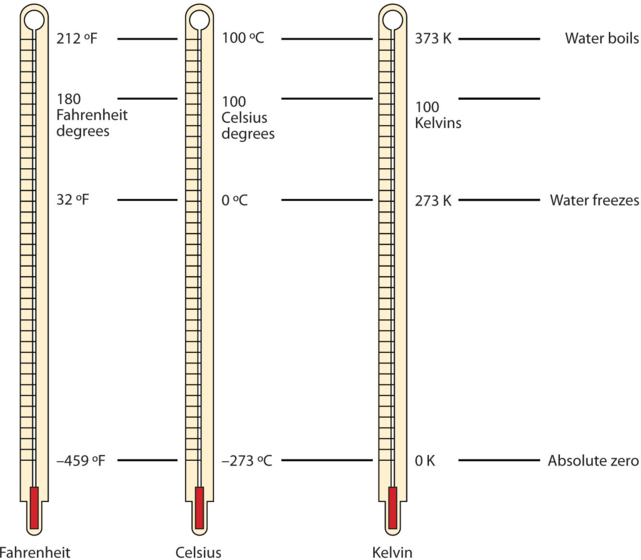
Figure 2.3.6. Températures en Fahrenheit, Celsius et Kelvin. Une comparaison des trois échelles de température. Ces thermomètres ont un liquide de couleur rouge qui contient de l’alcool et du colorant alimentaire. Les thermomètres d’aspect argenté contiennent du mercure, qui est une neurotoxine.

Les scientifiques utilisent d’autres échelles pour exprimer la température. Par exemple, l’échelle Celsius (symbolisée par °C et appelée “degrés Celsius”) définit 0 °C comme le point de congélation de l’eau et 100 °C comme le point d’ébullition de l’eau. Cette échelle est divisée en 100 divisions entre ces deux points de repère et s’étend aussi bien vers le haut que vers le bas. En comparant les échelles Fahrenheit et Celsius, on peut déterminer une conversion entre les deux échelles :

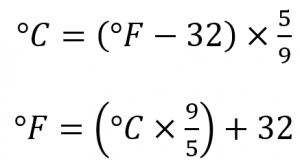
Notez que la science utilise presque exclusivement les échelles Celsius et Kelvin ; pratiquement aucun chimiste praticien n’exprime les températures mesurées en laboratoire avec l’échelle Fahrenheit, mais celle-ci est incluse ici dans un souci d’exhaustivité.

L’unité fondamentale de la température dans le SI est le Kelvin (K). L’échelle de température Kelvin (notez que le nom de l’échelle est en majuscules, mais l’unité elle-même est en minuscules) utilise des degrés de la même taille que le degré Celsius, mais l’échelle numérique est décalée de 273,15 unités vers le haut. C’est-à-dire que la conversion entre les échelles Kelvin et Celsius est la suivante :

K = ^∘C + 273,15

Dans la plupart des cas, il est acceptable d’utiliser 273 au lieu de 273,15 lors de la conversion en Kelvin.

La raison pour laquelle l’échelle Kelvin est définie de cette façon est qu’il existe une température minimale possible appelée zéro absolu (zéro kelvin). L’échelle de température Kelvizéro absolun est définie de telle sorte que 0 K est le zéro absolu, et la température est comptée vers le haut à partir de là. La température ambiante normale est d’environ 295 K, comme on le voit dans l’exemple suivant.

Exemple 2.3.6 – Température ambiante

Si la température ambiante normale est de 72,0 °F, quelle est la température ambiante en degrés Celsius et Kelvin ?

Solution

D’abord, nous déterminons la température en degrés Celsius :

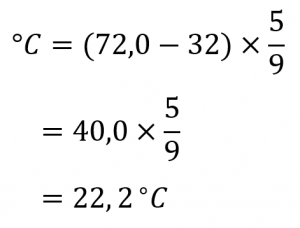
Ensuite, nous déterminons la température dans l’échelle Kelvin :

K = 22,2^∘C + 273,15

K = 295,4 K

Ainsi, la température ambiante est d’environ 295 K.

Questions

★ Questions

1. Avant une plongée, une bouteille de plongée est remplie d’air jusqu’à ce que le manomètre indique 200,0 bars. Convertissez cette pression en :

a. atm

b. Pa et kPa

c. mmHg

2. Un ballon à fond rond d’un diamètre de 17,0 cm contient 1,00 mole d’hydrogène gazeux à une pression de 333 Torr. Quelle est la force, en Newtons, exercée sur les parois intérieures du ballon ?

3. Un contenant cubique mesurant 40,0 cm x 40,0 cm x 40,0 cm pèse 255,0 g lorsqu’il est évacué (vide). Lorsqu’il est rempli de xénon, la pression générée par le poids du récipient sur sa face inférieure est de 21,65 kPa. Quelle quantité de xénon, en moles, se trouve dans le contenant?

4. La pression barométrique est directement liée aux conditions météorologiques : une pression barométrique stable et élevée indique le beau temps, tandis qu’une pression en baisse avertit de l’approche d’un système dépressionnaire, apportant le mauvais temps. Au cours d’un après-midi, la pression barométrique au-dessus d’Ottawa passe de 102,27 kPa à 99,85 kPa. Quel est le changement de la quantité de force appliquée (en Newtons) sur la surface d’une table de pique-nique de 1,5 m x 2,5 m, lorsque la pression atmosphérique diminue ?

5. Sur le site de la Croix-Rouge canadienne, vous trouverez les conseils suivants sur ce qu’il faut faire si vous tombez à travers la glace sur une étendue d’eau gelée :

“Tendre la main vers l’avant sur la glace brisée sans pousser vers le bas. Donner des coups de pied dans les jambes pour essayer de mettre le corps en position horizontale. Continuez à donner des coups de pied aux jambes et rampez sur la glace. Lorsque vous êtes de retour sur la glace, rampez sur le ventre ou éloignez-vous de la zone ouverte avec vos bras et vos jambes aussi loin que possible. Ne vous mettez pas debout ! Cherchez le rivage et assurez-vous que vous rampez dans la bonne direction”.

Pourquoi est-il important de ramper ou de se rouler en dehors de l’espace ouvert, au lieu de se lever et de s’éloigner rapidement ?

6. Les baromètres et manomètres sont toujours fabriqués à l’aide de liquides non volatils pour mesurer la pression. Donnez une raison pour laquelle les liquides volatils seraient inappropriés.

7. La pression d’un échantillon de gaz est mesurée au niveau de la mer avec un manomètre à bout fermé. Le liquide contenu dans le manomètre est du mercure. Déterminez la pression du gaz entrant :

a. Torr

b. Pa

c. bar

8. La pression d’un échantillon de gaz est mesurée à l’aide d’un manomètre à extrémité ouverte, partiellement illustré à droite. Le liquide contenu dans le manomètre est du mercure. En supposant que la pression atmosphérique est de 1,010 atm, on détermine la pression du gaz dans le manomètre :

a. Torr

b. Pa

c. bar

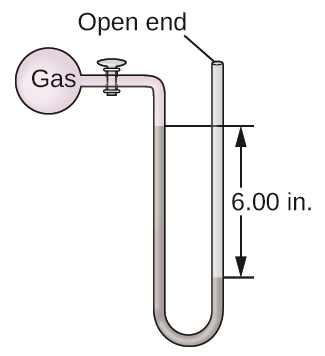
Lorsque vous prenez l’ascenseur jusqu’au dernier étage d’un gratte-ciel, vous pouvez remarquer la sensation de vos oreilles qui “claquent”. Quel changement physiologique ressentez-vous ?

Réponses

1.

a. 197,4 atm

b. 2,000 x 10⁴ kPa

c. 1,50 x 10⁵ mmHg

4. 9 075 N

5. En répartissant votre poids sur une plus grande surface, vous diminuez la pression appliquée sur la glace, ce qui réduit le risque de tomber à nouveau à travers la glace.

6. Si un liquide volatil était utilisé, il produirait une vapeur qui exercerait sa propre pression partielle contre la surface du liquide, ce qui entraînerait des mesures erronées.

7.

a. 264 Torr

b. 35,200 Pa

c. 0,352 bar

8.

a. P_gas = 615,2 Torr

b. P(en Pa) = 8,20 x 10⁴ Pa

c. P(en bar) = 0,820 bar

9. Au fur et à mesure que vous montez en altitude, la pression atmosphérique à l’extérieur de votre corps diminue. L’air emprisonné à l’intérieur de votre corps dans vos tubes d’Eustache se dilate, augmentant la pression dans votre oreille moyenne, jusqu’à ce que les tubes s’ouvrent soudainement. Lorsqu’ils s’ouvrent, la pression est égalisée et vos tympans bougent, créant la sensation de “pop”.