1.4 – Stœchiométrie des solutions

Molarité

Dans les sections précédentes, nous nous sommes concentrés sur la composition des substances : des échantillons de matière qui ne contiennent qu’un seul type d’élément ou de composé. Cependant, les mélanges – des échantillons de matière contenant deux ou plusieurs substances physiquement combinées – sont plus fréquents dans la nature que les substances pures. Tout comme pour une substance pure, la composition relative d’un mélange joue un rôle important dans la détermination de ses propriétés. La quantité relative d’oxygène dans l’atmosphère d’une planète détermine sa capacité à maintenir une vie aérobie. Les quantités relatives de fer, de carbone, de nickel et d’autres éléments dans l’acier (un mélange solide appelé “alliage”) déterminent sa force physique et sa résistance à la corrosion. La quantité relative de l’ingrédient actif d’un médicament détermine son efficacité à obtenir l’effet pharmacologique souhaité. La quantité relative de sucre dans une boisson détermine sa douceur (voir figure 1.4.1.). Dans cette section, nous allons décrire l’une des façons les plus courantes de quantifier les compositions relatives des mélanges.

Figure 1.4.1. Le sucre est l’un des nombreux composants du mélange complexe connu sous le nom de café. La quantité de sucre dans une quantité donnée de café est un facteur déterminant de la douceur de la boisson. (crédit : Jane Whitney)

Solutions

Nous avons précédemment défini les solutions comme des mélanges homogènes, ce qui signifie que la composition du mélange (et donc ses propriétés) est uniforme dans tout son volume. Les solutions sont fréquentes dans la nature et ont également été mises en œuvre dans de nombreuses formes de technologie artificielle. Nous examinerons plus en détail les propriétés des solutions dans le chapitre sur les solutions et les colloïdes, mais nous présenterons ici certaines des propriétés de base des solutions.

La quantité relative d’un composant donné de la solution est connue sous le nom de concentration. Souvent, mais pas toujours, une solution contient un composant dont la concentration est nettement supérieure à celle de tous les autres composant. Ce composant est appelée le solvant et peut être considéré comme le milieu dans lequel les autres composants sont dispersés, ou dissous. Les solutions dans lesquelles l’eau est le solvant sont, bien sûr, très courantes sur notre planète. Une solution dans laquelle l’eau est le solvant est appelée une solution aqueuse.

Un soluté est un composant d’une solution qui est généralement présente à une concentration beaucoup plus faible que le solvant. Les concentrations de solutés sont souvent décrites par des termes qualitatifs tels que dilué (de concentration relativement faible) et concentré (de concentration relativement élevée).

Les concentrations peuvent être évaluées quantitativement en utilisant une grande variété d’unités de mesure, chacune convenant à des applications particulières. La molarité (M) est une unité de concentration utile pour de nombreuses applications en chimie. La molarité est définie comme le nombre de moles de soluté dans exactement 1 litre (1 L) de la solution :

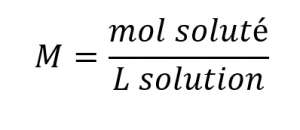
Exemple 1.4.1 – Calcul des concentrations molaires

Un échantillon de 355 ml de boisson rafraîchissante contient 0,133 mol de saccharose (sucre de table). Quelle est la concentration molaire de saccharose dans la boisson ?

Solution

Comme la quantité molaire du soluté et le volume de la solution sont tous deux donnés, la molarité peut être calculée en utilisant la définition de la molarité. Selon cette définition, le volume de la solution doit être converti de mL en L :

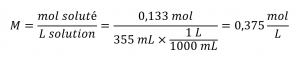
Vérifiez votre apprentissage 1.4.1 – Calcul des concentrations molaires

Une cuillère à théde sucre de table contient environ 0,01 mol de saccharose. Quelle est la molarité du saccharose si une cuillère à thé de sucre a été dissoute dans une tasse de thé d’un volume de 200 ml ?

  Réponse

0,05 mol/L

Exemple 1.4.2 – Dérivation des moles et des volumes à partir des concentrations molaires

Quelle est la quantité de sucre (mol) contenue dans une petite gorgée (~10 ml) de la boisson non alcoolisée de l’exemple précédent ?

Solution

Dans ce cas, on peut réarranger la définition de la molarité pour isoler la quantité recherchée, les moles de sucre. Nous substituons alors la valeur de la molarité que nous avons dérivée dans l’exemple précédent, 0,375 mol/L :

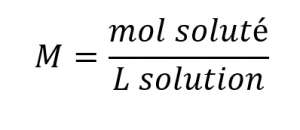
Vérifiez votre apprentissage 1.4.2 – Dérivation des moles et des volumes à partir des concentrations molaires

Quel volume (ml) du thé sucré décrit dans l’exemple précédent contient la même quantité de sucre (mol) que 10 ml de la boisson non alcoolisée de cet exemple ?

Réponse

80 ml

Exemple 1.4.3 – Calcul des concentrations molaires à partir de la masse du soluté

Le vinaigre blanc distillé (figure 1.4.2.) est une solution d’acide acétique, CH₃CO₂H, dans l’eau. Une solution de vinaigre de 0,500 L contient 25,2 g d’acide acétique. Quelle est la concentration de la solution d’acide acétique en unités de molarité ?

Figure 1.4.2. Le vinaigre blanc distillé est une solution d’acide acétique dans l’eau.

Solution

Comme dans les exemples précédents, la définition de la molarité est l’équation primaire utilisée pour calculer la quantité recherchée. Dans ce cas, la masse du soluté est fournie à la place de sa quantité molaire, nous devons donc utiliser la masse molaire du soluté pour obtenir la quantité de soluté en moles :

D’abord, trouvez le nombre de moles du soluté :

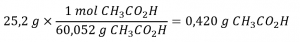
Ensuite, nous trouvons la molarité :

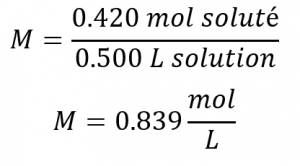
En d’autres termes:

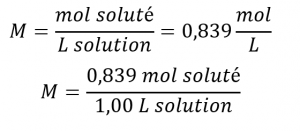
Vérifiez votre apprentissage 1.4.3 – Calcul des concentrations molaires à partir de la masse du soluté

Calculer la molarité de 6,52 g de CoCl₂ (128,9 g/mol) dissous dans une solution aqueuse d’un volume total de 75,0 ml.

Réponse

0,674 mol/L

Exemple 1.4.4 – Détermination de la masse de soluté dans un volume de solution donné

Combien de grammes de NaCl sont contenus dans 0,250 L d’une solution de 5,30 mol/L?

Solution

Le volume et la molarité de la solution sont spécifiés, de sorte que la quantité (mol) de soluté est facilement calculée comme le montre le deuxième exemple :

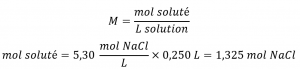
Enfin, cette quantité molaire est utilisée pour calculer la masse de NaCl :

Vérifiez votre apprentissage 1.4.4 – Détermination de la masse de soluté dans un volume de solution donné

Combien de grammes de CaCl₂ (110,98 g/mol) sont contenus dans 250,0 ml d’une solution de chlorure de calcium à 0,200 mol/L ?

Réponse

5,55 g de CaCl₂

Lorsque l’on effectue des calculs par étapes, comme dans l’exemple précédent, il est important de s’abstenir d’arrondir les résultats des calculs intermédiaires, ce qui peut entraîner des erreurs d’arrondi dans le résultat final. Dans l’exemple précédent, la quantité molaire de NaCl calculée dans la première étape, 1,325 mol, serait correctement arrondie à 1,32 mol si elle devait être déclarée ; cependant, bien que le dernier chiffre (5) ne soit pas significatif, il doit être retenu comme chiffre de garde dans le calcul intermédiaire. Si nous n’avions pas retenu ce chiffre de garde, le calcul final pour la masse de NaCl aurait été de 77,1 g, soit une différence de 0,3 g.

En plus de conserver un chiffre de garde pour les calculs intermédiaires, nous pouvons également éviter les erreurs d’arrondi en effectuant les calculs en une seule étape (voir l’exemple suivant). Cela permet d’éliminer les étapes intermédiaires, de sorte que seul le résultat final est arrondi.

Exemple 1.4.5 – Détermination du volume de solution contenant une masse donnée de soluté

Dans le troisième exemple, nous avons constaté que la concentration typique du vinaigre était de 0,839 mol/L. Quel volume de vinaigre contient 75,6 g d’acide acétique ?

Solution

Tout d’abord, utilisez la masse molaire pour calculer les moles d’acide acétique à partir de la masse donnée :

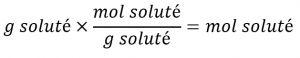
Ensuite, utilisez la molarité de la solution pour calculer le volume de la solution contenant cette quantité molaire de soluté :

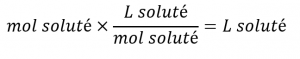
En combinant ces deux étapes en un seul rendement :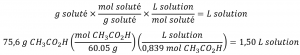

Vérifiez votre apprentissage 1.4.5 – Détermination du volume de solution contenant une masse donnée de soluté

Quel volume d’une solution de 1,50 mol/L de KBr contient 66,0 g de KBr ?

Réponse

0,370 L

Autres unités de concentration des solutions

Pourcentage de masse

Plus tôt dans ce chapitre, nous avons présenté la composition en pourcentage comme une mesure de la quantité relative d’un élément donné dans un composé. Les pourcentages sont également couramment utilisés pour exprimer la composition des mélanges, y compris les solutions. Le pourcentage de masse d’un composant de solution est défini comme le rapport entre la masse du composant et la masse de la solution, exprimé en pourcentage :

Nous sommes généralement plus intéressés par les pourcentages de masse des solutés, mais il est également possible de calculer le pourcentage de masse du solvant. Pour exprimer le pourcentage en masse, vous pouvez utiliser le système de mesure de votre choix, mais les mêmes unités doivent être utilisées en haut et en bas de l’équation et le dénominateur est toujours 100 (par exemple : g/100 g, oz/100 oz).

Le pourcentage de masse est également désigné par des noms similaires tels que pourcentage de masse, pourcentage de poids, poids/poids en pourcentage et autres variations sur ce thème. Le symbole le plus courant pour le pourcentage de masse est simplement le signe du pourcentage, %, bien que des symboles plus détaillés soient souvent utilisés, notamment % de masse, % de poids et (w/w) %. L’utilisation de ces symboles plus détaillés peut éviter la confusion des pourcentages de masse avec d’autres types de pourcentages, tels que les pourcentages de volume (qui seront abordés plus loin dans cette section).

Les pourcentages de masse sont des unités de concentration populaires pour les produits de consommation. L’étiquette d’une bouteille typique d’eau de Javel liquide (figure 1.4.3.) indique que la concentration de son ingrédient actif, l’hypochlorite de sodium (NaOCl), est de 7,4 %. Par conséquent, un échantillon de 100,0 g d’eau de Javel contiendrait 7,4 g de NaOCl.

Figure 1.4.3. L’eau de Javel est une solution aqueuse d’hypochlorite de sodium (NaOCl). Cette marque a une concentration de 7,4 % de NaOCl en masse.

Exemple 1.4.6 – Calcul du pourcentage en fonction de la masse

Un échantillon de 5,0 g de liquide céphalo-rachidien contient 3,75 mg (0,00375 g) de glucose. Quel est le pourcentage en masse de glucose dans le liquide céphalo-rachidien ?

Solution

L’échantillon de liquide céphalo-rachidien contient environ 4 mg de glucose dans 5000 mg de liquide, de sorte que la fraction massique du glucose devrait être un peu inférieure à une partie sur 1000, soit environ 0,1 %. Substitution des masses données dans l’équation définissant les rendements en pourcentage de masse :

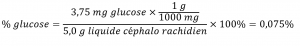
Ce résultat est tout à fait comparable à notre estimation approximative (un peu moins de la moitié de la concentration du stock, soit 5 mol/L).

Vérifiez votre apprentissage 1.4.6 – Calcul du pourcentage en fonction de la masse

Quelle est la concentration de la solution qui résulte de la dilution de 25,0 ml d’une solution de CH₃OH à 2,04 mol/L à 500,0 ml ?

Réponse

14,8 %

Exemple 1.4.7 – Calculs utilisant le pourcentage de masse

L’acide chlorhydrique “concentré” est une solution aqueuse de HCl à 37,2 % (en masse) qui est couramment utilisée comme réactif de laboratoire. La densité de cette solution est de 1,19 g/mL. Quelle est la masse de HCl contenue dans 0,500 L de cette solution ?

Solution

La concentration de HCl est proche de 40 %, de sorte qu’une portion de 100 g de cette solution contiendrait environ 40 g de HCl. Comme la densité de la solution n’est pas très différente de celle de l’eau (1 g/mL), une estimation raisonnable de la masse de HCl dans 500 g (0,5 L) de la solution est environ cinq fois supérieure à celle d’une portion de 100 g, soit 5 × 40 = 200 g. Afin de calculer la masse du soluté dans une solution à partir de son pourcentage de masse, nous devons connaître la masse correspondante de la solution. En utilisant la densité de la solution donnée, nous pouvons convertir le volume de la solution en masse, et ensuite utiliser le pourcentage de masse donné pour calculer la masse du soluté. Cette approche mathématique est décrite dans cet organigramme :

Pour une annulation correcte de l’unité, le volume de 0,500 L est converti en 500 mL, et le pourcentage de masse est exprimé sous forme de rapport, 37,2 g de HCl/100 g de solution :

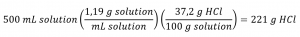
Cette masse de HCl correspond à notre estimation approximative de 200 g.

Vérifiez votre apprentissage 1.4.7 – Calculs utilisant le pourcentage de masse

Quel volume de solution concentrée de HCl contient 125 g de HCl ?

Réponse

282 ml

Volume Pourcentage

Les volumes de liquide sur une large gamme de magnitudes sont mesurés de manière pratique à l’aide d’équipements de laboratoire courants et relativement peu coûteux. La concentration d’une solution formée par la dissolution d’un soluté liquide dans un solvant liquide est donc souvent exprimée en pourcentage de volume, % vol ou (v/v)% :

Exemple 1.4.8 – Calculs utilisant le pourcentage de volume

L’alcool à friction (isopropanol) est généralement vendu sous forme de solution aqueuse à 70 % vol. Si la densité de l’alcool isopropylique est de 0,785 g/mL, combien de grammes d’alcool isopropylique sont présents dans une bouteille de 355 ml d’alcool à friction ?

Solution

Selon la définition du pourcentage de volume, le volume d’isopropanol est de 70 % du volume total de la solution. En multipliant le volume d’isopropanol par sa densité, on obtient la masse requise :

Vérifiez votre apprentissage 1.4.8 – Calculs utilisant le pourcentage de volume

Le vin contient environ 12 % d’éthanol (CH₃CH₂OH) en volume. L’éthanol a une masse molaire de 46,06 g/mol et une densité de 0,789 g/ml. Combien de moles d’éthanol sont présentes dans une bouteille de vin de 750 ml ?

Réponse

1,5 mol d’éthanol

Masse-Volume Pourcentage

Les unités de pourcentage “mixtes”, dérivées de la masse du soluté et du volume de la solution, sont populaires pour certaines applications biochimiques et médicales. Un pourcentage masse-volume est un rapport entre la masse d’un soluté et le volume de la solution, exprimé en pourcentage. Les unités spécifiques utilisées pour la masse du soluté et le volume de la solution peuvent varier en fonction de la solution. Par exemple, une solution saline physiologique, utilisée pour préparer des fluides intraveineux, a une concentration de 0,9 % masse/volume (m/v), ce qui indique que la composition est de 0,9 g de soluté pour 100 ml de solution. La concentration de glucose dans le sang (communément appelée “sucre sanguin”) est également généralement exprimée en termes de rapport masse/volume. Bien qu’elle ne soit pas explicitement exprimée en pourcentage, sa concentration est généralement donnée en milligrammes de glucose par décilitre (100 ml) de sang (figure 1.4.4.).

Figure 1.4.4. Les unités de masse-volume “mixtes” sont couramment rencontrées dans les établissements médicaux. (a) La concentration de NaCl du sérum physiologique est de 0,9 % (m/v). (b) Cet appareil mesure le taux de glucose dans un échantillon de sang. La plage normale de concentration de glucose dans le sang (à jeun) est d’environ 70-100 mg/dL. (crédit a : modification du travail par “The National Guard”/Flickr ; crédit b : modification du travail par Biswarup Ganguly)

Parties par million et parties par milliard

Les très faibles concentrations de solutés sont souvent exprimées à l’aide de petites unités appropriées telles que les parties par million (ppm) ou les parties par milliard (ppb). Il existe également des unités ppm et ppb définies par rapport au nombre d’atomes et de molécules.

Les définitions des ppm et des ppb, basées sur la masse, sont données ici :

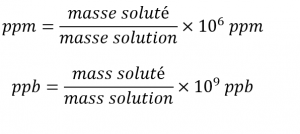
Les ppm et les ppb sont des unités pratiques pour rendre compte des concentrations de polluants et d’autres contaminants à l’état de traces dans l’eau. Les concentrations de ces contaminants sont généralement très faibles dans les eaux traitées et naturelles, et leurs niveaux ne peuvent dépasser des seuils de concentration relativement bas sans provoquer d’effets néfastes sur la santé et la faune. Par exemple, l’EPA a déterminé que le niveau maximal sans danger de l’ion fluorure dans l’eau du robinet est de 4 ppm. Les filtres à eau en ligne sont conçus pour réduire la concentration de fluorure et de plusieurs autres contaminants à l’état de traces dans l’eau du robinet (figure 1.4.5.).

Figure 1.4.5. (a) Dans certaines régions, les concentrations de contaminants à l’état de traces peuvent rendre l’eau du robinet non filtrée impropre à la consommation et à la cuisine. (b) Les filtres à eau en ligne réduisent la concentration de solutés dans l’eau du robinet. (crédit a : modification des travaux de Jenn Durfey ; crédit b : modification des travaux de “vastateparkstaff“/Wikimedia commons)

Exemple 1.4.9 – Calcul des concentrations en parties par million et en parties par milliard

Selon l’EPA, lorsque la concentration de plomb dans l’eau du robinet atteint 15 ppb, certaines mesures correctives doivent être prises. Quelle est cette concentration en ppm ? À cette concentration, quelle masse de plomb (μg) serait contenue dans un verre d’eau typique (300 ml) ?

Solution

Les définitions des unités ppm et ppb peuvent être utilisées pour convertir la concentration donnée de ppb en ppm. La comparaison de ces deux définitions d’unités montre que le ppm est 1000 fois supérieur au ppb (1 ppm = 10³ ppb). Ainsi:

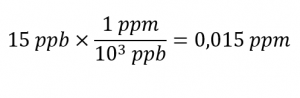
La définition de l’unité ppb peut être utilisée pour calculer la masse demandée si la masse de la solution est fournie. Cependant, seul le volume de la solution (300 ml) est donné, il faut donc utiliser la densité pour obtenir la masse correspondante. Nous pouvons supposer que la densité de l’eau du robinet est à peu près la même que celle de l’eau pure (~1,00 g/mL), puisque les concentrations des substances dissoutes ne doivent pas être très importantes. En réorganisant l’équation définissant l’unité ppb et en remplaçant les quantités données, on obtient

Enfin, il faut convertir cette masse dans l’unité de microgrammes demandée :

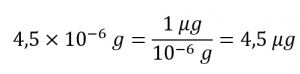
Vérifiez votre apprentissage 1.4.9 – Calcul des concentrations en parties par million et en parties par milliard

a. L’eau de votre robinet contient 4,0 ppm de fluorure. Un site web affirme que le fluorure est dangereux et que vous pouvez être empoisonné si vous en consommez plus de 5,0 grammes. Si vous buvez 6 verres (chaque verre équivaut à 0,40 L) d’eau du robinet par jour, combien de temps faudra-t-il avant que vous ne consommiez 5,0 grammes de fluorure (en supposant qu’il ne quitte JAMAIS votre corps ?).

b. On a déterminé qu’un échantillon de 50,0 g d’eaux usées industrielles contenait 0,48 mg de mercure. Exprimez la concentration de mercure dans les eaux usées en unités ppm et ppb.

Réponse

a. 520 jours

b. 9,6 ppm, 9600 ppb

Molalité

Une dernière façon d’exprimer la concentration d’une solution est par sa molalité. La molalité (b) d’une solution correspond aux moles de soluté divisées par les kilogrammes de solvant. Une solution qui contient 1,0 mole de NaCl dissous dans 1,0 kg d’eau est une solution “un-molale” de chlorure de sodium. Le symbole de la molalité est un b minuscule écrit en italique.

La molalité ne diffère de la molarité qu’au niveau du dénominateur. Alors que la molarité est basée sur les litres de solution, la molalité est basée sur les kilogrammes de solvant. Les concentrations exprimées en molalité sont utilisées pour étudier les propriétés des solutions liées à la pression de vapeur et aux changements de température. La molalité est utilisée parce que sa valeur ne change pas avec les changements de température. Le volume d’une solution, en revanche, dépend légèrement de la température.

  Exemple 1.4.10 – Molalité

Déterminez la molalité d’une solution préparée en dissolvant 28,60 g de glucose (C₆H₁₂O₆) dans 250 g d’eau.

Solution

Convertissez les grammes de glucose en moles et divisez-les par la masse de l’eau en kilogrammes :

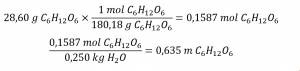
La réponse représente les moles de glucose par kilogramme d’eau et comporte trois chiffres significatifs.

La molarité et la valeur des solutions aqueuses diluées sont étroitement liées, car la densité de ces solutions est relativement proche de 1,0 g/ml. Cela signifie que 1,0 L de solution a une masse de près de 1,0 kg. Lorsque la solution devient plus concentrée, sa densité ne sera pas aussi proche de 1,0 g/mL et la valeur de la molarité sera différente de celle de la masse. Pour les solutions contenant des solvants autres que l’eau, la molalité sera très différente de la molarité. Assurez-vous que vous faites attention à la quantité utilisée dans un problème donné.

L’eau comme solvant universel

L’eau est surnommée un solvant universel car elle dissout de nombreuses substances en raison des fortes interactions entre les molécules d’eau et celles d’autres substances. L’entropie est une autre force motrice permettant à un liquide de se dissoudre ou de se mélanger à d’autres substances (sachez juste pour l’instant que l’entropie décrit la dispersion de la matière et/ou de l’énergie au sein d’un système ou la mesure du désordre d’un système). Le mélange augmente le désordre ou l’entropie. Vous en apprendrez plus sur l’entropie dans le document CHM2531/CHM2532.

Effet hydrophobe et effet hydrophile

En raison de son moment dipolaire élevé et de sa capacité à donner et à accepter des protons pour la liaison hydrogène, l’eau est un excellent solvant pour les substances polaires et les électrolytes, qui sont constitués d’ions. Les molécules qui interagissent fortement avec ou aiment les molécules d’eau sont hydrophiles, en raison de la liaison hydrogène, des attractions polaires-ioniques ou polaires-polaires. Les molécules non polaires qui ne se mélangent pas à l’eau sont hydrophobes ou lipophiles car elles ont tendance à se dissoudre dans l’huile. Les grosses molécules telles que les protéines et les acides gras qui ont des parties hydrophiles et hydrophobes sont amphipathiques ou amphiphiles. Les molécules d’eau se mêlent fortement aux parties hydrophiles par le biais d’une interaction dipôle-dipôle ou d’une liaison hydrogène. Ce point sera examiné en détail dans le document CHM1721.

Dilution des solutions

La dilution est le processus par lequel la concentration d’une solution est diminuée par l’ajout de solvant. Par exemple, on pourrait dire qu’un verre de thé glacé se dilue de plus en plus à mesure que la glace fond. L’eau provenant de la fonte de la glace augmente le volume du solvant (eau) et le volume global de la solution (thé glacé), réduisant ainsi les concentrations relatives des solutés qui donnent son goût à la boisson (figure 1.4.6.).

Figure 1.4.6. Les deux solutions contiennent la même masse de nitrate de cuivre. La solution de droite est plus diluée car le nitrate de cuivre est dissous dans plus de solvant. (crédit : Mark Ott)

La dilution est également un moyen courant de préparer des solutions d’une concentration souhaitée. En ajoutant du solvant à une portion mesurée d’une solution mère plus concentrée, on peut obtenir une concentration particulière. Par exemple, les pesticides commerciaux sont généralement vendus sous forme de solutions dans lesquelles les ingrédients actifs sont beaucoup plus concentrés que ce qui est approprié pour leur application. Avant de pouvoir être utilisés sur les cultures, ces pesticides doivent être dilués. C’est également une pratique très courante pour la préparation d’un certain nombre de réactifs de laboratoire courants (figure 1.4.7.).

Figure 1.4.7. Une solution de KMnO₄ est préparée en mélangeant de l’eau avec 4,74 g de KMnO₄ dans un ballon. (crédit : modification du travail par Mark Ott)

Une simple relation mathématique peut être utilisée pour relier les volumes et les concentrations d’une solution avant et après le processus de dilution. Selon la définition de la molarité, la quantité molaire de soluté dans une solution (n) est égale au produit de la molarité de la solution (M) et de son volume en litres (L) :

n = ML

Des expressions comme celles-ci peuvent être écrites pour une solution avant et après sa dilution :

n₁ = M₁L₁

n₂ = M₂L₂

où les indices “1” et “2” se réfèrent respectivement à la solution avant et après la dilution. Comme le processus de dilution ne modifie pas la quantité de soluté dans la solution, n₁ = n₂. Ainsi, ces deux équations peuvent être égales l’une à l’autre :

M₁L₁ = M₂L₂

Cette relation est communément appelée l’équation de dilution. Bien que nous ayons dérivé cette équation en utilisant la molarité comme unité de concentration et le litre comme unité de volume, d’autres unités de concentration et de volume peuvent être utilisées, à condition que les unités s’annulent correctement selon la méthode du facteur-étiquette. Reflétant cette polyvalence, l’équation de dilution est souvent écrite sous une forme plus générale :

C₁V₁ = C₂V₂

où C et V sont respectivement la concentration et le volume.

Exemple 1.4.11 – Détermination de la concentration d’une solution diluée

Si 0,850 L d’une solution de 5,00 mol/L de nitrate de cuivre, Cu(NO₃)₂, est dilué à un volume de 1,80 L par l’ajout d’eau, quelle est la molarité de la solution diluée ?

Solution

On nous donne le volume et la concentration d’une solution mère, V₁ et C_1, et le volume de la solution diluée résultante, V₂. Nous devons trouver la concentration de la solution diluée, C₂. Nous réorganisons donc l’équation de dilution afin d’isoler C₂ :

C₁V₁ = C₂V₂

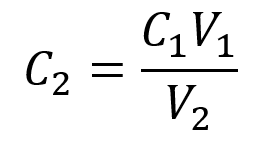
Comme la solution mère est diluée plus de deux fois (le volume passe de 0,85 L à 1,80 L), on s’attendrait à ce que la concentration de la solution diluée soit inférieure à la moitié de 5 mol/L. Nous comparerons cette estimation approximative au résultat calculé afin de vérifier l’absence d’erreurs grossières dans le calcul (par exemple, une substitution incorrecte des quantités données). En substituant les valeurs données aux termes du côté droit de cette équation, on obtient

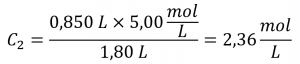
Ce résultat est tout à fait comparable à notre estimation approximative (un peu moins de la moitié de la concentration du stock, soit 5 mol/L).

Vérifiez votre apprentissage 1.4.11 – Détermination de la concentration d’une solution diluée

Quelle est la concentration de la solution qui résulte de la dilution de 25,0 ml d’une solution de CH3OH à 2,04 mol/L à 500,0 ml ?

Réponse

0,102 mol/L CH₃OH

Exemple 1.4.12 – Volume d’une solution diluée

Quel volume de 0,12 mol/L de HBr peut être préparé à partir de 11 ml (0,011 L) de 0,45 mol/L de HBr ?

Solution

On nous donne le volume et la concentration d’une solution mère, V₁ et C_1, et la concentration de la solution diluée résultante, C₂. Nous devons trouver le volume de la solution diluée, V₂. Nous réorganisons donc l’équation de dilution afin d’isoler V₂ :

C₁V₁ = C₂V₂

Comme la concentration diluée (0,12 mol/L) est légèrement supérieure au quart de la concentration initiale (0,45 mol/L), on s’attendrait à ce que le volume de la solution diluée soit environ quatre fois supérieur au volume initial, soit environ 44 ml. En substituant les valeurs données et en résolvant les volumes inconnus, on obtient ces résultats :

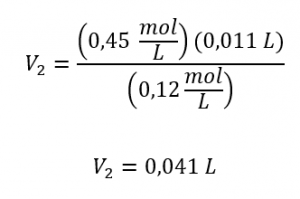
Le volume de la solution à 0,12 mol/L est de 0,041 L (41 ml). Le résultat est raisonnable et se compare bien avec notre estimation approximative.

Vérifiez votre apprentissage 1.4.10 – Volume d’une solution diluée

Une expérience de laboratoire demande 0,125 mol/L de HNO₃. Quel volume de 0,125 mol/L de HNO₃ peut être préparé à partir de 0,250 L de 1,88 mol/L de HNO₃ ?

Réponse

3,76 L

Exemple 1.4.13 – Volume d’une solution concentrée nécessaire à la dilution

Quel volume de 1,59 mol/L de KOH est nécessaire pour préparer 5,00 L de 0,100 mol/L de KOH ?

Solution

On nous donne la concentration d’une solution mère, C1, et le volume et la concentration de la solution diluée résultante, V₂ et C₂. Nous devons trouver le volume de la solution mère, V₁. Nous réorganisons donc l’équation de dilution afin d’isoler V₁ :

C₁V₁ = C₂V₂

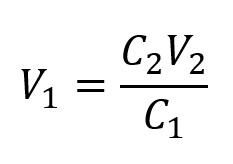
Comme la concentration de la solution diluée 0,100 mol/L est environ un seizième de celle de la solution mère (1,59 mol/L), on s’attendrait à ce que le volume de la solution mère soit environ un seizième de celui de la solution diluée, soit environ 0,3 litre. En substituant les valeurs données et en résolvant les volumes inconnus, on obtient des rendements :

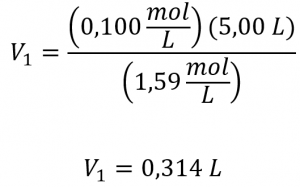
Ainsi, il faudrait 0,314 L de la solution à 1,59 mol/L pour préparer la solution souhaitée. Ce résultat est conforme à notre estimation approximative.

Vérifiez votre apprentissage 1.4.11 – Volume d’une solution concentrée nécessaire à la dilution

Quel volume d’une solution de glucose de 0,575 mol/L, C₆H₁₂O₆, peut-on préparer à partir de 50,00 ml d’une solution de glucose de 3,00 mol/L ?

Réponse

0,261 L

Équations moléculaires, ioniques complètes et ioniques nettes

Jusqu’à présent, nous n’avons examiné que les équations moléculaires. Il s’agit des équations de réaction équilibrée dans lesquelles nous avons pris en compte tous les atomes impliqués dans la réaction. Pour certaines réactions, ce n’est pas toute l’histoire. Dans les cas où nous avons des composés ioniques dissous dans l’eau, nous devons aller un peu plus loin.

Considérons la réaction de précipitation pour la formation du sulfate de baryum. La précipitation est un processus dans lequel une solution homogène réagit pour former un produit solide (appelé le précipité). L’équation chimique complète de cette réaction peut être écrite pour décrire ce qui se passe, et une telle équation est utile pour faire des calculs chimiques.

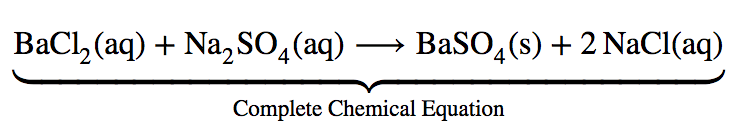
Équation chimique complète

Cependant, l’équation chimique complète ne représente pas vraiment les particules microscopiques (c’est-à-dire les ions) présentes dans la solution. Nous pourrions donc écrire ci-dessous l’équation ionique complète, où les sels aqueux sont écrits comme leurs ions individuels.

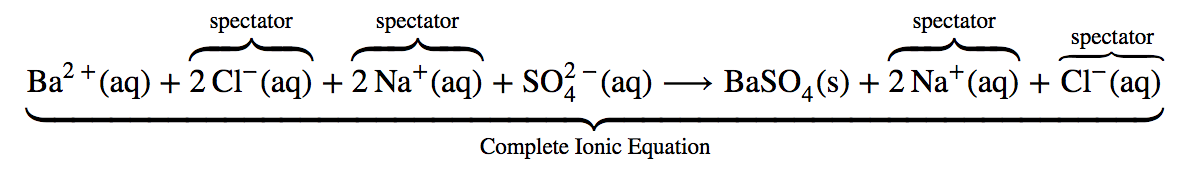
Équation ionique complète

L’équation ionique complète est assez complexe et comprend tellement d’ions différents qu’elle peut prêter à confusion. En tout cas, nous nous intéressons souvent au comportement indépendant des ions, et non au composé spécifique dont ils proviennent. Un précipité de BaSO₄ (s) se formera lorsque toute solution contenant du Ba²⁺ (aq) sera mélangée avec toute solution contenant du SO₂^-4 (aq) (à condition que les concentrations ne soient pas extrêmement faibles). Cela se produit indépendamment des ions Cl^–(aq) et Na⁺ (aq) dans l’équation ionique complète. Ces ions sont appelés ions spectateurs parce qu’ils ne participent pas à la réaction. Lorsque nous voulons mettre l’accent sur le comportement indépendant des ions, une équation ionique nette est écrite, en omettant les ions spectateurs. Pour la précipitation de BaSO4_, l’équation ionique nette est

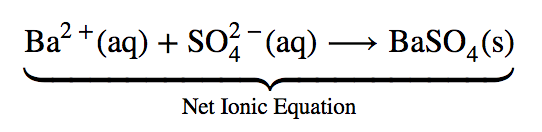
Équation ionique nette 

Exemple 1.4.14 – Précipitations d’AgCl

Lorsqu’une solution d’AgNO₃ est ajoutée à une solution de CaCl₂, l’AgCl insoluble précipite. Écrivez trois équations (équation chimique complète, équation ionique complète et équation ionique nette) qui décrivent ce processus.

Solution

Équation chimique complète :

2 AgNO₃ (aq) + CaCl₂ (aq)  →  2 AgCl (s) + Ca(NO₃)₂ (aq)

Les états et formules propres à tous les produits sont écrits et l’équation chimique est équilibrée.

Équation ionique complète :

L’AgCl est un solide, il ne se décompose donc pas en ions en solution.

Equation ionique du réseau :

Tous les ions des spectateurs sont éliminés.

Vérifiez votre apprentissage 1.4.12 – Précipitations d’AgCl

Écrivez des équations ioniques nettes équilibrées pour décrire une réaction qui peut se produire lorsque K₂CO₃ et SrCl₂ sont mélangés.

Réponse

Sr²⁺ (aq) + CO₃^2- (aq)  →  SrCO₃ (s)

Exemple 1.4.15 – Combinaison de Na₂SO₄ et de NH₄I

Écrivez une équation ionique nette équilibrée pour décrire toute réaction qui se produit lorsque les solutions de Na₂SO₄ et de NH₄I sont mélangées.

Solution

Équation chimique complète :

Na₂SO₄ (aq) + NH₄I₂ (aq)  →  2 NaI (aq) + (NH₄)₂SO₄ (aq)

Les deux produits sont aqueux, il n’y a donc pas d’équation ionique nette qui puisse être écrite.

Vérifiez votre apprentissage 1.4.13 – Combinaison de Na₂SO₄ et de NH₄I

Écrivez une équation ionique nette équilibrée pour décrire une réaction qui peut se produire lorsque du FeSO₄ Ba(NO₃)₂ est mélangé.

Réponse

Ba²⁺ (aq) + SO₄^2- (aq)  →  BaSO₄ (s)

L’occurrence ou la non-occurrence de précipités peut être utilisée pour détecter la présence ou l’absence de diverses espèces en solution. Une solution de BaCl₂, par exemple, est souvent utilisée comme test pour détecter la présence de SO₄^2- ions. Il existe plusieurs sels insolubles de Ba, mais ils se dissolvent tous dans l’acide dilué, sauf le BaSO₄. Ainsi, si une solution de BaCl₂ est ajoutée à une solution inconnue qui a été préalablement acidifiée, l’apparition d’un précipité blanc est la preuve de la présence du SO₄^2- ion.

Figure 1.4.8. Les trois précipités communs d’halogénure d’argent : AgI, AgBr et AgCl (de gauche à droite). Les halogénures d’argent précipitent hors de la solution, mais forment souvent des suspensions avant de se déposer. Image utilisée avec autorisation (CC BY-SA 3.0 ; Cychr).

Les solutions d’AgNO₃ sont souvent utilisées de la même manière pour tester les ions halogénures. Si une solution d’AgNO₃ est ajoutée à une solution inconnue acidifiée, un précipité blanc indique la présence d’ions Cl^–, un précipité de couleur crème indique la présence d’ions Br^–, et un précipité jaune indique la présence d’ions I^– (figure 1.4.8). D’autres tests peuvent alors être effectués pour voir si un mélange de ces ions est présent. Lorsqu’on ajoute de l’AgNO₃ à l’eau du robinet, il se forme presque toujours un précipité blanc. Les ions Cl^– dans l’eau du robinet proviennent généralement du Cl₂ qui est ajouté aux réserves d’eau municipales pour tuer les micro-organismes.

Les précipités sont également utilisés pour l’analyse quantitative des solutions, c’est-à-dire pour déterminer la quantité de soluté ou la masse de soluté dans une solution donnée. À cette fin, il est souvent pratique d’utiliser le premier des trois types d’équations décrits ci-dessus. Ensuite, les règles de la stœchiométrie peuvent être appliquées.

Questions

★ Questions

1. Déterminez la molarité pour chacune des solutions suivantes :

a. 0,444 mole de CoCl₂ dans 0,654 L de solution

b. 98,0 g d’acide phosphorique, H₃PO₄, dans 1,00 L de solution

c. 0,2074 g d’hydroxyde de calcium, Ca(OH)₂, dans 40,00 ml de solution

d. 10,5 kg de Na₂SO₄•10H₂O dans 18,60 L de solution

e. 7,0 × 10^-3 mol de I2 dans 100,0 ml de solution

f. 1,8 × 10⁴ mg de HCl dans 0,075 L de solution

2. Réfléchissez à cette question : Quelle est la masse du soluté dans 0,500 L de glucose 0,30 M, C₆H₁₂O₆, utilisé pour l’injection intraveineuse ?

a. Indiquez les étapes nécessaires pour répondre à la question.

b. Répondez à la question.

3. Calculez le nombre de moles et la masse du soluté dans chacune des solutions suivantes :

a. 2,00 L de 18,5 mol/L H₂SO₄, acide sulfurique concentré

b. 100,0 ml de 3,8 × 10^-5 mol/L de NaCN, la concentration létale minimale de cyanure de sodium dans le sérum sanguin

c. 5,50 L de 13,3 mol/L H₂CO, le formaldéhyde utilisé pour “fixer” les échantillons de tissus

d. 325 ml de 1,8 × 10^-6 mol/L FeSO₄, la concentration minimale de sulfate de fer détectable par le goût dans l’eau potable

4. Réfléchissez à cette question : Quelle est la molarité du KMnO₄ dans une solution de 0,0908 g de KMnO₄ dans 0,500 L de solution ?

a. Indiquez les étapes nécessaires pour répondre à la question.

b. Répondez à la question.

5. Calculez la molarité de chacune des solutions suivantes :

a. 0,195 g de cholestérol, C₂₇H₄₆O, dans 0,100 L de sérum, soit la concentration moyenne de cholestérol dans le sérum humain

b. 4,25 g de NH₃ dans 0,500 L de solution, soit la concentration de NH₃ dans l’ammoniac domestique

c. 1,49 kg d’alcool isopropylique, C₃H₇OH, dans 2,50 L de solution, la concentration d’alcool isopropylique dans l’alcool à friction

d. 0,029 g de I₂ dans 0,100 L de solution, la solubilité de I₂ dans l’eau à 20 °C

6. Il y a environ 1,0 g de calcium, sous forme de Ca²⁺, dans 1,0 L de lait. Quelle est la molarité du Ca²⁺ dans le lait?

7. Un échantillon de 9,00 g contient 45,0 mg de sucre dissous. Quel est le pourcentage en masse de sucre dans cette solution ?

★★ Questions

8. Une solution de nettoyage est l’hypochlorite de sodium (eau de Javel) à 4 % en masse. Si vous utilisez 70 g de solution de nettoyage pour nettoyer votre salle de bain, quelle quantité d’eau de Javel a été utilisée ?

9. Votre bière contient 7% d’alcool par volume. Quelle quantité d’alcool pur avez-vous réellement consommée si votre bouteille contient 7 fl oz et que vous avez bu deux bouteilles et demie ?

10. Vous mélangez 73 μL de colorant de chargement avec 1000 μL d’ADN. Quelle quantité de colorant de charge se trouve dans la solution en pourcentage du volume.

11. Votre taux de glycémie est de 0,2 % (m/v). Combien de grammes de sucre y a-t-il dans votre corps (en supposant que vous ayez 5,1 litres de sang) ?

12. Supposons que le vinaigre que vous utilisez est de 0,76 mol/L d’acide acétique (CH₃COOH). Quelle est la concentration de votre vinaigre en ppm?

13. Supposons que vous mélangez 50 ml de CoCl₂ dans 0,654 L de solution. Quelle est la concentration du mélange résultant en ppb ?

14. Vous ajoutez 3,6 g de H₂SO₄ à 10,0 g d’eau. Quelle est la molalité de cette solution ?

15. Vous disposez d’un litre de solution saline (NaCl) à 0,15 mol/L. Quelle est la molalité de la solution si NaCl a une densité de 2,16 g/cm³ (indice : 1cm³ = 1 mL) ?

16. Si l’on dilue 4,12 L d’une solution de H₃PO₄ à 0,850 mol/L pour obtenir un volume de 10,00 L, quelle est la concentration de la solution obtenue ?

★ Questions (partie 2)

17. Quelle est la concentration finale de la solution produite lorsqu’on laisse s’évaporer 225,5 ml d’une solution de Na₂CO₃ à 0,09988 mol/L jusqu’à ce que le volume de la solution soit réduit à 45,00 ml ?

18. Une expérience dans un laboratoire de chimie générale nécessite une solution de HCl à 2,00 mol/L. Combien de ml de HCl 11,9 mol/L serait nécessaire pour obtenir 250 ml de HCl 2,00 mol/L ?

19. Écrivez l’équation chimique complète, l’équation ionique complète et l’équation ionique nette pour le mélange de Ca(NO₃)₂ (aq) et de H₃PO₄ (aq).

20. Écrivez l’équation chimique complète, l’équation ionique complète et l’équation ionique nette pour le mélange de KCl (aq) et de Pb(NO₃)₂ (aq).

21. Indiquez le ou les types de réaction que représente chacun des éléments suivants :

a. Ca (s) + Br₂ (l)  ⟶  CaBr₂ (s)

b. Ca(OH)₂ (aq) + 2 HBr (aq)  ⟶  CaBr₂ (aq) + 2 H₂O (l)

c. C₆H₁₂ (l) + 9 O₂ (g)  ⟶  6 CO_{2 (}g) + 6 H₂O (g)

Réponses

1. (a) 0,679 mol/L ; (b) 1,00 mol/L ; (c) 0,06998 mol/L ; (d) 1,75 mol/L ; (e) 0,070 mol/L ; (f) 6,6 mol/L

2. a) déterminer le nombre de moles de glucose dans 0,500 L de solution ; déterminer la masse molaire du glucose ; déterminer la masse du glucose à partir du nombre de moles et de sa masse molaire ; b) 27 g

3. (a) 37,0 mol H₂SO₄ ; 3,63 x 10³ g H₂SO₄ ; (b) 3,8 × 10^-6 mol NaCN ; 1,9 × 10^-4 g NaCN ; (c) 73,2 mol H₂CO ; 2,20 kg H₂CO ; (d) 5,9 × 10^-7 mol FeSO₄ ; 8,9 × 10^-5 g FeSO₄

4. (a) Déterminer la masse molaire de KMnO4 ; déterminer le nombre de moles de KMnO4 dans la solution ; à partir du nombre de moles et du volume de la solution, déterminer la molarité ; (b) 1,15 × 10^-3 mol/L

5. (a) 5,04 × 10^-3 mol/L ; (b) 0,499 mol/L ; (c) 9,92 mol/L ; (d) 1,1 × 10^-3 mol/L

6. 0,025 mol/L

7. 0.5%

8. 2.8 g

9. 36,23 ml

10. 6.8%

11. 1,02 kg

12. 45719,97 ppm

13. 71 022 727 ppb

14. 3,67 mol/kg

15. 0,069 mol/kg

16. 0,35 mol/L

17. 0,50 mol/L

18. 42 ml

19. Complète : 3 Ca(NO₃)₂ + 2 H₃PO₄  →  Ca₃(PO₄)₂ + 6 HNO₃, Ionique complète : 3 Ca²⁺ + 6 NO₃^– + 6 H + 2 PO₄^3-  →  Ca₃(PO₄)₂ + 6 H + 6 NO₃^– , Net Ionic : 3 Ca²⁺ + 2 PO₄^3-  →  Ca₃(PO4)₂

20. Complète : Pb(NO₃)₂ (aq) + 2 KI (aq)  →  PbI₂ (s) + 2 KNO₃ (aq), Ionique complète : Pb²⁺ (aq) + 2 NO₃^–(aq) + 2 K⁺ (aq) + 2 I^– (aq)  →  PbI₂ (aq) + 2 K⁺ (aq) + 2 NO₃^–(aq), Net Ionic : Pb²⁺ (aq) + 2 I^– (aq)  →  PbI₂ (aq)

21. (a) oxydation-réduction (addition) ; (b) acide-base (neutralisation) ; (c) oxydation-réduction (combustion)