1.3 – Stœchiométrie des réactions

La stœchiométrie des équations chimiques équilibrées

Une équation chimique équilibrée fournit une grande quantité d’informations dans un format très bref. Les formules chimiques fournissent l’identité des réactifs et des produits impliqués dans le changement chimique, permettant ainsi la classification de la réaction. Les coefficients fournissent les nombres relatifs de ces espèces chimiques, permettant une évaluation quantitative des relations entre les quantités de substances consommées et produites par la réaction. Ces relations quantitatives sont connues sous le nom de stœchiométrie de la réaction, un terme dérivé des mots grecs stoicheion (signifiant “élément”) et metron (signifiant “mesure”). Dans ce module, l’utilisation d’équations chimiques équilibrées pour diverses applications stœchiométriques est explorée.

L’approche générale de l’utilisation des relations stœchiométriques est similaire dans son concept à la façon dont les gens s’adonnent à de nombreuses activités communes. La préparation des aliments, par exemple, offre une comparaison appropriée. Une recette pour faire huit crêpes nécessite une tasse de mélange à crêpes, ¾ une tasse de lait et un œuf. L'”équation” représentant la préparation des crêpes selon cette recette est :

1 tasse de mélange + ¾ tasse de lait + 1 œuf  →  8 crêpes

Si deux douzaines de crêpes sont nécessaires pour un grand petit-déjeuner familial, les quantités d’ingrédients doivent être augmentées proportionnellement en fonction des quantités indiquées dans la recette. Par exemple, le nombre d’œufs nécessaire pour faire 24 crêpes est de

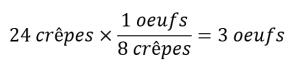
Les équations chimiques équilibrées sont utilisées à peu près de la même manière pour déterminer la quantité d’un réactif nécessaire pour réagir avec une quantité donnée d’un autre réactif, ou pour obtenir une quantité donnée de produit, et ainsi de suite. Les coefficients de l’équation équilibrée sont utilisés pour dériver des facteurs stœchiométriques qui permettent de calculer la quantité souhaitée. Pour illustrer cette idée, considérons la production d’ammoniac par la réaction de l’hydrogène et de l’azote :

N₂ (g) + 3 H₂ (g)  →  2 NH₃ (g)

Cette équation montre que les molécules d’ammoniac sont produites à partir de molécules d’hydrogène dans un rapport de 2:3, et que les facteurs stœchiométriques peuvent être dérivés en utilisant n’importe quelle unité de quantité (nombre) :

Ces facteurs stœchiométriques peuvent être utilisés pour calculer le nombre de molécules d’ammoniac produites à partir d’un nombre donné de molécules d’hydrogène, ou le nombre de molécules d’hydrogène nécessaires pour produire un nombre donné de molécules d’ammoniac. Des facteurs similaires peuvent être dérivés pour toute paire de substances dans toute équation chimique.

Exemple 1.3.1 – Moles de réactif requises dans une réaction

Combien de moles d’I₂ sont nécessaires pour réagir avec 0,429 mole d’Al selon l’équation suivante (voir figure 1.3.1) ?

2 Al + 3 I₂  →  2 AlI₃

Figure 1.3.1. L’aluminium et l’iode réagissent pour produire de l’iodure d’aluminium. La chaleur de la réaction vaporise une partie de l’iode solide sous forme de vapeur violette. (crédit : modification des travaux de Mark Ott)

Solution

En se référant à l’équation chimique équilibrée, le facteur stœchiométrique reliant les deux substances d’intérêt est de 3 mol I₂, 2 mol Al. La quantité molaire d’iode est obtenue en multipliant la quantité molaire d’aluminium fournie par ce facteur :

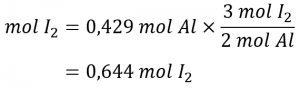
Vérifiez votre apprentissage 1.3.1 – Moles de réactif requises dans une réaction

Combien de moles de Ca(OH)₂ sont nécessaires pour réagir avec 1,36 mole de H₃PO₄ pour produire du Ca₃(PO₄)₂ selon l’équation 3 Ca(OH)₂ + 2 H₃PO₄  ⟶  Ca₃(PO₄)₂ + 6 H₂O ?

Réponse

2.04 mol

Exemple 1.3.2 – Nombre de molécules de produit générées par une réaction

Selon cette équation, combien de molécules de dioxyde de carbone sont produites lors de la combustion de 0,75 mole de propane ?

C₃H₈ + 5 O₂  →  3 CO₂ + 4 H₂O

Solution

L’approche ici est la même que pour l’exemple précédent, bien que le nombre absolu de molécules soit demandé, et non le nombre de moles de molécules. Il faudra simplement utiliser le facteur de conversion des moles en nombres, le nombre d’Avogadro.

L’équation équilibrée montre que le dioxyde de carbone est produit à partir du propane dans un rapport de 3:1 :

En utilisant ce facteur stœchiométrique, la quantité molaire de propane fournie et le nombre d’Avogadro,

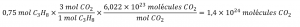
Vérifiez votre apprentissage 1.3.2 – Nombre de molécules de produit générées par une réaction

Combien de molécules NH₃ sont produites par la réaction de 4,0 moles de Ca(OH)₂ selon l’équation suivante :

(NH₄)₂SO₄ + Ca(OH)₂  →  2 NH₃ + CaSO₄ + 2 H₂O

Réponse

4,8 × 10²⁴ molécules de NH₃

Ces exemples illustrent la facilité avec laquelle les quantités de substances impliquées dans une réaction chimique de stœchiométrie connue peuvent être liées. Cependant, mesurer directement le nombre d’atomes et de molécules n’est pas une tâche facile, et l’application pratique de la stœchiométrie exige que nous utilisions la propriété plus facilement mesurable de la masse.

Exemple 1.3.3 – Relier les masses de réactifs et de produits

Quelle masse d’hydroxyde de sodium, NaOH, serait nécessaire pour produire 16 g de lait antiacide de magnésie [hydroxyde de magnésium, Mg(OH)₂] par la réaction suivante ?

MgCl₂ (aq) + 2 NaOH(aq)  →  Mg(OH)₂ (s) + 2 NaCl (aq)

Solution

Nous devons dériver un facteur stœchiométrique approprié de l’équation chimique équilibrée et l’utiliser pour mettre en relation les quantités des deux substances d’intérêt. Dans ce cas, cependant, les masses (et non les quantités molaires) sont fournies et demandées, de sorte que des étapes supplémentaires du type de celles apprises dans le chapitre précédent sont nécessaires. Les calculs nécessaires sont décrits dans ce diagramme:

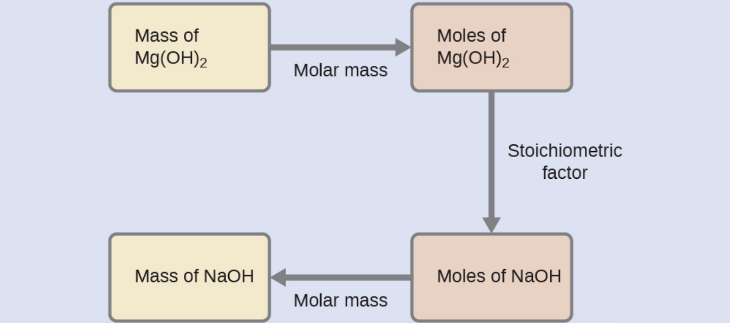
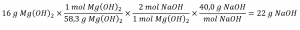
Vérifiez votre apprentissage 1.3.3 – Relier les masses de réactifs et de produits

Quelle masse d’oxyde de gallium, Ga₂O₃, peut-on préparer à partir de 29,0 g de gallium métallique ? L’équation de la réaction est 4 Ga + 3 O₂ ⟶ 2 Ga₂O₃.

Réponse

39,0 g

Exemple 1.3.4 – Relier les masses de réactifs

Quelle masse d’oxygène gazeux, O₂, de l’air est consommée lors de la combustion de 702 g d’octane, C₈H₁₈, l’un des principaux composants de l’essence ?

2 C₈H₁₈ + 25 O₂  →  16 CO₂ + 18 H₂O

Solution

L’approche requise ici est la même que pour l’exemple précédent, à la seule différence que les masses fournies et demandées concernent toutes deux des espèces réactives. 

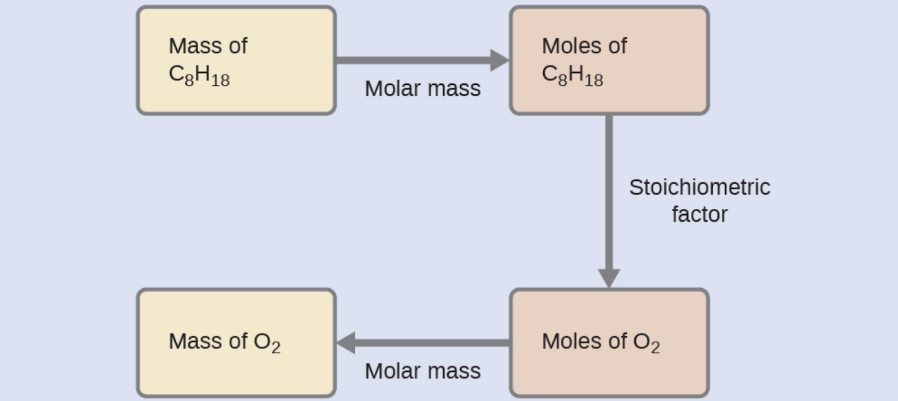
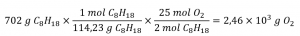
Vérifiez votre apprentissage 1.3.4 – Relier les masses de réactifs

Quelle est la masse de CO nécessaire pour réagir avec 25,13 g de Fe₂O₃ selon l’équation :

Fe₂O₃ + 3 CO  ⟶  2 Fe + 3 CO₂ ?

Réponse

13,22 g

Ces exemples illustrent quelques cas de calculs de stœchiométrie de réaction. De nombreuses variations des étapes de calcul de début et de fin sont possibles en fonction des quantités particulières fournies et recherchées (volumes, concentrations des solutions, etc.). Indépendamment des détails, tous ces calculs partagent un élément essentiel commun : l’utilisation de facteurs stœchiométriques dérivés d’équations chimiques équilibrées. La figure 1.3.2 donne un aperçu général des différentes étapes de calcul associées à de nombreux calculs de stœchiométrie des réactions.

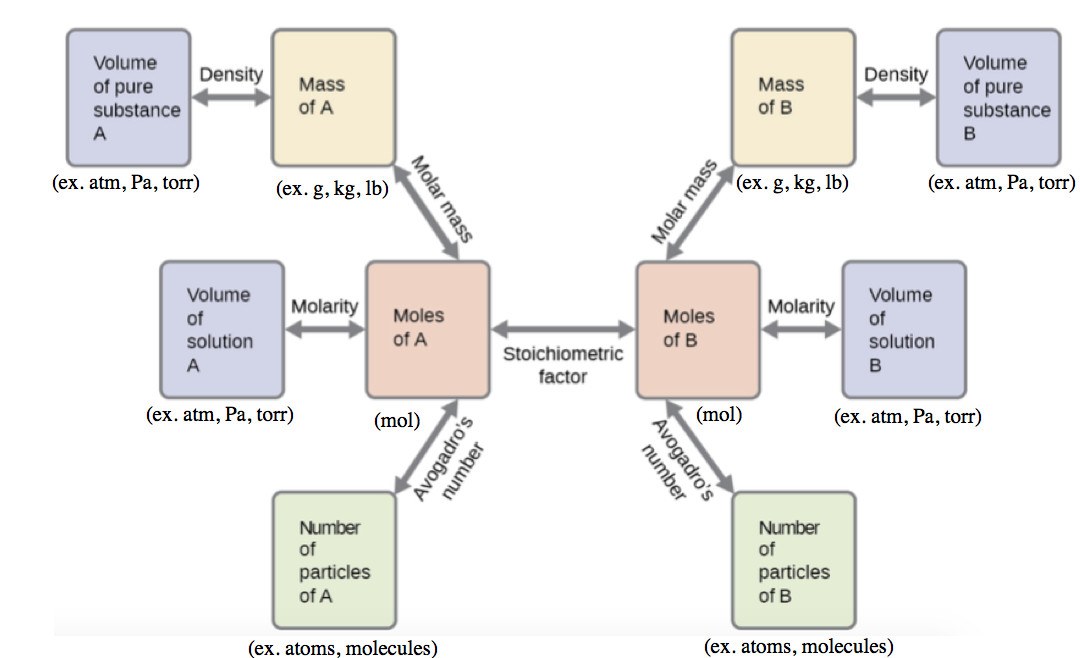
Figure 1.3.2. L’organigramme décrit les différentes étapes de calcul impliquées dans la plupart des calculs de stœchiométrie de réaction.

Limiter les réactifs

Considérons une autre analogie alimentaire, celle des sandwiches au fromage grillé (figure 1.3.3) :

1 tranche de fromage + 2 tranches de pain → 1 sandwich

Les quantités stœchiométriques des ingrédients des sandwiches pour cette recette sont des tranches de pain et de fromage dans un rapport de 2:1. Avec 28 tranches de pain et 11 tranches de fromage, on peut préparer 11 sandwichs selon la recette fournie, en utilisant tout le fromage fourni et en ayant six tranches de pain restantes. Dans ce scénario, le nombre de sandwiches préparés a été limité par le nombre de tranches de fromage, et les tranches de pain ont été fournies en excès.

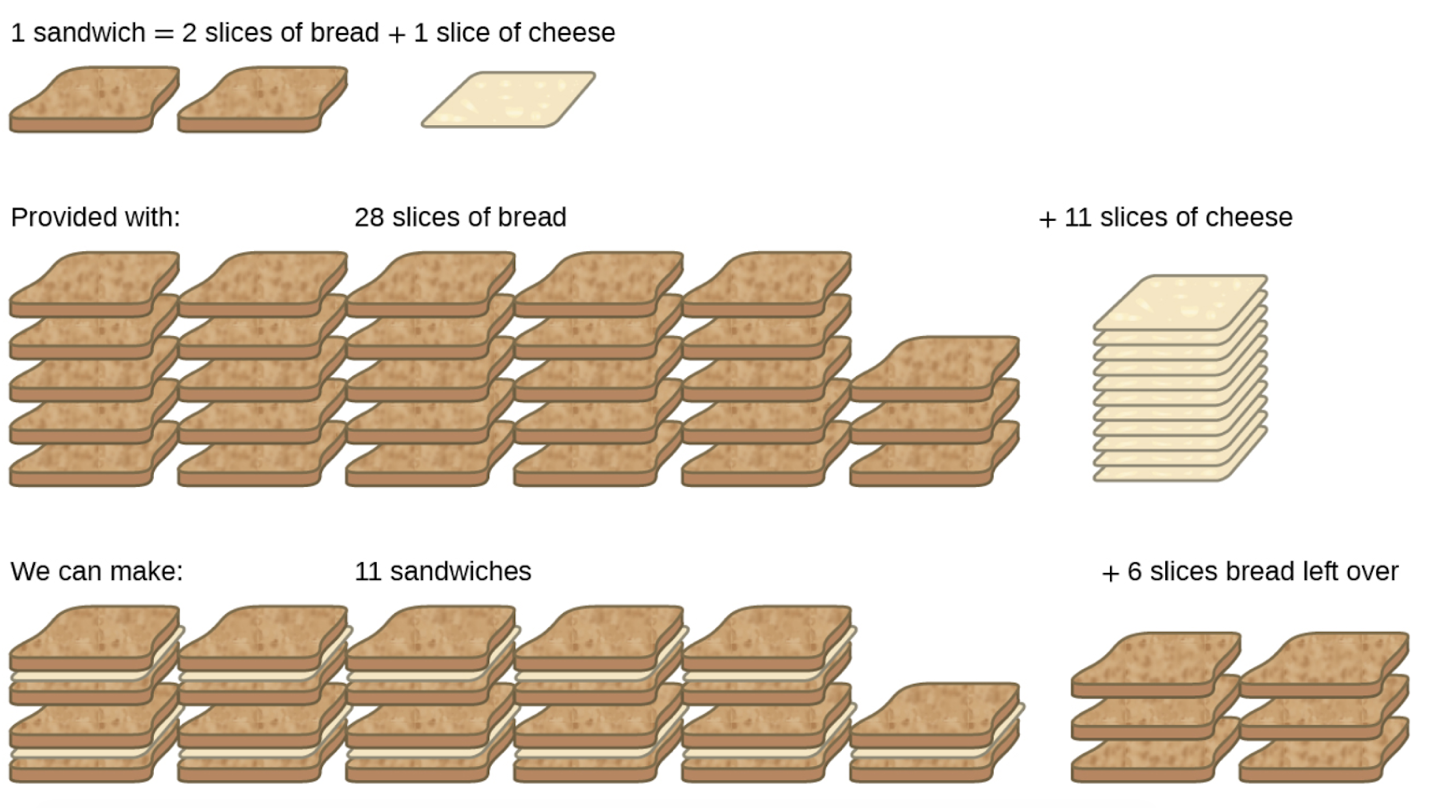
Figure 1.3.3. La fabrication de sandwichs peut illustrer les concepts de réactifs limitants et excédentaires.

Considérons maintenant ce concept par rapport à un processus chimique, la réaction de l’hydrogène avec le chlore pour produire du chlorure d’hydrogène :

H₂ (g) + Cl₂ (g)  →  2 HCl (g)

L’équation équilibrée montre que l’hydrogène et le chlore réagissent dans un rapport stœchiométrique de 1:1. Si ces réactifs sont fournis en d’autres quantités, l’un des réactifs sera presque toujours entièrement consommé, ce qui limite la quantité de produit pouvant être générée. Cette substance est le réactif limitant, et l’autre substance est le réactif en excès. Pour identifier les réactifs limitants et en excès dans une situation donnée, il faut calculer les quantités molaires de chaque réactif fourni et les comparer aux quantités stœchiométriques représentées dans l’équation chimique équilibrée. Par exemple, imaginez que vous combinez 3 moles de H₂ et 2 moles de Cl₂. Cela représente un rapport de 3:2 (ou 1,5:1) de l’hydrogène au chlore présent pour la réaction, qui est supérieur au rapport stœchiométrique de 1:1. L’hydrogène est donc présent en excès, et le chlore est le réactif limitant. Lorsque tout le chlore fourni réagit (2 mol), la réaction consommera 2 mol des 3 mol d’hydrogène fournies, laissant 1 mol d’hydrogène non réagi.

Une autre approche pour identifier le réactif limitant consiste à comparer la quantité de produit attendue pour la réaction complète de chaque réactif. La quantité de chaque réactif est utilisée pour calculer séparément la quantité de produit qui serait formée selon la stœchiométrie de la réaction. Le réactif qui donne la plus petite quantité de produit est le réactif limitant. Dans l’exemple du paragraphe précédent, la réaction complète de l’hydrogène donnerait

La réaction complète du chlore fourni produirait

Le chlore sera complètement consommé une fois que 4 moles de HCl auront été produites. Comme l’hydrogène a été fourni en quantité suffisante pour produire 6 moles de HCl, il restera de l’hydrogène n’ayant pas réagi une fois cette réaction terminée. Le chlore est donc le réactif limitant et l’hydrogène est le réactif en excès (figure 1.3.4).

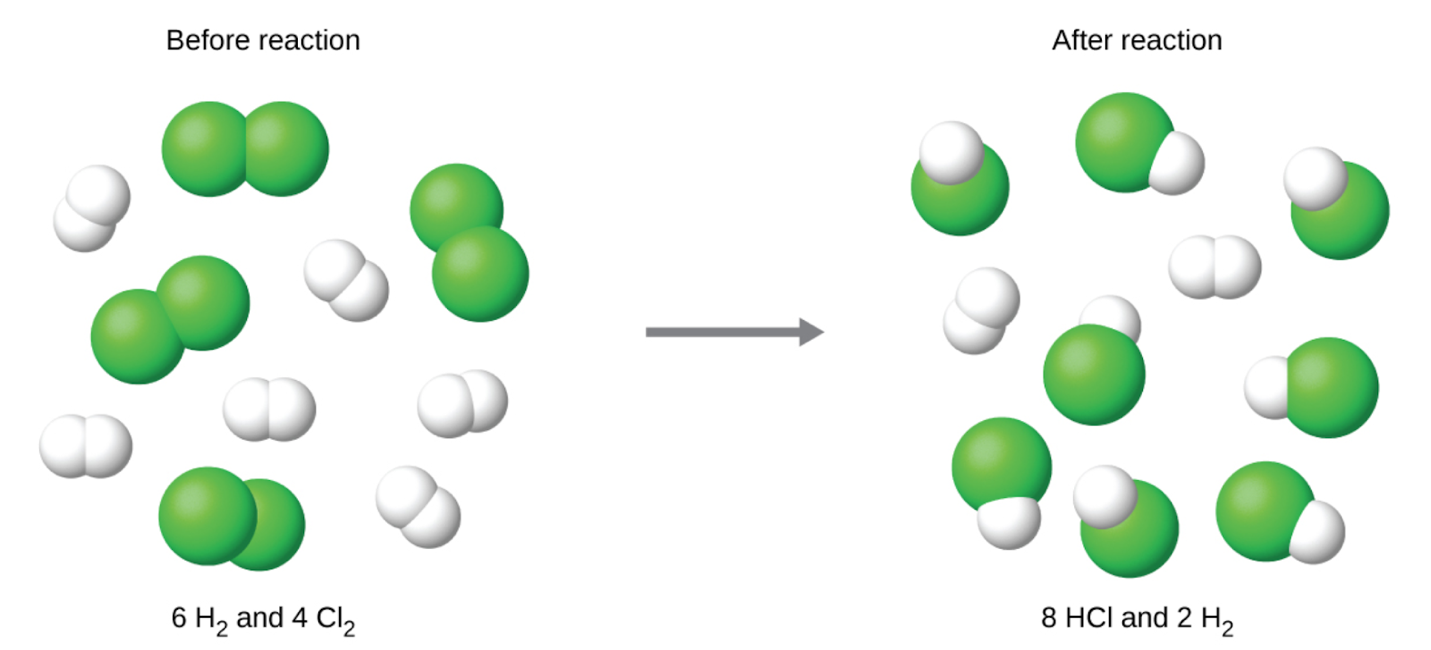
Figure 1.3.4. Lorsque H₂ et Cl₂ sont combinés en quantités non–stœchiométriques, l’un de ces réactifs limitera la quantité de HCl pouvant être produite. Cette illustration montre une réaction dans laquelle l’hydrogène est présent en excès et le chlore est le réactif limitant.

Exemple 1.3.5 – Identification du réactif limitant

Le nitrure de silicium est une céramique très dure et résistante aux hautes températures, utilisée comme composant des aubes de turbine des moteurs à réaction. Il est préparé selon l’équation suivante :

3 Si (s) + 2 N₂ (g) → Si₃N₄ (s) 

Quel est le réactif limitant lorsque 2,00 g de Si et 1,50 g de N₂ réagissent ?

Solution

Calculer les quantités molaires de réactifs fournies, puis comparer ces quantités à l’équation équilibrée pour identifier le réactif limitant.

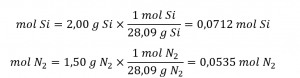
Le rapport molaire Si : N₂ fourni est :

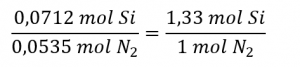
Le rapport stœchiométrique Si : N₂ est :

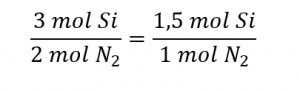
La comparaison de ces rapports montre que le Si est fourni en quantité inférieure à la quantité stœchiométrique, tout comme le réactif limitant. On peut aussi calculer la quantité de produit attendue pour la réaction complète de chacun des réactifs fournis. Les 0,0712 moles de silicium donneraient

alors que les 0,0535 moles d’azote produiraient

Comme le silicium donne une quantité moindre de produit, il est le réactif limitant.

Vérifiez votre apprentissage 1.3.5 – Identification du réactif limitant

  1. Quel est le réactif limitant lorsque 5,00 g de H₂ et 10,0 g d’O₂ réagissent et forment de l’eau ?

  2. Quelle quantité de réactif reste-t-il une fois la réaction terminée ?

Réponse

  1. O₂

  2. 3,75 g

Pourcentage de rendement

La quantité de produit qui peut être produite par une réaction dans des conditions spécifiées, calculée selon la stœchiométrie d’une équation chimique correctement équilibrée, est appelée le rendement théorique de la réaction. En pratique, la quantité de produit obtenue est appelée rendement réel, et elle est souvent inférieure au rendement théorique pour un certain nombre de raisons. Certaines réactions sont intrinsèquement inefficaces, étant accompagnées de réactions secondaires qui génèrent d’autres produits. D’autres sont, par nature, incomplètes (voir les réactions partielles des acides et des bases faibles évoquées plus haut dans ce chapitre). Certains produits sont difficiles à collecter sans perte, de sorte qu’une récupération moins que parfaite réduira le rendement réel. La mesure dans laquelle le rendement théorique d’une réaction est atteint est généralement exprimée en pourcentage de rendement :

Les rendements réels et théoriques peuvent être exprimés en masses ou en quantités molaires (ou toute autre propriété appropriée ; par exemple, le volume, si le produit est un gaz). Tant que les deux rendements sont exprimés en utilisant les mêmes unités, ces unités s’annulent lorsque le pourcentage de rendement est calculé.

Exemple 1.3.6 – Calcul du pourcentage de rendement

En faisant réagir 1,274 g de sulfate de cuivre avec un excès de zinc métallique, on obtient 0,392 g de cuivre métallique selon l’équation :

CuSO₄ (aq) + Zn (s)  →  Cu (s) + ZnSO₄ (aq)

Quel est le pourcentage de rendement ?

Solution

L’information fournie identifie le sulfate de cuivre comme le réactif limitant, et donc le rendement théorique est trouvé par l’approche illustrée dans le module précédent, comme montré ici :

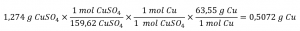
En utilisant ce rendement théorique et la valeur fournie pour le rendement réel, le pourcentage de rendement est calculé comme suit

Vérifiez votre apprentissage 1.3.6 – Calcul du pourcentage de rendement

Vous utilisez la réaction suivante pour produire du fréon (CF₂Cl₂) à partir de CCl₄ et de HF :

CCl₄ + 2 HF  →  CF₂Cl₂ + 2 HCl 

Cette réaction a un rendement de 75 %. Sachant cela, quelle quantité de HF (en kg) est nécessaire pour produire 10 kg de fréon ?

Réponse

4,40 kg

Questions

★ Questions

1. Rédigez l’équation équilibrée, puis décrivez les étapes nécessaires pour déterminer les informations demandées dans chacun des cas suivants :

a. Le nombre de moles (en mol) et la masse de chlore (en grammes), Cl₂, nécessaires pour réagir avec 10,0 g de sodium métallique, Na, pour produire du chlorure de sodium, NaCl.

b. Le nombre de moles (en mol) et la masse (en grammes) d’oxygène formée par la décomposition de 1,252 g d’oxyde de mercure (II).

c. Le nombre de moles (en mol) et la masse (en grammes) de nitrate de sodium, NaNO₃, nécessaires pour produire 128 g d’oxygène. (NaNO₂ est l’autre produit).

d. Le nombre de moles (en mol) et la masse (en grammes) de dioxyde de carbone formés par la combustion de 20,0 kg de carbone en excès d’oxygène.

e. Le nombre de moles (en mol) et la masse (en grammes) de carbonate de cuivre(II) nécessaires pour produire 1.500 kg d’oxyde de cuivre(II). (L’autre produit est le CO₂).

f. Le nombre de moles et la masse de C₂H₄Br₂ formée par la réaction de 12,85 g d’éthène avec un excès de Br₂.

2. I₂ est produit par la réaction de 0,4235 mole de CuCl₂ selon l’équation suivante :

2 CuCl₂ + 4 KI  →  2 CuI + 4 KCl + I₂

a. Combien de molécules d’I₂ sont produites ?

b. Quelle est la masse de I₂ produite (en grammes) ?

3. L’argent est souvent extrait de minerais tels que le K[Ag(CN)₂], puis récupéré par la réaction

2 K[Ag(CN)₂] (aq) + Zn (s)  →  2 Ag (s) + Zn(CN)₂ (aq) + 2 KCN (aq)

a. Combien de molécules de Zn(CN)₂ sont produites par la réaction de 35,27 g de K[Ag(CN)₂] ?

b. Quelle est la masse de Zn(CN)₂ produite (en grammes) ?

4. Le carborundum est le carbure de silicium, SiC, un matériel très dur utilisé comme abrasif sur le papier de verre et dans d’autres applications. Il est préparé par la réaction de sable pur, SiO₂, avec du carbone à haute température. Le monoxyde de carbone, CO, est l’autre produit de cette réaction. Écrivez l’équation équilibrée de la réaction et calculez la quantité (masse, en grammes) de SiO₂ nécessaire pour produire 3,00 kg de SiC.

★★ Questions

5. Lors d’un accident, une solution contenant 2,5 kg d’acide nitrique a été déversée. Deux kilogrammes de Na₂CO₃ ont été rapidement répandus sur la zone et du CO₂ a été libéré par la réaction. A-t-on utilisé suffisamment de Na₂CO₃ pour neutraliser tout l’acide ?

6. Un échantillon de 0,53 g de dioxyde de carbone a été obtenu en chauffant 1,31 g de carbonate de calcium. Quel est le rendement en pourcentage de cette réaction?

CaCO₃ (s)  →  CaO (s) + CO₂ (s)

7. Le fréon-12, CCl₂F₂, est préparé à partir du CCl₄ par réaction avec le HF. L’autre produit de cette réaction est le HCl. Décrivez les étapes nécessaires pour déterminer le pourcentage de rendement d’une réaction qui produit 12,5 g de CCl₂F₂ à partir de 32,9 g de CCl₄. Le fréon-12 a été interdit et n’est plus utilisé comme réfrigérant car il catalyse la décomposition de l’ozone et a une très longue durée de vie dans l’atmosphère. Déterminez le pourcentage de rendement.

8. L’acide citrique, C₆H₈O₇, un composant des confitures, gelées et boissons gazeuses fruitées, est préparé industriellement par la fermentation du saccharose par la moisissure Aspergillus niger. L’équation représentant cette réaction est la suivante

C₁₂H₂₂O₁₁ + H₂O + 3 O₂  →  2 C₆H₈O₇ + 4 H₂O

Quelle masse d’acide citrique (en grammes) est produite à partir d’exactement 1 tonne (1 000 × 10³ kg) de saccharose si le rendement est de 92,30 % ?

9. Décrivez les étapes nécessaires pour déterminer le réactif limitant lorsque 30,0 g de propane, C₃H₈, sont brûlés avec 75,0 g d’oxygène. Déterminer le réactif limitant.

10. Quel est le réactif limitant lorsque 1,50 g de lithium et 1,50 g d’azote se combinent pour former du nitrure de lithium, un composant des batteries avancées, selon l’équation déséquilibrée suivante ?

Li + N₂  →  Li₃N

11. L’uranium peut être isolé de ses minerais en le dissolvant sous forme d’UO₂(NO₃)₂, puis en le séparant sous forme d’UO₂(C₂O₄)∙3 H₂O solide. L’addition de 0,4031 g d’oxalate de sodium, Na₂C₂O₄, à une solution contenant 1,481 g de nitrate d’uranyle, UO₂(NO₃)_2, donne 1,073 g d’UO₂(C₂O₄)∙3 H₂O solide.

Na₂C₂O₄ + UO₂(NO₃)₂ + 3 H₂O  →  UO₂(C₂O₄)∙3H₂O + 2 NaNO₃

Déterminer le réactif limitant et le pourcentage de rendement de cette réaction.

12. Le pentoxyde de phosphore utilisé pour produire l’acide phosphorique des boissons gazeuses à base de cola est préparé par la combustion du phosphore dans l’oxygène.

a. Quel est le réactif limitant lorsque 0,200 mol de P₄ et 0,200 mol d’O₂ réagissent selon

P₄ + 5 O₂  ⟶  P₄O₁₀

b. Calculer le pourcentage de rendement si 10,0 g de P₄O₁₀ sont isolés de la réaction.

Réponses

1. (a) Cl₂ (g) + 2 Na (s)  →  2 NaCl (aq), 0,435 mol Na, 0,217 mol Cl₂, 15,4 g Cl₂ ; (b) 2 HgO (s)  →  2 Hg (s) + O₂ (g), 0.005780 mol HgO, 2,890 × 10^-3 mol O₂, 9,248 × 10^-2 g O₂ ; (c) 2 NaNO₃ (s)  →  O₂ (g) + 2 NaNO₂ (s), 8.00 mol NaNO₃, 6,8 × 10² g NaNO₃ ; (d) C (s) + O₂ (g)  →  CO₂ (g), 1665 mol CO₂, 73,3 kg CO₂ ; (e) CuCO₃ (s)  →  CuO (s) + CO₂ (g), 18,86 mol CuO, 2,330 kg CuCO₃ ; (f) C₂H₄Br₂  →  C₂H₄ + Br₂, 0,4580 mol C₂H₄Br₂, 86,05 g C₂H₄Br₂

2. (a) 1,28 × 10²³ molécules ; (b) 26,9 g

3. (a) 5,337 × 10²² molécules ; (b) 10,41 g Zn(CN)₂

4. 4,50 kg SiO₂, SiO₂ + 3 C  →  SiC + 2 CO

5. Oui – reconnaître qu’il y a un rapport molaire de 2:1 de HNO₃ : Na₂CO₃ dans l’équation chimique équilibrée pour cette réaction de neutralisation. Il faut donc au moins 2 moles de Na₂CO₃ pour chaque mole de HNO₃ pour neutraliser tout l’acide. Les quantités données (en kg) correspondent à des quantités molaires de 39,67 moles de HNO₃ : 18,87 moles de Na₂CO₃ ; c’est un rapport de 2:1 mole (2X plus de carbonate de sodium que d’acide). Par conséquent, une quantité suffisante de Na₂CO₃ a été utilisée pour neutraliser tout l’acide.

6. 92.0 %

7. Pourcentage de rendement = 48,3 %, g CCl₄ ⟶ mol CCl₄ ⟶ mol CCl₂F₂ ⟶ g CCl₂F₂

8. 1,03 tonnes

9. (1) Déterminer l’équation chimique équilibrée : C₃H₆ + 5 O₂  →  3 CO₂ + 4 H₂O ; (2) En utilisant les masses données et la masse molaire des réactifs, trouvez les moles pour le propane et l’oxygène ; (3) Avec les moles trouvées dans l’étape précédente, trouvez la quantité de moles de dioxyde de carbone avec les rapports molaires basés sur l’équation chimique équilibrée ; (4) Avec ces deux valeurs, déterminez la masse de dioxyde de carbone. Le réactif qui donne la plus petite masse de dioxyde de carbone est le réactif limitant. Dans ce cas, il s’agit de l’oxygène.

10. Li est le réactif limitant

11. Na₂C₂O₄ est le réactif limitant. Pourcentage de rendement = 86,6 %.

12. (a) O₂ est le réactif limitant ; (b) 88 %.