1.1 – La mole

La mole

L’identité d’une substance est définie non seulement par les types d’atomes ou d’ions qu’elle contient, mais aussi par la quantité de chaque type d’atome ou d’ion. Par exemple, l’eau, H₂O_, et le peroxyde d’hydrogène, H₂O₂, se ressemblent en ce sens que leurs molécules respectives sont composées d’atomes d’hydrogène et d’oxygène. Cependant, comme une molécule de peroxyde d’hydrogène contient deux atomes d’oxygène, contrairement à la molécule d’eau qui n’en a qu’un, les deux substances présentent des propriétés très différentes. Aujourd’hui, nous possédons des instruments sophistiqués qui permettent de mesurer directement ces caractéristiques microscopiques déterminantes ; cependant, les mêmes caractéristiques ont été à l’origine dérivées de la mesure de propriétés macroscopiques (les masses et les volumes des quantités de matière en vrac) à l’aide d’outils relativement simples (balances et verrerie volumétrique). Cette approche expérimentale a nécessité l’introduction d’une nouvelle unité pour la quantité de substances, la mole, qui reste indispensable dans la chimie moderne.

La mole est une unité de quantité similaire aux unités familières comme la paire, la douzaine, le brut, etc. Elle fournit une mesure spécifique du nombre d’atomes ou de molécules dans un échantillon global de matière. Une mole est définie comme la quantité de substance contenant le même nombre d’entités discrètes (telles que des atomes, des molécules et des ions) que le nombre d’atomes dans un échantillon de ¹²C pur pesant exactement 12 g. Pour illustrer davantage cette idée, 1 paire = 2 choses, 1 douzaine = 12 choses et 1 mole = 6,022 × 10²³ choses. Une connotation latine du mot “mole” est “grande masse” ou “volume”, ce qui est cohérent avec son utilisation comme nom pour cette unité. La mole établit un lien entre une propriété macroscopique facilement mesurable, la masse volumique, et une propriété fondamentale extrêmement importante, le nombre d’atomes, de molécules, etc.

Le nombre d’entités composant une mole a été déterminé expérimentalement comme étant 6,02214179 × 10²³, une constante fondamentale appelée nombre d'Avogadro (N_A) ou constante d’Avogadro en l’honneur du scientifique italien Amedeo Avogadro. Cette constante est correctement rapportée avec une unité explicite de “par mole,” une version arrondie étant 6,022 × 10²³/mol.

Conformément à sa définition en tant qu’unité de quantité, une mole de tout élément contient le même nombre d’atomes qu’une mole de tout autre élément. Les masses d’une mole de différents éléments sont cependant différentes, car les masses des différents atomes sont radicalement différentes. La masse molaire d’un élément (ou d’un composé) est la masse en grammes d’une mole de cette substance, une propriété exprimée en unités de grammes par mole (g/mol) (voir figure 1.1.1).

Figure 1.1.1 Chaque échantillon contient 6,022 × 10²³ atomes – 1,00 mole d’atomes. De gauche à droite (rangée du haut) : 65,4 g de zinc, 12,0 g de carbone, 24,3 g de magnésium et 63,5 g de cuivre. De gauche à droite (rangée du bas) : 32,1 g de soufre, 28,1 g de silicium, 207 g de plomb et 118,7 g d’étain. (crédit : modification du travail de Mark Ott)

Comme les définitions de la mole et de l’unité de masse atomique sont basées sur la même substance de référence, le ¹²C, la masse molaire de toute substance est numériquement équivalente à son poids atomique ou à sa formule en unités de masse atomique, ou amu. Selon la définition de l’amu, un seul atome de ¹²C pèse 12 amu (sa masse atomique est de 12 amu). Selon la définition de la mole, 12 g de ¹²C contient 1 mole d’atomes de ¹²C (sa masse molaire est de 12 g/mol). Cette relation est valable pour tous les éléments puisque leur masse atomique est mesurée par rapport à celle de la substance de référence de l’amu, le ¹²C. Suivant ce principe, la masse molaire d’un composé en grammes est également numériquement équivalente à sa masse de formule en amu (figure 1.1.2).

Figure 1.1.2 Chaque échantillon contient 6,02 × 10²³ molécules ou unités de formule – 1,00 mole du composé ou de l’élément. Dans le sens des aiguilles d’une montre, à partir du coin supérieur gauche : 130,2 g de C₈H₁₇OH (1-octanol, masse de formule 130,2 amu), 454,4 g de HgI₂ (iodure de mercure (II), masse de formule 454,4 amu), 32,0 g de CH₃OH (méthanol, masse de formule 32,0 amu) et 256,5 g de S₈ (soufre, masse de formule 256,5 amu). (crédit : Sahar Atwa)

Tableau 1.1.1 Propriétés quantitatives des éléments sélectionnés

Si la masse atomique et la masse molaire sont numériquement équivalentes, il faut garder à l’esprit qu’elles sont très différentes en termes d’échelle, comme le montre la grande différence de magnitude de leurs unités respectives (amu contre g). Pour apprécier l’énormité de la mole, considérez une petite goutte d’eau pesant environ 0,03 g (voir figure 1.1.3). Bien que cela ne représente qu’une infime fraction d’une mole d’eau (~18 g), elle contient plus de molécules d’eau qu’on ne peut l’imaginer. Si les molécules étaient réparties de manière égale entre les sept milliards de personnes sur Terre, chaque personne recevrait plus de 100 milliards de molécules.

Figure 1.1.3. Le nombre de molécules dans une seule goutte d’eau est environ 100 milliards de fois supérieur au nombre de personnes sur terre. (crédit : “tanakawho“/Wikimedia commons)

Les relations entre la masse de la formule, la mole et le nombre d’Avogadro peuvent être appliquées pour calculer diverses quantités qui décrivent la composition des substances et des composés. Par exemple, si nous connaissons la masse et la composition chimique d’une substance, nous pouvons déterminer le nombre de moles et calculer le nombre d’atomes ou de molécules dans l’échantillon. De même, si nous connaissons le nombre de moles d’une substance, nous pouvons en déduire le nombre d’atomes ou de molécules et calculer la masse de la substance.

Exemple 1.1.1 – Déterminer le nombre de moles à partir des grammes d’un élément

Selon les directives nutritionnelles du ministère américain de l’agriculture, les besoins quotidiens moyens en potassium alimentaire sont estimés à 4,7 g. Quel est le besoin moyen quotidiens estimé en potassium en moles ?

Solution

La masse de K est fournie, et la quantité correspondante de K en moles est demandée. En se référant au tableau périodique, la masse atomique de K est de 39,10 amu, et donc sa masse molaire est de 39,10 g/mol. La masse donnée de K (4,7 g) est un peu plus d’un dixième de la masse molaire (39,10 g), de sorte qu’une estimation “approximative” raisonnable du nombre de moles serait légèrement supérieure à 0,1 mole.

La quantité molaire d’une substance peut être calculée en divisant sa masse (g) par sa masse molaire (g/mol) :

La méthode factorielle soutient cette approche mathématique puisque l’unité (et non la dimension, car la même variable est exprimée selon une méthode différente mais exprimant essentiellement les mêmes données) “g” s’annule et la réponse comporte des unités de “mol” :

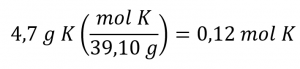
La quantité calculée (0,12 mol K) est conforme à nos attentes approximatives puisqu’elle est un peu plus grande que 0,1 mol.

Vérifiez votre apprentissage 1.1.1 – Déterminer le nombre de moles à partir des grammes d’un élément

Le béryllium est un métal léger utilisé pour fabriquer des fenêtres transparentes pour les rayons X des instruments d’imagerie médicale. Combien de moles de Be y a-t-il dans une fenêtre à feuille mince pesant 3,24 g ?

Réponse

0,360 mol

Exemple 1.1.2 – Déterminer les grammes à partir de moles pour un élément

Un litre d’air contient 9,2 × 10^-4 mol d’argon. Quelle est la masse de Ar dans un litre d’air ?

Solution

La quantité molaire de Ar est fournie et doit être utilisée pour calculer la masse correspondante en grammes. Comme la quantité de Ar est inférieure à 1 mole, la masse sera inférieure à la masse d’une mole de Ar, soit environ 40 g. La quantité molaire en question est approximativement un millième (~10^-3) d’une mole, et la masse correspondante devrait donc être approximativement un millième de la masse molaire (~0,04 g) :

Dans ce cas, la logique dicte (et la méthode des facteurs d’étiquetage l’appuie) de multiplier la quantité fournie (mol) par la masse molaire (g/mol) :

Le résultat est en accord avec nos attentes, autour de 0,04 g Ar.

Vérifiez votre apprentissage 1.1.2 – Déterminer les grammes à partir de moles pour un élément

Quelle est la masse de 2 561 moles d’or ?

Réponse

504,4 g

Exemple 1.1.3 – Calcul du nombre d’atomes à partir de la masse pour un élément

Le cuivre est couramment utilisé pour fabriquer des fils électriques (figure 1.1.4.). Combien d’atomes de cuivre y a-t-il dans 5,00 g de fil de cuivre ?

Figure 1.1.4. Le fil de cuivre est composé de nombreux, nombreux atomes de Cu. (crédit : Emilian Robert Vicol)

Solution

Le nombre d’atomes de Cu dans le fil peut être dérivé de sa masse par un calcul en deux étapes : d’abord le calcul de la quantité molaire de Cu, puis l’utilisation du nombre d’Avogadro (N_A) pour convertir cette quantité molaire en nombre d’atomes de Cu :

Étant donné que la masse de l’échantillon fourni (5,00 g) est un peu inférieure à un dixième de la masse d’une mole de Cu (~64 g), une estimation raisonnable du nombre d’atomes dans l’échantillon serait de l’ordre d’un dixième de N_A, soit environ 1022 atomes de Cu. La réalisation du calcul en deux étapes donne des résultats :

La méthode factorielle d’étiquetage donne l’annulation souhaitée des unités, et le résultat calculé est de l’ordre de 10²² comme prévu.

Vérifiez votre apprentissage 1.1.3 – Calcul du nombre d’atomes à partir de la masse pour un élément

Un prospecteur qui cherche de l’or dans une rivière recueille 15,00 g d’or pur. Combien y a-t-il d’atomes d’Au dans cette quantité d’or ?

Réponse

4,586 × 10²² atomes d’Au

Exemple 1.1.4 – Déterminer les moles à partir des grammes pour un composé

Notre corps synthétise des protéines à partir d’acides aminés. L’un de ces acides aminés est la glycine, dont la formule moléculaire est C₂H₅O₂N. Combien de moles de molécules de glycine sont contenues dans 28,35 g de glycine ?

Solution

Nous pouvons déduire le nombre de moles d’un composé à partir de sa masse en suivant la même procédure que celle utilisée pour un élément :

La masse molaire de la glycine est nécessaire pour ce calcul, et elle est calculée de la même manière que sa masse moléculaire. Une mole de glycine, C₂H₅O₂N, contient 2 moles de carbone, 5 moles d’hydrogène, 2 moles d’oxygène et 1 mole d’azote :

La masse de glycine fournie (~28 g) est un peu plus d’un tiers de la masse molaire (~75 g/mol), on s’attendrait donc à ce que le résultat calculé soit un peu plus d’un tiers de mole (~0,33 mol). En divisant la masse du composé par sa masse molaire, on obtient le résultat :

Ce résultat est conforme à notre estimation approximative.

Vérifiez votre apprentissage 1.1.4 – Déterminer les moles à partir des grammes pour un composé

Combien de moles de saccharose, C₁₂H₂₂O₁₁, se trouvent dans un échantillon de 25 g de saccharose ?

Réponse

0,073 mol

Exemple 1.1.5 – Déterminer les grammes à partir des moles pour un composé

La vitamine C est un composé covalent dont la formule moléculaire est C₆H₈O₆. L’apport alimentaire quotidien recommandé en vitamine C pour les enfants âgés de 4 à 8 ans est de 1,42 × 10^-4 mol. Quelle est la masse de cet apport en grammes?

Solution

Comme pour les éléments, la masse d’un composé peut être dérivée de sa quantité molaire comme indiqué :

La masse molaire de ce composé est calculée à 176,124 g/mol. Le nombre de moles donné est une très petite fraction de mole (~10^-4 ou un dix millième) ; par conséquent, on s’attendrait à ce que la masse correspondante soit environ un dix millième de la masse molaire (~0,02 g). En effectuant le calcul, nous obtenons :

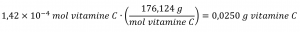
Cela correspond au résultat escompté.

Vérifiez votre apprentissage 1.1.5 – Déterminer les grammes à partir des moles pour un composé

Quelle est la masse de 0,443 mole d’hydrazine, N₂H₄ ?

Réponse

14,2 g

Exemple 1.1.6 – Déterminer le nombre d’atomes et de molécules à partir de la masse d’un composé

Un sachet d’édulcorant artificiel contient 40,0 mg de saccharine (C₇H₅NO₃S), dont la structure est la suivante

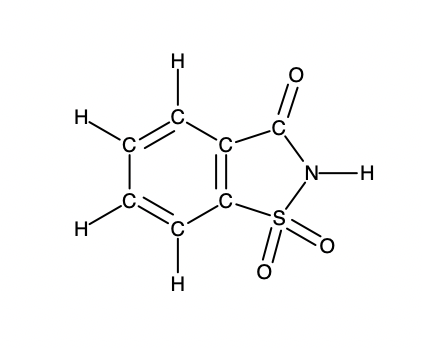
Étant donné que la saccharine a une masse molaire de 183,18 g/mol, combien de molécules de saccharine y a-t-il dans un échantillon de 40,0 mg (0,0400 g) de saccharine ? Combien d’atomes de carbone se trouvent dans le même échantillon ?

Solution

Le nombre de molécules dans une masse donnée d’un composé est calculé en dérivant d’abord le nombre de moles, puis en le multipliant par le nombre d’Avogadro :

Utilisation de la masse et de la masse molaire fournies pour les rendements en saccharine :

La formule du composé montre que chaque molécule contient sept atomes de carbone, et donc le nombre d’atomes de C dans l’échantillon fourni :

Vérifiez votre apprentissage 1.1.6 – Déterminer le nombre d’atomes et de molécules à partir de la masse d’un composé

Combien de molécules de C₄H₁₀ sont contenues dans 9,213 g de ce composé ? Combien d’atomes d’hydrogène ?

Réponse

9,545 × 10²² molécules C₄H₁₀ ; 9,545 × 10²³ atomes H

Composition en pourcentage

La composition élémentaire d’un composé définit son identité chimique, et les formules chimiques sont la façon la plus succincte de représenter cette composition élémentaire. Lorsque la formule d’un composé est inconnue, la mesure de la masse de chacun de ses éléments constitutifs est souvent la première étape du processus de détermination expérimentale de la formule. Les résultats de ces mesures permettent de calculer la composition en pourcentage du composé, définie comme le pourcentage en masse de chaque élément du composé. Prenons par exemple un composé gazeux composé uniquement de carbone et d’hydrogène. La composition en pourcentage de ce composé pourrait être représentée comme suit :

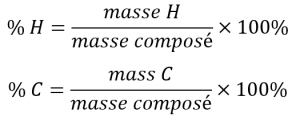
Si l’analyse d’un échantillon de 10,0 g de ce gaz montrait qu’il contient 2,5 g de H et 7,5 g de C, la composition en pourcentage serait calculée comme étant de 25 % de H et 75 % de C :

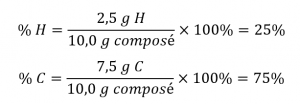
Un composé chimique est la combinaison de deux ou plusieurs éléments. Si vous étudiez un composé chimique, vous voudrez peut-être trouver le pourcentage de composition d’un certain élément dans ce composé chimique. L’équation pour la composition en pourcentage est la suivante :

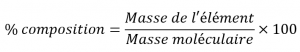
Si vous voulez connaître le pourcentage de composition des éléments d’un composé, suivez ces étapes :

Les étapes de la résolution :

1. Trouvez la masse molaire de tous les éléments du composé en grammes par mole.

2. Trouvez la masse moléculaire de l’ensemble du composé.

3. Divisez la masse molaire du composant par la masse moléculaire totale.

4. Vous avez maintenant un nombre entre 0 et 1, multipliez-le par 100 pour obtenir le pourcentage de composition !

Conseils pour résoudre les problèmes :

1. Les composés s’additionneront toujours à 100%, donc dans un composé binaire, vous pouvez trouver le pourcentage du premier élément, puis soustraire de 100% pour déterminer le pourcentage du second élément.

2. Si vous utilisez une calculatrice, vous pouvez stocker la masse molaire globale dans une variable telle que “A”. Cela accélérera les calculs et réduira les erreurs typographiques.

Ces étapes sont décrites dans la figure ci-dessous.

Étapes à suivre pour déterminer la composition en pourcentage

(avec exemple)

PCl₅ Pentachlorure de phosphore

1. Trouver la masse molaire de tous les éléments du composé

P = 30,974 g

Cl = 5 (35,453 g) = 177,265 g

2. Trouvez la masse moléculaire :

PCl₅ = 30,974 g + 177,265 g = 208,239 g

3. Divisez chaque masse molaire par la masse moléculaire et multipliez par 100 :

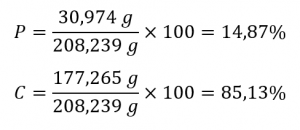
Par conséquent, le pentachlorure de phosphore contient 14,87 % de P et 85,13 % de Cl en masse.

Exemple 1.1.7 – Étapes à suivre pour déterminer la composition en pourcentage

Trouvez la composition en pourcentage de l’acide chlorhydrique (HCl).

Solution

Trouvez d’abord la masse molaire de l’hydrogène. H = 1,00794 g. Trouvez maintenant la masse moléculaire de HCl : 1,00794 g + 35,4527 g = 36,46064 g. Suivez les étapes 3 et 4 : (1,00794 g/36,46064 g) x 100 = 2,76 %. Maintenant, il suffit de soustraire pour trouver le pourcentage en masse de chlore dans le composé : 100 % – 2,76 % = 97,24 %. Par conséquent, HCl est constitué de 2,76 % d’hydrogène et de 97,24 % de chlore en masse.

Questions

★ Questions

1. Comparez 1 mole de H₂, 1 mole de O₂ et 1 mole de F₂. Quelle est la molécule qui a le plus grand nombre de molécules ? Expliquez pourquoi.

2. Lequel contient la plus grande masse d’oxygène : 0,75 mole d’éthanol (C₂H₅OH), 0,60 mole d’acide formique (HCO₂H) ou 1,0 mole d’eau (H₂O) ? Expliquez pourquoi.

3. En quoi la masse moléculaire et la masse molaire d’un composé sont-elles similaires et en quoi sont-elles différentes ?

4. Calculez la masse molaire (en g/mol) de chacun des éléments suivants :

a. L’halothane anesthésique, C₂HBrClF₃

b. L’herbicide paraquat, C₁₂H₁₄N₂Cl₂

c. Caféine, C₈H₁₀N₄O₂

d. Urée, CO(NH₂)₂

e. Un savon typique, C₁₇H₃₅CO₂Na

5. Déterminez le nombre de moles du composé et le nombre de moles (en mol) de chaque type d’atome dans chacun des cas suivants :

a. 25,0 g de propylène, C₃H₆

b. 3,06 ｘ10^-3 g de l’acide aminé glycine, C₂H₅NO₂

c. 25 lb de l’herbicide Treflan, C₁₃H₁₆N₂O₄F (1 lb = 454 g)

d. 0,125 kg de l’insecticide Paris Green, Cu₄(AsO₃)₂(CH₃CO₂)₂

e. 325 mg d’aspirine, C₆H₄(CO₂H)(CO₂CH₃)

6. Déterminez la masse (en grammes) de chacun des éléments suivants :

a. 0,0146 mol KOH

b. 10,2 mol d’éthane, C₂H₆

c. 1,6 x 10^-3 mol Na₂SO₄

d. 6,854 x 10³ mol de glucose, C₆H₁₂O₆

e. 2,86 mol Co(NH3)₆Cl₃

★★ Questions

7. Une portion de 55 grammes d’une céréale donnée fournit 270 mg de sodium, soit 11 % de l’apport quotidien recommandé. Combien de moles et d’atomes de sodium sont présents dans l’apport journalier recommandé ?

8. Une certaine céréale croquante aux noix contient 11,0 grammes de sucre (saccharose, C₁₂H₂₂O₁₁) par portion de 60,0 grammes. Combien de portions de cette céréale faut-il consommer pour obtenir 0,0278 mole de sucre ?

9. Lequel des éléments suivants représente le plus petit nombre de molécules ?

a. 20,0 g de H₂O (18,02 g/mol)

b. 77,0 g de CH₄ (16,06 g/mol)

c. 68,0 g de CaH₂ (42,09 g/mol)

d. 100,0 g de N₂O (44,02 g/mol)

e. 84,0 g de HF (20,01 g/mol)

Réponses

1. Comme il y a 1 mole de chaque, ils ont tous le même nombre de molécules.

2. Acide formique. Sa formule comporte deux fois plus d’atomes d’oxygène que les deux autres composés (un chacun). Par conséquent, 0,60 mole d’acide formique équivaudrait à 1,20 mole d’un composé contenant un seul atome d’oxygène.

3. Les deux masses ont la même valeur numérique, mais les unités sont différentes : la masse moléculaire est la masse d’une molécule tandis que la masse molaire est la masse de 6,022 × 10²³ molécules.

4. (a) 197,382 g/mole ; (b) 257,163 g/mole ; (c) 194,193 g/mole ; (d) 60,056 g/mole ; (e) 306,464 g/mole

5. (a) 0,594 mol C₃H₆, 1,78 mol C, 3,56 mol H ; (b) 4,08 × 10^-5 mol C₂H₅NO₂, 8,15 × 10^-5 mol C, 2,04 × 10^-4 mol H, 4,08 × 10^-5 mol N, 8,15 × 10^-5 mol O ; (c) 40,06 mol C₁₃H₁₆N₂O₄F, 520,79 mol C, 640,98 mol H, 80.12 mol N, 160,24 mol O, 40,06 mol F ; (d) 0,202 mol Cu₄(AsO₃)₂(CH₃CO₂)_2, 0,81 mol Cu, 0,40 mol As, 2,02 mol O, 0,81 mol C, 1,21 mol H ; (e) 1,80 × 10^-3 mol C₆H₄(CO₂H)(CO₂CH₃), 0,016 mol C, 0,014 H, 7,22 × 10^-3 mol O

6. (a) 0,819 g ; (b) 307 g ; (c) 0,23 g ; (d) 1,235 × 10⁶ g (1235 kg) ; (e) 765 g

7. 0,107 mol Na, 6,43 × 10²² atomes Na

8. 0,865 portion, soit environ 1 portion.

9. 20,0 g H₂O représente le plus petit nombre de molécules puisqu’il a le plus petit nombre de moles.