8.2 Price and Quantity in Perfect Competition
A perfectly competitive firm has only one major decision to make — namely, what quantity to produce. To understand this, consider a different way of writing out the basic definition of profit:
Profit = Total Revenue – Total Cost
= Price × Quantity – Average Total Cost × Quantity
Since a perfectly competitive firm must accept the price for its output as determined by the product’s market demand and supply, it cannot choose the price it charges. This is already determined in the profit equation, and so the perfectly competitive firm can sell any number of units at exactly the same price. It implies that the firm faces a perfectly elastic demand curve for its product: buyers are willing to buy any number of units of output from the firm at the market price. When the perfectly competitive firm chooses what quantity to produce, then this quantity — along with the prices prevailing in the market for output and inputs — will determine the firm’s total revenue, total costs, and ultimately, level of profits.
Determining the Highest Profit by Comparing Total Revenue and Total Cost
A perfectly competitive firm can sell as large a quantity as it wishes, as long as it accepts the prevailing market price. The formula above shows that total revenue depends on the quantity sold and the price charged. If the firm sells a higher quantity of output, then total revenue will increase. If the market price of the product increases, then total revenue also increases whatever the quantity of output sold.
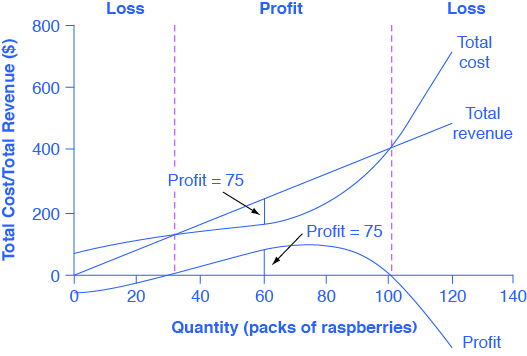
The table in 8.3 is represented graphically in Fig 8.2 which shows the total revenue and total costs for the raspberry farm. The horizontal axis shows the quantity of frozen raspberries produced in packs. The vertical axis shows both total revenue and total costs, measured in dollars. The total cost curve intersects with the vertical axis at a value that shows the level of fixed costs and then slopes upward. All these cost curves follow the same characteristics as the curves that we covered in the chapter on Production and Cost.
| Price | Quantity | Total Revenue | Marginal Revenue |
|---|---|---|---|
| $4 | 1 | $4 | - |
| $4 | 2 | $8 | $4 |
| $4 | 3 | $12 | $4 |
| $4 | 4 | $16 | $4 |
Fig 8.3
From Fig 8.2, the vertical gap between total revenue and the total cost is profit, for example, at Q = 60, TR = 240 and TC = 165. The difference is 75, which is the height of the profit curve at that output level. The firm doesn’t make a profit at every level of output. In this example, total costs will exceed total revenues at output levels from 0 to approximately 30, and so over this range of output, the firm will be making losses. At output levels from 40 to 100, total revenues exceed total costs, so the firm is earning profits. However, at any output greater than 100, total costs again exceed total revenues and the firm is making increasing losses.
From the table in Fig 8.3, we can calculate the economic profit by subtracting total costs from total revenue. Total profits appear in the final column of Fig 8.3. Maximum profit occurs at an output between 70 and 80 when profit equals $90.
Attribution
“8.2 How Perfectly Competitive Firms Make Output Decisions” in Principles of Economics 2e by OpenStax Rice University is licensed under Creative Commons Attribution 4.0 International License.

