11.7 Sequential Game

A “Sequential Game” between 2 or more players one where players take turns.

To solve a Sequential Game, we need to use a Decision Tree, as shown in Fig 11.4, not a payoff matrix.

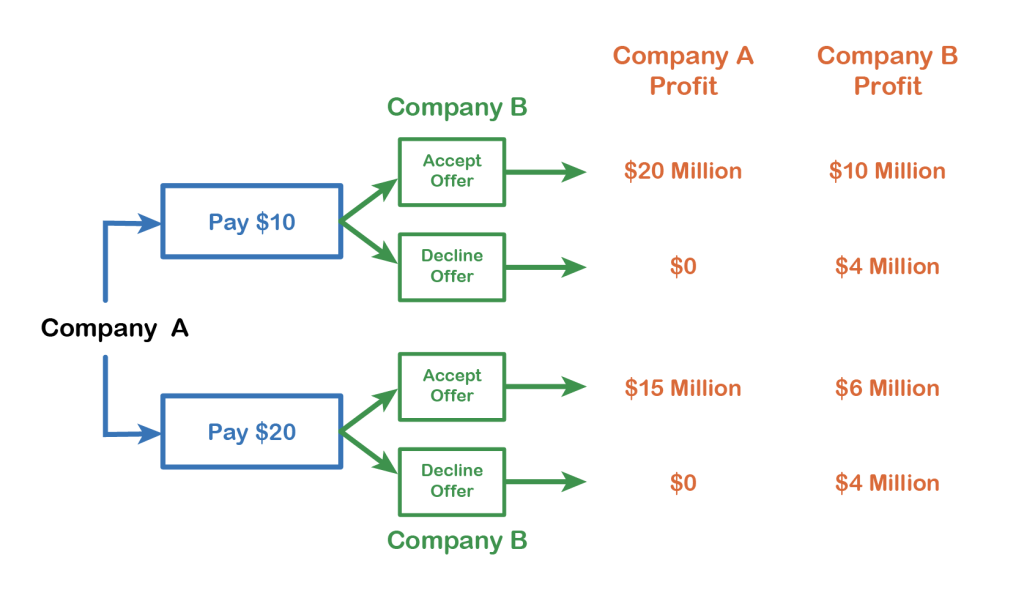
To solve a sequential game, we use backwards induction. Since the second player will make the final decision we need to determine which choice they will make. To do this, we consider both choices for player A and choose the optimal choice for player B (i.e.: for Pay $10, Player B can Accept and make 10 mill or Decline and make 4 mill; in this case 10 mill is optimal so they would always choose to accept the offer if $10 was the choice by player A).

We complete this for all options of player A (i.e.: for Pay $20, Player B will also accept and make 10 mill instead of declining and only making 4 mill). Once we have determined what Player B will do, Player A can then pick from those remaining options and choose what is best for them (i.e.: Player A can choose Pay $10 and make 20 million or Pay $20 and make 15 million; they would choose the 20 mill). Therefore, the equilibrium would be Player A chooses to Pay $10 and Player B will Accept Offer.

Attribution

10.2 Oligopoly” in Principles of Economics 2e by OpenStax is licensed under Creative Commons Attribution 4.0 International License.

“Prisoner’s Dilemma” in Microeconomics by Lumen Learning is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.