9.5 Statistical Inference for Two Population Proportions
LEARNING OBJECTIVES
- Construct and interpret a confidence interval for two population proportions.
- Conduct and interpret hypothesis tests for two population proportions.
Similar to comparing two population means, the comparison of two population proportions is very common. Often, we want to find out if the two populations under study have the same proportion or if there is some difference in the two population proportions. Unlike two population means, we can only approach the comparison of two population proportions using independent samples. Recall that two populations are independent if the sample taken from population 1 is not related in anyway to the sample taken from population 2. In this situation, any relationship between the samples or populations is entirely coincidental.
Throughout this section, we will use subscripts to identify the values for the proportions and sample sizes for the two populations:
| Symbol for: | Population 1 | Population 2 |
| Population Proportion | [latex]p_1[/latex] | [latex]p_2[/latex] |
| Sample Size | [latex]n_1[/latex] | [latex]n_2[/latex] |
| Sample Proportion | [latex]\hat{p}_1[/latex] | [latex]\hat{p}_2[/latex] |
| Number of Items in Sample with Characteristic of Interest | [latex]x_1[/latex] | [latex]x_2[/latex] |
In order to construct a confidence interval or conduct a hypothesis test on the difference in two population proportions ([latex]p_1-p_2[/latex]), we need to use the distribution of the difference in the sample proportions [latex]\hat{p}_1-\hat{p}_2[/latex]:
- The mean of the distribution of the difference in the sample proportions is [latex]\displaystyle{\mu_{\hat{p}_1-\hat{p}_2}}=p_1-p_2[/latex].
- The standard deviation of the distribution of the difference in the sample proportions is [latex]\displaystyle{\sigma_{\hat{p}_1-\hat{p}_2}=\sqrt{\frac{p_1\times(1-p_1)}{n_1}+\frac{p_2\times(1-p_2)}{n_2}}}[/latex].
- The distribution of the difference in the sample proportions is normal if [latex]n_1\times p_1\geq 5[/latex], [latex]n_1\times(1-p_1)\geq 5[/latex], [latex]n_2 \times p_2 \geq 5[/latex] and [latex]n_2\times(1-p_2)\geq 5[/latex].
- Assuming the distribution of the difference of the sample proportions is normal, the [latex]z[/latex]-score is [latex]\displaystyle{z=\frac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{\sqrt{\frac{p_1\times(1-p_1)}{n_1}+\frac{p_2\times(1-p_2)}{n_2}}}}[/latex].
Constructing a Confidence Interval for the Difference in Two Population Proportions
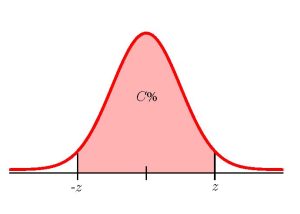
Suppose a sample of size [latex]n_1[/latex] with sample proportion [latex]\hat{p}_1[/latex] is taken from population 1 and a sample of size [latex]n_2[/latex] with sample proportion [latex]\hat{p}_2[/latex] is taken from population 2. The limits for the confidence interval with confidence level [latex]C[/latex] for the difference in the population proportions [latex]\displaystyle{p_1-p_2}[/latex] are:
[latex]\begin{eqnarray*}\\\text{Lower Limit}&=&\hat{p}_1-\hat{p}_2-z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p_2}\times(1-\hat{p}_2)}{n_2}}\\\\\text{Upper Limit}&=&\hat{p}_1-\hat{p}_2+z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p_2}\times(1-\hat{p}_2)}{n_2}}\\\\\end{eqnarray*}[/latex]
where [latex]z[/latex] is the positive [latex]z[/latex]-score of the standard normal distribution so that the area under the curve in between [latex]-z[/latex] and [latex]z[/latex] is [latex]C\%[/latex].
NOTES
- In order to construct the confidence interval for the difference in two population proportions, we need to check that the normal distribution applies. This means that we need to check that [latex]n_1\times p_1\geq 5[/latex], [latex]n_1\times(1-p_1)\geq 5[/latex], [latex]n_2 \times p_2 \geq 5[/latex] and [latex]n_2\times(1-p_2)\geq 5[/latex].
- Because the population proportions [latex]p_1[/latex] and [latex]p_2[/latex] are often unknown, we replace the values of the population proportions with the sample proportions [latex]\hat{p}_1[/latex] and [latex]\hat{p}_2[/latex] in the normal distribution check. That is, when the population proportions are unknown, we check [latex]n_1\times\hat{p}_1\geq 5[/latex], [latex]n_1 \times (1-\hat{p}_1) \geq 5[/latex], [latex]n_2\times\hat{p}_2\geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex] to verify that the normal distribution applies.
CALCULATING THE [latex]{\color{white}{z}}[/latex]-SCORE FOR A CONFIDENCE INTERVAL IN EXCEL
To find the [latex]z[/latex]-score to construct a confidence interval with confidence level [latex]C[/latex], use the norm.s.inv(area to the left of z) function.
- For area to the left of z, enter the entire area to the left of the [latex]z[/latex]-score you are trying to find. For a confidence interval, the area to the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
The output from the norm.s.inv function is the value of the [latex]z[/latex]-score needed to construct the confidence interval.
NOTE
The norm.s.inv function requires that we enter the entire area to the left of the unknown [latex]z[/latex]-score. This area includes the confidence level (the area in the middle of the distribution) plus the remaining area in the left tail.
EXAMPLE
A marketing company places an advertisement for a new brand of deodorant on two different platforms: television and social media. The company wants to study the proportion of people who remembered seeing the advertisement two hours later. In a sample of 200 people who saw the advertisement on television, 74 remembered seeing it two hours later. In a sample of 300 people who saw the advertisement on social media, 129 remembered seeing it two hours later.
- Construct a 98% confidence interval for the difference in the proportion of people from the two different platforms that remember seeing the advertisement two hours later.
- Interpret the confidence interval found in part 1.
- Is there evidence to suggest that the proportion of people from social media who remember seeing the advertisement two hours later is greater than the proportion of people from television? Explain.
Solution:
- Let television be population 1 and social media be population 2. From the question we have the following information:
Television Social Media [latex]n_1=200[/latex] [latex]n_2=300[/latex] [latex]\hat{p}_1=\frac{74}{200}=0.37[/latex] [latex]\hat{p}_2=\frac{129}{300}=0.43[/latex] Before constructing the confidence interval, we check that the normal distribution applies:
[latex]\begin{eqnarray*}n_1\times\hat{p}_1&=&200\times 0.37=74\geq 5\\n_1\times(1-\hat{p}_1)&=&200\times(1-0.37)=126\geq 5\\n_2\times\hat{p}_2&=&300\times 0.43=129\geq 5\\n_2\times(1-\hat{p}_1)&=&300\times(1-0.37)=171\geq 5\end{eqnarray*}[/latex]
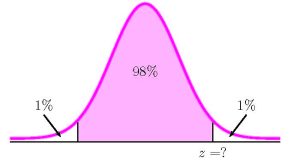
To find the confidence interval, we need to find the [latex]z[/latex]-score for the 98% confidence interval. This means that we need to find the [latex]z[/latex]-score so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.98+\frac{1-0.98}{2}=0.99}[/latex].
Function norm.s.inv Answer Field 1 0.99 2.3263… So [latex]z=2.3263...[/latex]. The 98% confidence interval is
[latex]\begin{eqnarray*}\\\text{Lower Limit}&=&\hat{p}_1-\hat{p}_2-z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p_2}\times(1-\hat{p}_2)}{n_2}}\\&=&0.37-0.43-2.3263...\times\sqrt{\frac{0.37\times(1-0.37)}{200}+\frac{0.43\times(1-0.43)}{300}}\\&=&-0.1636\\\\\text{Upper Limit}&=&\hat{p}_1-\hat{p}_2+z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p_2}\times(1-\hat{p}_2)}{n_2}}\\&=&0.37-0.43+2.3263...\times\sqrt{\frac{0.37\times(1-0.37)}{200}+\frac{0.43\times(1-0.43)}{300}}\\&=&0.0436\\\\\end{eqnarray*}[/latex]
- We are 98% confident that the difference in the proportion of people from the two platforms that remember seeing the advertisement two hours later is between -16.36% and 4.36%.
- Because 0 is inside the confidence interval, it suggests that the difference in the proportions [latex]\displaystyle{p_1-p_2}[/latex] is 0. That is, [latex]\displaystyle{p_1-p_2=0}[/latex]. This suggests that the two proportions are equal. So the proportion of people from social media who remember seeing the advertisement two hours is not greater than the proportion of people from television.
NOTES
- Because the population proportions are unknown, we use the sample proportions in the check for normality.
- When calculating the limits for the confidence interval keep all of the decimals in the [latex]z[/latex]-score and other values throughout the calculation. This will ensure that there is no round-off error in the answers. You can use Excel to do the calculation of the limits, clicking on the cell containing the [latex]z[/latex]-score and any other values, to ensure that all of the decimal places are used in the calculation.
- The limits for the confidence interval are percents. For example, the upper limit of 0.0436 is the decimal form of a percent: 4.36%.
- When writing down the interpretation of the confidence interval, make sure to include the confidence level, the actual difference in the population proportions captured by the confidence interval (i.e. be specific to the context of the question), and express the limits as percents.
Steps to Conduct a Hypothesis Test for the Difference in Two Population Proportions
- Write down the null hypothesis that there is no difference in the population proportions:
[latex]\begin{eqnarray*}\\H_0:&&p_1-p_2=0\end{eqnarray*}[/latex]
The null hypothesis is always the claim that the two population proportions are equal ([latex]p_1=p_2[/latex]).
- Write down the alternative hypotheses in terms of the difference in the population proportions. The alternative hypothesis will be one of the following:
[latex]\begin{eqnarray*}H_a:p_1-p_2<0&&(p_1\lt p_2)\\H_a:p_1-p_2>0&&(p_1\gt p_2)\\H_a:p_1-p_2\neq 0&&(p_1\neq p_2)\\\\\end{eqnarray*}[/latex]
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- Check the conditions [latex]n_1\times\hat{p}_1\geq 5[/latex], [latex]n_1 \times (1-\hat{p}_1) \geq 5[/latex], [latex]n_2\times\hat{p}_2\geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex] to verify that the normal distribution applies. Use the normal distribution to find the p-value (the area in the corresponding tail) for the test. The [latex]z[/latex]-score is
[latex]\begin{eqnarray*}z=\frac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{\sqrt{\overline{p}\times(1-\overline{p})\times\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}&\;\;\;\;\;\;\;\;\;\;\;\;&\overline{p}=\frac{x_1+x_2}{n_1+n_2}\\\\\end{eqnarray*}[/latex]
- Compare the p-value to the significance level and state the outcome of the test:
- If p-value[latex]\leq\alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- If p-value[latex]\gt\alpha[/latex], do not reject [latex]H_0[/latex].
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- If p-value[latex]\leq\alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
- Write down a concluding sentence specific to the context of the question.
NOTES
- Because the population proportions [latex]p_1[/latex] and [latex]p_2[/latex] are often unknown, we replace the values of the population proportions with the sample proportions [latex]\hat{p}_1[/latex] and [latex]\hat{p}_2[/latex] in the normal distribution check. That is, when the population proportions are unknown, we check [latex]n_1\times\hat{p}_1\geq 5[/latex], [latex]n_1 \times (1-\hat{p}_1) \geq 5[/latex], [latex]n_2\times\hat{p}_2\geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex] to verify that the normal distribution applies to the calculation of the p-value.
- Because we are testing the equality of the two population proportions, the [latex]z[/latex]-score for the hypothesis test uses a pooled sample proportion [latex]\overline{p}[/latex]. The pooled sample proportion [latex]\overline{p}[/latex] combines the sample data to create an estimate of the overall proportion of success.
USING EXCEL TO CALCULE THE P-VALUE FOR A HYPOTHESIS TEST ON TWO INDEPENDENT POPULATION PROPORTIONS
The p-value for a hypothesis test on the difference in two population proportions is the area in the tail(s) of the normal distribution, assuming that the conditions for using a normal distribution are met ([latex]n_1\times p_1\geq 5[/latex], [latex]n_1\times(1-p_1)\geq 5[/latex], [latex]n_2 \times p_2 \geq 5[/latex] and [latex]n_2\times(1-p_2)\geq 5[/latex] ).
The p-value is the area in the tail(s) of a normal distribution, so the norm.dist(x,[latex]\mu[/latex],[latex]\sigma[/latex],logic operator) function can be used to calculate the p-value.
- For x, enter the value for [latex]\hat{p}_1-\hat{p}_2[/latex].
- For [latex]\mu[/latex], enter 0, the value of [latex]p_1-p_2[/latex] from the null hypothesis. This is the mean of the distribution of the differences in the sample proportions.
- For [latex]\sigma[/latex], enter the value of [latex]\displaystyle{\sqrt{\overline{p}\times(1-\overline{p})\times\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}[/latex] where [latex]\displaystyle{\overline{p}=\frac{x_1+x_2}{n_1+n_2}}[/latex]. The value for [latex]\sigma[/latex] is the bottom part of the [latex]z[/latex]-score used in the hypothesis test.
- For the logic operator, enter true. Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
As with the previous chapter, use the appropriate technique with the norm.dist function to find the area in the left-tail, the area in the right-tail or the sum of the area in tails.
EXAMPLE
A cell phone company claimed that iPhones are more popular with adults 30 years old or younger than with adults over 30 years old. A consumer advocacy group wants to test this claim. In a sample of 1340 adults 30 years old or younger, 134 own an iPhone. In a sample of 250 adults over the age of 30, 15 own an iPhone. At the 5% significance level, is the proportion of adults 30 years old or younger who own an iPhone greater than the proportion of adults over the age of 30 who own an iPhone?
Solution:
Let adults 30 years old or younger be population 1 and adults over 30 years old be population 2. From the question, we have the following information:
| 30 Years or Younger | Over 30 Years |
| [latex]n_1=1340[/latex] | [latex]n_2=250[/latex] |
| [latex]x_1=134[/latex] | [latex]x_2=15[/latex] |
| [latex]\hat{p}_1=\frac{134}{1340}=0.1[/latex] | [latex]\hat{p}_2=\frac{15}{250}=0.05[/latex] |
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p_1-p_2=0\\H_a:&&p_1-p_2\gt 0\end{eqnarray*}[/latex]
p-value:
Before calculating the p-value, we check that the normal distribution applies:
[latex]\begin{eqnarray*}n_1\times\hat{p}_1&=&1340\times 0.1=134\geq 5\\n_1\times(1-\hat{p}_1)&=&1340\times(1-0.1)=1206\geq 5\\n_2\times\hat{p}_2&=&250\times 0.05=15\geq 5\\n_2\times(1-\hat{p}_1)&=&250\times(1-0.05)=235\geq 5\end{eqnarray*}[/latex]
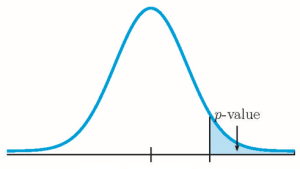
Because [latex]n_1 \times \hat{p}_1 \geq 5[/latex], [latex]n_1\times(1-\hat{p}_1)\geq 5[/latex], [latex]n_2 \times \hat{p}_2 \geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex], the normal distribution applies and so we use a normal distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\gt[/latex], the p-value is the area in the right tail of the distribution.
The pooled sample proportion is:
[latex]\begin{eqnarray*}\overline{p}&=&\frac{x_1+x_2}{n_1+n_2}\\&=&\frac{134+15}{1340+250}\\&=&\frac{149}{1590}\\&=&0.09371...\end{eqnarray*}[/latex]
| Function | 1-norm.dist | Answer |
| Field 1 | 0.1-0.05 | 0.0232 |
| Field 2 | 0 | |
| Field 3 | sqrt(0.09371… *(1-0.09371…)*(1/1340+1/250)) | |
| Field 4 | true |
So the p-value[latex]=0.0232[/latex].
Conclusion:
Because p-value[latex]=0.0232\lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that the proportion of adults 30 years old or younger who own an iPhone is greater than the proportion of adults over the age of 30 who own an iPhone.
NOTES
- The null hypothesis [latex]p_1-p_2=0[/latex] is the claim that the proportion of adults 30 or younger with an iPhone equals the proportion of adults over 30 with an iPhone. That is, the two populations have the same proportion.
- The alternative hypothesis [latex]p_1-p_2\gt 0[/latex] is the claim that the proportion of adults 30 or younger with an iPhone is greater than the proportion of adults over 30 with an iPhone ([latex]p_1\gt p_2[/latex]).
- Make sure to keep all of the decimal places throughout the calculation to avoid any round-off error in the p-value. Perform the calculations of the sample proportions and the pooled sample proportion [latex]\overline{p}[/latex] in Excel and then click on the corresponding cells when completing the fields in the norm.dist function.
- The p-value is the area in the right tail of the normal distribution. In the calculation of the p-value:
- The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
- Field 1 is the value of [latex]\hat{p}_1-\hat{p}_2=0.1-0.05[/latex].
- Field 2 is 0, the value of [latex]p_1-p_2[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p_1-p_2=0[/latex].
- Field 3 is the value of
[latex]\small\sqrt{\overline{p}\times(1-\overline{p})\times\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}=\sqrt{0.09371...\times(1-0.09371...)\times\left(\frac{1}{1340}+\frac{1}{250}\right)}[/latex]
- The p-value of 0.0232 is a small probability compared to the significance level, and so is unlikely to happen that assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of adults 30 years old or younger who own an iPhone is greater than the proportion of adults over the age of 30 who own an iPhone.
EXAMPLE
Two types of medication for hives are tested to determine if there is a difference in the proportions of adult patient reactions. In a sample of 200 adults given medication A, 20 still had hives 30 minutes after taking the medication. In a sample of 200 adults given medication B, 12 still had hives 30 minutes after taking the medication. At the 1% significance level, is there a difference in the proportion of adults who still have hives 30 minutes after taking medications?
Solution:
Let medication A be population 1 and medication B be population 2. From the question, we have the following information:
| Medication A | Medication B |
| [latex]n_1=200[/latex] | [latex]n_2=200[/latex] |
| [latex]x_1=20[/latex] | [latex]x_2=12[/latex] |
| [latex]\hat{p}_1=\frac{20}{200}=0.1[/latex] | [latex]\hat{p}_2=\frac{12}{200}=0.06[/latex] |
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p_1-p_2=0\\H_a:&&p_1-p_2\neq 0\end{eqnarray*}[/latex]
p-value:
Before calculating the p-value, we check that the normal distribution applies:
[latex]\begin{eqnarray*}n_1\times\hat{p}_1&=&200\times 0.1=20\geq 5\\n_1\times(1-\hat{p}_1)&=&200\times(1-0.1)=180\geq 5\\n_2\times\hat{p}_2&=&200\times 0.06=12\geq 5\\n_2\times(1-\hat{p}_1)&=&200\times(1-0.06)=188\geq 5\end{eqnarray*}[/latex]
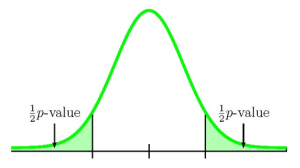
Because [latex]n_1 \times \hat{p}_1 \geq 5[/latex], [latex]n_1\times(1-\hat{p}_1)\geq 5[/latex], [latex]n_2 \times \hat{p}_2 \geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex], the normal distribution applies and so we use a normal distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\neq[/latex], the p-value is the sum of the area in the two tails of the distribution.
We need to know if the sample information relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution. In this case, [latex]\hat{p}_1\gt\hat{p}_2[/latex] ([latex]0.1\gt 0.06[/latex]), so the sample information relates to the right tail of the normal distribution. This means that we will calculate out the area in the right tail using 1-norm.dist. However, this is a two-tailed test where the p-value is the sum of the area in the two tails and the area in the right tail is only one half of the p-value. The area in the right tail equals the area in the left tail and the p-value is the sum of these two areas.
The pooled sample proportion is:
[latex]\begin{eqnarray*}\overline{p}&=&\frac{x_1+x_2}{n_1+n_2}\\&=&\frac{20+12}{200+200}\\&=&\frac{32}{400}\\&=&0.08\end{eqnarray*}[/latex]
| Function | 1-norm.dist | Answer |
| Field 1 | 0.1-0.06 | 0.0702 |
| Field 2 | 0 | |
| Field 3 | sqrt(0.08*(1-0.08)*(1/200+1/200)) | |
| Field 4 | true |
So the area in the right tail is 0.0702, which means [latex]\frac{1}{2}[/latex](p-value)[latex]=0.0702[/latex]. This is also the area in the left tail, so
p-value[latex]=0.0702+0.0702=0.1404[/latex]
Conclusion:
Because p-value[latex]=0.1404\gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the there is a difference in the proportion of adults who still have hives 30 minutes after taking medication.
NOTES
- The null hypothesis [latex]p_1-p_2=0[/latex] is the claim that the there is no difference in the proportion of adults with hives 30 minutes after taking the medications. That is, the two populations have the same proportion.
- The alternative hypothesis [latex]p_1-p_2\neq 0[/latex] is the claim that there is a difference in the proportion of adults with hives 30 minutes after taking the medications ([latex]p_1\neq p_2[/latex]).
- In a two-tailed hypothesis test that uses the normal distribution, we will only have sample information relating to one of the two tails. We must determine which of the tails the sample information belongs to, and then calculate out the area in that tail. The area in each tail represents exactly half of the p-value, so the p-value is the sum of the areas in the two tails.
- If the sample proportion [latex]\hat{p}_1[/latex] is less than the sample proportion [latex]\hat{p}_2[/latex] ([latex]\hat{p}_1\lt\hat{p}_2[/latex]), the sample information belongs to the left tail.
- We use norm.dist([latex]\hat{p}_1-\hat{p}_2[/latex],[latex]0[/latex],[latex]\sqrt{\overline{p}\times(1-\overline{p})\times\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}[/latex],true) to find the area in the left tail. The area in the right tail equals the area in the left tail, so we can find the p-value by adding the output from this function to itself.
- If the sample proportion [latex]\hat{p}_1[/latex] is greater than the sample proportion [latex]\hat{p}_2[/latex] ([latex]\hat{p}_1\gt\hat{p}_2[/latex]), the sample information belongs to the right tail.
- We use 1-norm.dist([latex]\hat{p}_1-\hat{p}_2[/latex],[latex]0[/latex],[latex]\sqrt{\overline{p}\times(1-\overline{p})\times\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}[/latex],true) to find the area in the right tail. The area in the left tail equals the area in the right tail, so we can find the p-value by adding the output from this function to itself.
- If the sample proportion [latex]\hat{p}_1[/latex] is less than the sample proportion [latex]\hat{p}_2[/latex] ([latex]\hat{p}_1\lt\hat{p}_2[/latex]), the sample information belongs to the left tail.
- The p-value of 0.1404 is a large probability compared to the significance level, and so is likely to happen assuming that the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, there is no difference in the proportion of adults with hives 30 minutes after taking the medications.
EXAMPLE
A valve manufacturer recently launched a new valve, Valve A, and they want to claim that the proportion of their valves that fail under 4500 psi is the smallest of all the other valves on the market. The manufacturer decides to compare Valve A with the most popular valve on the market, Valve B. In a sample of 100 Valve A’s, 6 failed at 4500 psi. In a sample of 150 Valve B’s, 16 failed at 4500 psi. At the 5% significance level, is the proportion of Valve As that fail under 4500 psi less than the proportion of Valve Bs that fail under 4500 psi?
Solution:
Let Valve A be population 1 and Valve B be population 2. From the question, we have the following information:
| Valve A | Valve B |
| [latex]n_1=100[/latex] | [latex]n_2=150[/latex] |
| [latex]x_1=6[/latex] | [latex]x_2=16[/latex] |
| [latex]\hat{p}_1=\frac{6}{100}=0.06[/latex] | [latex]\hat{p}_2=\frac{16}{150}=0.1066...[/latex] |
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p_1-p_2=0\\H_a:&&p_1-p_2\lt 0\end{eqnarray*}[/latex]
p-value:
Before calculating the p-value, we check that the normal distribution applies:
[latex]\begin{eqnarray*}n_1\times\hat{p}_1&=&100\times 0.06=6\geq 5\\n_1\times(1-\hat{p}_1)&=&100\times(1-0.06)=94\geq 5\\n_2\times\hat{p}_2&=&150\times 0.1066....=16\geq 5\\n_2\times(1-\hat{p}_1)&=&150\times(1-0.1066...)=134\geq 5\end{eqnarray*}[/latex]
Because [latex]n_1 \times \hat{p}_1 \geq 5[/latex], [latex]n_1\times(1-\hat{p}_1)\geq 5[/latex], [latex]n_2 \times \hat{p}_2 \geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex], the normal distribution applies and so we use a normal distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\lt[/latex], the p-value is the area in the left tail of the distribution.
The pooled sample proportion is:
[latex]\begin{eqnarray*}\overline{p}&=&\frac{x_1+x_2}{n_1+n_2}\\&=&\frac{6+16}{100+150}\\&=&\frac{22}{250}\\&=&0.088\end{eqnarray*}[/latex]
| Function | norm.dist | Answer |
| Field 1 | 0.06-0.1066… | 0.1010 |
| Field 2 | 0 | |
| Field 3 | [latex]sqrt(0.088*(1-0.088)*(1/100+1/150))[/latex] | |
| Field 4 | true |
So the p-value[latex]=0.1010[/latex].
Conclusion:
Because p-value[latex]=0.1010\gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that the proportion of Valve As that fail under 4500 psi less than the proportion of Valve Bs that fail under 4500 psi.
NOTES
- The null hypothesis [latex]p_1-p_2=0[/latex] is the claim that the proportion of valves that fail under 4500 psi is the same for both valves. That is, the two populations have the same proportion.
- The alternative hypothesis [latex]p_1-p_2\lt 0[/latex] is the claim that the proportion of Valve As that fail under 4500 psi less than the proportion of Valve Bs that fail under 4500 psi ([latex]p_1\lt p_2[/latex]).
- Make sure to keep all of the decimal places throughout the calculation to avoid any round-off error in the p-value. Perform the calculations of the sample proportions and the pooled sample proportion [latex]\overline{p}[/latex] in Excel and then click on the corresponding cells when completing the fields in the norm.dist function.
- The p-value of 0.1010 is a large probability compared to the significance level, and so is likely to happen assuming that the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the proportion of Valve As that fail under 4500 psi equals the proportion of Valve Bs that fail under 4500 psi. For the company, this means that they could not claim that the proportion of their valves that fail under 4500 psi is the smallest of all the other valves on the market.
Watch this video: Excel 2013 Statistical Analysis #71: Inference About Difference Between 2 Pop. Proportions Z Method by ExcelIsFun [28:03]
Concept Review
The general form of a confidence interval for the difference in two population proportions is
[latex]\begin{eqnarray*}\\\text{Lower Limit}&=&\hat{p}_1-\hat{p}_2-z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2\times(1-\hat{p}_2)}{n_2}}\\\\\text{Upper Limit}&=&\hat{p}_1-\hat{p}_2+z\times\sqrt{\frac{\hat{p}_1\times(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2\times(1-\hat{p}_2)}{n_2}}\\\end{eqnarray*}[/latex]
where [latex]z[/latex] is the positive [latex]z[/latex]-score of the standard normal distribution so the area under the normal distribution in between [latex]-z[/latex] and [latex]z[/latex] is [latex]C[/latex].
The hypothesis test for the difference in two population proportions with is a well established process:
- Write down the null and alternative hypotheses in terms of the differences in the population proportions [latex]p_1-p_2[/latex].
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- Check that [latex]n_1\times\hat{p}_1\geq 5[/latex], [latex]n_1 \times (1-\hat{p}_1) \geq 5[/latex], [latex]n_2\times\hat{p}_2\geq 5[/latex] and [latex]n_2\times(1-\hat{p}_2)\geq 5[/latex] to verify that the normal distribution applies.
- Find the p-value (the area in the corresponding tail) for the test using the normal distribution.
- Compare the p-value to the significance level and state the outcome of the test.
- Write down a concluding sentence specific to the context of the question.
Attribution
“10.3 Comparing Two Independent Population Proportions“ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.