7.2 Confidence Intervals for a Single Population Mean with Known Population Standard Deviation
LEARNING OBJECTIVES
- Calculate and interpret confidence intervals for estimating a population mean where the population standard deviation is known.
A confidence interval for a population mean with a known standard deviation is based on the fact that the sample means follow an approximately normal distribution. To construct a confidence interval for a single unknown population mean [latex]\mu[/latex], where the population standard deviation is known, we need [latex]\overline{x}[/latex], which is the point estimate of the unknown population mean [latex]\mu[/latex].
The confidence interval estimate will have the form:
[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & \overline{x}-\mbox{margin of error} \\ \\ \mbox{Upper Limit} & = & \overline{x}-\mbox{margin of error} \end{eqnarray*}[/latex]
The margin of error depends on the confidence level. The confidence level is often considered the probability that the calculated confidence interval estimate will contain the true population parameter. However, it is more accurate to state that the confidence level is the percent of confidence intervals that contain the true population parameter when repeated samples are taken. Most often, it is the choice of the person constructing the confidence interval to choose a confidence level of 90% or higher because that person wants to be reasonably certain of their conclusions.
Watch this video: Confidence Intervals – Introduction by Joshua Emmanual [3:34]
EXAMPLE
Suppose we have collected data from a sample. The sample mean is 7 and the margin of error is 2.5.
The confidence interval is:
[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & 7 -2.5=4.5 \\ \\ \mbox{Upper Limit} & = & 7+2.5 =9.5 \end{eqnarray*}[/latex]
If the confidence level is 95%, then we say that, “We estimate with 95% confidence that the true value of the population mean is between 4.5 and 9.5.”
TRY IT
Suppose we have data from a sample. The sample mean is 15 and the margin of error is 3.2. What is the confidence interval estimate for the population mean?
Click to see Solution
[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & 15 -3.2=11.8 \\ \\ \mbox{Upper LImit} & = & 15+3.2 =18.2 \end{eqnarray*}[/latex]
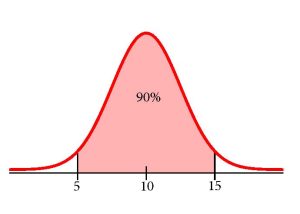
A confidence interval for a population mean with a known standard deviation is based on the fact that the sample means follow an approximately normal distribution. Suppose that our sample has a mean of [latex]\overline{x}=10[/latex] and we have constructed the 90% confidence interval with a lower limit of 5 and an upper limit of 15.
To get a 90% confidence interval, we must include the central 90% of the probability of the normal distribution. If we include the central 90%, we leave out a total of 10% in both tails, or 5% in each tail, of the normal distribution.
To capture the central 90%, we must go out 1.645 “standard deviations” on either side of the calculated sample mean. The value 1.645 is the [latex]z[/latex]-score from a standard normal probability distribution that puts an area of 0.90 in the center, an area of 0.05 in the far left tail, and an area of 0.05 in the far right tail.
It is important that the “standard deviation” used must be appropriate for the parameter we are estimating. So in this section we need to use the standard deviation that applies to sample means, which is [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex] (the standard deviation of the sample means). The fraction [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex] is commonly called the standard error of the mean in order to clearly distinguish the standard deviation for a sample mean from the population standard deviation [latex]\sigma[/latex].
Calculating the Confidence Interval
To construct a confidence interval estimate for an unknown population mean, we need data from a random sample. The steps to construct and interpret the confidence interval are:
- Calculate the sample mean [latex]\overline{x}[/latex] from the sample data. Remember, in this section we already know the population standard deviation [latex]\sigma[/latex].
- Find the [latex]z[/latex]-score that corresponds to the confidence level [latex]C[/latex].
- Calculate the limits for the confidence interval.
- Write a sentence that interprets the estimate in the context of the problem. (Explain what the confidence interval means, in the words of the problem.)
We will first examine each step in more detail, and then illustrate the process with some examples.
Finding the [latex]z[/latex]-score for the Confidence Level
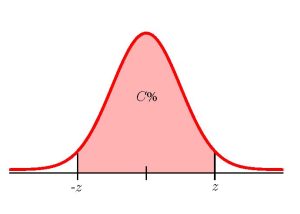
When we know the population standard deviation [latex]\sigma[/latex], we use a standard normal distribution to calculate the margin of error and construct the confidence interval. We need to find the value of [latex]z[/latex] that puts an area equal to the confidence level (in decimal form) in the middle of the standard normal distribution. The confidence level [latex]C[/latex] is the area in the middle of the standard normal distribution. The remaining area, [latex]1-C[/latex], is split equally between the two tails, so each of the tails contains an area equal to [latex]\displaystyle{\frac{1-C}{2}}[/latex].
The [latex]z[/latex]-score needed to construct the confidence interval is the [latex]z[/latex]-score so that the entire area to the left of [latex]z[/latex]-score equals the area in the middle (the confidence level) plus the area in the left tail [latex]\displaystyle{\left(\frac{1-C}{2}\right)}[/latex]. That is, the required [latex]z[/latex]-score for the confidence interval is the [latex]z[/latex]-score so that the entire area to the left of the [latex]z[/latex]-score is
[latex]\displaystyle{C+\frac{1-C}{2}}[/latex]
For example, if the confidence level is 95%, then the area in the center of the standard normal distribution is 0.95 and the area in the left tail is [latex]\displaystyle{\frac{1-0.95}{2}=0.025}[/latex]. We would need to find the [latex]z[/latex]-score so that the entire area to the left of the [latex]z[/latex]-score equals [latex]0.95+0.025=0.975[/latex].
CALCULATING THE [latex]\textcolor{white}z[/latex]-SCORE FOR A CONFIDENCE INTERVAL IN EXCEL
To find the [latex]z[/latex]-score to construct a confidence interval with confidence level [latex]C[/latex], use the norm.s.inv(area to the left of z) function.
- For area to the left of z, enter the entire area to the left of the [latex]z[/latex]-score you are trying to find. For a confidence interval, the area to the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
The output from the norm.s.inv function is the value of [latex]z[/latex]-score needed to construct the confidence interval.
NOTE
The norm.s.inv function requires that we enter the entire area to the left of the unknown [latex]z[/latex]-score. This area includes the confidence level (the area in the middle of the distribution) plus the remaining area in the left tail.
Calculating the Margin of Error
The margin of error for a confidence interval with confidence level [latex]C[/latex] for an unknown population mean [latex]\mu[/latex] when the population standard deviation [latex]\sigma[/latex] is known is
[latex]\displaystyle{\mbox{Margin of Error}=z \times \frac{\sigma}{\sqrt{n}}}[/latex]
where [latex]z[/latex] is the the [latex]z[/latex]-score so the area the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
Constructing the Confidence Interval
The limits for the confidence interval with confidence level [latex]C[/latex] for an unknown population mean [latex]\mu[/latex] when the population standard deviation [latex]\sigma[/latex] is known are
[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \end{eqnarray*}[/latex]
where [latex]z[/latex] is the [latex]z[/latex]-score so the area the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
Interpreting a Confidence Interval
The interpretation should clearly state the confidence level [latex]C[/latex], explain what population parameter is being estimated (in this case a population mean), and state the confidence interval (both endpoints)—”We estimate with ___% confidence that the true population mean (include the context of the problem) is between ___ and ___ (include appropriate units).”
Watch this video: Confidence Interval for a population mean – [latex]\sigma[/latex] known by Joshua Emmanuel [4:30]
EXAMPLE
Suppose scores on exams in statistics are normally distributed with an unknown population mean and a population standard deviation of 3 points. A random sample of 36 scores is taken and has a sample mean of 68 points.
- Find a 90% confidence interval for the mean exam score.
- Interpret the confidence interval found in part 1.
- Is it reasonable to conclude that the mean exam score for all the exams is 70? Explain.
Solution:
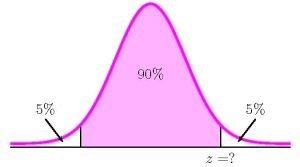
- To find the confidence interval, we need to find the [latex]z[/latex]-score for the 90% confidence interval. This means that we need to find the [latex]z[/latex]-score so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.9+\frac{1-0.9}{2}=0.95}[/latex].
Function norm.s.inv Answer Field 1 0.95 1.6448… So [latex]z=1.6448....[/latex]. From the question [latex]\overline{x}=68[/latex], [latex]\sigma=3[/latex] and [latex]n=36[/latex]. The 90% confidence interval is
[latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68-1.6448... \times \frac{3}{\sqrt{36}} \\ & = & 67.18 \\ \\\mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68+1.6448... \times \frac{3}{\sqrt{36}} \\ & = & 68.82 \\ \\ \end{eqnarray*}[/latex]
- We are 90% confident that the mean exam score is between 67.18 points and 68.82 points.
- It is not reasonable to conclude that the mean exam score is 70 points because 70 points is outside the confidence interval. (In this case there is a 90% chance that the actual mean exam score is in between 67.18 and 68.82 and only a 10% chance that the mean exam score is outside this interval. So it is unlikely (but not impossible) that the actual mean exam score is a value outside of the confidence interval.)
NOTES
- When calculating the limits for the confidence interval keep all of the decimals in the [latex]z[/latex]-score and other values throughout the calculation. This will ensure that there is no round-off error in the answers. You can use Excel to do the calculation of the limits, clicking on the cells containing the [latex]z[/latex]-score and any other values, to ensure that all of the decimal places are used in the calculation.
- When writing down the interpretation of the confidence interval, make sure to include the confidence level, the actual population mean captured by the confidence interval (i.e. be specific to the context of the question), and appropriate units for the limits.
- 90% of all confidence interval constructed this way contain the true mean exam score. For example, if we constructed 100 of these confidence intervals (using 100 different samples of size 36), we would expect 90 of them to contain the true mean exam score.
TRY IT
Suppose average pizza delivery times are normally distributed with an unknown population mean and a population standard deviation of 6 minutes. A random sample of 28 pizza delivery restaurants is taken and has a sample mean delivery time of 36 minutes.
- Find a 96% confidence interval for the mean delivery time.
- Interpret the confidence interval found in part 1.
- Is it reasonable to claim that the mean delivery time is 35 minutes? Explain.
Click to see Solution
-
Function norm.s.inv Answer Field 1 0.98 2.053…  [latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 36-2.053... \times \frac{6}{\sqrt{28}} \\ & = & 33.67 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 36+2.053... \times \frac{6}{\sqrt{28}} \\ & = & 38.05 \\ \\ \end{eqnarray*}[/latex]
[latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 36-2.053... \times \frac{6}{\sqrt{28}} \\ & = & 33.67 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 36+2.053... \times \frac{6}{\sqrt{28}} \\ & = & 38.05 \\ \\ \end{eqnarray*}[/latex] - We are 96% confident that the mean delivery time is between 33.67 minutes and 38.05 minutes.
- It is reasonable to conclude that the mean delivery time is 35 minutes because 35 minutes is inside the confidence interval.
EXAMPLE
The Specific Absorption Rate (SAR) for a cell phone measures the amount of radio frequency (RF) energy absorbed by the user’s body when using the handset. Every cell phone emits RF energy. Different phone models have different SAR measures. To receive certification from the Federal Communications Commission (FCC) for sale in the United States, the SAR level for a cell phone must be no more than 1.6 watts per kilogram. This table shows the highest SAR level for a random selection of cell phone models as measured by the FCC.
| Phone Model | SAR | Phone Model | SAR | Phone Model | SAR |
|---|---|---|---|---|---|
| Apple iPhone 4S | 1.11 | LG Ally | 1.36 | Pantech Laser | 0.74 |
| BlackBerry Pearl 8120 | 1.48 | LG AX275 | 1.34 | Samsung Character | 0.5 |
| BlackBerry Tour 9630 | 1.43 | LG Cosmos | 1.18 | Samsung Epic 4G Touch | 0.4 |
| Cricket TXTM8 | 1.3 | LG CU515 | 1.3 | Samsung M240 | 0.867 |
| HP/Palm Centro | 1.09 | LG Trax CU575 | 1.26 | Samsung Messager III SCH-R750 | 0.68 |
| HTC One V | 0.455 | Motorola Q9h | 1.29 | Samsung Nexus S | 0.51 |
| HTC Touch Pro 2 | 1.41 | Motorola Razr2 V8 | 0.36 | Samsung SGH-A227 | 1.13 |
| Huawei M835 Ideos | 0.82 | Motorola Razr2 V9 | 0.52 | SGH-a107 GoPhone | 0.3 |
| Kyocera DuraPlus | 0.78 | Motorola V195s | 1.6 | Sony W350a | 1.48 |
| Kyocera K127 Marbl | 1.25 | Nokia 1680 | 1.39 | T-Mobile Concord | 1.38 |
- Find a 98% confidence interval for the mean of the Specific Absorption Rates (SARs) for cell phones. Assume that the population standard deviation is [latex]\sigma = 0.337[/latex].
- Interpret the confidence interval found in part 1.
Solution:
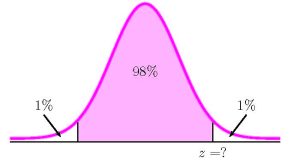
- To find the confidence interval, we need to find the [latex]z[/latex]-score for the 98% confidence interval. This means that we need to find the [latex]z[/latex]-score so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.98+\frac{1-0.98}{2}=0.99}[/latex].
Function norm.s.inv Answer Field 1 0.99 2.3263… So [latex]z=2.3263....[/latex]. From the sample data supplied in the question [latex]\overline{x}=1.0237...[/latex] and [latex]n=30[/latex]. The population standard deviation is [latex]\sigma=0.337[/latex]. The 98% confidence interval is
[latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 1.0237...-2.3263... \times \frac{0.377}{\sqrt{30}} \\ & = & 0.8806 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 1.0237...+2.3262... \times \frac{0.377}{\sqrt{30}} \\ & = & 1.1839 \\ \\ \end{eqnarray*}[/latex]
- We are 98% confident that the mean of the Specific Absorption Rates is between 0.8806 watts per kilogram and 1.1839 watts per kilogram.
TRY IT
This table shows a different random sampling of 20 cell phone models. As previously, assume that the population standard deviation is [latex]\sigma = 0.337[/latex].
| Phone Model | SAR | Phone Model | SAR |
|---|---|---|---|
| Blackberry Pearl 8120 | 1.48 | Nokia E71x | 1.53 |
| HTC Evo Design 4G | 0.8 | Nokia N75 | 0.68 |
| HTC Freestyle | 1.15 | Nokia N79 | 1.4 |
| LG Ally | 1.36 | Sagem Puma | 1.24 |
| LG Fathom | 0.77 | Samsung Fascinate | 0.57 |
| LG Optimus Vu | 0.462 | Samsung Infuse 4G | 0.2 |
| Motorola Cliq XT | 1.36 | Samsung Nexus S | 0.51 |
| Motorola Droid Pro | 1.39 | Samsung Replenish | 0.3 |
| Motorola Droid Razr M | 1.3 | Sony W518a Walkman | 0.73 |
| Nokia 7705 Twist | 0.7 | ZTE C79 | 0.869 |
- Construct a 93% confidence interval for the mean SAR for cell phones certified for use in the United States.
- Interpret the confidence interval found in part 1.
Click to see Solution
-
Function norm.s.inv Answer Field 1 0.965 1.8119… [latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 0.94...-1.8119... \times \frac{0.337}{\sqrt{20}} \\ & = & 0.8035 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 0.94...+1.8119... \times \frac{0.337}{\sqrt{20}} \\ & = & 1.0766 \\ \\ \end{eqnarray*}[/latex]
- We are 93% confident that the mean of the Specific Absorption Rates is between 0.8035 watts per kilogram and 1.0766 watts per kilogram.
Notice the difference in the confidence intervals calculated in the Example and Try It just completed. These intervals are different for several reasons: they were calculated from different samples, the samples were different sizes, and the intervals were calculated for different levels of confidence. Even though the intervals are different, they do not yield conflicting information.
Changing the Confidence Level
EXAMPLE
Suppose scores on exams in statistics are normally distributed with an unknown population mean and a population standard deviation of 3 points. A random sample of 36 scores is taken and gives a sample mean of 68 points. Previously we found a 90% confidence interval for the mean exam score. Now, find a 95% confidence interval for the mean exam score. Interpret the 95% confidence interval.
Solution:
To find the confidence interval, we need to find the [latex]z[/latex]-score for the 95% confidence interval. This means that we need to find the [latex]z[/latex]-score so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.95+\frac{1-0.95}{2}=0.975}[/latex].
| Function | norm.s.inv | Answer |
| Field 1 | 0.975 | 1.9599… |
So [latex]z=1.9599....[/latex]. From the question [latex]\overline{x}=68[/latex], [latex]\sigma=3[/latex] and [latex]n=36[/latex]. The 95% confidence interval is
[latex]\begin{eqnarray*}\\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68-1.9599... \times \frac{3}{\sqrt{36}} \\ & = & 67.02 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68+1.9599... \times \frac{3}{\sqrt{36}} \\ & = & 68.98 \\ \\ \end{eqnarray*}[/latex]
We are 95% confident that the mean exam score is between 67.02 points and 68.98 points.
Comparing the Results
For the exam scores examples, the 90% confidence interval has a lower limit of 67.18 and an upper limit of 68.82, and the 95% confidence interval has a lower limit of 67.02 and an upper limit of 68.98. Notice that the 95% confidence interval is wider (the distance between the limits is larger in the 95% confidence interval). If we look at the graphs, because the area 0.95 is larger than the area 0.90, it makes sense that the 95% confidence interval is wider. To be more confident that the confidence interval actually does contain the true value of the population mean for all statistics exam scores, the confidence interval necessarily needs to be wider.
Effect of Changing the Confidence Level
- Increasing the confidence level increases the margin of error, making the confidence interval wider.
- Decreasing the confidence level decreases the margin of error, making the confidence interval narrower.
Changing the Sample Size
EXAMPLE
Suppose scores on exams in statistics are normally distributed with an unknown population mean and a population standard deviation of 3 points. Previously, we found a 90% confidence interval for the mean exam score using a sample of size 36 with a sample mean of 68.
- Suppose everything is kept the same but the sample size is 100 (instead of 36). Find the 90% confidence interval.
- Suppose everything is kept the same but the sample size is 25 (instead of 36). Find the 90% confidence interval.
Solution:
-
Function norm.s.inv 1.6448… Field 1 0.95 [latex]\begin{eqnarray*}\\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68-1.6448... \times \frac{3}{\sqrt{100}} \\ & = & 67.51 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68+1.6448... \times \frac{3}{\sqrt{100}} \\& = & 68.49 \\ \\ \end{eqnarray*}[/latex]
-
Function norm.s.inv 1.6448… Field 1 0.95 [latex]\begin{eqnarray*}\\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68-1.6448... \times \frac{3}{\sqrt{25}} \\ & = & 67.01 \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}} \\ & = & 68+1.6448... \times \frac{3}{\sqrt{25}} \\& = & 69.27\end{eqnarray*}[/latex]
Comparing the Results
For the exam scores examples, the 90% confidence interval with a sample size of 36 has a lower limit of 67.18 and an upper limit of 68.82, with a sample size of 100 has a lower limit is 67.51 and an upper limit is 68.49, and with a sample size of 25 has a lower limit is 67.01 and an upper limit is 69.27. When the sample size increased, the confidence interval is narrower. When the sample size decreased, the confidence interval is wider. Generally, the smaller the sample size, the wider the confidence interval needs to be in order to achieve the same level of confidence.
Effect of Changing the Sample Size
- Increasing the sample size causes the margin of error to decrease, making the confidence interval narrower.
- Decreasing the sample size causes the margin of error to increase, making the confidence interval wider.
Concept Review
In this section, we learned how to calculate the confidence interval for a single population mean where the population standard deviation is known. A confidence interval has the general form:
[latex]\begin{eqnarray*}\\ \mbox{Lower Limit} & = & \overline{x}-\mbox{margin of error} \\ \\ \mbox{Upper Limit} & = & \overline{x}-\mbox{margin of error}\\ \\ \end{eqnarray*}[/latex]
The general form for a confidence interval for a single population mean, known standard deviation is given by
[latex]\begin{eqnarray*}\\ \mbox{Lower Limit} & = & \overline{x}-z \times \frac{\sigma}{\sqrt{n}} \\ \\ \mbox{Upper Limit} & = & \overline{x}+z \times \frac{\sigma}{\sqrt{n}}\\ \\ \end{eqnarray*}[/latex]
where [latex]z[/latex] is the the [latex]z[/latex]-score so the area the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
The calculation of the margin of error depends on the size of the sample and the level of confidence required. The confidence level is the percent of all possible samples that can be expected to include the true population parameter. As the confidence level increases, the corresponding margin of error increases as well. As the sample size increases, the margin of error decreases.
Attribution
“8.1 A Single Population Mean using the Normal Distribution“ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.