9.4 Statistical Inference for Matched Samples
LEARNING OBJECTIVES
- Construct and interpret a confidence interval for the mean difference for matched samples.
- Conduct and interpret hypothesis tests for matched samples.
The comparison of two population means is very common. Often, we want to find out if the two populations under study have the same mean or if there is some difference in the two population means. The approach we take when studying two population means depends on whether the samples are independent or matched.
In a matched sample experiment, there is some relationship between pairs of data in the samples. Inferences on matched samples are typically more accurate than inferences on independent samples because matched samples reduce the variability measures to only the ones within the pairs.
EXAMPLE
In a clinical trial for a new drug, patients are tested before the drug is administered and then the same group of patients are tested after being given the drug. This is a matched sample experiment because the same group of patients is measured before and after the administration of the drug. In this way, there are a pair of observations (a before measurement and an after measurement) for each patient.
EXAMPLE
A manufacturing company wants to know which of two different production methods allow employees to perform a task the fastest. The table below illustrates the difference in an independent sample design and a matched sample design to test the difference in the average time it takes to perform the task using the two different methods.
| Independent Sample Design | Matched Sample Design |
|
|
In the independent sample design, there is no relationship between the two groups of employees. In the matched sample design, there is one group of employees with a pair of observations (a time from Method 1 and a time from Method 2) for each employee.
In matched sample designs, we work with the differences in the paired observations. We combine the two samples into a single sample by calculating out the difference between each of the paired observations. Throughout this section, we will use the following notation for the sample size, mean, and standard deviation of the differences in the paired observations:
| Symbol for: | Symbol |
| Population Mean of the Differences in the Paired Data | [latex]\mu_D[/latex] |
| Population Standard Deviation of the Differences in the Paired Data | [latex]\sigma_D[/latex] |
| Sample Size of the Differences in the Paired Data | [latex]n_D[/latex] |
| Sample Mean of the Differences in the Paired Data | [latex]\overline{x}_D[/latex] |
| Sample Standard Deviation of the Differences in the Paired Data | [latex]s_D[/latex] |
In order to construct a confidence interval or conduct a hypothesis test on the mean of the differences in the paired data ([latex]\mu_D[/latex]), we need to use the distribution of the differences in the paired data. In such cases, we need the distribution of the differences in the paired data to be normal, either because the differences are assumed to be normal or because the sample size [latex]n_D[/latex] is large enough ([latex]n_D \geq 30[/latex]).
By calculating out the differences in the paired data, we combine the two samples into a single sample consisting of the differences in the paired data. We use the differences to construct the confidence interval and run the hypothesis test. The confidence interval on the mean difference [latex]\mu_D[/latex] is a confidence interval for a single population mean. Similarly, the hypothesis test on the mean difference [latex]\mu_D[/latex] is actually a hypothesis test on a single population mean. In this case, we will follow the exact same procedures as we learned previously for a single population mean confidence interval and hypothesis test, only now the single population consists of the differences in the paired data.
When working with a matched sample design and the differences in the paired data, the population standard deviation will be unknown. So we will need to estimate the population standard deviation with the sample standard deviation. As we have seen previously, this means we must use a [latex]t[/latex]-distribution in the confidence intervals and hypothesis test on the mean of the differences in the paired data.
Constructing a Confidence Interval for the Difference in Two Population Means with Matched Samples
Suppose matched samples, each of size [latex]n[/latex], are taken from two related populations. The sample mean [latex]\overline{x}_D[/latex] and sample standard deviation [latex]s_D[/latex] for the differences in the matched pairs are calculated. The limits for the confidence interval with confidence level [latex]C[/latex] for the mean difference [latex]\displaystyle{\mu_D}[/latex] are:
[latex]\begin{eqnarray*}\\\text{LowerLimit}&=&\overline{x}_D-t\times\frac{s_D}{\sqrt{n_D}}\\\\\text{UpperLimit}&=&\overline{x}_D+t\times\frac{s_D}{\sqrt{n_D}}\\\\\end{eqnarray*}[/latex]
where [latex]t[/latex] is the positive [latex]t[/latex]-score of the [latex]t[/latex]-distribution with [latex]\displaystyle{df=n_D-1}[/latex] so that the area under the curve in between [latex]-t[/latex] and [latex]t[/latex] is [latex]C\%[/latex].
NOTES
- In order to construct the confidence interval for the mean difference, we need to check that the distribution of the differences in the paired data follows a normal distribution. This means that we need to check that either the differences follow a normal distribution or that the sample size is large enough (greater than or equal to 30).
- When the population standard deviations are unknown, we must use a [latex]t[/latex]-distribution in the construction of the confidence interval.
CALCULATING THE [latex]{\color{white}{t}}[/latex]-SCORE FOR A CONFIDENCE INTERVAL IN EXCEL
To find the [latex]t[/latex]-score to construct a confidence interval with confidence level [latex]C[/latex], use the t.inv.2t(area in the tails, degrees of freedom) function.
- For area in the tails, enter the sum of the area in the tails of the [latex]t[/latex]-distribution. For a confidence interval, the area in the tails is [latex]1-C[/latex].
- For degrees of freedom, enter the degrees of freedom [latex]\displaystyle{df = n_D-1}[/latex].
The output from the t.inv.2t function is the value of the [latex]t[/latex]-score needed to construct the confidence interval.
NOTE
The t.inv.2t function requires that we enter the sum of the area in both tails. The area in the middle of the distribution is the confidence level [latex]C[/latex], so the sum of the area in both tails is the leftover area [latex]1-C[/latex].
EXAMPLE
A company has two different methods that employees can use to complete a manufacturing task. A sample of workers is taken and the time, in minutes, that each worker takes to complete the task using each method is recorded. The data is shown in the table below. Assume the differences in the paired times have a normal distribution.
| Worker | Method 1 | Method 2 |
| 1 | 5.5 | 6.8 |
| 2 | 6.9 | 6.6 |
| 3 | 6.1 | 5.1 |
| 4 | 6 | 6.8 |
| 5 | 7 | 6.7 |
| 6 | 6.7 | 6.5 |
| 7 | 6.4 | 5.8 |
| 8 | 7 | 6.8 |
| 9 | 6.6 | 5.3 |
| 10 | 5.7 | 5.8 |
| 11 | 5.9 | 6.9 |
| 12 | 7 | 6.7 |
| 13 | 5.4 | 6.5 |
| 14 | 5.4 | 6.3 |
| 15 | 5.3 | 5 |
- Construct a 98% confidence interval for the mean difference in the time it takes the workers to complete the task.
- Interpret the confidence interval found in part 1.
- Is there evidence to suggest that the mean completion time for the two methods is the same? Explain.
Solution:
- We start by calculating out the differences in the paired data. We will calculate the differences as Method 1-Method 2.
Worker Method 1 Method 2 Difference 1 5.5 6.8 -1.3 2 6.9 6.6 0.3 3 6.1 5.1 1 4 6 6.8 -0.8 5 7 6.7 0.3 6 6.7 6.5 0.2 7 6.4 5.8 0.6 8 7 6.8 0.2 9 6.6 5.3 1.3 10 5.7 5.8 -0.1 11 5.9 6.9 -1 12 7 6.7 0.3 13 5.4 6.5 -1.1 14 5.4 6.3 -0.9 15 5.3 5 0.3 From the difference column, we have [latex]n_D=15[/latex], [latex]\overline{x}_D=-0.0466...[/latex], and [latex]s_D=0.7936...[/latex].
To find the confidence interval, we need to find the [latex]t[/latex]-score for the 98% confidence interval. This means that we need to find the [latex]t[/latex]-score so that the sum of the area in the tails is [latex]1-0.98=0.02[/latex]. The degrees of freedom for the [latex]t[/latex]-distribution is [latex]df=n_D-1=15-1=14[/latex].
Function t.inv.2t Answer Field 1 0.02 2.6244... Field 2 14 So [latex]t=2.6244...[/latex]. The 98% confidence interval is
[latex]\begin{eqnarray*}\\\text{Lower Limit}&=&\overline{x}_D-t\times\frac{s_D}{\sqrt{n_D}}\\&=&-0.0466...-2.6244...\times\frac{0.7936...}{\sqrt{15}}\\&=&-0.584\\\\\text{Upper Limit}&=&\overline{x}_D+t\times\frac{s_D}{\sqrt{n_D}}\\&=&-0.0466...+2.6244...\times\frac{0.7936...}{\sqrt{15}}\\&=&0.491\\\\\end{eqnarray*}[/latex]
- We are 98% confident that the mean difference in the completion times using the two methods is between -0.584 minutes and 0.491 minutes.
- Because 0 is inside the confidence interval, it suggests that the mean difference [latex]\displaystyle{\mu_D}[/latex] is 0. That is, [latex]\displaystyle{\mu_D= 0}[/latex]. This suggests that the mean completion times for the two methods are the same.
NOTES
- When calculating the limits for the confidence interval keep all of the decimals in the [latex]t[/latex]-score and other values throughout the calculation. This will ensure that there is no round-off error in the answers. You can use Excel to do the calculation of the differences, sample mean, sample standard deviation, and the limits, clicking on the corresponding cells to ensure that all of the decimal places are used in the calculation.
- When writing down the interpretation of the confidence interval, make sure to include the confidence level, the actual mean difference captured by the confidence interval (i.e. be specific to the context of the question), and appropriate units for the limits.
Steps to Conduct a Hypothesis Test for the Difference in Two Population Means with Matched Samples
- Write down the null hypothesis that the mean difference is 0:
[latex]\begin{eqnarray*}\\H_0:&&\mu_D=0\end{eqnarray*}[/latex]
The null hypothesis is always the claim that there is no difference in the two population means.
- Write down the alternative hypotheses in terms of the mean difference. The alternative hypothesis will be one of the following:
[latex]\begin{eqnarray*}H_a:&&\mu_D\leq 0\\H_a:&&\mu_D>0\\H_a:&&\mu_D\neq 0\\\\\end{eqnarray*}[/latex]
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- Use a [latex]t[/latex]-distribution to find the p-value (the area in the corresponding tail) for the test. The [latex]t[/latex]-score and degrees of freedom are
[latex]\begin{eqnarray*}t=\frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n_D}}}&\;\;\;\;\;\;\;\;\;\;\;&df=n_D-1\end{eqnarray*}[/latex]
- Compare the p-value to the significance level and state the outcome of the test:
- If p-value[latex]\leq \alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- If p-value[latex]\gt \alpha[/latex], do not reject [latex]H_0[/latex].
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- If p-value[latex]\leq \alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
USING EXCEL TO CALCULE THE P-VALUE FOR A HYPOTHESIS TEST ON MATCHED SAMPLES
The p-value for a hypothesis test on the mean difference in matched samples is the area in the tail(s) of the [latex]t[/latex]-distribution.
If the p-value is the area in the left tail:
- Use the t.dist function to find the p-value. In the t.dist(t-score, degrees of freedom, logic operator) function:
- For t-score, enter the value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n_D}}}}[/latex].
- For degrees of freedom, enter the degrees of freedom calculated using [latex]\displaystyle{df =n_D-1}[/latex].
- For the logic operator, enter true. Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
If the p-value is the area in the right tail:
- Use the t.dist.rt function to find the p-value. In the t.dist.rt(t-score, degrees of freedom) function:
- For t-score, enter the value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n_D}}}}[/latex].
- For degrees of freedom, enter the degrees of freedom calculated using [latex]\displaystyle{df =n_D-1}[/latex].
If the p-value is the sum of the area in the two tails:
- Use the t.dist.2t function to find the p-value. In the t.dist.2t(t-score, degrees of freedom) function:
- For t-score, enter the absolute value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n_D}}}}[/latex]. Note: In the t.dist.2t function, the value of the [latex]t[/latex]-score must be a positive number. If the [latex]t[/latex]-score is negative, enter the absolute value of the [latex]t[/latex]-score into the t.dist.2t function.
- For degrees of freedom, enter the degrees of freedom calculated using [latex]\displaystyle{df =n_D-1}[/latex].
EXAMPLE
A study was conducted to investigate the effectiveness of hypnosis on reducing pain. Eight subjects are randomly selected. Each subject's pain is measured before and after being hypnotized. A lower score indicates less pain. Assume the differences in the before and after scores have a normal distribution. At the 5% significance level, are the pain sensory measurements, on average, lower after hypnotism?
| Subject: | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Before | 6.6 | 6.5 | 9.0 | 10.3 | 11.3 | 8.1 | 6.3 | 11.6 |
| After | 6.8 | 2.4 | 7.4 | 8.5 | 8.1 | 6.1 | 3.4 | 2.0 |
Solution:
We start by calculating out the differences in the paired data. We will calculate the differences as before-after.
| Subject | Before | After | Difference |
| A | 6.6 | 6.8 | -0.2 |
| B | 6.5 | 2.4 | 4.1 |
| C | 9 | 7.4 | 1.6 |
| D | 10.3 | 8.5 | 1.8 |
| E | 11.3 | 8.1 | 3.2 |
| F | 8.1 | 6.1 | 2 |
| G | 6.3 | 3.4 | 2.9 |
| H | 11.6 | 2 | 9.6 |
From the difference column, we have [latex]n_D=8[/latex], [latex]\overline{x}_D=3.125[/latex], and [latex]s_D=2.911...[/latex].
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&\mu_D=0\\H_a:&&\mu_D\gt 0\end{eqnarray*}[/latex]
p-value:
This is a test on the mean difference in matched samples, so we use a [latex]t[/latex]-distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\gt[/latex], the p-value is the area in the right tail of the distribution.
To use the t.dist.rt function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n}_D}} \\ & = & \frac{3.125-0}{\frac{2.911...}{\sqrt{8}}} \\ & = & 3.0359... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n_D-1=8-1=7[/latex].
| Function | t.dist.rt | Answer |
| Field 1 | 3.0359.... | 0.0095 |
| Field 2 | 7 |
So the p-value[latex]=0.0095[/latex].
Conclusion:
Because p-value[latex]=0.0095 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that, on average, the pain sensory measurements are lower after hypnotism.
NOTES
- Before writing down the hypotheses, decide on the order of subtraction for calculating the differences. In a matched sample experiment, the form of the alternative hypothesis depends on the order of subtraction, so we must decide on the order of subtraction before writing down the hypotheses.
- The null hypothesis [latex]\mu_D=0[/latex] is the claim that there is no difference in the pain sensory measurements after hypnosis. That is, the average pain sensory measurement is the same before and after hypnosis.
- For the alternative hypothesis, we are testing that the after score is lower than the before score. In other words, before>after. Because we calculated the differences as before-after, before>after means before-after>0. So the alternative hypothesis is [latex]\mu_D \gt 0[/latex], the claim that the before score is larger than the after score (or the after score is lower than the before score).
- Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p-value. This ensures that we get the most accurate value for the p-value. Use Excel to do the calculations, and then click on the cells in subsequent calculations.
- The p-value of 0.0095 is a small probability compared to the significance level, and so is unlikely to happen assuming that the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the after score is, on average, lower than the before score.
EXAMPLE
A study was conducted to investigate how effective a new diet was in lowering cholesterol. Nine patients were selected for the new diet and their cholesterol was measured before and after starting the new diet. The results are recorded in the table below. Assume the differences have a normal distribution. At the 5% significance level, was the new diet, on average, successful in lowering patients' cholesterol?
| Subject | A | B | C | D | E | F | G | H | I |
| Before | 209 | 210 | 205 | 198 | 216 | 217 | 238 | 240 | 222 |
| After | 199 | 207 | 189 | 209 | 217 | 202 | 211 | 223 | 201 |
Solution:
We start by calculating out the differences in the paired data. We will calculate the differences as after-before.
| Subject | Before | After | Difference |
| A | 209 | 199 | -10 |
| B | 210 | 207 | -3 |
| C | 205 | 189 | -16 |
| D | 198 | 209 | 11 |
| E | 216 | 217 | 1 |
| F | 217 | 202 | -15 |
| G | 238 | 211 | -27 |
| H | 240 | 223 | -17 |
| I | 222 | 201 | -21 |
From the difference column, we have [latex]n_D=9[/latex], [latex]\overline{x}_D=-10.777...[/latex], and [latex]s_D=11.861...[/latex].
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&\mu_D=0\\H_a:&&\mu_D\lt 0\end{eqnarray*}[/latex]
p-value:
This is a test on the mean difference in matched samples, so we use a [latex]t[/latex]-distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\lt[/latex], the p-value is the area in the left tail of the distribution.
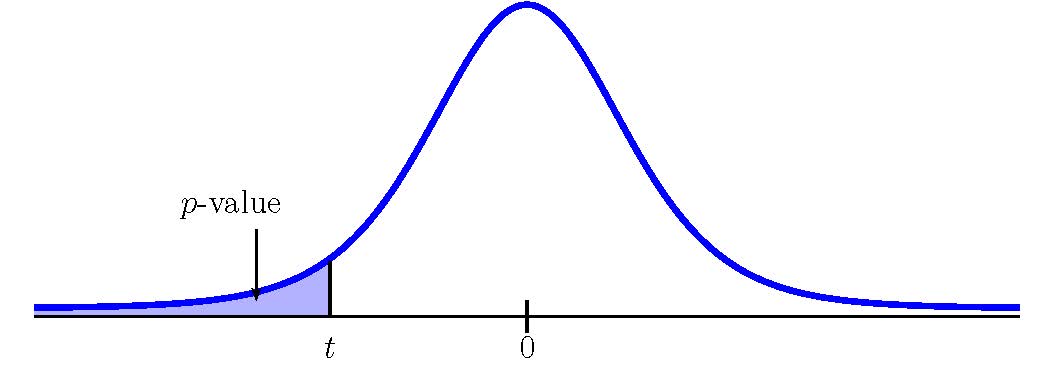 To use the t.dist function, we need to calculate out the [latex]t[/latex]-score:
To use the t.dist function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n}_D}} \\ & = & \frac{-10.777...-0}{\frac{11.861...}{\sqrt{9}}} \\ & = & -2.725... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n_D-1=9-1=8[/latex].
| Function | t.dist | Answer |
| Field 1 | -2.725... | 0.0130 |
| Field 2 | 8 | |
| Field 3 | true |
So the p-value[latex]=0.0130[/latex].
Conclusion:
Because p-value[latex]=0.0130 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that, on average, the new diet lowered the patients' cholesterol levels.
NOTES
- Before writing down the hypotheses, decide on the order of subtraction for calculating the differences. In a matched sample experiment, the form of the alternative hypothesis depends on the order of subtraction, so we must decide on the order of subtraction before writing down the hypotheses.
- The null hypothesis [latex]\mu_D=0[/latex] is the claim that there is no difference in the patients' cholesterol level. That is, the average cholesterol level is the same before and after the diet.
- For the alternative hypothesis, we are testing that the after score is lower than the before score. In other words, after<before. Because we calculated the differences as after-before, after<before means after-before<0. So, the alternative hypothesis is [latex]\mu_D \lt 0[/latex], the claim that the after score is lower than the before score.
- Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p-value. This ensures that we get the most accurate value for the p-value. Use Excel to do the calculations, and then click on the cells in subsequent calculations.
- The p-value of 0.0224 is a small probability compared to the significance level, and so is unlikely to happen assuming that the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the after score is, on average, lower than the before score.
EXAMPLE
Seven eighth graders at Kennedy Middle School measured how far they could push the shot-put with their dominant (writing) hand and their weaker (non-writing) hand. They thought that they could push equal distances with either hand. The results from their throws are recorded in the table below. Assume the differences are normally distributed. At the 5% significance level, is there a difference in the average distance for the dominant versus weaker hand?
| Distance (in feet) | Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student 7 |
|---|---|---|---|---|---|---|---|
| Dominant Hand | 30 | 26 | 34 | 17 | 19 | 26 | 20 |
| Weaker Hand | 28 | 14 | 27 | 18 | 17 | 26 | 16 |
Solution:
We start by calculating out the differences in the paired data. We will calculate the differences as dominant-weaker.
| Student | Dominant | Weaker | Difference |
| 1 | 30 | 28 | 2 |
| 2 | 26 | 14 | 12 |
| 3 | 34 | 27 | 7 |
| 4 | 17 | 18 | -1 |
| 5 | 19 | 17 | 2 |
| 6 | 26 | 26 | 0 |
| 7 | 20 | 16 | 4 |
From the difference column, we have [latex]n_D=7[/latex], [latex]\overline{x}_D=3.714...[/latex], and [latex]s_D=4.498...[/latex].
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&\mu_D=0\\H_a:&&\mu_D\neq 0\end{eqnarray*}[/latex]
p-value:
This is a test on the mean difference in matched samples, so we use a [latex]t[/latex]-distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\neq[/latex], the p-value is the sum of area in the tails of the distribution.
To use the t.dist.2t function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n}_D}} \\ & = & \frac{3.714...-0}{\frac{4.498...}{\sqrt{7}}} \\ & = & 2.184... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n_D-1=7-1=6[/latex].
| Function | t.dist.2t | Answer |
| Field 1 | 2.184.... | 0.0716 |
| Field 2 | 6 |
So the p-value[latex]=0.0716[/latex].
Conclusion:
Because p-value[latex]=0.0716 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that there a difference in the average distance for the dominant versus weaker hand.
NOTES
- Before writing down the hypotheses, decide on the order of subtraction for calculating the differences. In a matched sample experiment, the form of the alternative hypothesis depends on order of subtraction, so we must decide on the order of subtraction before writing down the hypotheses.
- The null hypothesis [latex]\mu_D=0[/latex] is the claim that there is no difference in the average distance. That is, the average distance is the same for both hands.
- For the alternative hypothesis, we are testing that there is a difference in the dominant hand and weaker hand distances. In other words, dominant≠weaker. So, the alternative hypothesis is [latex]\mu_D \neq 0[/latex], the claim that there is a difference in the distances.
- Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p-value. This ensures that we get the most accurate value for the p-value. Use Excel to do the calculations, and then click on the cells in subsequent calculations.
- The p-value of 0.0716 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, on average, the distances are the same for both hands.
Watch this video: Hypothesis Testing for Matched/Paired Samples by ExcelIsFun [20:48]
Concept Review
The general form of a confidence interval for the mean difference of matched samples is
[latex]\begin{eqnarray*} \\ \mbox{Lower Limit} & = & \overline{x}_D-t \times \frac{s_D}{\sqrt{n_D}} \\ \\\mbox{Upper Limit} & = & \overline{x}_D+t \times \frac{s_D}{\sqrt{n_D}} \\ \\ \end{eqnarray*}[/latex]
where [latex]t[/latex] is the positive [latex]t[/latex]-score of the [latex]t[/latex]-distribution with [latex]n_D-1[/latex] degrees of freedom so the area under the [latex]t[/latex]-distribution in between [latex]-t[/latex] and [latex]t[/latex] is [latex]C[/latex].
The hypothesis test for matched samples is a well established process:
- Write down the null and alternative hypotheses in terms of the mean difference [latex]\mu_D[/latex].
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- Find the p-value (the area in the corresponding tail) for the test using the [latex]t[/latex]-distribution. Because the population standard deviation is unknown, we use the [latex]t[/latex]-distribution to find the p-value with [latex]\displaystyle{t=\frac{\overline{x}_D-\mu_D}{\frac{s_D}{\sqrt{n_D}}}}[/latex] and [latex]\displaystyle{df=n_D-1}[/latex].
- Compare the p-value to the significance level and state the outcome of the test.
- Write down a concluding sentence specific to the context of the question.
Attribution
"10.4 Matched or Paired Samples" in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.




