3.8 Exercises
1. In a particular college class, there are male and female students. Some students have long hair and some students have short hair. Write the symbols for the probabilities of the events for parts a through j. (Note that you cannot find numerical answers here. You were not given enough information to find any probability values yet; concentrate on understanding the symbols.)
- Let F be the event that a student is female.
- Let M be the event that a student is male.
- Let S be the event that a student has short hair.
- Let L be the event that a student has long hair.
- The probability that a student does not have long hair.
- The probability that a student is male or has short hair.
- The probability that a student is a female and has long hair.
- The probability that a student is male, given that the student has long hair.
- The probability that a student has long hair, given that the student is male.
- Of all the female students, the probability that a student has short hair.
- Of all students with long hair, the probability that a student is female.
- The probability that a student is female or has long hair.
- The probability that a randomly selected student is a male student with short hair.
- The probability that a student is female.
2. A box is filled with several party favors. It contains 12 hats, 15 noisemakers, ten finger traps, and five bags of confetti. Let [latex]H[/latex] be the event of getting a hat. Let [latex]N[/latex] be the event of getting a noisemaker. Let [latex]F[/latex] be the event of getting a finger trap. Let [latex]C[/latex] be the event of getting a bag of confetti.
- Find [latex]P(H)[/latex].
- Find [latex]P(N)[/latex].
- Find [latex]P(F)[/latex].
- Find [latex]P(C)[/latex].
3. A jar of 150 jelly beans contains 22 red jelly beans, 38 yellow, 20 green, 28 purple, 26 blue, and the rest are orange.
- Let [latex]B[/latex]= the event of getting a blue jelly bean
- Let [latex]G[/latex] = the event of getting a green jelly bean.
- Let [latex]O[/latex] = the event of getting an orange jelly bean.
- Let [latex]P[/latex] = the event of getting a purple jelly bean.
- Let [latex]R[/latex] = the event of getting a red jelly bean.
- Let [latex]Y[/latex] = the event of getting a yellow jelly bean.
- Find [latex]P(B)[/latex].
- Find [latex]P(G)[/latex].
- Find [latex]P(P)[/latex].
- Find [latex]P(R)[/latex].
- Find [latex]P(Y)[/latex].
4.There are 23 countries in North America, 12 countries in South America, 47 countries in Europe, 44 countries in Asia, 54 countries in Africa, and 14 in Oceania (Pacific Ocean region).
- Let [latex]A[/latex] = the event that a country is in Asia.
- Let [latex]E[/latex] = the event that a country is in Europe.
- Let [latex]F[/latex] = the event that a country is in Africa.
- Let [latex]N[/latex] = the event that a country is in North America.
- Let [latex]O[/latex] = the event that a country is in Oceania.
- Let [latex]S[/latex]= the event that a country is in South America.
- Find [latex]P(A)[/latex].
- Find [latex]P(E)[/latex].
- Find [latex]P(F)[/latex].
- Find [latex]P(N)[/latex].
- Find [latex]P(O)[/latex].
- Find [latex]P(S)[/latex].
5. What is the probability of drawing a red card from a standard deck of 52 cards?
6. What is the probability of drawing a club in a standard deck of 52 cards?
7. What is the probability of rolling an even number of dots with a fair, six-sided die numbered one through six?
8. What is the probability of rolling a prime number of dots with a fair, six-sided die numbered one through six?
9. On a baseball team, there are infielders and outfielders. Some players are great hitters, and some players are not great hitters.
- Let [latex]I[/latex] = the event that a player in an infielder.
- Let [latex]O[/latex] = the event that a player is an outfielder.
- Let [latex]H[/latex] = the event that a player is a great hitter.
- Let [latex]N[/latex] = the event that a player is not a great hitter.
- Write the symbols for the probability that a player is not an outfielder.
- Write the symbols for the probability that a player is an outfielder or is a great hitter.
- Write the symbols for the probability that a player is an infielder and is not a great hitter.
- Write the symbols for the probability that a player is a great hitter, given that the player is an infielder.
- Write the symbols for the probability that a player is an infielder, given that the player is a great hitter.
- Write the symbols for the probability that of all the outfielders, a player is not a great hitter.
- Write the symbols for the probability that of all the great hitters, a player is an outfielder.
- Write the symbols for the probability that a player is an infielder or is not a great hitter.
- Write the symbols for the probability that a player is an outfielder and is a great hitter.
- Write the symbols for the probability that a player is an infielder.
10. What is the word for the set of all possible outcomes?
11. What is conditional probability?
12. You are rolling a fair, six-sided number cube. Let [latex]E[/latex]= the event that it lands on an even number. Let [latex]M[/latex]= the event that it lands on a multiple of three.
- What does [latex]P(E|M)[/latex] mean in words?
- What does [latex]P(E \mbox{ or }M)[/latex] mean in words?
13. Explain what is wrong with the following statements. Use complete sentences.
- If there is a 60% chance of rain on Saturday and a 70% chance of rain on Sunday, then there is a 130% chance of rain over the weekend.
- The probability that a baseball player hits a home run is greater than the probability that he gets a successful hit.
14. [latex]E[/latex] and [latex]F[/latex] are mutually exclusive events. [latex]P(E) = 0.4[/latex]; [latex]P(F) = 0.[/latex]5. Find [latex]P(E∣F)[/latex].
15. [latex]J[/latex] and [latex]K[/latex] are independent events. [latex]P(J|K) = 0.3[/latex]. Find [latex]P(J)[/latex].
16. [latex]U[/latex] and [latex]V[/latex]are mutually exclusive events. [latex]P(U) = 0.26[/latex]; [latex]P(V) = 0.37[/latex]. Find:
- [latex]P(U \mbox{ and } V)[/latex]
- [latex]P(U|V) [/latex]
- [latex]P(U \mbox{ or } V)[/latex]
17. [latex]Q[/latex] and [latex]R[/latex] are independent events. [latex]P(Q) = 0.4[/latex] and [latex]P(Q \mbox{ and } R) = 0.1[/latex]. Find [latex]P(R)[/latex].
18. A previous year, the weights of the members of the San Francisco 49ers and the Dallas Cowboys were published in the San Jose Mercury News. The factual data are compiled into the table.
| Shirt Number | At most 210 | 211–250 | 251–290 | More than 290 | Total |
| 1–33 | 21 | 5 | 0 | 0 | 26 |
| 34–66 | 6 | 18 | 7 | 4 | 35 |
| 66–99 | 6 | 12 | 22 | 5 | 45 |
| Total | 33 | 35 | 29 | 9 | 106 |
For the following, suppose that you randomly select one player from the 49ers or Cowboys.
- What is the probability that the player's shirt number is in the 34-66 category?
- What is the probability that the player weighs at most 210 lbs?
- What is the probability that the player's shirt number is in the 1-33 category and weighs between 211 and 250 lbs?
- What is the probability that the player's shirt number is in the 66-99 category or weights more than 290 lbs?
- What is the probability that the player's shirt number is in the 34-66 category given that they weigh between 251 and 290 lbs?
- What is the probability that a player weights at most 210 lbs if their shirt number is in the 1-33 category?
- Are the events "66-99" and more than 290 lbs independent? Explain.
19. At a local college, 20% of the students are studying business, 40% of the students are studying mathematics and 8% of the students are studying both business and mathematics.
- What is the probability that a randomly selected student studies business or mathematics?
- What is the probability that a randomly selected student studies mathematics given that they study business?
- What is the probability that a randomly selected mathematics student studies business?
- Are the events "business" and "mathematics" independent? Explain.
- Are the events "business" and "mathematics" mutually exclusive? Explain.
20. The casino game, roulette, allows the gambler to bet on the probability of a ball, which spins in the roulette wheel, landing on a particular color, number, or range of numbers. The table used to place bets contains of 38 numbers (0,00, 1, 2,...,36), and each number is assigned to a color (green, red or black) and a range. You can place a bet based on number, color, or range.
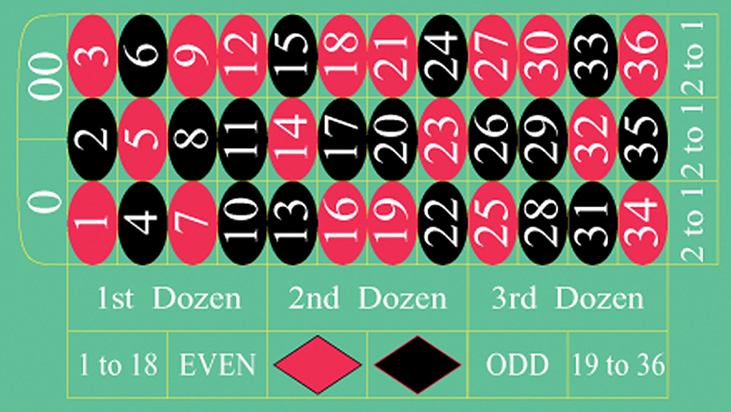
- List the sample space of the 38 possible outcomes in roulette.
- You bet on red. Find the probability of red.
- You bet on "1st Dozen" (meaning the number from 1 to 12). Find the probability of "1st Dozen".
- You bet on an even number. Find the probability of an even number.
- Is getting an odd number the complement of getting an even number? Why?
- Find two mutually exclusive events.
- Are the events "Even" and "1st Dozen" independent? Explain.
- What is the probability of the event "1 to 18"?
21. Suppose that you have eight cards. Five are green and three are yellow. The five green cards are numbered 1, 2, 3, 4, and 5. The three yellow cards are numbered 1, 2, and 3. The cards are well shuffled. You randomly draw one card.
- What is the probability the card is green?
- What is the probability the card is green given that the card has an even number on it?
- What is the probability the card is green or has an even number on it?
- What is the probability the card is green and has an even number on it?
- Are the events "green" and "even" mutually exclusive? Explain.
- Are the events "green and "even" independent? Explain..
22. A special deck of cards has ten cards. Four are green, three are blue, and three are red. When a card is picked, its color of it is recorded.
- Suppose three cards are picked without replacement. What is the probability that all three cards are green?
- Suppose three cards are picked without replacement. What is the probability that exactly two of the cards are blue?
- Suppose three cards are picked without replacement. What is the probability that at least one of the cards is red?
- Suppose three cards are picked with replacement. What is the probability that at most one card is green?
- Suppose three cards are picked with replacement. What is the probability that all three cards are green?
- Suppose three cards are picked with replacement. What is the probability that exactly two of the cards are blue?
- Suppose three cards are picked with replacement. What is the probability that at least one of the cards is red?
- Suppose three cards are picked with replacement. What is the probability that at most one card is green?
23. Suppose [latex]P(C) = 0.4[/latex], [latex]P(D) = 0.5[/latex] and [latex]P(C|D) = 0.6[/latex].
- Find [latex]P(C \mbox{ and }D)[/latex].
- Are [latex]C[/latex] and[latex]D[/latex] mutually exclusive? Why or why not?
- Are [latex]C[/latex] and [latex]D[/latex] independent events? Why or why not?
- Find [latex]P( \mbox{ or } D)[/latex].
- Find [latex]P(D|C)[/latex].
24. In 1994, the U.S. government held a lottery to issue 55,000 Green Cards (permits for non-citizens to work legally in the U.S.). Renate Deutsch, from Germany, was one of approximately 6.5 million people who entered this lottery.
- What was Renate’s chance of winning a Green Card? Write your answer as a probability statement.
- In the summer of 1994, Renate received a letter stating she was one of 110,000 finalists chosen. Once the finalists were chosen, assuming that each finalist had an equal chance to win, what was Renate’s chance of winning a Green Card? Write your answer as a conditional probability statement.
- Are "won a green card" and "finalist" independent or dependent events? Justify your answer numerically and also explain why.
- Are "won a green card" and "finalist" mutually exclusive events? Justify your answer numerically and explain why.
25. The following table of data obtained from www.baseball-almanac.com shows hit information for four players. Suppose that one hit from the table is randomly selected.
| Name | Single | Double | Triple | Home Run | Total Hits |
|---|---|---|---|---|---|
| Babe Ruth | 1,517 | 506 | 136 | 714 | 2,873 |
| Jackie Robinson | 1,054 | 273 | 54 | 137 | 1,518 |
| Ty Cobb | 3,603 | 174 | 295 | 114 | 4,189 |
| Hank Aaron | 2,294 | 624 | 98 | 755 | 3,771 |
| Total | 8,471 | 1,577 | 583 | 1,720 | 12,351 |
- Are "the hit being made by Hank Aaron" and "the hit being a double" independent events? Explain.
- What is the probability that a hit was made by Babe Ruth?
- What is the probability that a hit was made by Hank Aaron and is a home run?
- What is the probability that a hit was made by Ty Cobb or is a single?
- What is the probability that a hit was a double given that it was by Jackie Robinson?
- What is the probability that a triple was hit by Babe Ruth?
26. United Blood Services is a blood bank that serves more than 500 hospitals in 18 states. According to their website, a person with type O blood and a negative Rh factor (Rh-) can donate blood to any person with any bloodtype. Their data show that 43% of people have type O blood and 15% of people have Rh- factor; 52% of people have type O or Rh- factor.
- Find the probability that a person has both type O blood and the Rh- factor.
- Find the probability that a person does NOT have both type O blood and the Rh- factor.
27. At a college, 72% of courses have final exams and 46% of courses require research papers. Suppose that 32% of courses have a research paper and a final exam.
- Find the probability that a course has a final exam or a research project.
- Find the probability that a course has NEITHER of these two requirements.
28. In a box of assorted cookies, 36% contain chocolate and 12% contain nuts. Of those, 8% contain both chocolate and nuts. Sean is allergic to both chocolate and nuts.
- Find the probability that a cookie contains chocolate or nuts (he can't eat it).
- Find the probability that a cookie does not contain chocolate or nuts (he can eat it).
29. A college finds that 10% of students have taken a distance learning class and that 40% of students are part time students. Of the part time students, 20% have taken a distance learning class. Let D = event that a student takes a distance learning class and E = event that a student is a part time student.
- Find the probability that a student takes a distance learning class and is a part-time student.
- Find the probability that a student is a part-time student given that they take a distance learning class.
- Find the probability that student is a part-time student or takes a distance learning class.
- Are the events "distance learning" and "part-time" independent? Explain.
30. The table shows a random sample of musicians and how they learned to play their instruments.
| Gender | Self-taught | Studied in School | Private Instruction | Total |
|---|---|---|---|---|
| Female | 12 | 38 | 22 | 72 |
| Male | 19 | 24 | 15 | 58 |
| Total | 31 | 62 | 37 | 130 |
- Find the probability a musician is female.
- Find the probability that a musician received private instruction.
- Find the probability that a musician is male and is self-taught.
- Find the probability that a musician is female or studied in school.
- Find the probability that a musician is male given that they received private instruction.
- Find the probability that a female musician is self-taught.
- Are the events "female" and "self-taught" independent? Explain.
31. The table shows the political party affiliation of each of 67 members of the US Senate in June 2012, and when they are up for reelection.
| Up for reelection: | Democratic Party | Republican Party | Other | Total |
|---|---|---|---|---|
| November 2014 | 20 | 13 | 0 | |
| November 2016 | 10 | 24 | 0 | |
| Total |
- What is the probability that a randomly selected senator has an “Other” affiliation?
- What is the probability that a randomly selected senator is up for reelection in November 2016?
- What is the probability that a randomly selected senator is a Democrat and up for reelection in November 2016?
- What is the probability that a randomly selected senator is a Republican or is up for reelection in November 2014?
- Suppose that a member of the US Senate is randomly selected. Given that the randomly selected senator is up for reelection in November 2016, what is the probability that this senator is a Democrat?
- Suppose that a member of the US Senate is randomly selected. What is the probability that the senator is up for reelection in November 2014, knowing that this senator is a Republican?
32. Table identifies a group of children by one of four hair colors, and by type of hair.
| Hair Type | Brown | Blond | Black | Red | Totals |
|---|---|---|---|---|---|
| Wavy | 20 | 15 | 3 | 43 | |
| Straight | 80 | 15 | 12 | ||
| Totals | 20 | 215 |
- Complete the table.
- What is the probability that a randomly selected child will have wavy hair?
- What is the probability that a randomly selected child will have either brown or blond hair?
- What is the probability that a randomly selected child will have wavy brown hair?
- What is the probability that a randomly selected child will have red hair, given that he or she has straight hair?
- If B is the event of a child having brown hair, find the probability of the complement of B.
- In words, what does the complement of B represent?
33. A box of cookies contains three chocolate and seven butter cookies. Miguel randomly selects a cookie and eats it. Then he randomly selects another cookie and eats it. (How many cookies did he take?)
- Let [latex]S[/latex] be the event that both cookies selected were the same flavor. Find [latex]P(S)[/latex].
- Let [latex]T[/latex] be the event that the cookies selected were different flavors. Find [latex]P(T)[/latex].
- Let [latex]U[/latex] be the event that the second cookie selected is a butter cookie. Find [latex]P(U)[/latex].
34. A cup contains three red, four yellow and five blue beads.
- Suppose three beads are selected at random without replacement. What is the probability all three beads are blue?
- Suppose three beads are selected at random with replacement. What is the probability all three beads are blue?
- Suppose three beads are selected at random without replacement. What is the probability that exactly one of the beads is red?
- Suppose three beads are selected at random with replacement. What is the probability that exactly one of the beads is red?
- Suppose three beads are selected at random without replacement. What is the probability that at least one bead is yellow?
- Suppose three beads are selected at random with replacement. What is the probability that at least one bead is yellow?
35. The percent of licensed U.S. drivers (from a recent year) that are female is 48.60. Of the females, 5.03% are age 19 and under; 81.36% are age 20–64; 13.61% are age 65 or over. Of the licensed U.S. male drivers, 5.04% are age 19 and under; 81.43% are age 20–64; 13.53% are age 65 or over.
- Find the probability a driver is female.
- Find the probability a driver is 65 or over given that they are female.
- Find the probability a driver is 65 or over and female.
- In words, explain the difference between the probabilities in part c and part d.
- Find the probability a driver is 65 or over.
- Are being age 65 or over and being female mutually exclusive events? How do you know?
36. Approximately 86.5% of Americans commute to work by car, truck, or van. Out of that group, 84.6% drive alone and 15.4% drive in a carpool. Approximately 3.9% walk to work and approximately 5.3% take public transportation.
- Assuming that the walkers walk alone, what percent of all commuters travel alone to work?
- Suppose that 1,000 workers are randomly selected. How many would you expect to travel alone to work?
- Suppose that 1,000 workers are randomly selected. How many would you expect to drive in a carpool?
37. When the Euro coin was introduced in 2002, two math professors had their statistics students test whether the Belgian one Euro coin was a fair coin. They spun the coin rather than tossing it and found that out of 250 spins, 140 showed a head (event [latex]H[/latex]) while 110 showed a tail (event [latex]T[/latex]). On that basis, they claimed that it is not a fair coin.
- Based on the given data, find [latex]P(H)[/latex] and [latex]P(T)[/latex].
- Find the probabilities of each possible outcome for the experiment of tossing the coin twice.
- Find the probability of obtaining exactly one head in two tosses of the coin.
- Find the probability of obtaining at least one head.
Attribution
"Chapter 3 Homework" and "Chapter 3 Practice" in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.

