3.4 The Complement Rule
LEARNING OBJECTIVES
- Calculate probabilities using the complement rule.
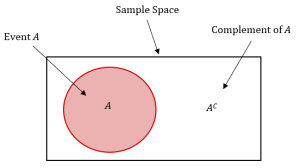
The complement of an event [latex]A[/latex] is the set of all outcomes in the sample space that are not in [latex]A[/latex]. The complement of [latex]A[/latex] is denoted by [latex]A^C[/latex] and is read "not [latex]A[/latex]."
EXAMPLE
Suppose a coin is flipped two times. Previously, we found the sample space for this experiment: [latex]S=\{HH, HT, TH, TT\}[/latex] where [latex]H[/latex] is heads and [latex]T[/latex] is tails.
- What is the complement of the event "exactly one head"?
- What is the complement of the event "at least one tail."
Solution:
- The event "exactly one head" consists of the outcomes [latex]HT[/latex] and [latex]TH[/latex]. The complement of "exactly one head" consists of the outcomes [latex]HH[/latex] and [latex]TT[/latex]. These are the outcomes in the sample space [latex]S[/latex] that are NOT in the original event "exactly one head."
- The event "at least one tail" consists of the outcomes [latex]HT[/latex], [latex]TH[/latex], and [latex]TT[/latex]. The complement of "at least one tail" consists of the outcomes [latex]HH[/latex]. These are the outcomes in the sample space [latex]S[/latex] that are NOT in the original event "at least one tail."
TRY IT
Suppose you roll a fair six-sided die with the numbers [latex]1, 2, 3, 4, 5, 6[/latex] on the faces. Previously, we found the sample space for this experiment: [latex]S=\{1,2,3,4,5,6\}[/latex]
- What is the complement of the event "rolling a 4"?
- What is the complement of the event "rolling a number greater than or equal to 5"?
- What is the complement of the event "rolling a even number"?
- What is the complement of the event "rolling a number less than 4"?
Click to see Solution
- The complement is [latex]\{1,2,3,5,6\}[/latex].
- The complement is [latex]\{1,2,3,4\}[/latex].
- The complement is [latex]\{1,3,5\}[/latex].
- The complement is [latex]\{1,2,3,4\}[/latex].
The Probability of the Complement
In any experiment, an event [latex]A[/latex] or its complement [latex]A^C[/latex] must occur. This means that [latex]\displaystyle{P(A)+P(A^C)=1}[/latex]. Rearranging this equation gives us a formula for finding the probability of the complement from the original event:
[latex]\begin{eqnarray*}P(A^C)&=&1-P(A)\\\\\end{eqnarray*}[/latex]
EXAMPLE
An online retailer knows that 30% of customers spend more than $100 per transaction. What is the probability that a customer spends at most $100 per transaction?
Solution:
Spending at most $100 ($100 or less) per transaction is the complement of spending more than $100 per transaction.
[latex]\begin{eqnarray*} P(\mbox{at most \$100}) & = & 1-P(\mbox{more than \$100}) \\ & = & 1-0.3 \\ & = & 0.7 \end{eqnarray*}[/latex]
TRY IT
At a local college, a statistics professor has a class of 80 students. After polling the students in the class, the professor finds out that 15 of the students play on one of the school's sports team and 60 of the students have part-time jobs.
- What is the probability that a student in the class does not play on one of the school's sports teams?
- What is the probability that a student in the class does not have a part-time job?
Click to see Solution
- [latex]\displaystyle{P(\mbox{no sports team})=1-P(\mbox{sports team})=1-\frac{15}{80}=0.8125}[/latex]
- [latex]\displaystyle{P(\mbox{no part-time job})=1-P(\mbox{part-time job})=1-\frac{60}{80}=0.25}[/latex]
Concept Review
The complement, [latex]A^C[/latex], of an event [latex]A[/latex] consists of all of the outcomes in the sample space that are NOT in event [latex]A[/latex]. The probability of the complement can be found from the original event using the formula: [latex]\displaystyle{P(A^C)=1-P(A)}[/latex].
Attribution
"3.1 Terminology" in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.