12.2 Linear Equations

LEARNING OBJECTIVES

  • Identify a linear equation, graphically or algebraically.

In this chapter we will be studying simple linear regression, which models the linear relationship between two variables [latex]x[/latex] and [latex]y[/latex].  A linear equation has the form [latex]y=b_0+b_1x[/latex] where [latex]b_0[/latex] is the [latex]y[/latex]-intercept of the line and [latex]b_1[/latex] is the slope of the line.  For example, [latex]y=3+2x[/latex] and [latex]y=1-4x[/latex] are examples of linear equations.  The graph of linear equation is a straight line.

EXAMPLE

The equation [latex]y=-1+2x[/latex] is a linear equation.  The slope is [latex]2[/latex] and the [latex]y[/latex]-intercept is [latex]-1[/latex].  The graph of [latex]y=-1+2x[/latex] is shown below.

Graph of the equation y = -1 + 2x. This is a straight line that crosses the y-axis at -1 and is sloped up and to the right, rising 2 units for every one unit of run.

TRY IT

Is the graph shown below the graph of a linear equation?  Why or why not?

This is a graph of an equation. The x-axis is labeled in intervals of 2 from 0 - 14; the y-axis is labeled in intervals of 2 from 0 - 12. The equation's graph is a curve that crosses the y-axis at 2 and curves upward and to the right.

Click to see Solution

 

This is not a linear equation because the graph is not a straight line.

The slope [latex]b_1[/latex] is a number that describes the steepness of a line.  The slope tells us how the value of the [latex]y[/latex] variable will change for every one unit increase in the value of the [latex]x[/latex] variable.

The [latex]y[/latex]-intercept is the value of the [latex]y[/latex]-coordinate where the line crosses the [latex]y[/latex]-axis.  Algebraically, the [latex]y[/latex]-intercept is the value of [latex]y[/latex] when [latex]x=0[/latex].

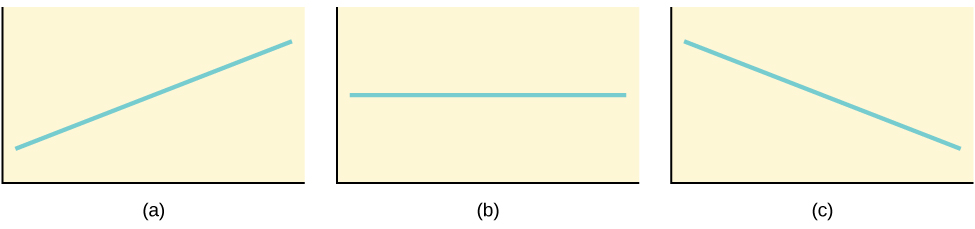
Consider the figure below, which illustrates three different linear equations:

  • In (a), the line rises from left to right across the graph.  This means that the slope [latex]b_1[/latex] is a positive number ([latex]b_1 \gt 0[/latex]).
  • In (b), the line is horizontal (parallel to the [latex]x[/latex]-axis).  This means that the slope [latex]b_1[/latex] is zero ([latex]b_1=0[/latex]).
  • In (c), the line falls from left to right across the graph.  This means that the slope [latex]b_1[/latex] is a negative number ([latex]b_1 \lt 0[/latex]).

 

Three possible graphs of the equation y = a + bx. For the first graph, (a), b > 0 and so the line slopes upward to the right. For the second, b = 0 and the graph of the equation is a horizontal line. In the third graph, (c), b < 0 and the line slopes downward to the right. 0 and so the line slopes upward to the right. For the second, b = 0 and the graph of the equation is a horizontal line. In the third graph, (c), b

EXAMPLE

Consider the linear equation [latex]y=-25+15x[/latex].

  • The slope is [latex]15[/latex].  This tells us that when the value of [latex]x[/latex] increases by [latex]1[/latex], the value of [latex]y[/latex] increases by [latex]15[/latex].  Because the slope is positive, the graph of [latex]y=-25+15x[/latex] rises from left to right.
  • The [latex]y[/latex]-intercept is [latex]-25[/latex].  This tells us that when [latex]x=0[/latex], [latex]y=-25[/latex].  On the graph of [latex]y=-25+15x[/latex], the line crosses the [latex]y[/latex]-axis at [latex]-25[/latex].

TRY IT

Consider the linear equation [latex]y=17-10x[/latex].  Identify the slope and [latex]y[/latex]-intercept.  Describe the slope and [latex]y[/latex]-intercept in sentences.

 

Click to see Solution
  • The slope is [latex]-10[/latex].  This tells us that when the value of [latex]x[/latex] increases by [latex]1[/latex], the value of [latex]y[/latex] decreases by [latex]10[/latex].  Because the slope is negative, the graph of [latex]y=17-10x[/latex] falls from left to right.
  • The [latex]y[/latex]-intercept is [latex]17[/latex].  This tells us that when [latex]x=0[/latex], [latex]y=17[/latex].  On the graph of [latex]y=17-10x[/latex], the line crosses the [latex]y[/latex]-axis at [latex]17[/latex].

Concept Review

The most basic type of association is a linear association.  This type of relationship can be defined algebraically by the equation used, numerically with actual or predicted data values, or graphically from a plotted curve (lines are classified as straight curves).  Algebraically, a linear equation typically takes the form [latex]y=b_0+b_1x[/latex], where [latex]b_0[/latex] is the [latex]y[/latex]-intercept and [latex]b_1[/latex] is the slope.

The slope is a value that describes the rate of change of the [latex]y[/latex] variable for a single unit increase in the [latex]x[/latex] variable.  The [latex]y[/latex]-intercept is the value of [latex]y[/latex] when [latex]x=0[/latex].

Attribution

“12.1 Linear Equations” in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.