10.3 Statistical Inference for a Single Population Variance

LEARNING OBJECTIVES

  • Calculate and interpret a confidence interval for a population variance.
  • Conduct and interpret a hypothesis test on a single population variance.

The mean of a population is important, but in many cases the variance of the population is just as important.  In most production processes, quality is measured by how closely the process matches the target (i.e. the mean) and by the variability (i.e. the variance) of the process.  For example, if a process is to fill bags of coffee beans, we are interested in both the average weight of the bag and how much variation there is in the weight of the bags.  The quality is considered poor if the average weight of the bags is accurate but the variance of the weight of the bags is too high—a variance that is too large means some bags would be too full and some bags would be almost empty.

As with other population parameters, we can construct a confidence interval to capture the population variance and conduct a hypothesis test on the population variance.  In order to construct a confidence interval or conduct a hypothesis test on a population variance [latex]\sigma^2[/latex], we need to use the distribution of [latex]\displaystyle{\frac{(n-1) \times s^2}{\sigma^2}}[/latex].  Suppose we have a normal population with population variance [latex]\sigma^2[/latex] and a sample of size [latex]n[/latex] is taken from the population.  The sampling distribution of [latex]\displaystyle{\frac{(n-1) \times s^2}{\sigma^2}}[/latex] follows a [latex]\chi^2[/latex]-distribution with [latex]n-1[/latex] degrees of freedom.

Constructing a Confidence Interval for a Population Variance

To construct the confidence interval, take a random sample of size [latex]n[/latex] from a normally distributed population.  Calculate the sample variance [latex]s^2[/latex].  The limits for the confidence interval with confidence level [latex]C[/latex] for an unknown population variance [latex]\sigma^2[/latex] are

[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & \frac{(n-1) \times s^2}{\chi^2_R} \\ \\ \mbox{Upper Limit} & = & \frac{(n-1) \times s^2}{\chi^2_L} \\ \\  \end{eqnarray*}[/latex]

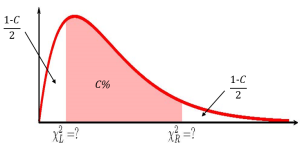
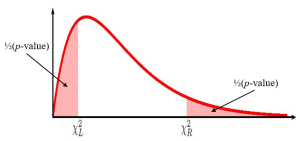
where [latex]\chi^2_L[/latex] is the [latex]\chi^2[/latex]-score so that the area in the left-tail of the [latex]\chi^2[/latex]-distribution is [latex]\displaystyle{\frac{1-C}{2}}[/latex],  [latex]\chi^2_R[/latex] is the [latex]\chi^2[/latex]-score so that the area in the right-tail of the [latex]\chi^2[/latex]-distribution is [latex]\displaystyle{\frac{1-C}{2}}[/latex] and the [latex]\chi^2[/latex]-distribution has [latex]n-1[/latex] degrees of freedom.

This is a chi square distribution. Along the horizontal axis the points chi square L and chi square R are labeled. The area under the curve in between chi square L and chi square R equals C%. The area in the right tail to the right of chi square R equals (1-C)/2. The area in the left tail to the left of chi square L equals (1-C)/2.

NOTES

  1. Like the other confidence intervals we have seen, the [latex]\chi^2[/latex]-scores are the values that trap [latex]C\%[/latex] of the observations in the middle of the distribution so that the area of each tail is [latex]\displaystyle{\frac{1-C}{2}}[/latex].
  2. Because the [latex]\chi^2[/latex]-distribution is not symmetrical, the confidence interval for a population variance requires that we calculate two different [latex]\chi^2[/latex]-scores:  one for the left tail and one for the right tail.  In Excel, we will need to use both the chisq.inv function (for the left tail) and the chisq.inv.rt function (for the right tail) to find the two different [latex]\chi^2[/latex]-scores.
  3. The [latex]\chi^2[/latex]-score for the left tail is part of the formula for the upper limit and the [latex]\chi^2[/latex]-score for the right tail is part of the formula for the lower limit.  This is not a mistake.  It follows from the formula used to determine the limits for the confidence interval.

EXAMPLE

A local telecom company conducts broadband speed tests to measure how much data per second passes between a customer’s computer and the internet compared to what the customer pays for as part of their plan .  The company needs to estimate the variance in the broadband speed.  A sample of 15 ISPs is taken and amount of data per second is recorded.  The variance in the sample is 174.

  1. Construct a 97% confidence interval for the variance in the amount of data per second that passes between a customer’s computer and the internet.
  2. Interpret the confidence interval found in part 1.

Solution:

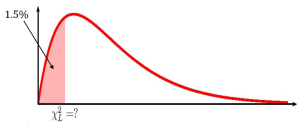
  1. To find the confidence interval, we need to find the [latex]\chi^2_L[/latex]-score for the 97% confidence interval.  This means that we need to find the [latex]\chi^2_L[/latex]-score so that the area in the left tail is [latex]\displaystyle{\frac{1-0.97}{2}=0.015}[/latex].  The degrees of freedom for the [latex]\chi^2[/latex]-distribution is [latex]n-1=15-1=14[/latex].

    This is a chi square distribution. Along the horizontal axis the point chi square L is labeled. The area in the left tail to the left of chi square L equals 1.5%

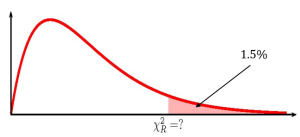
    Function chisq.inv Answer
    Field 1 0.015 5.0572…
    Field 2 14

    We also need find the [latex]\chi^2_R[/latex]-score for the 97% confidence interval.  This means that we need to find the [latex]\chi^2_R[/latex]-score so that the area in the right tail is [latex]\displaystyle{\frac{1-0.97}{2}=0.015}[/latex].  The degrees of freedom for the [latex]\chi^2[/latex]-distribution is [latex]n-1=15-1=14[/latex].

    This is a chi square distribution. Along the horizontal axis the point chi square R is labeled. The area in the left tail to the left of chi square R equals 1.5%

    Function chisq.inv.rt Answer
    Field 1 0.015 27.826…
    Field 2 14

    So [latex]\chi^2_L=5.0572...[/latex] and [latex]\chi^2_R=27.826...[/latex].  From the sample data supplied in the question [latex]s^2=174[/latex] and [latex]n=15[/latex].  The 97% confidence interval is

    [latex]\begin{eqnarray*} \mbox{Lower Limit} & = & \frac{(n-1) \times s^2}{\chi^2_R} \\ & = & \frac{(15-1) \times 174}{27.826...} \\ & = & 87.54  \\ \\ \mbox{Upper Limit} & = & \frac{(n-1) \times s^2}{\chi^2_R} \\ & = & \frac{(15-1) \times 174}{5.0572...} \\ & = & 481.69 \\ \\ \end{eqnarray*}[/latex]

  2. We are 97% confident that the variance in the amount of data per second that passes between a customer’s computer and the internet is between 87.54 and 481.69.

NOTES

  1. When calculating the limits for the confidence interval keep all of the decimals in the [latex]\chi^2[/latex]-scores and other values throughout the calculation.  This will ensure that there is no round-off error in the answer.  You can use Excel to do the calculations of the limits, clicking on the cells containing the [latex]\chi^2[/latex]-scores and any other values.
  2. When writing down the interpretation of the confidence interval, make sure to include the confidence level and the actual population variance captured by the confidence interval (i.e. be specific to the context of the question).  In this case, there are no units for the limits because variance does not have any limits.

Steps to Conduct a Hypothesis Test for a Population Variance

  1. Write down the null and alternative hypotheses in terms of the population variance [latex]\sigma^2[/latex].
  2. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
  3. Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
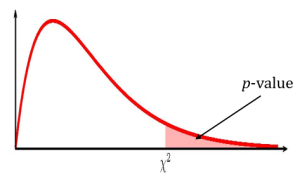
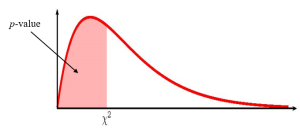
  4. Use the [latex]\chi^2[/latex]-distribution to find the p-value (the area in the corresponding tail) for the test.  The [latex]\chi^2[/latex]-score and degrees of freedom are

    [latex]\begin{eqnarray*}\chi^2=\frac{(n-1) \times s^2}{\sigma^2} & \; \; \; \; \; \; \; \; & df=n-1 \\ \\ \end{eqnarray*}[/latex]

  5. Compare the p-value to the significance level and state the outcome of the test:
    • If p-value[latex]\leq \alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
      • The results of the sample data are significant.  There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
    • If p-value[latex]\gt \alpha[/latex], do not reject [latex]H_0[/latex].
      • The results of the sample data are not significant.  There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
  6. Write down a concluding sentence specific to the context of the question.

EXAMPLE

A statistics instructor at a local college claims that the variance for the final exam scores was 25.  After speaking with his classmates, one the class’s best students thinks that the variance for the final exam scores is higher than the instructor claims.  The student challenges the instructor to prove her claim.  The instructor takes a sample 30 final exams and finds the variance of the scores is 28.  At the 5% significance level, test if the variance of the final exam scores is higher than the instructor claims.

Solution:

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \sigma^2=25  \\ H_a: & & \sigma^2 \gt 25 \end{eqnarray*}[/latex]

p-value: 

From the question, we have [latex]n=30[/latex], [latex]s^2=28[/latex], and [latex]\alpha=0.05[/latex].

Because the alternative hypothesis is a [latex]\gt[/latex], the p-value is the area in the right tail of the [latex]\chi^2[/latex]-distribution.

This is a chi square distribution. Along the horizontal axis the point chi square is labeled. The area in the right tail to the right of chi square is shaded and labeled with p-value.

To use the chisq.dist.rt function, we need to calculate out the [latex]\chi^2[/latex]-score and the degrees of freedom:

[latex]\begin{eqnarray*} \chi^2 & = &\frac{(n-1) \times s^2}{\sigma^2} \\ & = & \frac{(30-1) \times 28}{25} \\ & = & 32.48 \\ \\ df & = & n-1 \\ & = & 30-1 \\ & = & 29 \end{eqnarray*}[/latex]

Function  chisq.dist.rt Answer
Field 1 32.48 0.2992
Field 2 29

So the p-value[latex]=0.2992[/latex].

Conclusion:

Because p-value[latex]=0.2992 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that the variance of the final exam scores is higher than 25.

NOTES

  1. The null hypothesis [latex]\sigma^2=25[/latex] is the claim that the variance on the final exam is 25.
  2. The alternative hypothesis [latex]\sigma^2 \gt 25[/latex] is the claim that the variance on the final exam is greater than 25.
  3. There are no units included with the hypotheses because variance does not have any units.
  4. The p-value is the area in the right tail of the [latex]\chi^2[/latex]-distribution, to the right of [latex]\chi^2=32.84[/latex].  In the calculation of the p-value:
    • The function is chisq.dist.rt because we are finding the area in the right tail of a [latex]\chi^2[/latex]-distribution.
    • Field 1 is the value of [latex]\chi^2[/latex].
    • Field 2 is the degrees of freedom.
  5. The p-value of 0.2992 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the variance of the scores on the final exam is most likely 25.

EXAMPLE

With individual lines at its various windows, a post office finds that the standard deviation for normally distributed waiting times for customers is 7.2 minutes. The post office experiments with a single, main waiting line and finds that for a random sample of 25 customers the waiting times for customers have a standard deviation of 4.5 minutes.  At the 5% significance level, determine if the single line changed the variation among the wait times for customers.

Solution:

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \sigma^2=51.84  \\ H_a: & & \sigma^2 \neq 51.84 \end{eqnarray*}[/latex]

p-value: 

From the question, we have [latex]n=25[/latex], [latex]s^2=20.25[/latex], and [latex]\alpha=0.05[/latex].

Because the alternative hypothesis is a [latex]\neq[/latex], the p-value is the sum of the areas in the tails of the [latex]\chi^2[/latex]-distribution.

This is a chi square distribution curve. The points chi square L and chi square R are on the horizontal axis. A vertical line extends from point chi square R to the curve with the area to the right of this vertical line shaded and labeled as one half of the p-value. A vertical line extends from chi square L to the curve with the area to the left of this vertical line shaded and labeled as one half of the p-value. The p-value equals the sum of area of these two shaded regions.

We need to calculate out the [latex]\chi^2[/latex]-score and the degrees of freedom:

[latex]\begin{eqnarray*} \chi^2 & = &\frac{(n-1) \times s^2}{\sigma^2} \\ & = & \frac{(25-1) \times 20.25}{51.84} \\ & = & 9.375 \\ \\ df & = & n-1 \\ & = & 25-1 \\ & = & 24 \end{eqnarray*}[/latex]

Because this is a two-tailed test, we need to know which tail (left or right) we have the [latex]\chi^2[/latex]-score for so that we can use the correct Excel function.  If [latex]\chi^2 \gt df-2[/latex], the [latex]\chi^2[/latex]-score corresponds to the right tail.  If the [latex]\chi^2 \lt df-2[/latex], the [latex]\chi^2[/latex]-score corresponds to the left tail.  In this case, [latex]\chi^2=9.375 \lt 22=df-2[/latex], so the [latex]\chi^2[/latex]-score corresponds to the left tail.  We need to use chisq.dist to find the area in the left tail.

Function  chisq.dist Answer
Field 1 9.375 0.0033
Field 2 24

So the area in the left tail is 0.0033, which means that [latex]\frac{1}{2}[/latex](p-value)=0.0033.  This is also the area in the right tail, so

p-value=[latex]0.0033+0.0033=0.0066[/latex]

Conclusion:

Because p-value[latex]=0.0066 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that the variation among the wait times for customers has changed.

NOTES

  1. The null hypothesis [latex]\sigma^2=51.84[/latex] is the claim that the variance in the wait times is 51.84.  Note that we were given the standard deviation ([latex]\sigma=7.2[/latex]) in the question.  But this is a test on variance, so we must write the hypotheses in terms of the variance [latex]\sigma^2=7.2^2=51.84[/latex].
  2. The alternative hypothesis [latex]\sigma^2 \neq 51.84[/latex] is the claim that the variance in the wait times has changed from 51.84.
  3. There are no units included with the hypotheses because variance does not have any units.
  4. In a two-tailed hypothesis test for population variance, we will only have sample information relating to one of the two tails.  We must determine which of the tails the sample information belongs to, and then calculate out the area in that tail.  The area in each tail represents exactly half of the p-value, so the p-value is the sum of the areas in the two tails.
    • If [latex]\chi^2 \lt df-2[/latex], the sample information belongs to the left tail.
      • We use chisq.dist to find the area in the left tail.  The area in the right tail equals the area in the left tail, so we can find the p-value by adding the output from this function to itself.
    • If [latex]\chi^2 \gt df-2[/latex], the sample information belongs to the right tail.
      • We use chisq.dist.rt to find the area in the right tail.  The area in the left tail equals the area in the right tail, so we can find the p-value by adding the output from this function to itself.
  5. The p-value of 0.0066 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the variance in the wait times has most likely changed.

TRY IT

A scuba instructor wants to record the collective depths each of his students dives during their checkout.  He is interested in how the depths vary, even though everyone should have been at the same depth.  He believes the standard deviation of the depths is 1.2 meters.  But his assistant thinks the standard deviation is less than 1.2 meters.  The instructor wants to test this claim.  The scuba instructor uses his most recent class of 20 students as a sample and finds that the standard deviation of the depths is 0.85 meters.  At the 1% significance level, test if the variability in the depths of the student scuba divers is less than claimed.

 

Click to see Solution

 

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \sigma^2=1.44  \\ H_a: & & \sigma^2 \lt 1.44  \end{eqnarray*}[/latex]

p-value: 

From the question, we have [latex]n=20[/latex], [latex]s^2=0.7225[/latex], and [latex]\alpha=0.01[/latex].

Because the alternative hypothesis is a [latex]\lt[/latex], the p-value is the area in the left tail of the [latex]\chi^2[/latex]-distribution.

This is a chi square distribution curve. The point chi square is on the horizontal axis. A vertical line extends from chi square to the curve with the area to the left of this vertical line shaded and labeled as the p-value.

To use the chisq.dist function, we need to calculate out the [latex]\chi^2[/latex]-score and the degrees of freedom:

[latex]\begin{eqnarray*} \chi^2 & = &\frac{(n-1) \times s^2}{\sigma^2} \\ & = & \frac{(20-1) \times 0.7225}{1.44} \\ & = & 9.5329... \\ \\ df & = & n-1 \\ & = & 20-1 \\ & = & 19 \end{eqnarray*}[/latex]

Function  chisq.dist Answer
Field 1 9.5329… 0.0365
Field 2 19
Field 3 true

So the p-value[latex]=0.0365[/latex].

Conclusion:

Because p-value[latex]=0.0365 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the variation in the depths of the students is less than claimed.

Watch this video: Hypothesis Tests for One Population Variance by jbstatistics [8:51]

Concept Review

To construct a confidence interval or conduct a hypothesis test on a population variance, we use the sampling distribution of [latex]\displaystyle{\frac{(n-1) \times s^2}{\sigma^2}}[/latex], which follows a [latex]\chi^2[/latex]-distribution with [latex]n-1[/latex] degrees of freedom.

The hypothesis test for a population variance is a well established process:

  1. Write down the null and alternative hypotheses in terms of the population variance [latex]\sigma^2[/latex].
  2. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
  3. Collect the sample information for the test and identify the significance level.
  4. Find the p-value (the area in the corresponding tail) for the test using the [latex]\chi^2[/latex]-distribution where [latex]\displaystyle{\chi^2=\frac{(n-1) \times s^2}{\sigma^2}}[/latex] and [latex]df=n-1[/latex].
  5. Compare the p-value to the significance level and state the outcome of the test.
  6. Write down a concluding sentence specific to the context of the question.
The general form of a confidence interval for an unknown population variance [latex]\sigma^2[/latex] is

[latex]\begin{eqnarray*} \mbox{Lower Limit} & = & \frac{(n-1) \times s^2}{\chi^2_R} \\ \\ \mbox{Upper Limit} & = & \frac{(n-1) \times s^2}{\chi^2_L} \end{eqnarray*}[/latex]

where [latex]\chi^2_L[/latex] is the [latex]\chi^2[/latex]-score so that the area in the left-tail of of the [latex]\chi^2[/latex]-distribution is [latex]\displaystyle{\frac{1-C}{2}}[/latex],  [latex]\chi^2_R[/latex] is the [latex]\chi^2[/latex]-score so that the area in the right-tail of of the [latex]\chi^2[/latex]-distribution is [latex]\displaystyle{\frac{1-C}{2}}[/latex] and the [latex]\chi^2[/latex]-distribution has [latex]n-1[/latex] degrees of freedom.

Attribution

“11.6 Test of a Single Variance“ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.