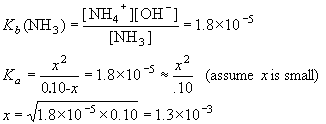14 Acid Base Chemistry
Michael Mombourquette
14.1: Introduction
In discussing equilibrium chemical systems, we must consider as one of the most important of these topics reactions involving acids and bases. Most acid-base systems are equilibrium ones. Let’s look at this field of chemistry, starting with some descriptive chemistry.
Acids and bases are relative terms. A molecule cannot be called an acid in exclusion of all else. For example, the gaseous hydrogen chloride molecule HCl(g) is a very stable molecule and does not act as acid or base unless something else is introduced to the system. If water is introduced to the system, the HCl readily reacts with the water to form H3O+(aq) and Cl–(aq). In other words, in the process of dissolving into the water, the HCl molecule gives up a proton to become Cl–(aq) and a water molecule accepts the proton and becomes H3O+(aq).
Arrhenius first defined an acid as a substance that gave protons when it dissolved in water and a base was something that gave the hydroxide ion when it dissolved in water. This definition, though, is rather restrictive and excludes a few substances that clearly are acids and/or bases.
According to the Brønsted-Lowrey definition, an acid is a molecule or ion that can easily give up (donate) a proton in a reaction with a base. Similarly, a base is a molecule or ion that can bond with (accept) a proton released by an acid in a reaction. This definition is broader than the Arrhenius definiton. In the reaction between hydrogen chloride (HCl) and water, the HCl is the acid and the water is a base. In the reaction between ammonia (NH3) and water, the water donates a proton to the ammonia molecule to make NH4+(aq) and OH–(aq). Thus, in this reaction, the ammonia is a base and the water is an acid. We have seen water as a Brønsted-Lowrey acid and as a Brønsted-Lowrey base. Water is amphiprotic.
We have experiences of acids and bases in our every day life, some of which we may not have recognized as being due to acid base properties. Take the following observations for example.
| Acids | Bases |
| Taste sour, eg., Vinegar (acetic acid and lemon (citric acid) | Taste bitter |
| Changes indicators’ colours | Also changes indicator colours (opposite change) |
| Reacts with carbonates (CaCO3), bubbles and releases CO2. | Reacts with organic matter (Caustic) |
| Reacts with most metals to dissolve the metal and release H2 gas. Ironically, this is an oxidation/reduction (REDOX) reaction, not an acid base reaction. M(s) + 2 HCl(aq) → MCl2(aq) + H2(g) |
Will react with aluminum to dissolve it, creating a solution of aluminum tetrahydroxide complex ions. 2Al(s) + 2NaOH(aq) + 6H2O(l) → 2Na+ + 2[Al(OH)4]– + 3H2(g). This is actually two reactions, an acid/base and a REDOX reaction. |
Acid properties are due to the hydrogen ion H+, more properly named the hydronium ion (H3O+).
When we represent an acid in reaction, we often use a shortcut HA (or HB) where the H is the proton that is released in reaction with bases and the A (or B) is the rest of the species.
The part, A or B may be neutral or may be charged. The part, without the H is the conjugate base of the form with the H.
| HB{ | HCl: the B is the chloride ion Cl– |
| HNO3: B is NO3– | |
| NH4+ : B is the NH3 molecule. |
A reaction between an acid and water can be represented as follows:
HB + H2O ![]() H3O+ + B–
H3O+ + B–
This representation of an acid-base reaction is a proton transfer reaction. This is the definition of acid/base systems called Brønsted-Lowrey. The double arrow is here because the vast majority of acid/water reactions reach equilibrium; they do not go to completion. The acid, HB, gives up a proton (H+) to become B– while the base (water) accepts the proton to become H3O+. Often, we ignore the water and simply write:
HB ![]() H+ + B–.
H+ + B–.
It is important to remember in this short-hand system that B, the “rest of the species”, is not necessarily negatively charged. The representation here merely indicates that the B part is relatively negative, compared to the HB. Take for example the acid/base system
NH4+ ![]() H+ + NH3.
H+ + NH3.
Here, B (NH3) is neutral but HA (NH4+) is +1 charged.
Our discussions in this course will be restricted to aqueous (water) solutions. In aqueous solutions, water plays a special role in that it can react with both an acid (as a base) and with a base (as an acid). Water is amphiprotic. When we dissolve any acid (or base) with water, there will be a reaction. The amount of reaction with water, depends on the strength of the acid.
HCl (g) + H2O (l) → H3O+ (aq) + Cl– (aq) Complete reaction (100%)
HF (aq) + H2O (l) ![]() H3O+ (aq) + F– (aq) not complete reaction (equilibrium)
H3O+ (aq) + F– (aq) not complete reaction (equilibrium)
Hydrogen chloride is a strong acid in water. That means it reacts with water completely. On the other hand, Hydrogen fluoride doesn’t react completely with water. It sets up an equilibrium with water. Some HF remains in solution undissociated. HF is a weak acid in water.
NOTE: the terms strong and weak apply only to an acid (or a base) reacting with water. If an acid reacts with a different base (not the conjugate base and not water), it will always react 100%.
An acid is formed when a compound has a hydrogen bonded to an atom that is moderately stable as a negative ion after the hydrogen ion is stripped off by a base. Inorganic acids generally are formed when hydrogens are attached to electronegative species like a halogen or complex ions like sulfates, which can exist as negative ions Organic molecules can have acidic properties. The most common type of organic acid is a carboxylic acid, as we see in the acetic acid molecule.
CH3COOH (aq) + H2O (l) ⇄ H3O+ + CH3COO– (aq)
The carboxylic acid portion of the molecule is a carbon with two oxygens attached with a hydrogen on one of them. This structure (see below) can form a stable anion because of resonance that occurs between the two oxygens after the hydrogen leaves.
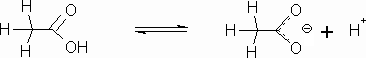
Acetic acid is also a weak acid. The hydrogen on the oxygen is the acidic hydrogen. It leaves behind a carboxylate ion (called the acetate ion in this case).
Actually, the vast majority of acids are weak acids. It would do you well to memorize the few acids that are strong and then you will always know that any other acid you encounter is a weak one.
The strong acids are:
- Hydrogen Halides (except HF), HCl, HBr, HI,
- Nitric acid, HNO3
- Sulphuric Acid H2SO4 (in dilute solutions only)
- Perchloric acid HClO4.
- Chloric acid HClO3
Bases are proton acceptors according to the Brønsted-Lowry definition. We’ve seen that water can act as a base
HCl (g) + H2O (l) → H3O+ (aq) + Cl– (aq)
Ammonia is also a base
HCl (aq) + NH3 (aq) → NH4+ (aq) + Cl– (aq)
Actually, since HCl is a strong acid, it is not really a good representation of reality to show the HCl reacting with another solute in water. Since HCl dissociates (according to the previous reaction) 100% in water, we never actually have HCl (aq) existing as a species. We have instead, H3O+ in the solution and it reacts with the ammonia
H3O+ + NH3 (aq) → H2O (l) + NH4+ (aq).
We can also have water acting as an acid.
H2O (l) + NH3 (aq) ⇄ OH– (aq) + NH4+.
Note that whereas the former reaction shows a 100% reaction this latter reaction is that of a weak base with water. Hence, an equilibrium is set up.
Alcohols can also act as an acid
R-O-H + :B– → R-O– + HB
The anion RO– is called the alcoxide ion (analogous to the hydroxide ion)
Like acids, The vast majority of bases are weak bases. The few strong bases include the alkali-metal hydroxides (NaOH, etc. and the oxide ion O2-).
Brønsted-Lowry bases all react with water to produce the hydroxide ion (OH–).
Brønsted-Lowry acids all react with water to produce the hydronium ion (H3O+).
Lewis Acids:
Lewis gave a different definition of acids which involved the transfer of electron pairs, rather than the transfer of protons. The two are compatible in that all Brønsted-Lowry acids are also Lewis acids but some Lewis acids are not Brønsted-Lowry acids. The Lewis definition is more general than that of Brønsted-Lowry.
Lewis acids are electron pair acceptors [like a proton accepts an electron pair when it bonds with a base]
Lewis bases are electron pair donors. [like the electron pair on the oxygen of a hydroxide ion is shared into the empty 1s orbital on the hydrogen cation (proton)]
Consider BF3 + F– → BF4–. the fluoride has lone-pair electrons which it shares into the empty orbital on the boron to form a new covalent bond. Hence, the fluoride is the electron pair donor (Lewis base) and the boron tri-fluoride is the electron pair acceptor (Lewis acid). No protons were transferred in this reaction so this is not a Brønsted-Lowry acid base reaction.
14.2: Acid-Base Neutralization Reactions
Consider
NaOH (aq) + HCl (aq) → NaCl (aq) + H2O (l)
Or
KOH (aq) + HBr (aq) → KBr (aq) + H2O (l)
Base + acid → Salt + water.
In all cases, the net ionic reaction is simply
H+ + OH– → H2O
The simplest type of chemical calculation involving acid-base reactions is a titration situation where the acid and base are exactly neutralized, i.e., they are both completely used up.
Example: A sample containing 25.00 mL of a NaOH solution was neutralized by 32.72 mL of a 0.129 M HCl solution. What was the concentration of the original sodium hydroxide solution.
First, write a balanced chemical equation
NaOH + HCl → NaCl + H2O
Now, use the concentration and volume of the HCL solution to find out how much HCL was added. We know that the HCL is all used up because the word “neutralized” implies that both the NaOH and the HCL are exactly used up.
![]()
We know that for perfect neutralization, all acid and base are exactly used up. The stoichiometry of this particular reaction shows a 1:1 ratio of acid and base, Therefore, the number of moles of acid added is equal to the number of moles of base in the original solution. Or, another way of saying this is:
![]()
Finally, the question asked for concentration of the initial NaOH solution. So we divide the number of moles of NaOH by the initial volume of the NaOH that was used.
![]()
This can all be accomplished in a single step using the extended fraction formalism as follows:
![]()
Note that there were two conversion factors (1000 mL/ 1L) and (1 L/ 1000 mL) that occurred in the individual calculations but which I ignored in the extended fraction formalism because they cancelled out. Also note that the ratio of NaOH to HCl does not need the units moles since they too cancel out.
14.2.1: Conjugate Acid-Base Pairs
The shorthand for an acid dissociation is HB ![]() H+ + B–. In this system, we see that an equilibrium exists. On the left-hand side, the acid HB dissociates (in water). On the right-hand side, the base B reacts with H+ to reproduce HB. We call this pair of acid and base a conjugate pair since they are interconverted by exchange of a proton.
H+ + B–. In this system, we see that an equilibrium exists. On the left-hand side, the acid HB dissociates (in water). On the right-hand side, the base B reacts with H+ to reproduce HB. We call this pair of acid and base a conjugate pair since they are interconverted by exchange of a proton.
Some examples of conjugate acid-base pairs are:
- HB
 H+ + B–
H+ + B– - HCl
 H+ + Cl–
H+ + Cl– - H2O
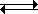 H+ + OH–
H+ + OH– - NH4+
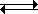 H+ + NH3
H+ + NH3 - H3O+
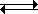 H+ + H2O
H+ + H2O - Acid
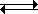 H+ + Base (conjugate pair)
H+ + Base (conjugate pair)
Similarly
- B + H+
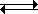 BH+
BH+ - H2O + H+
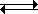 H3O+
H3O+ - CH3COO– + H+
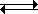 CH3COOH
CH3COOH - F– + H+
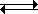 HF
HF - Base + H+
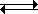 Acid (Conjugate pair)
Acid (Conjugate pair)
Every Acid-base reaction actually involves two acid-base conjugate pairs
| HA | + | B | A– | + | HB+ | |
| HF | + | H2O | F– | + | H3O+ | |
| H2O | + | CN– | OH– | + | HCN | |
| H2O | + | NH3 | OH– | + | NH4+ | |
| Acid 1 | Base 2 | Base 1 | Acid 2 |
Acid 1 and Base 1 are a conjugate pair.
Acid 2 and Base 2 are a conjugate pair.
Notice that water is both an acid and a base. It can donate a proton and it can accept a proton. It is called amphiprotic. We’ll see this later when we discuss the self-ionization of water.
14.3: Strength of Acids and Bases
We already saw that HCl is a strong acid in water. That means that it dissociates 100% when dissolved in water. This carries two implications. First of all, we never find a species called HCl (aq) actually existing in water since it is instantly dissociated to its ions. Second, If we look at the conjugate base of HCl (Cl–), we can immediately say that in any aqueous solution that contains the chloride ion, Cl– will never react to form HCl. Thus, even though Cl– is termed the conjugate “base” of HCl. It doesn’t in fact act as a base. We call this a very weak base. A strong acid has a very weak base as its conjugate.
Consider the weak acid HF. If we dissolve some HF in water, some of it will dissociate to form the conjugate base F–. However, if we dissolve some F– (say, NaF, dissolved in water) we know that some of the fluoride will set up an equilibrium to form some HF. Thus, a weak acid has a weak base as it’s conjugate.
Similarly, if we have a strong base (say, O2-) we know that if we have a solution containing OH–, it will never react as an acid to form the oxide ion. Thus, a strong base has a very weak acid as its conjugate.
| Acid | Base |
| Strong | Very weak |
| Weak | Weak |
| Very weak | strong |
Let’s reconsider the strong acid HCl. It cannot exist in aqueous solution. Neither can any strong acid. They all react with water to form H3O+. H3O+ is the strongest acid that can actually exist in aqueous solution. All stronger acids are levelled to H3O+.
Similarly, Strong bases are levelled to the strongest base that can exist in water, OH–. Thus, any intrinsic differences in the strengths of strong acids (or bases) are not detectable in water since they can’t exist in aqueous solution. We would need another solvent system to be able to distinguish the differences experimentally. For example, liquid sulfuric acid can be used as a solvent in which hydrochloric acid and all other ‘strong’ acids do not fully ionize. In other words, HCl is a weak acid when dissolved in H2SO4(l). To keep our discussions as simple as possible, our discussions of strong and weak acids and bases will generally be restricted to aqueous solutions, unless otherwise specified.
14.4: Equilibria in Acid-Base Systems
Consider the following reaction: HCl + H2O ![]() H3O+ + Cl–
H3O+ + Cl–
If we were to write an equilibrium constant expression for this reaction, we might at first attempt to create the following expression.
![]()
Recall that we write concentration here but actually an equilibrium constant is properly written using relative activities. Relative activities are written as:
![]()
In the case of the solute chemicals, standard concentration is 1 mol L-1. Hence, we can use Molar concentrations directly in the equilibrium equations by simply dropping the units. However, the standard concentration of a pure liquid is its normal molar concentration (in the case of water at 25℃, 55.5 mol L-1). If we’re considering dilute aqueous solutions, we can easily assume that the concentration of the water (solvent) is almost identical to the pure water concentration. Hence, it is a reasonably good approximation to assume that the relative activity of the solvent in a dilute solution is 1.
Thus, we don’t write the activities of solvents in the equilibrium expressions since they have no effect on the final value of K.
Our equilibrium for the reaction would thus be
![]()
The subscript a refers to the reaction type. Specifically, this K value refers to a reaction where one mole of acid reacts with water.
Example: What is the concentration of the species in a solution made up of 0.010 mol of HCl in 250 mL of water? Since at these concentrations, HCL is a strong acid, i.e., all the HCL is used up, we do a limiting reagent calculation. (“IF” table). Initial concentration of HCL is
![]()
| Balanced equation | HCl | + H2O → | H3O+ | + Cl– | |
| Initial concentrations (I) | 0.040 M | solvent, activity=1 | 0 | 0 | |
| Limiting Reagent=HCl: | all HCL used up, use storchiometry to get final concentrations. | ||||
| Final Concentrations (F) | 0 | 0.040 M | 0.040 M |
Thus, [H+] = [Cl–] = 0.04 M.
Obviously, we did extra work here in this example. We could have simply said that the reaction was complete and that the stoichiometry gives the final answers because of the one-to-one molar ratio. The IF table just helps some people visualize the process better. It is also useful as a precurser step in some ICE table calculations.
It’s not quite that simple if the acid (or base) is a weak acid.
For example, Consider the following.
HF + H2O ![]() H3O+ + F–
H3O+ + F–
![]()
The subscript a merely indicates that the equilibrium is that of an acid reacting with water. Please don’t think that there is anything else special about this relationship. In general, we can write an expression for any acid HB.
![]()
Example: What is the concentration of H3O+ in a 0.20 M solution of acetic acid?
[Ka (CH3COOH) = 1.8 ×10-5]
| CH3COOH | + | H2O | H3O+ | + | CH3COO– | ||
| I | 0.20 | 0 | 0 | ||||
| C | -x | +x | +x | ||||
| E | 0.20-x | x | x |
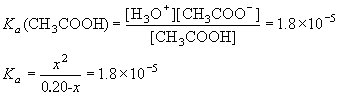
Obviously, this is a quadratic equation (it has a term in x2 and in x). In this case, there are two options we can use in order to solve this problem
1) Use the Quadratic formula
![]()
First, convert the Ka expression into the familiar quadratic form
![]()
| Note here that x is [H+], b is Ka and c is Ca×Ka. where Ca is the initial concentration of acid. We’ll use these notations in the “Summary of Calculation Types” section later. |
after some algebra:
x = 1.9×10-3M
2) Since the molar concentration of the acid is more than 100 times its equilibrium constant we can be fairly sure in making the assumption that the amount of reaction (x) is very small.
Assume 0.20 – x ~ 0.20. We can now rewrite the equilibrium constant expression by replacing the denominator as follows
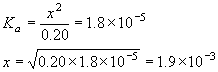
| Note here that this equation is easily generalizes as [H+] =(Ca×Ka)½ where Ca is the initial concentration of acid. We’ll use these notations in the “Summary of Calculation Types” section later. |
We should always check our assumptions.
0.20 × 0.0019 = 0.1982 (rounds to two sig figs) ~ 0.20. (no change) Actually, we might see a small change in the last digit. The limit for this type of assumption to be considered valid is 5%.
![]()
Thus, our assumption was good. We can normally consider that the assumption will be valid if
Ca > 100×Ka
or, in a problem where we add a base to water,
Cb > 100×Kb.
For concentrations we meet regularly here in first-year chemistry, that means if the K constant is about 10-5 or less, then the assumption will probably be good.
Example: What is [H3O+] in 0.20 M HCN? Ka = 4.9×10-10.
| HCN | + | H2O | H3O+ | + | CN– | ||
| I | 0.20 | 0 | 0 | ||||
| C | -x | +x | +x | ||||
| E | 0.20-x | x | x |
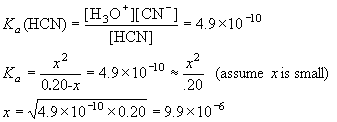
Thus, [H3O+] = [CN–] = 9.9×10-6 M.
To convert from activities back to concentrations in mol/L, just put the units on at the end since we dropped them when we converted to activities so we could insert the numbers into the equilibrium expression.
The percent ionization is
![]()
(This means that out of 100,000 molecules, only 5 are ionized when they dissolve in water at the specified overall concentration)
We can do all the same things for a weak base.
B + H2O ![]() BH+ + OH–
BH+ + OH–
![]()
Subscript b merely means that this equilibrium constant expression is for one mole of base (B) reacting with water.
Example: What is [OH-] in 0.10 M NH3? Kb (NH3)= 1.8×10-5.
| NH3 | + | H2O | NH4+ | + | OH- | ||
| I | 0.10 | 0 | 0 | ||||
| C | -x | +x | +x | ||||
| E | 0.10-x | x | x |
Thus, [NH4+] = [OH–] = 1.3×10-3 M.
| Note here that this equation is easily generalizes as [OH–] =(Cb×Kb)½ where Cb is the initial concentration of base. We’ll use these notations in the “Summary of Calculation Types” section later. |
The percent ionization is
![]()
In this case, our assumption is good. The amount of reaction x is less than 5% of 0.10.
14.5: Self-Ionization of Water
We’ve seen that water can act as both an acid and a base. In fact, water can be simultaneously the acid and the base in a reaction called the self-ionization of water.
H2O (l) + H2O (l) ![]() H3O+ (aq) + OH– (aq)
H3O+ (aq) + OH– (aq)
One water molecule gives up a proton to another water forming one hydronium and one hydroxide ion. This is also called the autoprotolysis of water. The equilibrium constant for this reaction would be:
KW = [H3O+] [OH–]
For pure water, the concentrations of the two ions are the same and are both 1.0 × 10-7. Hence,
KW = (1.0 × 10-7)2 = 1.0 × 10-14 @ 25℃
This equilibrium exists even in solutions of acids and bases and is the reason that there is always some H3O+ and some OH– ions present in solution even in strong acid and strong base solutions. Take for example, a solution of 0.010 M HCl.
HCl → H+ + Cl–
In solution, 0.010 M HCl will break up immediately and completely to 0.010 M H+ and 0.010 M Cl–. We’ll ignore the Cl– since it doesn’t contribute to the acid-base system at all.
Now, in the self-ionization of water, we set up initial and final conditions.
| H2O | + | H2O | H3O+ | + | OH– | |||
| I | 1 | 0,010* | 0 | *Due to the HCL | ||||
| C | +x | +x | ||||||
| E | 1 | 0.010+x | x |
Now, we can fill this into the equation for KW.
KW = (0.010+x)(x) = 1.0×10-14.
To simplify this calculation and avoid the quadratic formula, we’ll assume that the amount of reaction x was very small. Hence, we can replace 0.010+x by ~0.010.
KW = 0.010(x) = 1.0×10-14.
x = 1.0×10-12.
[OH–] = 1.0×10-12 M. So even in an acid solution, there is some hydroxide, albeit a very small amount.
Obviously, x is indeed very much smaller than 0.01 so the assumption is valid.
14.6: pH Scale
In water solution we can easily find H3O+ and OH– concentrations in the range between 1 and 10-15. For reasons of convenience and other scientific reasons, concentrations are often expressed on a logarithmic scale. For this, the ‘p’ function is used. It was first proposed by Sørenson. (S1909) You will see this function used in numerous ways in Science. Don’t get confused into thinking that each time you see it it is something new. In general
p X = -log X.
Whatever X is. In this case, we use pH and pOH to measure concentrations. Hence,
pH = -log [H+] and pOH = -log [OH–]
We already know that in aqueous solution KW = [H+][OH–] = 1.0×10-14. Because of a law in mathematics that says
log (x×y) = log x + log y
we can write
pKw = p([H+][OH–]) = pH + pOH = 14
We can also convert pH and pOH values back to [H+] and [OH–] values by using the inverse of the p function
[H+] = antilog(-pH) or [H+] = 10-pH
Let’s set up a table of pH and pOH values
| pH | [H+] | [OH–] | pOH | Examples |
| -1 | 10 | 10-15 | 15 | Conc. HCl {10 M, ca. 37% by wt} |
| 0 | 1 | 10-14 | 14 | |
| 1 | 10-1 | 10-13 | 13 | Stomach acid |
| 2 | 10-2 | 10-12 | 12 | “ |
| … | ||||
| 7 | 10-7 | 10-7 | 7 | Neutral (Pure water) |
| … | ||||
| 12 | 10-12 | 10-2 | 2 | Household ammonia |
| 13 | 10-13 | 10-1 | 1 | |
| 14 | 10-14 | 1 | 0 | 1 M NaOH solution |
| 15 | 10-15 | 10 | -1 | Drain Cleaner (extremely caustic) |
NOTES on pH (Theoretical definition):
pH has been more accurately defined as pH = -log aH+ where aH+ is the hydrogen ion activity. In solutions that contain other ions, activity and concentration are not the same. The activity is an effective concentration of hydrogen ions, rather than the true concentration; it accounts for the fact that other ions surrounding the hydrogen ions will shield them and affect their ability to participate in chemical reactions. These other ions effectively change the hydrogen ion concentration in any process that involves H+. In practice, Sørenson’s original definition can still be used, because the instrument used to make the measurement can be calibrated with solutions of known [H+], with the concentration of background ions carefully controlled.
The Experimental Definition:
IUPAC has endorsed a pH scale based on comparison with a standard buffer of known pH using electrochemical measurements. The IUPAC pH scale is very slightly different from the theoretical definition, since it considers factors that are not included in the (thermodynamic) theoretical pH.
Now let’s try some calculations,
What is the pH of a solution where:
a. [H3O+] = 1×10-3 M, b. [H3O+] = 5×10-3 M, c. [H3O+] = 1 M.
- pH = -log(1×10-3) = 3
- pH = -log(5×10-3) = 2.3
- pH = -log(1) = 0
That’s relatively simple, now let’s try some equilibrium calculations.
Example: What is the pH of a 0.20 M solution of acetic acid?
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & \mathrm{CH_3COOH} + & \mathrm{H_2O} & \rightleftarrows & \mathrm{H_3O^+} \;\;+ & \mathrm{CH_3COO^-} \\ \mathrm{Initial} & 0.20 & & & 0 & 0 \\ \mathrm{Change;\; x\; reacts} & -x & & & + x & + x \\ \mathrm{Equilibrium} & 0.20-x & & & x & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4c2923acc9135ff5d390954ab7a0ecb4_l3.png)
![]()
![]()
Assume 0.20 – x ~ 0.20. We can now rewrite the equilibrium constant expression by replacing the denominator as follows
![]()
![]()
We should always check our assumptions.
0.20 – 0.0019 = 0.1981 (rounds to two sig figs) ~ 0.20. (no change) Actually, we might see a small change in the last digit. Since the limit for an assumption to be considered valid is 5%.
![]()
Thus, [H+] = x = 1.9×10-3. Hence, pH = -log(1.9×10-3) = 2.72
Example: What is the pH of a solution of 25 mL of 0.20 M NaOH added to 40.0 mL of 0.15 M HCl?
Let’s first calculate the number of moles of each species.
25 mL NaOH × 0.20 mol/L = 5.0×10-3 mol NaOH (this is the limiting reagent)
40 mL HCl × 0.15 mol/L = 6.0×10-3 mol HCl (this is in excess)
Whenever we add an acid to a base, even a weak acid and a weak base, we react them with each other 100% (limiting reagent calculation) and then allow the excess react with water to find the final pH.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & \mathrm{HCl}\;\;\; + & \mathrm{NH_3} & \rightarrow & \mathrm{Cl^-}\;\;\; + & \mathrm{NH_4^+} \\ \mathrm{Initial} & 6.0\times 10^{-3} & 5.0 \times 10^{-3} & & 0 & 0 \\ \mathrm{Limiting\; reagent\; Ammonia}\\ \mathrm{Final} & 1.0 \times 10^{-3} & 0 & & 5.0\times 10^{-3} & 5.0\times 10^{-3} \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0771f9c4f899585e6dccc766e60d8a29_l3.png)
So now, we see that the HCl is excess, we allow it to react with water.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & \mathrm{HCl}\;\;\; + & \mathrm{H_2O} & \rightarrow & \mathrm{H_3O^+} \;\;\; + & \mathrm{Cl^-} \\ Initial & 1.0\times 10^{-3} & & & 0 & 5.0\times 10^{-3} \\ 100\% \; reaction \\ Final & 0 & & & 1.0\times 10^{-3} & 6.0\times 10^{-3} \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b73e3c0e5ba5f5dc4d8e0b63e7bc4c29_l3.png)
Notice that we were using moles here rather than activities. But, we were not doing equilibrium calculations (where we need activities) we were just doing simple stoichiometry calculations (100% reaction or limiting reagent). So, now that we have the final number of moles of H+, we can get the concentration by dividing by the new total volume.
#mol H+ = ![]() mol/L .
mol/L .
![]()
Hence, ![]() .
.
Examples:
Calculate the pH of the following solutions: a) 0.0100 M NaOH, b) 0.134 M NaOH
a. Since NaOH is a strong base,
![]()
![]()
![]()
![]()
Alternatively, we could have calculated ![]() first and converted to
first and converted to ![]()
![]()
![]()
b. now, with the 0.134 M NaOH solution
![]()
![]()
![]()
or calculate ![]() directly and then subtract from 14
directly and then subtract from 14
![]()
![]()
14.7: Distribution Diagrams
It is useful to look at a graphical technique of viewing acid-base equilibria. In this technique, we plot the relative amount of the components as a function of pH. Using this type of diagram, we can tell at a glance what the major constituents of a solution will be for any given pH (or pOH). The equations for creating these plots are found in the text book. We will not be expecting you to memorize them. However, those equations can be used to program an excel spreadsheet so that the plots can be created easily.
Let’s look at a distribution diagram for Acetic acid (![]() ).
).
CH3COOH (aq) → H+ + CH3COO– (aq)
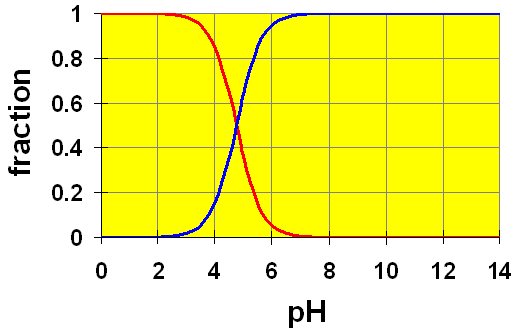
Here, we see two curves. These represent the concentrations of the acetic acid (red) and the acetate ion (blue). The Ka value of 1.8×10-5 gives a pKa = 4.74. You can see that in a solution of exactly pH=4.74, half of the original acetic acid would be ionized to acetate ion (and H+). At pH lower than 4.74, the proportion of acetic acid is larger and at pH higher than 4.74, more acetate ion is present.
Recall the example in the pH discussion above where we calculated the pH of a 0.20 M solution of acetic acid. We assumed that the amount of dissociation of acetic acid (x) was small compared to the initial amount. Once we had calculated the value for [H+] (and hence, the pH) we found that our assumption was true. The calculated pH was 2.72. Checking our chart, at a pH of 2.72 we can easily see that almost all of the original acetic acid is still present (relative amount ~ 1). Hence, by using this distribution chart, we can see visually that our assumption is good.
It is important to think of distribution diagrams in the correct terms. Remember, pH is the x axis. That means, this is a plot of how the acid-base system will behave in a solution of given pH. It is not usually used to tell us what pH a solution will attain by addition of some amount of acetic acid. For that, you need to do the calculations as we did above.
In yet another example, we looked at the equilibrium reached in 0.20 M HCN? Ka = 4.9×10−10. We calculated the value of [H+] to be 9.9×10−6 M. This gives a pH of 5. Let’s look at the distribution curve for HCN to see if pH 5 really does have mostly HCN present.
HCN + H2O ![]() CN− + H3O+
CN− + H3O+
Since ![]() , we see that the cross-over point (where [HCN]=[CN−]) occurs there. The value
, we see that the cross-over point (where [HCN]=[CN−]) occurs there. The value ![]() is well below the region where any significant dissociation of HCN occurs. Hence, it is safe to approximate the amount of HCN in solution as equal to the initial amount (to an accuracy of a few digits, anyway).
is well below the region where any significant dissociation of HCN occurs. Hence, it is safe to approximate the amount of HCN in solution as equal to the initial amount (to an accuracy of a few digits, anyway).
14.8: Relationship Between Ka and Kb for Conjugate Acid/Base Pairs
Consider the reaction between the weak acid HF and water.
HF (aq) + H2O ![]() H3O+ (aq) + F− (aq).
H3O+ (aq) + F− (aq).
HF and F− are conjugate acid and base respectively. We could say HF is the conjugate acid of F− or equally well, we could say that F− is the conjugate base of HF.
The ![]() can be written as:
can be written as:
![]()
We could also have written the equilibrium as that of the weak base F− reacting with water along with the expression for ![]() .
.
F− (aq) + H2O ![]() HF (aq) + OH− (aq).
HF (aq) + OH− (aq).
![]()
Now, if we add the two chemical equations together, we get the reaction for the self-ionization of water.
2 H2O ![]() H3O+ (aq) + OH− (aq).
H3O+ (aq) + OH− (aq).
Thus, the equilibrium constant KW can be represented as
![]()
![]()
Or
![]()
Or
![]()
This is a general relation, good for any conjugate weak acid/base pair.
It is possible to use the p function on the K values just as we did for pH and pOH. Thus, we can write
![]()
where the ![]() and the
and the ![]() refer to a conjugate acid/base pair.
refer to a conjugate acid/base pair.
Example: What is the base dissociation constant for the F− ion? Given Ka = 3.5×10−4.
Since HF and F− are a conjugate pair, we can write
Ka (HF) × Kb (F−) = 1.0×10−14
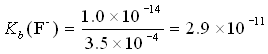
What if we had been given a value for pKa rather than Ka? Say, pKa = 3.46.
We could convert pKa to Ka and then use the relationship above. Or, easier, we convert pKa to pKb and then to Kb.
pKa(HF) + pKb(F−) = 14
pKb(F−) = 14 − 3.46 = 10.54
Kb = antilog(−10.54) = 10−10.54 = 2.9×10−11.
Notice that the reverse of function p (−log X = Y) is written according to mathematical principals as p−1
[X = antilog(−Y) or X = 10−Y].
14.9: Buffer Solutions
In many chemical processes, both industrial and biological reactions can only take place in a narrow range of [H3O+] concentrations (narrow pH range). To ensure that the desired reactions take place, buffers are used which hold the pH constant (within limits).
Examples of such chemical processes are:
- Sewage treatment: Bacteria only survive in a narrow pH range
- Photographic developing
- Electroplating
- Most metabolic processes
- Stomach pH ~ 1.5
- Saliva pH ~ 6.8
- Blood pH ~ 7.4
Buffers are used to maintain pH at some desired range. A Buffer is made up of approximately equimolar amounts of a weak acid and its conjugate base. To make these solutions, we could, for example add a weak acid (like Acetic acid) and the salt of the acid (like Sodium acetate) in equal proportions.
Video demonstration of the Buffer effect:buffer demo
Let’s consider the solution made up of CH3COOH and CH3COO− in approximately equal amounts.
CH3COO− + H3O+ ![]() CH3COOH + H2O
CH3COOH + H2O
According to La Châtelier’s principal If we add a small amount of acid, the acetate ion will react with it and reduce the effective change in pH. If we add a small amount of base, the acetic acid will react with it and again reduce the effective change in pH. The amount of acid and base added must be smaller than the amount of buffer or it will simply use up all the buffer and then proceed to change the pH.
To restate what we said in more mathematical terms:
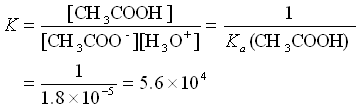
Here, we see that the equilibrium constant for the reaction of the acetate ion with acid is very large. Hence, any acid added to the buffer solution will be immediately used up in the buffer equilibrium. Similarly, the K for the reaction of the acetic acid with a base is large and the base will be used up.
Buffer Example: What is the pH of a solution of 0.050 mol acetic acid and 0.050 mol of acetate ion in 1 L of solution?
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & CH_3COOH\;\;\; + & H_2O & \rightleftarrows & CH_3COO^-\;\;\; + &H_3O^+ \\ \mathrm{Initial} & 0.050 & & & 0.050 & 0 \\ \mathrm{Change x reacts} & -x & & & + x & + x \\ \mathrm{Equilibrium} & 0.050-x & & & .050+x & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d67513346469906415382e5a2257fac0_l3.png)
Here, we assume that x is small and that we can replace 0.050+x by 0.050 and 0.050-x by 0.050.
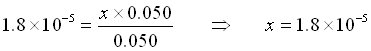
(Yes, x is small compared to 0.050)
![]()
![]()
NOW, let’s add 0.001 mol HCl to the solution (Pretend no volume change just for simplicity in this example).
The HCl will react immediately with the acetate to use 0.001 mole of acetate and produce the same amount of acetic acid.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & \mathrm{CH_3COOH}\;\;\; + & \mathrm{H_2O} & \rightleftarrows & \mathrm{CH_3COO^-}\;\;\; + &\mathrm{H_3O^+} \\ \mathrm{Initial} & 0.051 & & & 0.049 & 0 \\ \mathrm{Change x reacts} & -x & & & + x & + x \\ \mathrm{Equilibrium} & 0.051-x & & & .049+x & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3763b549752586fe44db5d764c0aef31_l3.png)
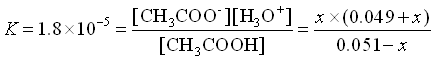
Again, we assume that x is small.
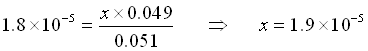
(Yes, x is small compared to 0.049)
![]()
![]()
We see in the above example, that the pH has changed from 4.74 to 4.72, a very small change, considering that if we had added the HCl to 1 L of pure water, the resulting pH would have been 3.
What if we had added .01 mol HCl rather than .001 mol. That’s ten times as much.
Our initial values would have changed by 0.01 rather than by 0.001.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & CH_3COOH\;\;\; + & H_2O & \rightleftarrows & CH_3COO^-\;\;\; + &H_3O^+ \\ \mathrm{Initial} & 0.060 & & & 0.040 & 0 \\ \mathrm{Change x reacts} & -x & & & + x & + x \\ \mathrm{Equilibrium} & 0.060-x & & & .040+x & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d9853bd972a753995d9a39cdfd7131c9_l3.png)
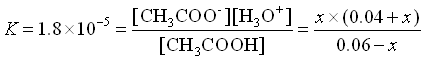
Again, we assume that x is small.
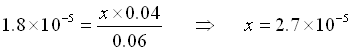
(Yes, x is small compared to 0.050)
![]()
![]()
Even adding 0.01 mol of HCl only changed the pH by about .16 units. Had we added the HCl to pure water, the pH would have changed from 7 to 2 (5 units). Thus, the buffer was effective in holding the pH steady.
Let’s look at the distribution diagram for acetic acid/acetate again to see this effect visually.
CH3COOH (aq) ![]() H+ + CH3COO− (aq)
H+ + CH3COO− (aq)
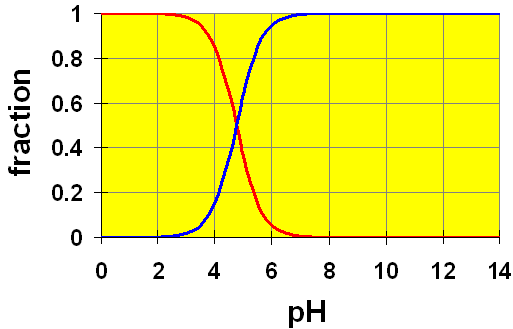
The initial pH of the buffer solution, before adding the HCl was 4.74. This is exactly the cross-over point on the graph where the relative amounts (concentrations) of the acetate and the acetic acid are equal. Notice that at this point, the slope of the curves is very steep. This means that to make any change in pH, we must make large changes in the relative amounts of the acid and conjugate base. Note too that this range extends from just below pH=4 to pH=6. A pH range of about 2 or a relative concentration range of 100. Thus, we can have a buffer solution of any weak acid/conjugate base system as long as the ratio of the acid to the base is between about 10 and 0.1.
Buffer Example: What is the pH of a solution of 1.00 mol of NH3 and 0.40 mol of NH4Cl in 1.0 L of solution? Is this a buffer solution?
NOTE: NH4Cl is a salt that dissolves completely to form ammonium ion and chloride ion.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} & \mathrm{NH_3}\;\;\; + & \mathrm{H_2O} & \rightleftarrows & \mathrm{NH_4^+}\;\;\; + &\mathrm{OH^-} \\ \mathrm{Initial} & 1.00 & & & 0.40 & 0 \\ \mathrm{Change:\; x\; reacts} & -x & & & + x & + x \\ \mathrm{Equilibrium} & 1.00-x & & & .040+x & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f30e4cba8ef72eace8652f5badca3a75_l3.png)
![]()
assume x is small:
![]()
Hence,
![]()
![]()
![]()
To see if this is a buffer, we can look at the ratio of acid to base:
![]()
This ratio is well within the range 10 to .1 so it is a buffer solution.
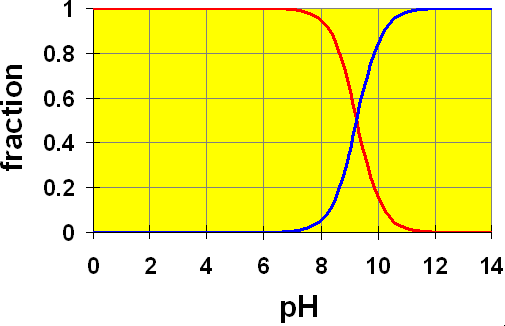
Looking at the distribution diagram for ammonia (pKb = 4.74 so pKa = 9.26) we can also see that pH = 9.66 is in the buffer zone (slope of the line is steep).
NH3 + H2O ![]() NH4+ + OH–
NH4+ + OH–
We can derive a general equation to deal with calculations of pH of buffer solutions.
HA + H2O ![]() A– + H3O+
A– + H3O+
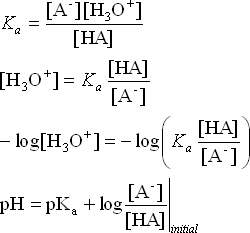
We are using initial concentrations because if we are truly in a buffer zone the amount of change in the relative concentrations of the acid and conjugate base is small.
This equation is called the Henderson-Hasselbalch equation. And it is a very useful shortcut to calculating the pH of a buffer solution once we have established the initial concentrations like we did in the examples above.
We see that the primary contribution to the pH of a buffer solution is the pKa of the acid/base pair. And modifications to the pH are affected by adjusting the relative concentrations of the acid and base. Thus, by carefully choosing the correct acid/base pair, we can create a buffer of any pH we wish.
A buffer is most effective at resisting change in pH when [base] = [acid]
pH = pKa + log(1) = pKa.
A one-to-one molar ratio is not always desired. What if we need to achieve a specific pH value, not quite equal to pKa for the buffer system we are using?
Example: Blood has a pH of 7.4. and is buffered by a carbonic acid/hydrogen carbonate buffer system. What is the ratio of acid to base required to keep the pH at 7.4, given pKa(H2CO3) = 6.37
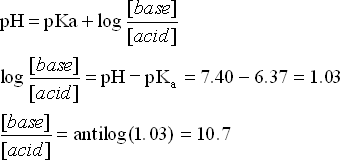
We need a ratio of 10.7 base to acid to maintain a pH of 7.4. This is right on the edge of the buffer region for the buffer system we used here. In reality, the buffer system used by our blood is much more complex system than we used here and so thankfully, we are not quite on the edge, so to speak.
Well, we’ve learned how to look at distribution diagrams and how to do equilibrium calculations. In this next section, we’ll review a bit of both and show more how these two ideas can be combined to help in the understanding of acid-base equilibria.
We’ve seen that for a monoprotic acid/base system (one proton is exchanged) the distribution diagram consists of two curves that cross at a value pH = pKa. (or pOH = pKb). We’ve also seen that the width of the curved space is about 2 pH units. This means that we can always draw a quick distribution diagram for any acid/base conjugate system knowing only the Ka (or pKa), or the Kb (pKb) of the weak acid or weak base respectively.
Let’s take for example, the acetic acid / acetate system.
We know that Ka (HAc) = 1.8×10-5. So pKa = -log(1.8×10-5) = 4.74. Thus, we can quickly draw a distribution diagram by drawing a rectangle to represent the plot area. The axes are:
- Y: fraction, range = 0 to 1.
- X: pH, range= 0 to 14.
The cross-over of the two curves occurs at about 4.7 and the width of the cross-over area is 1 pH unit to either side of 4.7 (about 3.7 to 5.7). The resulting sketch of the distribution diagram is shown below.
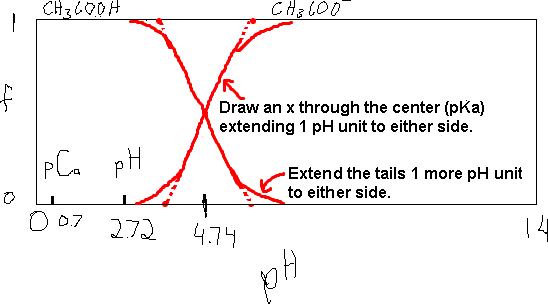
Here, we see the cross-over at 4.74 and we know the width of the area is 2 units (NOTE). Our drawing doesn’t have to be perfect. The information is still there.
Excel spreadsheet to calculate distribution curves. Distribution_Curves
14.10: Summary of Calculation Types
When we have a problem involving adding a weak acid or base to water, we can sometimes make simplifying assumptions in our calculations. The ICE table process for acid/base calculations will always lead us to a quadratic equation and so we can always simply plow through the work of using the full quadratic solution to get to our desired answer. In many circumstances, however, we can simplify the calculations by assuming certain variables are insignificant and therefore can be ignored. When can we make such assumptions? It turns out that the decision as to when we can make the assumptions are based both on the concentration of the acid (or base) involved and on the strength (Ka or Kb value) of the starting material.
We’ll do the math here for acid added to water but the same can be done for base added to water by substituting the appropriate variables Cb, Kb and pOH, as needed.
Case 1: Ca >> Ka : the final pH is located to the left of the buffer region in the weak acid region.
Now, lets look again at the acetic acid example we did above. In that example, we asked for the pH of a 0.20 M solution of acetic acid. After some work and the assumption that x was small, we worked out that [H+] = (CaKa)1/2 = 1.9×10-3. And therefore that pH = 2.72.
So, by making the assumption x << Ca, we were able to avoid using the quadratic equation and shorten the amount of work we needed to do. We can use the equation we get out of the ICE table in two forms, depending on what final answer we need.
If we need the [H+] then the algebraic form as follows is quicker:
![]()
If we need the pH for our answer then the logarithmic form is quicker.
![]()
or, rearranged:
![]()
In words, the ![]() is the average of the
is the average of the ![]() and
and ![]() .
.
This is easily visualized in the diagram where the ![]() and
and ![]() are indicated.
are indicated. ![]() is half-way between
is half-way between ![]() and
and ![]() . Obviously, if the halfway point between the
. Obviously, if the halfway point between the ![]() and
and ![]() lies within the buffer zone then all bets are off as far as simplifying assumptions.
lies within the buffer zone then all bets are off as far as simplifying assumptions.
We could do the same in the case of a solution of weak base where the ![]() is half-way between
is half-way between ![]() and
and ![]() .
.
![]()
Example: We can determine the pOH of a solution of 0.30 M ammonia as follows
![]()
![]()
The pH can easily be calculated to be
![]() .
.
In both of these cases, the concentration C is larger than K by a factor of at least 100. C < 100 × K. This is called the concentrated limit. In the case where the concentration is not so high (100K > Ca > .1K), the assumption that the reaction is small is not valid and we must use the quadratic formula.
Case 2: Ca within two orders of magnitude. Ka: final pH will lie in the buffer region.
Take acetic acid again, if Ca were to be, say, .0002 we would find that the amount of dissociation is no longer negligible (x is not small) and we would need to use the quadratic formula. After rearranging the resulting Ka expression at equilibrium to fit the quadratic expression 0 = ax2 + bx + c, we determine that x = [H+] , a = 1, b = Ka and c = -KaCa. Thus,
![]()
![]()
![]()
Notice that in this last example, the amount of dissociation (0.00007) is a sizable fraction of the initial amount (0.0002)
0.00007/0.0002×100% = 35%, definitely not negligible. If we look at the distribution curve diagram for acetic acid, we see that at a pH of ![]() is in the buffer region; the slope of the distribution curve in the buffer region (Near pKa) is very steep and hence, we cannot make any assumptions.
is in the buffer region; the slope of the distribution curve in the buffer region (Near pKa) is very steep and hence, we cannot make any assumptions.
Case 3: Ca << Ka : to the right of the buffer region, in the strong-acid region.
In an extremely dilute weak acid, we can always assume that the acid dissociates 100% just like a strong acid. The amount of dilution necessary to allow for 100% ionization is called the strong acid limit. The strong acid limit occurs at the edge of the buffer region (~Ka/10). Thus, any acid whose concentration Ca is less than about Ka/10 is in the strong acid region.
In the strong acid region, even weak acids behave like strong acids so the assumption, CH+ = Ca and pH = pCa is a reasonable approximation unless Ca is less than or equal to about 1×10-7. In this case, we must include considerations of self-ionization of water in any calculations.
For example, a concentration of acetic acid of Ca = 1×10-6 is in the strong acid region for acetic acid. So, all the acetic acid will dissociate, resulting in a pH = 6. If we use an acetic acid solution with Ca = 1×10-8 M , the final solution would still be in the strong-acid region for acetic acid but the pH would not go higher than about 7, since water alone will contribute 1×10-7 M of H+ and hence the additional small amount of H+ from the acetic acid will only slightly change that. Another way of thinking of it… we cannot get a pH of 8 (basic solution) by adding a small amount of acid to water.
We summarize the shortcuts we’ve just discussed in the following table. The table is given for weak acid added to water and so the subscripts are all a and we calculate [H+] and pH.
| Conc. | Range of conc. | p-function equivalent | Equations |
| High | Ca > 100Ka | pCa< pKa – 2 | [H+] = (KaCa)1/2 pH = (pKa + pCa)/2 |
| Medium | 100K > Ca > 0.1K | pKa – 2 < pCa< pKa + 1 | |
| Low | 0.1K > Ca | pKa + 1 < pCa | [H+] ~ Ca pH ~ pCa |
The equations for weak base added to water can all be derived by changing all references for acid into references for base, i.e.,
[H+] ==> [OH–], pH ==> pOH, Ca ==> Cb and Ka ==> Kb. Additionally, when looking at the distribution diagrams, we swap left and right references, i.e., the weak base region is right of the buffer region and the strong base region is left of the buffer region.
14.11: Acid-Base Properties of Salts
In an earlier part of this section on acid-base reactions, we said that the reaction between an acid and a base results in a salt and water. The questions arises, Is this solution neutral? In other words, are the products neutral? Is the Salt Neutral?
To know the answer, we can look at the acid/base properties of the two ions that make up the salt. If we don’t know their properties offhand, we can sometimes figure out the answer by checking the conjugates of the ions. There are four possible cases:
14.11.1: Salt of Strong Acid and Strong Base
Consider an example, hydrochloric acid and sodium hydroxide. If they are added together in aqueous solution such that they exactly neutralize each other, the result will be a NaCl solution in water.
HCl + NaOH → NaCl + H2O
In this case, the solution is the result of the neutralization of a strong acid with a strong base and the pH is exactly 7. In other words, the salt NaCl is neither acidic nor basic. The Na+ is a very weak acid (the conjugate acid of a strong base, NaOH), in other words, it is not an acid. The Cl– ion is a very weak base (the conjugate base of a strong acid, HCl), and is therefore not a base. So NaCl is a salt made up of a cation that is not an acid and an anion that is not a base. It is neutral.
Such is not the case if the original acid and base are not both strong.
14.11.2: Salt of Strong Acid and Weak Base
Take, for example, the reaction between Hydrochloric acid and ammonia, a weak base.
HCl + NH3 → NH4Cl
Here, we still have the anion Cl– that we know to be not a base. the cation, NH4+, however is a weak acid. It’s the conjugate acid of the weak base NH3, since the conjugate of a weak base is always a weak acid. Thus, the salt ammonium chloride is made up of a cation ammonium which is a weak acid and an anion Cl– that is not a base. Thus, the solution of ammonium chloride is acidic.
14.11.3: Salt of Weak Acid and Strong Base
What about a solution of sodium acetate, NaCH3COO? Is it acidic or basic?
The cation is Na+ is obviously neutral, as we discussed for case 1. The anion is acetate CH3COO–, the conjugate base of the weak acid acetic acid CH3COOH. Since acetic acid is weak, acetate is also weak. So, sodium acetate is made up of a neutral cation and a basic anion. This solution is basic.
14.11.4: Salt of Weak Acid and Weak Base
Now for the hard one. What if both the anion and the cation are non-neutral?
Take, for example a salt ammonium acetate, NH4CH3COO. Is it acidic or basic?
We’ve seen that the ammonium ion NH4+ is acidic and the acetate ion CH3COO– is basic. The answer to the questions lies in a comparison of the relative strengths of the acidic cation and the basic anion. The stronger one wins. In other words, if Ka > Kb the solution will be acidic. If Ka < Kb then the solution is basic. It turns out, that in this case, the two happen to be almost equal (to about 2 sig. figs) so the salt sodium acetate is almost neutral.
We now have a way of determining the acid-base properties of any salt solution. In each of these cases, we could have said that the stronger ion wins, in the first three cases, at least one of the ions was very weak and we could easily discard it. In the fourth case both ions were weak and we had to compare directly the two to determine the answer.
What if you were asked to calculate the pH of a salt solution. In the first three cases above, the calculations are relatively simple.
In case 1, the pH is 7. That’s simple.
What is the pH of a 0.1 M solution of sodium cyanide?
We know that the sodium ion is a very weak acid (i.e., not an acid) and we will not consider it further. It’s a spectator ion. The cyanide ion CN–, however is the conjugate of the weak acid hydrogen cyanide HCN and is a weak base. We do the calculation of a weak base in water.
| CN– | + H2O | HCN + | OH– | ||
| I | 0.1 | 0 | 0 | ||
| C | –x | +x | +x | ||
| E | 0.1-x | x | x |
![]()
![]()
In this case, Cb > 100Kb so we can assume x is small. We can do the ICE table calculation or jump to the shortcut.
![]()
![]()
14.12: Polyprotic Acids
So far, in our discussion of acids and bases, we have focused on acids that donate only one proton (and bases that accept only one). Acids of this type are called monoprotic acids. Some acids can have more than one proton to donate. The general class of these is called polyprotic acids.
Polyprotic acids can be categorized according to how many protons they donate:
- Diprotic acids donate two protons. Examples include H2SO4, H2SO3, H2CO3 and (COOH)2
- Triprotic acids donate three protons. An example of this class of acids is H3PO4
In the case of strong acids, we can merely consider that the ratio of acid to base in a stoichiometric calculation is not 1:1, for example, in dilute solutions H2SO4 can be considered to be a strong acid. And especially in a reaction with a base, we can write,
H2SO4 (aq) + 2 B ![]() SO42- + 2 HB+.
SO42- + 2 HB+.
Here we can plainly see that the ratio of acid to base is 1:2, not 1:1 as would be the case if a monoprotic acid had reacted with the same base.
If the acid is not a strong acid, then we must consider the equilibria that occur in the solution.
The generalized reaction scheme for reaction of a diprotic acid with water can be written as follows. We take the protons off the acid one at a time and set up an equilibrium for each step.
- H2B + H2O
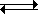 H3O+ + HB–
H3O+ + HB–
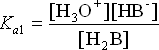
2. HB– + H2O ![]() H3O+ + B2-
H3O+ + B2-
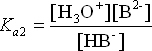
These two equilibria exist simultaneously in the solution. This multiple equilibrium scenario is not easy to work with calculation-wise. Under certain circumstances, we can make some simplifying assumptions in our calculations. There are three different sets of conditions we should consider.
- The Ka values are separated by at least 4 orders of magnitude (pKa values are separated by at least 4). In this case, we can consider the equilibria separate from each other. One does not affect the other. It allows for certain assumptions to be made in the calculations.
- The Ka values are less than 4 but greater than 1 order(s) of magnitude apart (1< ΔpKa < 4) we are in an intermediate area where the equilibrium of step 1 is never completely separated from that of step 2 but where some separation is still visible.
- The Ka values are only one order of magnitude apart (1 pH unit separation of pKa values). In this case, it is nearly impossible to distinguish the two equilibria using experimental techniques. Calculations can still determine the amounts of all reactants.
Lets look at the distribution diagrams for cases like these. ( Distribution curves)
Case 1: pKa separation is 5.
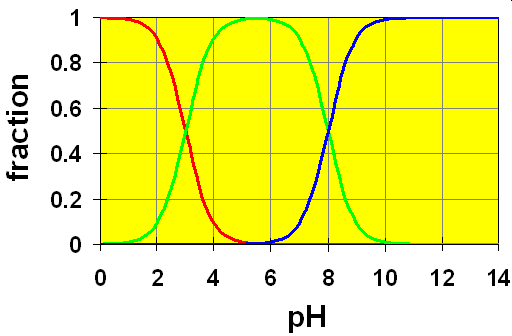
Here, the curves are colour coded: Red represents H2B, Green is HB– and Blue is B2-. We see that the red-green crossover area is completely separated from the green-blue crossover area. This means that the acid H2B is completely converted to HB– before any significant amount of HB– dissociates to form B2-.
Case 2: pKa separation is 2:
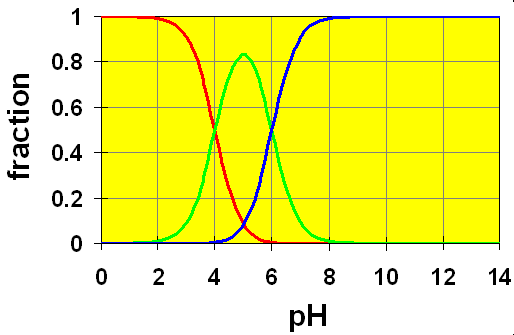
Here, we wee that the green curve never completely reaches mole fraction of 1. In this case, the second equilibrium takes effect and uses up the HB–. In the intermediate region between two crossover points, significant concentrations of all three species H2B, HB– and B2- are present simultaneously. Obviously, calculations in this region will not be as simple as in case 1.
Case 3: pKa separation is .5
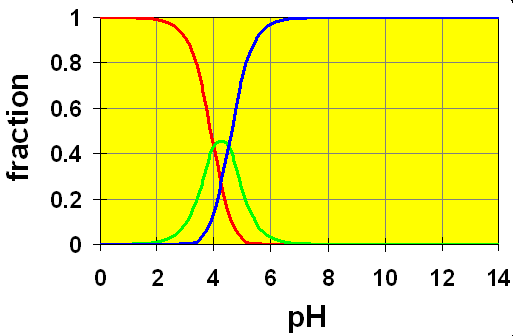
Here, we see that the amount of HB– is always quite low and experimentally, it would be very hard to distinguish the two different equilibria. We have what looks like a distorted crossing zone between the red and blue curves with the green poking through as a slight perturbation on the curves. We might think of the HB– as an intermediate species whose concentration doesn’t build up very much. In these cases, except under extremely carefully controlled pH situations, the reaction of H2B with a base occurs in “nearly” a single step.
Let’s look at some calculations involving the triprotic Phosphoric acid, H3PO4.
We will look at each equilibrium in turn:
- H3PO4 (aq) + H2O
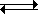 H3O+ (aq) + H2PO4– (aq)
H3O+ (aq) + H2PO4– (aq)
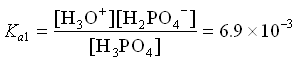
2. H2PO4– (aq) + H2O ![]() H3O+ (aq) + HPO42- (aq)
H3O+ (aq) + HPO42- (aq)
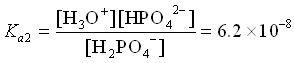
3. HPO42- (aq) + H2O ![]() H3O+ (aq) + PO43- (aq)
H3O+ (aq) + PO43- (aq)
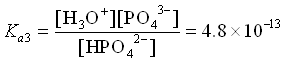
We see that the Ka values are all separated by about 5 orders of magnitude. That means that the equilibria can all be treated independently of each other, as in Case 1 above. We can see this even more clearly if we look at the distribution diagram for H3PO4.
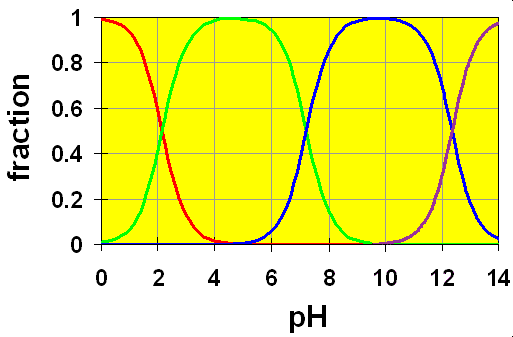
Here, the colored lines represent the following species:
- RED => H3PO4,
- GREEN => H2PO4–,
- BLUE => HPO42–,
- VIOLET => PO43–,
It is clear to see in the distribution diagram that the three crossover regions corresponding to the three Ka values are completely separate from each other.
Using the three Ka relationships, we can now calculate the concentration of all species involved in the equilibria.
Example: Calculate the concentration of H3PO4, H2PO4–, HPO42-, PO43- and H3O+ in a 0.100 M solution of H3PO4.
STEP 1: the first proton is removed.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccccc} First\; K_a\; value& H_3PO_4 & + & H_2O & \rightleftarrows & H^+& + & H_2PO_4^- \\ \mathrm{I } & 0.100 & & & & 0 & & 0 \\ \mathrm{C } & -x & & & & + x & & + x \\ \mathrm{E } & 0.100-x & & & & x & & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a6aaa2a3244acb24d8f8c42d60e8c05d_l3.png)
![]()
We cannot assume that x<<0.100 since Ca is less than 100×Ka. We must use the quadratic equation. (NOTE)
![]()
recall: ![]() . So, after some algebra, we find
. So, after some algebra, we find
![]() ≡ [H+] = [H2PO4–] (in mol L-1).
≡ [H+] = [H2PO4–] (in mol L-1).
[H3PO4] = 0.100 – 0.023 = 0.077 M
However, some of the H2PO4– will dissociate in the second equilibrium. Will it affect the concentration found here significantly? Probably not since the value of Ka2 is about 105 smaller than Ka1. Let’s do the calculation to prove it.
STEP 2: the second proton is removed.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccccc} Second\; K_a\; value& H_3PO_4&+ & H_2O & \rightleftarrows & H^+& + & H_2PO_4^- \\ \mathrm{I } & 0.023 & & & & 0.023 & & 0 \\ \mathrm{C } & -x & & & & + x & & + x \\ \mathrm{E } & 0.023-x & & & & 0.023+x & & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-98391d6c305abd85e17e36ec218dfaf4_l3.png)
![]()
This time, ![]() and we can assume the amount of H2PO4– that dissociates (a.k.a. x) is <<0.023.
and we can assume the amount of H2PO4– that dissociates (a.k.a. x) is <<0.023.
![]()
![]() ≡ [HPO42-] (in mol L-1)
≡ [HPO42-] (in mol L-1)
NOTE: our assumption that x is small is a good one this time (x is 6 orders of magnitude smaller than 0.023). That means that according to the ICE table the concentrations of H+ and of H2PO4– calculated in step 1 are not significantly changed in step 2.
Finally, in a like manner, we can use the third equilibrium to calculate the concentration of the PO43- using the initial concentrations we’ve calculated here for HPO42- and H+.
STEP 3: the third proton is removed.
![Rendered by QuickLaTeX.com \[\begin{array}{cccccccc} Third\; K_a\; value& H_3PO_4& + & H_2O & \rightleftarrows & H^+& + & H_2PO_4^- \\ \mathrm{I } & 6.2\times 10^{-8} & & & & 0.023 & & 0 \\ \mathrm{C } & -x & & & & + x & & + x \\ \mathrm{E } & 6.2\times 10^{-8}-x & & & & 0.023+x & & x \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5cb7189afd3b05d360af7a3bbceffff6_l3.png)
assume x is small again means we can simplify the calculations.
![]()
![]() ≡ [PO43-] (in mol L-1).
≡ [PO43-] (in mol L-1).
This time, our assumption that x is small is valid; x << 6.2×10-8 and x <<0.023. We see that the concentrations of H+ and HPO42- that we calculated in step 2 are not significantly affected by this (step 3) equilibrium.
We’ve now calculated the concentrations of all the species in the 0.100 M solution of H3PO4.
As the neighbouring Ka values get closer than about four orders of magnitude, We get increasingly erroneous results by assuming that the two equilibria are independent of each other (as we were able to do for H3PO4). We won’t delve into this further in this course. That’s for a future course in analytical chemistry.
We can still do some calculations, even in cases where Ka values are close.
In the distribution diagrams of polyprotic acids, there are several special points that we should consider. We’ll look at the distribution diagram for phthalic acid.
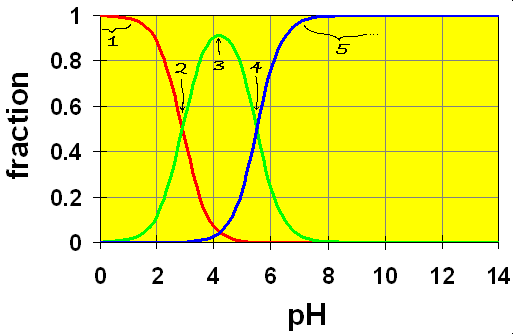
Here we see the crossover points representing the two equilibria (color coded)
(Dihydrogen phthalate or phthalic acid) H2P ![]() H+ + HP−; (hydrogen phthalate)
H+ + HP−; (hydrogen phthalate)
![]()
(hydrogen phthalate) HP– ![]() H+ + P2- (phthalate ion)
H+ + P2- (phthalate ion)
![]()
Note that you can purchase hydrogen phthalate in many hardware stores as KHP, Potassium Hydrogen Phthalate. It’s a base that is strong enough to help you wash off grease from the walls before you paint but not so strong as to wash off the skin from your hands. But use rubber gloves anyway.
First off, we see that the two equilibria overlap somewhat and there are three species present in solution. Now let’s look at the regions of this diagram try to understand them. (see numbers on diagram)
- Low pH range (
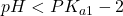 ). In this range, the ion H2P exists mostly undissociated, just as we would expect in a monoprotic acid.
). In this range, the ion H2P exists mostly undissociated, just as we would expect in a monoprotic acid. 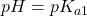 . At this point, the concentration of H2P and HP– are equal. We are in the centre of the first buffer region.
. At this point, the concentration of H2P and HP– are equal. We are in the centre of the first buffer region.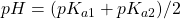 . The point half-way between the two crossover regions is where the solution can be considered to be made up of the HP– ion (and some H2P and P2-). This is the pH we would get if we made a solution by adding the salt of the HP– ion to water. A good exam question is to ask for the pH of a solution of the amphiprotic species. It’s a real simple calculation but some students won’t know this and will try using ice tables, to no avail.
. The point half-way between the two crossover regions is where the solution can be considered to be made up of the HP– ion (and some H2P and P2-). This is the pH we would get if we made a solution by adding the salt of the HP– ion to water. A good exam question is to ask for the pH of a solution of the amphiprotic species. It’s a real simple calculation but some students won’t know this and will try using ice tables, to no avail.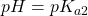 . At this point, the concentration of HP– and P2- are equal. This is the centre of the second buffer region.
. At this point, the concentration of HP– and P2- are equal. This is the centre of the second buffer region.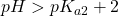 . In this region, both equilibria are completed and the solution is one of the pure base P2- in water.
. In this region, both equilibria are completed and the solution is one of the pure base P2- in water.
14.13: Titrations
Acid base Titrations are used to determine amounts (concentrations) of acids and bases in solutions of unknown composition. You performed a titration in your first lab where you determined the concentration of an unknown acid by reacting it with a carefully measured volume of standardized base (from the burette). Knowing the volume and concentration of the base, and the stoichiometry of the acid-base reaction involved, you were able to calculate the amount of acid in the reaction vessel (beaker) and hence, its concentration.
In an acid-base titration, the object is to measure exactly the amount of titrant it takes to react completely with the sample. This point, where the acid and base have exactly neutralized each other is called the equivalence point. Let’s explore the process of a titration so we can understand the system. Then, we can devise a method to experimentally determine equivalence points and perform the experiments.
For our first example we’ll be titrating 25 cm3 of a 0.10 M strong acid (in the beaker) with a 0.10 M strong base (in the burette). The discussion following is valid for any strong acid and any strong base. The titration curve depicted below will be identical in all cases.
Since both the strong acid and the strong base are 100% dissociated upon addition to water, we’ll not consider equilibria further.
- Thus, at the start, before any base (from the burette) is added to the beaker, the concentration of H+ = Ca; so
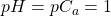 .
. - As base is added from the burette, the acid already in the beaker reacts with it and keeps the pH from rising. This is called the buffer region even though in this case, it’s not a true buffer since the pH is only protected in one direction. In this region, we can calculate [H+] directly by simply subtracting the number of moles of added base from original number of moles of acid and dividing by the new total volume.
![Rendered by QuickLaTeX.com \[\mathrm{[H^+]}=\frac{C_aV_a-C_bV_b}{V_a+V_b}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a6a795f464b7a1ea92541c895960aaf1_l3.png)
- When all the acid is used up, the pH rises rapidly with further addition of base. The steepest part of this rapid rising region occurs at the equivalence point. Since at this point, we have exactly used up the acid (and haven’t yet added extra base), we have only a salt solution. The pH of the equivalence point is therefore determined by the salt. In a strong-acid-strong-base reaction, the salt is exactly neutral and so the pH of the equivalence point is 7. This is not the case if weak acids or weak bases are involved.
- Beyond the equivalence point, the pH asymptotically approaches the value
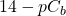 .
.
A strong base titrated with a strong acid would give a curve that is similar but upside-down compared to this one.
See if you can figure out the relationships for the four regions discussed in the acid/base case above.
If we titrate a weak acid with a strong base, the resulting titration curve depends on the Ka values for the acid being titrated. In this case, we must consider the equilibrium process at all times so the equations to determine the concentrations of H+ (and hence, ![]() ) are much more complicated. We’ve already explored all the equations we need here so there’s nothing new to learn.
) are much more complicated. We’ve already explored all the equations we need here so there’s nothing new to learn.
Let’s titrate 25 cm3 of 0.1 M acetic acid with 0.1 M KOH.
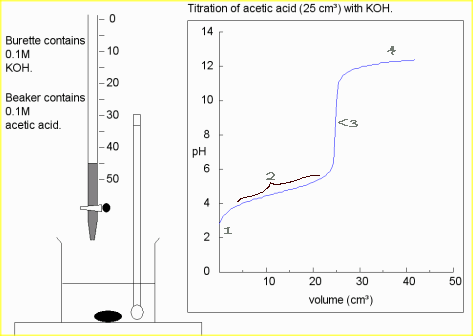
- At the start, the pH is simply that of a 0.1 M solution of acetic acid. Using the shortcut method we learned earlier (
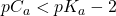 ) we have
) we have
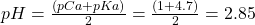 .
. - As base is added, the acetic acid is converted into acetate (base from the burette reacts 100% with the acid). This is a true buffer region, where there will be some acetic acid not yet reacted as well as some acetate ion that results from the reaction with the added base. The amount of acetic acid remaining (not counting the equilibrium) is simply
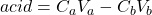 .
.
This is our initial amount of acid to be used in the “I” line of an ICE table calculation.
The amount of acetate is equal to the amount of base added is
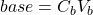 .
.
This is the initial amount of base to be used in the “I” line of the ICE table calculation.
As we saw in the two buffer example calculations above, when the Initial conditions include some acid and some conjugate base such that the pH is in the buffer region, we can always use the Henderson-Hasselbalch equation to calculate pH and skip the rest of the ICE table calc.
![]()
A special point along the buffer region occurs when the amount of base added is exactly half of the amount of acid we had originally. At that point, the concentration of the acetic acid is exactly equal to the concentration of the acetate and the Henderson-Hasselbalch equation reduces to ![]() .
.
This is called the half-titration point and exactly corresponds to the crossover point observed in the distribution diagram for acetic acid.
- At the equivalence point all the acetic acid has been converted to acetate. Hence, we simply have a solution of 0.050 M acetate (volume doubled because of added base). Hence, the
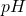 can be determined using standard methods for the solution of a weak base. Since 0.050 is definitely more than 100 times larger than
can be determined using standard methods for the solution of a weak base. Since 0.050 is definitely more than 100 times larger than 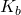 (acetate) we can use the shortcut again.
(acetate) we can use the shortcut again.
![Rendered by QuickLaTeX.com \[pOH = \frac{(pC_b + pK_b)}{2} = \frac{(1.30 + 9.24)}{2} = 5.27\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d6dbd6a4f43995b00ee9d2151930b22f_l3.png)
![Rendered by QuickLaTeX.com \[pH = 14 - pOH = 14 - 5.27 = 8.73.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2ffa4512fbc3eb82a2e1b151748642b0_l3.png)
- As we add more base, just as in the strong acid case, the
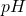 now only depends on the concentration of the base added and asymptotically approaches the value
now only depends on the concentration of the base added and asymptotically approaches the value 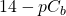 .
.
Now we determine a way to observe the titration experimentally. Several methods can be used to determine the equivalence point of an acid-base reaction. One method involves graphical analyses of the titration curve (![]() vs. volume added), where the equivalence point is the inflection point at the steepest part of the sharp uprising of the
vs. volume added), where the equivalence point is the inflection point at the steepest part of the sharp uprising of the ![]() with volume of base added (point 3 above). This is most accurately done using a computer that can take the second derivative of the titration curve to find the zero point. See the table below.
with volume of base added (point 3 above). This is most accurately done using a computer that can take the second derivative of the titration curve to find the zero point. See the table below.
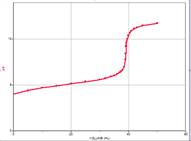 pH curve showing the equivalence point as the steepest slope. At this point, the acid is completely used up and the pH rises quickly from that of the acid to that of the base as more is added. pH curve showing the equivalence point as the steepest slope. At this point, the acid is completely used up and the pH rises quickly from that of the acid to that of the base as more is added.
If the Indicator you Choose has a pKa in this steep slope region then the color change will occur quite quickly as the pH rises. Usually, in less than one drop. Did yours? |
|
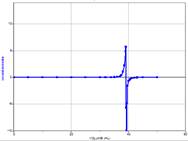 Second derivative of the pH curve. The point where the second derivative crosses zero is the equivalence point. This is a highly accurate way to measure the equivalence point of a solution, even in cases where the use of an indicator is not practical, such as in coloured or cloudy solutions. Second derivative of the pH curve. The point where the second derivative crosses zero is the equivalence point. This is a highly accurate way to measure the equivalence point of a solution, even in cases where the use of an indicator is not practical, such as in coloured or cloudy solutions. |
An other method, which does not require plotting pH versus volume is to add an indicator to the reaction mixture. This is an excellent low-tech method that can be very accurate in clear colourless solutions.
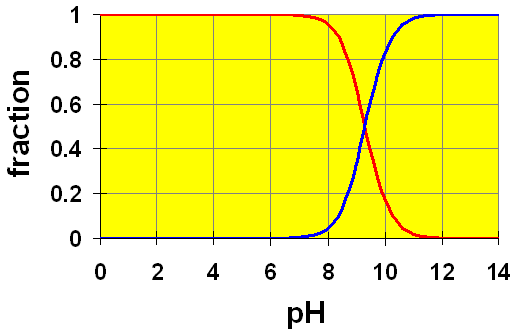
An indicator is a weak acid that is coloured and whose colour is different from that of its conjugate base (or vice versa). For example, the indicator phenolphthalein is colourless in acid solution but is pink in basic solution. We can see this if we look at the distribution diagram for phenolphthalein.

We see that the colourless species (light grey) exists primarily at pH values below about 8 and the pink species (red line) exists primarily at pH values above 10. In between, the colours are mixed and the colour change is in process. It may seem that indicators are not very accurate in that the pH has to shift over a pH range of 2 or so before the colour change can be seen. However, at the equivalence points of many acids, that is exactly what happens. Recall that while there is still some acid (and its conjugate base) in solution, the solution will be somewhat buffered against pH changes. Once the last of the acid (or conjugate base) is used up, there can be rapid pH changes with small additions of titrant from the burette. Hence, a rapid colour change occurs with as little as one drop of titrant past the equivalence point. This colour change is called the end point and if our indicator is chosen well, it will coincide closely with the equivalence point. If the indicator is poorly chosen, the two points will not match and any calculations based on the endpoint will be inaccurate. Thus, the pH range of this indicator is nearly the same as the equivalence point for acetic acid. Hence, phenolphthalein is a good indicator for the titration of acetic acid with a strong base.
Excel spreadsheet to calculate titration curves. Note that to view this file properly, it’s best to download it and run it in the desktop Excel rather than trying to use the on-line Excel.
Video: universal indicator