Kinetics

Michael Mombourquette

18 Kinetics

18.1: Introduction

In the previous thermodynamics chapters, we’ve studied mostly the difference between final and initial states (state function). There was no way for us to use thermodynamic information to tell us why some reactions, although spontaneous, will not proceed while others do. That is the job of Kinetics.

We’ve seen that some reactions are fast (even explosive) and others are quite slow (rusting of iron). In this section, we are going to study reaction kinetics and try to gain an understanding of how and why reaction rates are what they are. We will also look at how kinetics studies can help us to understand the mechanisms of reactions.

We will study the effect of concentration, temperature and catalysts on reaction rate. This type of information will allow us to understand details of chemistry which takes place during the reaction.

18.2: Reaction Rate

Rate $\Rightarrow$ speed

For a car, a speed is the distance traveled (change in position) divided by the time. For chemical reactions we define speed (Rate) as change in concentration divided by time. More specifically, we use either the concentration of a product or a reactant in our definition of RATE for a chemical reaction.

$RATE=\frac{amount\;of\;reaction}{reaction\;time}$

For a given chemical reaction, the amount of reaction is measured using the concentration changes of one measurable reactant or product and can be determined from the stoichiometry.

Consider: NO(g) + O₃(g) $\rightarrow$ NO₂(g) + O₂(g)

For every reaction we get one NO₂ so there is a 1:1 correspondence. Thus, the amount of reaction can be replaced by the change in concentration of NO₂.

If [NO₂] at t₁ is [NO₂]₁ and @t₂ is [NO₂]₂ then

Δ[NO₂] = [NO₂]₂ – [NO₂]₁

and

Δt = t₂ – t₁

and

rate = Δ[NO₂]/Δt

Since the rate is always positive and the forward reaction will produce NO₂, i.e., Δ[NO₂] is positive the signs are consistent. If we had used a reactant concentration, the signs would be reversed. If non unit number of moles of material are produced for one mole of reaction then we would need to consider that too.

For the above reaction we can write:

In the reaction: N₂(g) + 3 H₂(g) $\rightarrow$ 2NH₃(g)
we could write:

The factor of 1/3 for the H₂ comes into play, of course since the rate of consumption of H₂ is three times as fast as the rate of reaction. The factor of 1/2 for the NH₃ is there for the same reason, the rate of production of ammonia is equal to twice the rate of reaction since its coefficient is 2.

The above definition of rate involves a measurable time span Δt. Over this time, it is possible that the actual rate changes. In this case, the above equations are actually definitions of average rates over the time interval Δt. To get the instantaneous rate, we need to shrink the time interval down to an infinitesimally small span and thus the rate could now be written using dC/dt rather than ΔC/Δt.

To measure rates, we normally measure concentrations or something related to concentration.

There are several methods we might employ to do this measurement.

We can withdraw a small sample from the reaction mixture at various times, quench the reaction (maybe by cooling it rapidly) and then measuring the concentrations using whatever method is most convenient (like standard wet chemical methods).
If one species is coloured, we might do the reaction inside a cell in a spectrometer and measure the change in the absorption. Beer’s law says that the amount of absorption is proportional to the concentration.
For gas-phase reactions, we can measure pressures at constant volume.
And many others. Some new ones are being developed continuously.

Let’s look at an example reaction and consider the changes which occur as the reaction (time) progresses

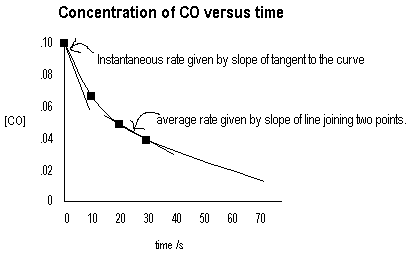
The reaction CO(g) + NO₂(g) $\rightarrow$ CO₂(g) + NO(g) is initiated and concentrations are measured at several times with the following results.

Time/s	[CO]	[NO₂]	Average Rate Δ[CO]/Δt	Instantaneous rate d[CO]/dt
0	0.100	0.100		0.0049
			0.0033

10	0.067	0.067		0.0022
			0.0017

20	0.050	0.050		0.0012
			0.0010

30	0.040	0.040

18.3: Rate Laws and Reaction Order

There is a connection between the kinetics and the chemistry which is actually occurring. In this section, we will begin to explore that connection and learn how to determine rate laws and reaction order from reaction kinetics.

Consider the reaction

NO(g) + O₃(g) $\rightarrow$ NO₂(g) + O₂(g) measured at 25°C.

Rate of reaction is found experimentally to be proportional to [NO] and to [O₃]. Therefore, we can write the equation:

$Rate = k \mathrm{[NO] [O_3]}$

where $k$ is the rate constant (a measure of the intrinsic rate). For this reaction at 25°C,

$k = 1.6\times 10^7\mathrm{ mol^{-1}s^{-1}}$

This reaction is first order with respect to NO and to O₃ and is second order overall

Some general information about rate constants and reaction order.

Fast reactions have large values of k

Slow reactions have small values of k.

In general, for a reaction

aA + bB + cC + … $\rightarrow$ products

Rate = k [A]^x [B]^y [C]^z ×…

Where x, y and z are the order of reaction of A, B, and C, respectively and are not necessarily related to coefficients a, b and c in the balanced chemical reaction. The overall reaction gives essentially, the initial and final states (reactants and products). The kinetics represent the process in between.

Consider the reaction

2 N₂O₅(g) $\rightarrow$ 4 NO₂(g) + O₂(g)

Experimental data collected and some calculated rates are tabulated here.

t/min	[N₂O₅]	Rate
0	.0172
10	.0113	3.4×10^-4
20	.0084	2.5×10^-4
30	.0062	1.8×10^-4
40	.0046	1.3×10^-4
50	.0035	1.0×10^-4
60	.0026	0.8×10^-4

If we plot [N₂O₅] versus time we find the following:

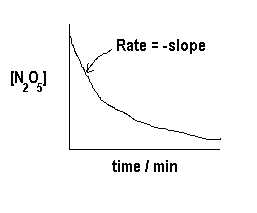
From this graph, we can calculate the rate (the -slope) at various times t (and at various concentrations of N₂O₅). Now we plot $rate$ versus [N₂O₅] to see if we get a straight line just like the straight-line equation

$Rate = k\mathrm{[N_2O_5]}$

.

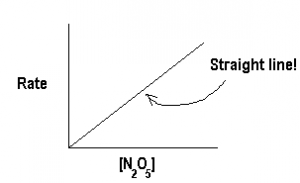
Since we do get a straight line, we know that rate is directly proportional to [N₂O₅], i.e., the order of reaction is 1.

We can double check this by plotting rate against other orders of [N₂O₅], for example lets try order=2.

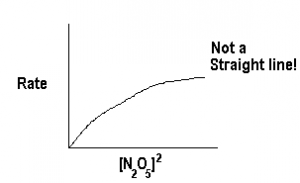
Obviously, Rate is not proportional to [N₂O₅]², i.e., $Rate \not= k\mathrm{[N_2O_5]^2}$ . Since we do not get a straight line for any other order, we can be assured that the reaction order is 1.

18.3.1: Initial Rate Method

Some reactions have more than one reactant. This complicates the issues since all concentrations are changing at once and we cannot use the above method to determine the reaction order with respect to any one reactant. In addition, sometimes the reverse reaction will complicate things by affecting the apparent rates. Both these problems can be alleviated using the initial rate method.

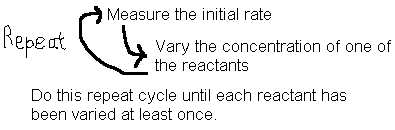
From the rate data collected, we can now see how rate is affected by changes in concentration of just one of the chemicals at a time and we have eliminated the reverse reaction in the process.

Example:

Experimental rate data was collected for the following reaction. Determine the rate law.

2 NO + Cl₂ $\rightarrow$ 2 NOCl

Expt.	[NO]	[Cl₂]	Initial rate
1	0.010	0.010	1.2×10^–4
2	0.010	0.020	2.3×10^–4
3	0.020	0.020	9.6×10^–4

The rate law will have the form $Rate = k \mathrm{[NO]^x [Cl_2]^y}.$

Our job is to determine $x$ and $y$ .

Let’s look at these reactions in pairs, specifically, pairs where the only difference is the concentration of just one reactant. 1,2 and 2,3 are such pairs.

Experiments	Observations	Conclusions
Experiments 1 and 2	[NO] $\rightarrow$ constant [Cl₂] $\rightarrow$ doubles Rate $\Rightarrow$ doubles	Rate proportional to [Cl₂] $y = 1$
Experiments 2 and 3	[Cl₂] $\rightarrow$ constant [NO] $\rightarrow$ doubles Rate $\Rightarrow$ quadruples	Rate proportional to [NO]² $x = 2$

Our rate law can now be written as

$Rate = k \mathrm{[NO]^2 [Cl_2]}$

The overall reaction order is 3, the order with respect to NO is 2 and wrt. Cl₂ is 1.

We’ll explore the meaning of this reaction order later in the section on reaction mechanisms.

The above example was done in a bit a of a hand-waving way here. If you wish to see a more mathematically rigorous derivation of the same rate law, see below.

Experimental rate data was collected for the following reaction. Determine the rate law.
2 NO + Cl₂ ® 2 NOCl

Expt.	[NO]	[Cl₂]	Initial rate
1	0.010	0.010	1.2×10^-4
2	0.010	0.020	2.3×10^-4
3	0.020	0.020	9.6×10^-4

The rate law will have the form Rate = k [NO]^x [Cl₂]^y.

We have an equation with three unknowns (k, x, and y); Rate is measured. We need at least three different measurements of Rate to be able to solve this problem.

$\begin{array}{ll} 1&1.2 \times10^{-4} = k \times 0.010^x \times 0.010^y\\ 2&2.3 \times10^{-4} = k \times 0.010^x \times 0.020^y\\ 3&9.6 \times10^{-4} = k \times 0.020^x \times 0.020^y \end{array}$

Now, we can solve for the three unknowns,

divide equations 2/1

$\begin{array}{rl} \frac{2.3\times 10^{-4}}{1.2\times 10^{-4}} &= \frac{k \times 0.010^x \times 0.020^y}{k \times 0.010^x \times 0.010^y}\\ \\ 1.9 \approx 2 &= 2^y\\ y &= 1 \end{array}$

Divide equations 3/2

$\begin{array}{rl} \frac{9.6 \times10^{-4}}{2.3\times 10^{-4}}&= \frac{k \times 0.020^x \times 0.020^y}{k \times 0.010^x \times 0.020^y}\\ \\ 4.1 \approx 4 &= 2^x\\ x &= 2$

We now know both $x$ and $y$ . We can solve for k using any one of the three equations.

$1.2\times 10^{-4} = k\times 0.010^2 \times 0.010^1 k = 1.2\times 10^2$

Example

What is the rate constant at 300K for the following reaction:

2 NO + Cl₂ $\rightarrow$ 2 NOCl ?

We already know the rate law is

Rate = k [NO]² [Cl₂]. We can use the values from any one of the experiments from the previous example. We’ll use expt. 1. (2 and 3 should also give the same value for k)

What is the rate of this reaction when [NO] = 0.030 M and [Cl₂] = 0.040 M?

$\begin{array}{rl} Rate&= k\mathrm{ [NO]^2 [Cl_2]}\\ &= 1.2\times10^2 \mathm{M^{-2}s^{-1}} \times (0.030)^2 \times (0.040)\\ &= 4.3\times10^{-3} \mathm{M^{-2}s^{-1}}. \end{array}$

18.3.2: Integrated Rate law method

We can determine the rate law by comparing slopes (conc. / t). From this graph, we can then determine the rate at any time t and then plot it versus concentration to various powers. From these powers, we determine the plot which is linear and hence, establish the order with respect to the reactant.

A more direct method, is to integrate the rate-law equations as they were previously expressed (slope of conc. versus time == derivative d[A]/dt) and from these integrated rate-law expressions, plot different functions of concentration versus time to see which one gives a straight line. In addition, the integrated rate laws help us to further our understanding of the concentration changes which occur and lead to a determination of the half-life of the reactant.

In all these examples, a single reactant species A is under consideration. For many reactions, we can set up conditions such that only one of the reactants need be considered at any time. We do this by starting the reaction with all species except one in very large excess. Hence, during the progression of the reaction, the change in concentrations of the large excess compounds will be very small. We can hence, set up a pseudo rate law. In other reactions, there is only one reactant to consider. Whichever the case, the following rate laws are not general and should not be taken to be the only possible forms.

Consider a first-order situation: A $\rightarrow$ products.

$Rate = \frac{-d\textrm{[A]}}{dt}= k_1\textrm{[A]}$

Integrating gives

$\textrm{ln}\frac{\textrm{[A]}_t}{\textrm{[A]}}=-k_t$

or

$\mathrm{ln[A]_t}} = -kt + \mathrm{ln[A]_0}$

taking the anti-log of both sides of this equation gives:

$\mathrm{[A]_t}=[A]_0}\; e^{-kt}$

In other words, the concentration of A falls off exponentially as is pictured here

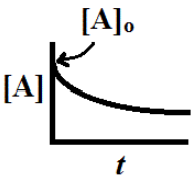
We can plot the ln [A]t versus t to give is a plot that should be a straight line plot with slope = -k.

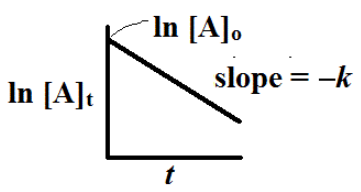
Now consider a second-order system.
A → products

$rate = k_2 \mathrm{[A]^2} = \frac{-d\textrm{[A]}}{dt}$

Integrating gives us

$\frac{1}{\mathrm{[A]_t}} = k_2t + \frac{1}{\mathrm{[A]_0}}$

If we plot 1/[A] versus t, we should get a straight-line plot with slope = k.

A more rare case: Zero-order reactions.

This type of rate law implies no dependence of rate on concentration. This mostly occurs when a catalyst is used with a large excess of reactant. In this type of situation, the rate is dependent solely on the total number of reactant sites available on the catalyst.

$Rate = \frac{-d\mathrm{[A]}}{dt} = k$

integrating gives

$\mathrm{[A]_t} = -kt + \mathrm{[A]_0}$

A plot of [A] versus t gives a straight line with slope = $-k$ .

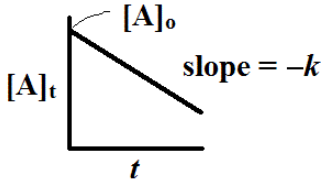
18.3.3: Half-life

The half-life of a chemical species is defined as the time necessary to reduce the concentration of the species to one half it’s initial value. In mathematical terms, at $t = t_{1/2}$

$\mathrm{[A]_t} = \frac{\mathrm{[A]_0}}{2}$

First-order reaction:

$ln \mathrm{[A]_t} = -kt + ln \mathrm{[A]_0}$

$ln\frac{\mathrm{[A]}_0}{\mathrm{[A]_t}}=kt$

$ln\frac{\mathrm{[A]}_0}{1/2\mathrm{[A]_0}}=kt_{1/2}$

$ln 2 = kt_{1/2}$

$t_{1/2} = \frac{ln 2}{k}= \frac{0.693}{k}$

Similarly, for second order, we get

$t_{1/2} = \frac{1}{k\textrm{[A]}_0}$

For the rare zero-order case, we find

$t_{1/2} = \frac{\textrm{[A]}_0}{2 k}$

Notice that for first-order reactions, $t_{1/2}$ does not change as you change [A]₀ but for second or zero order reactions, $t_{1/2}$ depends on the amount of A. Only in first order reactions is the half life constant.

Example:

The hydrolysis of sucrose to glucose and fructose is catalyzed by an enzyme sucrase. It is first order with respect to sucrose. If the half-life is measured to be 80 min. @ 25°C what proportion of the initial sucrose will remain after 160 and after 320 min?

First-order ==> Conc = 1/2 every 80 min. time interval.

160 min = 2 intervals of 80 min. so concentration halves twice.

$C = 1/2 [ 1/2 (C_0)] = 1/4 C_0$

One quarter of the sucrose will remain after 160 min.

320 min = 4 intervals of 80 min.

$C = (1/2)^4 \times C_0 = C_0/16$

One eighth of the initial amount of sucrose will remain after 320 min.

Another example

The half-life of N₂O₅ in the first-order decomposition @ 25°C is 4.03×10⁴s. What is the rate constant? What percentage of N₂O₅ will remain after one day?

1 day is 8.64×10⁴ s.

From the integrated rate law:

22.6 % remaining after one day.

18.4: Temperature and Reaction Rate

Since reactions involve both breaking bonds (needs energy) and reforming bonds (releases energy) there is almost always an amount of energy which must be input to the molecules before reaction can be initiated. We could represent this using an energy scale versus reaction coefficient as follows.

A theory called Collision Theory or Activated Complex Theory is often used to explain rates of reaction. Energy is most often transferred to the bonds which must be broken during (or as a result of) a collision. These collisions are most often the collisions between the reacting species themselves but could also be collisions with other non-reacting gas molecules and even with the wall of the container (a hot wall). We expect that only collisions with sufficient energy will initiate reaction. We see from this diagram of an exothermic reaction that a minimum energy to initiate the reaction is give by the value of the activation energy E_a. Hence, only collisions between reactant molecules with energy > E_a will result in products.

In the gas phase there are a large number of collisions which have sufficient activation energy but still do not react. This is due to the ‘steric’ factor. By this, we mean the molecules must collide with the correct relative orientation before a reaction will occur. This steric factor is not temperature dependent. There are other factors which also affect rate. In a large molecule, the energy of collision must be concentrated in the bond or bonds which must be broken. This may take time and is statistically determined. This too is not dependent on temperature.

If we look at an ensemble of gas molecules at a certain temperature, we will see a distribution of kinetic energies. This means there will be a distribution of kinetic-energies of colliding molecules. The energy of collision is related to the total kinetic energy of the colliding atoms and to the angle of incidence. Like a car, a head-on collision converts more kinetic energy into “collision” energy than does a glancing (sideswipe) collision. This is another kind of steric factor and is not dependent on temperature. Hence, the only factor which is really dependent on energy is the average kinetic energy of collision. If we plot frequency of collisions versus energy of collision, we see a distribution curve which changes as T changes.

We can see that the number of collisions which occur with a high enough energy (at least Ea) is less in the case of the low temperature curve (area under the curve) versus the high energy curve. Hence, as temperature goes up, we expect that reaction rate will go up.

Click Here for a spreadsheet that demonstrates this principle

18.4.1: Arrhenius Equation

Experimentally, it can be demonstrated that the temperature dependence of k can be expressed as follows:

$k = A e^{-E_a/RT}.$

This is known as the Arrhenius equation where the pre-exponential factor A contains information about the non-temperature-dependent items discussed above and Ea is the activation energy. We see that the rate constant (and therefore the rate) of a reaction will be lower for higher values of Ea and will increase as T increases.

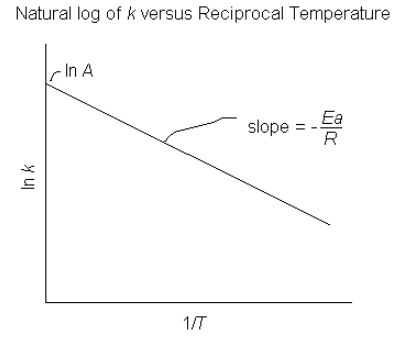
The Arrhenius equation can also be written in log form as follows

$ln\ k = ln\; A - E_a/RT$

This is a linear equation and from it we see that if we plot $ln\; k$ versus $1/T$ we will get a straight line with $slope = -E_a/R$ and $intercept = ln\; A$ .

Since we are not often interested in the pre-exponential factor A we can rewrite this equation to show the change from $k_1$ to $k_2$ when the temperature changes from $T_1$ to $T_2$ .

$ln\left(\frac{k_2}{k_1}\right) = \frac{-E_a}{R}\left(\frac{1}{T_2} - \frac{1}{T_1}\right)$

Example:

The conversion of cyclopropane to propene can be written as follows.

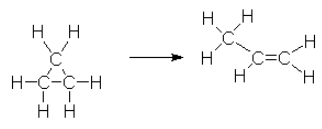
The following data was measured experimentally.

@300°C k = 2.41×10^-10 s^-1

@400°C k = 1.16×10^-6 s^-1

What is E_a?

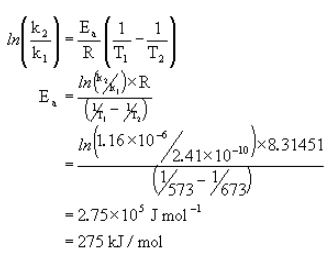
Now that we have the activation energy, we can calculate the rate constant at any other temperature using one known set of $k$ and $T$ .

What is k at 450°C?

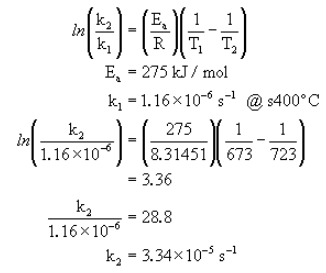
18.5: Reaction Mechanisms

We’re finally at the point where we can look at how rate laws and reaction mechanisms are related. We’ve seen that the balanced chemical reaction does not necessarily tell us anything about the actual rate law. That’s because the overall balanced chemical reaction represents only the initial state (reactants) and final state (products) and is not concerned with the process. Kinetics relates to the process.

If the reaction involves only a single step (elementary reaction) then there is a direct link between the reaction rate law and the ‘molecularity’ of the reaction itself. In other words, the rate law of an elementary reaction tells us exactly which molecules are involved. Since for a single step reaction, we can also relate this to the reactants, there is a correlation between the balanced reaction and the rate law for elementary reactions.

Let’s look at several examples of elementary reactions and consider the rate laws for them.

18.5.1: Unimolecular reactions (overall reaction order = 1)

This reaction requires 262 kJ/mol. This energy needs to be concentrated in the vibrations and rotations which are involved in the reaction.

Rate law: $Rate = k$ [C₄H₈]

In general for a reaction A products

$Rate = k$ [A]

18.5.2: Bimolecular reactions (overall reaction order = 2)

Here is an example of a bi-molecular reaction. This single step mechanism involves two molecules in the rate-determining step (in this case, it’s the only step).

NO(g) + O₃(g) → NO₂(g) + O₂(g)

Rate law: $Rate = k$ [NO][O₃]
The reaction is first-order with respect to both NO and O3. This implies one molecule of NO and one of O3 are involved in the reaction, exactly as the balanced reaction shows.
In general, for reaction

A + B → Products $Rate = k$ [A][B]

for reaction

2A → Products $Rate = k$ [A]²

18.5.3: Termolecular reactions (overall reaction order = 3)

Three molecules must collide with sufficient energy and all in the correct orientation. This is very rare. If the same reaction can be carried out using several bi-molecular steps then that is the way it will happen.

In general,

for reaction

A + B + C → Products $Rate = k$ [A][B][C]

2A + B → Products $Rate = k$ [A]²[B]

etc.

There are no higher order single step reactions.

18.5.4: Equilibrium Constants and Reaction Mechanisms

Consider the reaction mechanism

NO(g) + O₃(g) ⇄ NO₂(g) + O₂(g).

Since it has been determined that both forward and reverse reactions are single step reactions, it is easy for us to write the rate law for both reactions:

$Forward\; rate = k_f\mathrm{[NO][O_3]},$

$Reverse\; rate = k_r\mathrm{[NO_2][O_2]}.$

If the system is at equilibrium then we can state that the forward rate equals the reverse rate.

$k_f\mathrm{[NO][O_3]} = k_r\mathrm{[NO_2][O_2]}$

$\frac{k_f}{k_r} = \frac{\mathrm{[NO_2][O_2]}}{\mathrm{[NO][O_3]}}$

This is just the equilibrium constant.

Multi-step reactions are not so simple but still give proper values of K from stoichiometry.

18.5.5: Multi-step reactions

It has been experimentally determined that the chemical reaction (actually, we did it earlier in these notes)

2 NO + Cl₂ → 2 NOCl

Has a rate law of

$Rate = k \mathrm{[NO]^2 [Cl_2]}.$

We wish to try to create a model (reaction mechanism) that will explain this observed rate law. Our job as scientist is to find a model that works and to ensure that is it the best possible model.

Here is one possibility:

2 NO ⇄ N₂O₂	Fast equilibrium with equilibrium constant K1.
N₂O₂ + Cl₂ → 2 NOCl	Slow step with rate constant $k_2$

From the slow step:

$Rate = k_2\mathrm{[N_2O_2][Cl_2]}$

However, this rate law involves the concentration of N₂O₂ which is an intermediate in the reaction. It is neither a reactant nor a product. We need to try to replace this with some other function of concentrations of reactants.

The equilibrium is fast. Hence, we can always assume that the concentrations can be related to the equilibrium constant as follows:

$K_1 = \frac{\mathrm{[N_2O_2]}}{\mathrm[NO]^2}}$ ==> $\mathrm{[N_2O_2]} = K_1\mathrm{[NO]^2}$

We can now substitute this into the rate law we determined solely from the slow step.

$Rate = k_2K_1\mathrm{[NO]^2[Cl_2]}$

Or

$Rate = k\mathrm{[NO]^2[Cl_2]}$ where $k = k_2K_1.$

OK, So we found a rate mechanism that gives a match to the experimental mechanism. That is not proof that we got the right mechanism. A good researcher would then start looking for other mechanisms, hopefully never finding any that also match. This would make it more likely that the proposed mechanism is correct. Let’s try another possibility.

We can imagine that the following mechanism is plausible.

NO + Cl2 → NOCl + Cl slow – rate const. = $k_1$

NO + Cl → NOCl fast – rate const. = $k_2$

From the rate determining slow step:

$Rate = k_1\mathrm{[NO][Cl_2]}$ .

This is not the experimental rate law. This mechanism is not the correct one.

18.5.6: Steady State Approximation.

In this example, we will need to make some assumptions regarding intermediate concentrations in order to solve the problem.

The decomposition of N₂O₅ into NO₂ and O₂ is given by the following chemical reaction:

2 N₂O₅ → 4 NO₂ + O₂

and has an experimentally observed rate law of $rate = k\mathrm{[N_2O_5]}$ .

Since it is obvious that we need at least two molecules of N₂O₅ to complete one molecule of oxygen we cannot pretend that this rate law indicates a single step reaction even if we can write the balanced reaction with a coefficient of 1 in front of the N₂O₅.

There must be multiple steps involved in this chemical process. To determine what the actual mechanism might be, one simply makes educated guesses as to the mechanism and then determines the rate law from the postulated mechanism. If the rate law of the postulated mechanism matches that determined experimentally, we have evidence (not conclusive) that the postulated mechanism is the actual one.

For this reaction a postulated mechanism involves the following single-step reactions.

N₂O₅+ M ⇄ N₂O₅* + M activation step 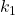$k_1$ and $k_{-1}$ .

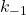The molecule with the asterisk * is activated. Because of the collision with M, it now has enough energy to react. It’s just a matter of time for the energy to find its way to the correct bond to break and move forward, or to dissipate and go back to the start.

This step is the activation step, where some molecule M collides with the N₂O₅ and gives it sufficient energy to react.

N₂O₅* → NO₂ + NO₃ slow; $k_2$
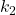
NO₂+ NO₃ → NO + NO₂ + O2 fast
NO + NO₃ → 2 NO₂ fast

Since the fast reactions are essentially ‘held up’ by the slow steps. it will be the slow steps that determine the reaction rate. Obviously, we need to deal with the fact that there are two steps, neither of which is clearly the rate-determining one.

We can almost think of this as a two step process where the rates are comparable. We can get several differential rate equations from this system.

From step 1:

$\frac{d\mathrm{[N_2O_5]}}{dt}= -k_1\mathrm{[N_2O_5][M]} + k_{-1}\mathrm{[N_2O_5^*][M]}$
$\frac{d\mathrm{[N_2O_5^*]}}{dt}= k_1\mathrm{[N_2O_5][M]} - k_{-1}\mathrm{[N_2O_5^*][M]} - k_2\mathrm{[N_2O_5^*]}$

and, assuming that the steps 3 and 4 go to completion immediately, we can use the overall stoichiometry to determine one more rate equation.

$1/2\frac{d\mathrm{[NO_2]}}{dt}= k_2\mathrm{[N_2O_5^*]}$

We have a seemingly intractable problem since there are more unknowns than equations. However, there are simplifying possibilities.

If we have a large excess amount of M molecules (High Pressure system) that are available to activate the N2O5 then the activation step (1) will be faster than the first dissociation step (2) involving the activated molecule N2O5*. In this case, the rate can be determined from the slow step (2) and would be quite simply

$Rate = k_2 \mathrm{[N_2O_5^*]}$ . and using the equilibrium from step 1, we can easily get

$K_1 = \frac{k_1}{k_{-1}} = \frac{\mathrm{[N_2O_5^*]}}{\mathrm{[N_2O_5]}}$

$Rate = K_1k_2\mathrm{[N_2O_5]} = k\mathrm{[N_2O_5]}$ .

This implies that there is only one molecule of N₂O₅ involved in the rate determining step. While, even in this multi-step reaction, that may be true, there is no guarantee that we can relate reaction order to molecularity in a multi-step reaction.

In low or intermediate pressure cases, we cannot make the simplifying assumption that step 2 is rate determining. we need to consider both the activation step and the dissociation steps together.

N₂O₅* is produced and destroyed by the activation step and also used up in the dissociation step. The first assumption we will need to make is to assume that the amount of the activated molecules N₂O₅* will quickly reach a value that remains constant throughout the reaction. This is a steady-state and is written mathematically as

$\frac{d\mathrm{[N_2O_5^*]}}{dt} = 0 = k_1\mathrm{[N_2O_5][M]} - k_{-1} \mathrm{[N_2O_5^*][M]} - k_2\mathrm{[N_2O_5^*]}.$

The zero value means we’ve assumed no change in concentration over time, not zero concentration.

Now, we can solve for [N₂O₅*]

Now, using equation 3 above, we can solve for the overall rate.

We see that at low pressure (small amounts of M) we can assume that k-1[M] is small compared to k2 (in the denominator) and our expressions simplifies to

$rate = k_1\mathrm{[N_2O_5][M]}$

at high pressures, the reverse is true and we get

$rate = \frac{k_1k_2}{k_{-1}}\mathrm{[N_2O_5]} ,$

which is the same form as we predicted in our first simplification above.

18.5.7: Rate and temperature dependence

2 NO(g) + Cl₂(g) → 2 NOCl(g)

the experimental rate law is: $rate = k\mathrm{[NO]^2[Cl]}.$

While we might use this as evidence that the reaction is a single step one since the rate law and the exponents match. This would be a ter-molecular reaction. If it is possible to come up with a multi-step system which avoids ter-molecular steps and still has this same rate law then the reaction is more likely to go via the multi-step route.

Here’s an example of another mechanism. In addition, we’ll look at the temperature behaviour of the reaction.

2 NO + O₂ → 2NO₂

Has a rate law

$Rate = k \mathrm{[NO]^2[O_2]},$

where k decreases with increasing temperature!

The following mechanism explains both the rate law and the apparent anti-Arrhenius behaviour.

NO + NO ⇄ N₂O₂	Fast equilibrium with forward/reverse rate constants $k_1/k_{-1}$
N₂O₂ + O₂ → 2 NO₂	Slow step rate constant = $k_2$ .

The second (slow) step is rate determining so

$Rate = k_2 \mathrm{[N_2O_2] [O_2]}.$

Just like the previous example [N₂O₂] is an intermediate, not a reactant or product. It would be very hard to measure this concentration with any certainty. We will reformulate the rate law in a way that uses only reactant (or product) concentrations.

Since the first equilibrium step is fast, we can say that the system is always at equilibrium, hence

forward rate = reverse rate

$k_1 \mathrm{[NO]^2} = k_{-1} \mathrm{[N_2O_2]}$

or

$\mathrm{[N_2O_2]} = K_1 \mathrm{[NO]^2}$

where the equilibrium constant $K_1 = k_1/k_{-1}$ .

Now we can rewrite the overall rate constant as

$Rate = k \mathrm{[NO]^2[O_2]}$ where $k = k_2K_1$ .

Since K1 is an equilibrium constant, we can write

$K_1 = exp\left[\frac{-\Delta G_1^\circ}{RT}\right] = exp\left[\frac{-\Delta H_1^\circ - T\DeltaS_1^\circ}{RT}\right]$

NOTE: $exp[x]$ is the same as writing $exp^x$ .

Rearranging gives

$K_1 = exp\left[\frac{\Delta S_1^\circ}{R}\right]\times exp \left[\frac{\Delta H_1^\circ}{RT}\right]$

now, combining this with the equation for k above, gives

$k=k_1K_1 = A_2 \exp\left[\frac{-E_{a2}}{RT}\right]\times \exp \left[\frac{\Delta S_1^o}{R}\right] \times \exp \left[\frac{\Delta H_1^o}{RT}\right]$

Now, let’s group terms under the common denominators in the exponents. Remember to add the exponents when we multiply the values.

$k = \overset{A_{\mathrm{eff}}}{\overbrace{A_2 \;\exp\left[\frac{\Delta S_1^\circ}{R}\right]}} \times \exp\left[\frac{-(\overset{E_{\mathrm{a,eff}}}{\overbrace{E_{a2}\;+\;\Delta H_1^\circ}})}{RT}\right]$

We have grouped the factors based on their temperature independence. Notice that if we rename the first factor to be simply $A_{eff}$ and the numerator of the exponent to be an ‘effective’ activation energy Ea,eff, we can now write an equation that looks like the Arrhenius equation.

$k = A_{\mathrm{eff}}\; \exp \left(\frac{-E_{\mathrm{a,eff}}}{RT}\right)$

where

$A_{\mathrm{eff}}=A_2 \;\exp\left[\frac{\Delta S_1^\circ}{R}\right]$

is temperature independent and is an effective pre-exponential factor A for the overall rate law and the part

$E_{\mathrm{a,eff}}=E_{a2}+\Delta H_1^\circ$

in the exponent in the second factor is like an effective reaction barrier $E_{\mathrm{a,eff}}$ .

This looks like a normal Arrhenius equation except that the effective activation energy $E_{\mathrm{a}}$ is the sum of $E_{\mathrm{a,2}}$ plus $\Delta H_1^\circ$ . Since $\Delta H_1^\circ$ can be positive or negative the sign of the overall $E_{\mathrm{a}}$ could be negative if $\Delta H_1^\circ$ is negative enough. In this case, step 1 is highly exothermic. This would give an effective negative energy barrier and the observed anti-Arrhenius behaviour.

An alternative view of this can be seen in light of Le Châtelier’s principle. The equilibrium in step 1 is supplying reactant for step 2. Since the position of the equilibrium shifts to the left as the temperature is increased (Energy is a product of step 1) then the supply (concentration) of reactant for step 2 (the rate-limiting step) decreases as the temperature increases. If the concentration change is large enough, the rate of step two will decrease even as the temperature rises.

18.6: Catalysis

A catalyst is a substance which increases the rate of a reaction but is not consumed in that reaction and does not change the products of reaction. A catalyst may well be used in the reaction at some step in the reaction mechanism but if so, it is then regenerated at a later step. Hence, no net change in the amount of catalyst occurs. In some cases, the catalyst is simply a compound or chemical species which is in the same phase as the reaction mixture itself. This is called a homogeneous catalyst. Other catalysts exist as a separate phase and the reaction occurs on the phase boundary (surface) between the reaction mixture and the catalyst. This is called a heterogeneous catalyst.

An example of homogeneous catalysis can be found in the reaction which sees cis-2-butene transforming to trans-2-butene.

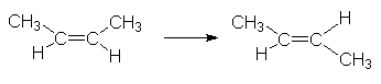
This reaction has a rate that is relatively slow and an activation energy $E_a$ = 262 kJ/mol.

If we add Iodine, I₂, to the reaction mixture we find that the activation energy is lowered to $E_a$ = 115 kJ/mol.

This can be explained by the following reaction mechanism.

Iodine sets up its own equilibrium with the iodine radical.

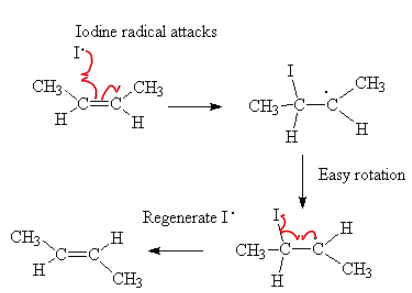
$\mathrm{I_2} \rightleftarrows \mathrm{2 I^.}$

We see that the iodine radical was used in the reaction, caused a different reaction mechanism to occur. This new mechanism has a lower activation energy than the uncatalyzed one. The iodine radical is regenerated at the end of the mechanism and hence is not used up but it is used.

A heterogeneous reaction most often involves a solid catalyst and a liquid or gaseous reaction mixture. Consider the catalytic converter in the exhaust system of your automobiles. Platinum metal is coated on a granular support material to ensure that as much platinum as possible is exposed to the fumes passing through the exhaust system. These fumes often contain unburned hydrocarbons and CO and NO gases. The catalyst helps complete the oxidation of these to CO2, NO2 and H2O. You often notice lots of water vapour coming from the exhaust systems of modern vehicles on a cold day because it condenses in the cold air to become visible.

I will illustrate a heterogeneous catalysis with the following example.

C₂H₄ + H₂ → C₂H₆ Very slow without a catalyst.

Use Pt or Ni catalyst.

Our bodies use catalysts called enzymes to facilitate many kinds of reactions. For example, the oxidation of sucrose C₁₂H₂₂O₁₁ to carbon dioxide and water only occurs at high temperature (sucrose burns) unless there is a catalyst present. The enzyme sucrase (a code name meaning “we don’t know what it is but it catalyzes the sucrose reaction”) makes this process quite rapid at body temperature (lower activation energy). The catalyzed reaction at body temperatures is on the order of 10²⁰ times faster than the uncatalyzed one.

These types of catalytic reactions are not quite heterogeneous like the metal-catalyzed reactions are since the enzymes are dissolved in the same solutions as the reactants and products but their size is so large that they are almost like a solid phase in comparison to the tiny reactants and products. This type of reaction is usually simply classified as an enzyme-catalyzed reaction.

Practice problems for Kinetics

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

18.1: Introduction

18.2: Reaction Rate

18.3: Rate Laws and Reaction Order

18.3.1: Initial Rate Method

18.3.2: Integrated Rate law method

18.3.3: Half-life

18.4: Temperature and Reaction Rate

18.4.1: Arrhenius Equation

18.5: Reaction Mechanisms

18.5.1: Unimolecular reactions (overall reaction order = 1)

18.5.2: Bimolecular reactions (overall reaction order = 2)

18.5.3: Termolecular reactions (overall reaction order = 3)

18.5.4: Equilibrium Constants and Reaction Mechanisms

18.5.5: Multi-step reactions

18.5.6: Steady State Approximation.

18.5.7: Rate and temperature dependence

18.6: Catalysis

License

Share This Book