8 Phase Transitions
Michael Mombourquette
8.1: Introduction
There are many properties of matter which is intrinsic to the matter itself. One of these properties is called the state of the matter. The three most common states of matter that we encounter on a daily basis is solid, liquid and gas. Superheated material where the electrons and nuclei are completely stripped off each other (as in the corona of the sun) are called plasma but this is not really of concern to us chemists. Some people claim that materials called liquid crystals are another phase of matter. Liquid crystals are more like a special material that exists with properties of both liquid and solid.
Except for Helium, all gases, when cooled, eventually condense to liquids and then to solids. All liquids are volatile to some extent and evaporate to become gases (not all liquids can be boiled since some will break down from the heat long before they get hot enough to boil).
We often use the word vapour to represent the gas which evolves off a liquid as a result of the vaporization process. Gas and Vapour are identical from the chemical viewpoint although we often use them in common speech with subtly different connotations. Specifically, gas is often used (here in North America) as an abbreviation for the petroleum product called gasoline which is a liquid. Fluid is another confusing term. It could be either a liquid or a gas. It merely indicates a property of the material that allows it to flow, as in a river flows or a stream of gas flows.
The transformation of one material to another is called a phase change.
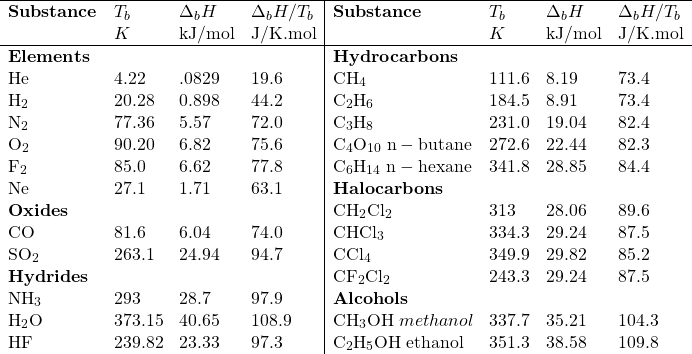
 |
| Figure: Diagrammatic representation of Phase Changes. The vertical axis represents energy. |
To go from solid to liquid (to gas) (the arrows on the left-hand side of the figure) one must increase the internal energy (KE) of the substance until the molecular forces binding them in their condensed phase are broken. Thus, the phase a material exists in at any given temperature and the ease with which it can be transformed to another phase is a function of the intermolecular forces that exist.
8.2: Vapour Pressure
Consider for the moment a liquid. According to the kinetic molecular theory, there will be a range of kinetic energies for any given temperature (just as in the gases). Some molecules will contain high Translational Kinetic Energy (ɛ) while others will contain relatively low ɛ. If any given molecule has sufficient kinetic energy that it can break the intermolecular forces holding it in the liquid then it can move out of the liquid into the gas. As the temperature of the liquid in raised. the fraction of molecules which have sufficient ɛ to exist in the gas phase increases.
We can measure the tendency of the liquid to form gas molecules by simply measuring the pressure of the gas which develops when in contact with the liquid.
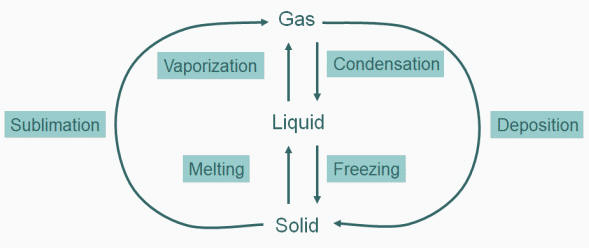
 |
| Figure: Illustration of Vapour Pressure. The flask on the left shows initial condition of a liquid in an evacuated flask. The molecules will have a range of kinetic energies. Some of the liquid molecules may have enough energy to escape the intermolecular forces of the liquid into the gas phase. As more molecules enter the gas phase, some of them will begin re-entering the liquid phase as they lose energy to other gas molecules in collisions. Eventually, the number of molecules per second entering the gas phase from liquid and the number per second entering the liquid phase from the gas are equal. The pressure measurable in the flask at this equilibrium point is the vapour pressure. |
We could imagine that since heat is exchanging between individual molecules continuously that individual molecules in the liquid phase could through collision gain enough energy to move to the gas phase. This would have the effect of lowering the average kinetic energy (temp) of the liquid (we cool off by perspiration evaporating of our skin using this process). Simultaneously, molecules in the gas phase can, by collision, lose energy and fall back into the liquid state. This process accounts for the condensation we see on cold surfaces (like your car windows in the morning). At equilibrium, the rate of molecules leaving the liquid phase for the gas phase (vaporization) is equal to the rate of condensation from the gas to the liquid phase.
An alternate way of looking at this is the thermodynamic approach. We will discuss the details of this later in the course. For now, let’s accept that it is a universal trend that things tend to attain maximum entropy (defined here loosely as the amount of motional freedom the molecules have). In general, we give a substance greater entropy by giving it energy and we lower the entropy of a material by removing energy. If the energy supply is such that the overall temperature is constant then, since gas molecules have higher entropy (less restrictions on their positions) than their liquid counterparts, we expect that there is a trend for liquids to spontaneously vaporize. On the other hand, another law of thermodynamics (which we’ll discuss later) states that heat flows from warmer bodies to colder bodies. In other words, the warm vapour molecules will tend to lose energy and return to the liquid state if there is a cooler body around that will accept their excess kinetic energy.
Since the process of evaporation also involves the breaking of intermolecular forces, it is reasonable to expect that if there are strong intermolecular forces in the liquid phase then a molecule will require higher kinetic energy to be able to break out of the liquid phase. This will have an effect on the measurable vapour pressure.
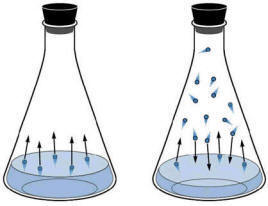
The molecules have a distribution of kinetic energies as can be seen in the diagram below. Clearly, the higher temperature liquids will have more molecules that can break the intermolecular forces and hence, the vapour pressure will be higher in the higher temperatures. Alternatively, as the energy needed to escape the liquid rises, the number of molecules that can escape the liquid phase will lower.
Thus, higher intermolecular forces means lower vapour pressures and higher temperatures means higher vapour pressures.
 Figure: Distribution of molecular speeds at three different temperatures. Blue represents a sample of cooler molecules, black is an intermediate temperature and red is a higher temperature. Clearly, the higher temperature sample has a higher number of molecules with the higher energies needed to escape the liquid phase. |
The Boltzman distribution equation that relates the distribution of the molecular speeds (and hence kinetic energies) as a function of temperature. |
This dependence of the vapour pressure on temperature is reflected in the Clausius-Clapeyron equation.
![]()
This equation shows the relationship between the vapour pressure and the enthalpy of vaporization (ΔvH) of a substance at two temperatures T1 and T2. The enthalpy of vaporization is in essence a measure of the amount of energy needed to transform one mole of the substance from liquid phase to the gas phase. This equation can be used to determine ΔvH if we measure a vapour pressure at two different temperatures. We can also use a known value of ΔvH to determine a vapour pressure of a substance at any desired temperature, if we know it at one temperature.
Example: What is the vapour pressure of water at 20℃ if the measured value for ΔvH is 44 kJ/mol?
This question seems a bit too sparse of information, since there is only one temperature/pressure mentioned here, until we recall that we can use the defined boiling point for water of 100℃ at 1 atm pressure as our second temperature/pressure point. Thus, the vapour pressure of water at 100℃ is 1 atm. We now have enough information to use the Clausius-Clapeyron equation.
![]()
Thus, P*(H2O,20℃) = 0.0208 atm
Similarly, we could calculate the vapour pressure at any temperature:
Thus, P*(H2O,0℃) = 0.0055 atm
Note that as T goes down, so does P*.
We can use this information to understand some everyday phenomenon. some people find that they get itchy skin or chapped lips in winter but not in summer. If we look at the relative vapour pressured at the two temperatures shown here, we see that in winter, the partial pressure of water is much lower than in summer.
8.3: Phase Changes
Phase changes involve the exchange of heat into or out of the system. For example, to change from a condensed phase to a less condensed phase, heat will have to be absorbed by the system. For the reverse phase change, heat is released by the system. This is because of several factors, including intermolecular forces and packing (in solids).
Consider an experiment where we have a substance, initially in the solid phase, in a constant pressure experiment. The substance is heated at a steady rate. The molecules steadily gain kinetic energy. Eventually, the molecules will gain enough kinetic energy so that some of them can change to a less condensed phase (say, liquid). At this point, While this process happens, kinetic energy (temperature) is being changed into potential energy as intermolecular forces are being broken and into entropy as the molecules begin to have more freedom of motion. Thus, the process will happen at a rate that is just sufficient to use the heat energy as it is being supplied without lowering the temperature or allowing it to rise. We can observe this using a heating curve, where we plot the temperature as a function of time (∝ Energy) (See Figure below).
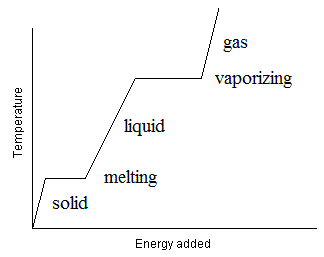
Figure: Heating curve showing the temperature of a pure substance as heat is applied at a steady rate and under constant pressure conditions. The places where the temperature remains constant for a period of time reflect conditions where a phase change is occurring so that the added heat is used up by the molecules as they change phase. Other places, where the temperature is rising, no phase changes are occurring so the heat added is going to increasing the kinetic energy of the substance. Thus, this substance has two phase changes, one from solid to liquid (melting) and the other between liquid and gas (vaporizing). Note that the slopes of the pure solid, liquid and gas Temperature versus time (energy) region is not the same. This is because the heat capacity of the three phases differ from each other.
Melting
When a solid melts to form a liquid, there is generally very little volume change involved (compared to the volume change in boiling). This is because only some of the intermolecular forces in the solid are broken in the phase change. additionally, the solid’s packed structure is broken up and this contributes a large part of the energy needed to melt the material. Packing energy is largely an entropy feature, where the individual molecules suddenly have a larger degree of freedom of motion available to them. This increase in entropy of the system requires that the system absorb energy from the surroundings. For the reverse phase transition, freezing, the system becomes more ordered (entropy is lowered) and energy is released to the surroundings. Thus, while intermolecular forces do play a significant role in this process, entropy also plays a role.
Because there is some volume change in the process, there will be a pressure dependence as well as a temperature dependence. For example, most materials increase in volume as they melt. If we apply sufficient pressure to the material, we may force the molecules to remain packed together even as the temperature is raised past the melting point we might expect for a lower pressure experiment, conversely, if the pressure is lowered, the molecules may find themselves melting at a lower temperature as the energy needed to unpack (increasing the volume) becomes lower. We’ll revisit this point later in the phase diagrams section.
The melting point is defined as the temperature at which both the solid and the liquid can exist in equilibrium at a certain pressure.
Boiling
When the molecules of a liquid break free of all intermolecular forces and separate from each other, they become gases. This phase change is called boiling. For this phase change, there will be a significant effect of the strength of the intermolecular forces as breaking these constitutes a very large part of the process. However, entropy changes are also large as the volume change involved in this phase change are generally quite large. Thus, there will be a larger effect of pressure on the equilibrium between liquid and gas. This manifests itself as a lower slope on the single component phase diagrams we will explore later.
The boiling point is defined as the temperature at which the vapour pressure of the liquid is equal to the external pressure. Note that at the boiling point, the liquid is actually at equilibrium and is not noticeably changing phase. We are familiar with boiling pots of water where the water is bubbling rapidly as it changes into the gas phase. This can only happen if we heat the water to “above” the boiling point. At this temperature, the system is not at equilibrium and tries to rapidly reach equilibrium by changing phase from liquid to vapour.
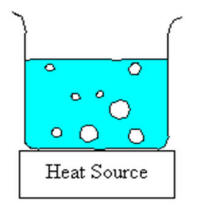
Figure: Illustration of a boiling pot of water. Since the bubbles of vapour form at the bottom of the pot and must be pure vapour, the internal pressure of the bubble must be equal to (or slightly greater) than the external atmospheric pressure. In fact, it must be high enough to overcome the additional pressure caused by the weight of the liquid above it, surface tension. etc.
In addition, there must be some irregularity or defect in the container to act as a nucleation point around which the bubble can start to form. In a perfectly smooth container where the liquid is heated slowly with no stirring, it is possible to superheat the liquid to above its boiling point. This dangerous condition can lead to explosive boiling of the liquid if a nucleation is suddenly induced by, say, shaking the pot or throwing something into it. In Chemistry where we boil water in (relatively) smooth glass containers, we normally use chips of inert ceramic called boileezers to help induce bubbling and prevent superheating the liquid. Click here for an illustrative video.
.
The normal boiling point (NBP) is the temperature at which the vapour pressure of the liquid is equal to 1 atmosphere (101.325 kPa). There is also a standard boiling point, defined as the temperature at which the vapour pressure is equal to 1 bar (100 kPa). While the two defined boiling points are generally close, they are not quite the same. Generally, we use the NBP for our work, even though it is based on a non-SI unit of pressure.
We expect, just as in vapour pressure, that the boiling point of a liquid is higher if the intermolecular forces in the liquids are higher. In addition since the boiling is done against a constant external pressure P ext. we expect that if the external pressure is higher then so too will be the boiling point and vise versa. (This is the principle used to speed up the cooking processes by using a pressure cooker. The water in the cooker can be heated to higher than the normal boiling point because of the higher pressures inside the cooker and hence the food cooks faster at the higher temperature.)
8.4: Intermolecular Forces
We would like to try to explain the observed phase-change behavior of different materials. For example, water (18 g/mol) is a liquid at ambient conditions but methane (16 g/mol) is a gas. The explanation requires an understanding of the intermolecular forces that are involved.
The general category for most intermolecular forces is “van der Waal’s Forces”. These include several different types of intermolecular forces (London, dipole-dipole, hydrogen bonding) as described below. We would expect that the stronger the intermolecular forces, the higher will be the melting points and boiling points of the substance.
8.4.1: London forces (weak)
 London (a.k.a. dispersion) forces are the weakest of the intermolecular forces. They involve molecules that have no permanent dipole moments. The interaction forces arise because of temporary dipoles that can occur in the individual molecules. Temporary dipoles occur as the electron cloud moves (changes its dispersion) within the molecules. All molecules can have some level of London (dispersion). In molecules with tightly held outer electrons, the dispersion of the electrons is very small and the London forces are therefore very small. Other molecules, which have loosely held outer electrons can find their electron dispersion distorted fairly easily, creating temporary dipoles and hence measurably higher intermolecular forces.
London (a.k.a. dispersion) forces are the weakest of the intermolecular forces. They involve molecules that have no permanent dipole moments. The interaction forces arise because of temporary dipoles that can occur in the individual molecules. Temporary dipoles occur as the electron cloud moves (changes its dispersion) within the molecules. All molecules can have some level of London (dispersion). In molecules with tightly held outer electrons, the dispersion of the electrons is very small and the London forces are therefore very small. Other molecules, which have loosely held outer electrons can find their electron dispersion distorted fairly easily, creating temporary dipoles and hence measurably higher intermolecular forces.
Hence, molecules like H2 or He, have very small London forces and we observe very low phase change temperatures for these substances. These two only freeze close to absolute zero. In fact, helium, will only solidify under high pressures (25 atm or so).
Other non-polar substances have larger outer electron clouds and hence stronger London forces. For example, methane (CH4) is a gas but butane (C4H10) is a liquid at room temperature. The difference in these two is, in part because the butane is heavier but it mostly because the electron cloud in the butane is bigger.
8.4.2: Dipole-dipole forces (medium)
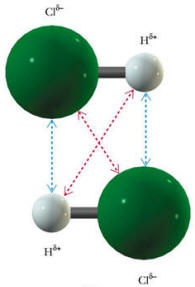 Many molecules have permanent dipoles because of individual bonds being not 100% covalent. Take for example, H-Cl. This molecule is made of two different atoms, having two quite different electronegativities. Thus, the chlorine end of the molecule will be more negative than the hydrogen end. In this case, we will have attractive forces between two different molecules that are permanent and based only on the relative orientation of the neighboring molecules. A low energy configuration for two molecules (show here) would align the positive end of one molecule with the negative end of the other.
Many molecules have permanent dipoles because of individual bonds being not 100% covalent. Take for example, H-Cl. This molecule is made of two different atoms, having two quite different electronegativities. Thus, the chlorine end of the molecule will be more negative than the hydrogen end. In this case, we will have attractive forces between two different molecules that are permanent and based only on the relative orientation of the neighboring molecules. A low energy configuration for two molecules (show here) would align the positive end of one molecule with the negative end of the other.
The blue arrows represent the attractive forces and the red arrows, the repulsive forces. In general, the attractive forces will be stronger than the repulsive forces. Molecules with permanent dipoles will tend to have higher melting and boiling points than similar-sized molecules that are non-polar.
8.4.3: Hydrogen bonding (strong)
In solids and liquids, hydrogen bonding can occur between a hydrogen atom bonded directly to either F, O or N to the lone pair on an F, O, or N from another molecule. The hydrogen, which is partially positive because of the high polarity of the bond to N, O or F, is attracted to the lone pair on another N, O or F. No other atom bonded to H can cause hydrogen bonding. Thus, Ethane C2H6 (London forces only) is a gas whereas Ethanol C2H5OH (dipole-dipole and hydrogen bonding) is a liquid under ambient conditions.
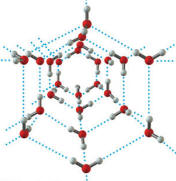
Hydrogen bonding in water is so strong that it actually forces the crystal structure of the ice to take up a larger volume than the same amount of liquid water occupies. Thus, ice is less dense than water so it floats. This behavior is rather important for the existence of life on earth. If, ice sank when it froze, the oceans would quickly have filled up with solid ice that would only melt a bit near the top each summer under the sun’s rays. Even at the equator, the depths of the ocean would be mostly solid as the sun’s heat would never reach to melt the deep ice. Life would probably not have evolved at all under those conditions.
8.5: Other Properties
8.5.1: Viscosity
The viscosity of a liquid is a measure of the ease with which a liquid can flow. A high viscosity liquid is a slow flowing liquid and a low viscosity liquid flows more quickly. Viscosity is related to the intermolecular forces in a liquid. It is also related to the mass and shape of the molecules.
The molecule glycerol C3H8O3 has three OH groups, one on each carbon and can form lots of H-bonds to neighboring glycerol molecules. Glycerol is a very thick viscous liquid (like molasses) compared to much less viscous motor oil of similar or even higher molecular weights.
High molecular weight molecules that are long and flexible tend to be very viscous, to the point of being solid (wax). Such molecules tangle in each other and cannot move relative to each other very easily.
8.5.2: Surface Tension

The surface tension is the energy needed to increase the surface area of a liquid. If a liquid has high intermolecular forces, the surface tension will be strong and the liquid will tend to try to minimize its surface area: a rain drop in the air is mostly spherical, distorted somewhat by the friction with the air as it drops. We can float small objects on the surface of water because we are actually increasing the energy by ‘denting’ the surface. The water tries to lower it’s energy by forcing the surface to become planar again, thus pushing back on the object. Small objects like some insects can ‘walk on water’ because of the force caused by surface tension.
8.6: Phase Diagrams
If we map out the phase of a substance as a function of temperature and pressure, we will get a picture of its behavior that is very informative. The following image represents a phase diagram for water (not to scale), where certain properties of water are indicated.
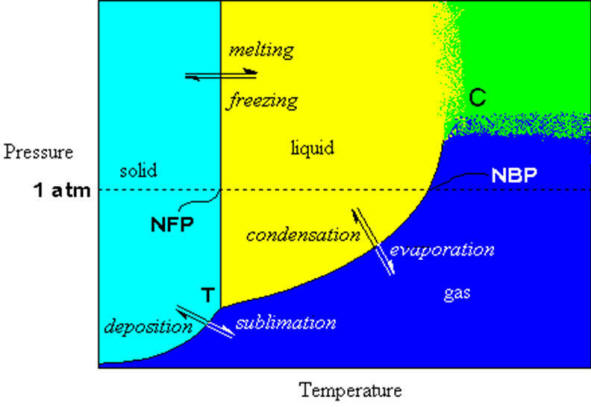 Figure: Phase diagram of water. Blue area represents the gas phase, yellow area is the liquid phase, cyan area is the solid. the green region represents the critical region in the phase diagram where it is not possible to distinguish between gas and liquid. Words in italics represent the process (double arrows). letters in Ariel Font mark special points on the graph and normal text labels the regions and the axes. Figure: Phase diagram of water. Blue area represents the gas phase, yellow area is the liquid phase, cyan area is the solid. the green region represents the critical region in the phase diagram where it is not possible to distinguish between gas and liquid. Words in italics represent the process (double arrows). letters in Ariel Font mark special points on the graph and normal text labels the regions and the axes. |
The black lines in the figure represent the precise pressure/temperature conditions where more than one phase can occur simultaneously. for example, at exactly zero degrees Celsius and one atmosphere pressure, water and ice can exist together in equilibrium. Notice the dotted line representing the 1 atm pressure level. The point where it crosses the phase boundary between liquid and solid is defined to be zero degrees Celsius (0℃). Where it crosses the line dividing the liquid from the gas phase, the temperature is defined to be one hundred degrees Celsius (100℃).
Let’s look at the liquid/solid phase dividing line first. On the scale shown here it seems that there is no pressure dependence on freezing point (the line seems vertical). The steepness of the line is because the density of the solid and the liquid are nearly the same. Because ice is less dense than liquid water, the solid/liquid line for water is tilted slightly back so it has a very high negative slope. In other words, as the pressure increases, the melting point goes down. However, the actual amount of pressure required to lower the melting point by even one degree is very large. This lowering of melting point with increased pressure is a result of the increase in volume (lower density) that water experiences upon freezing. Most materials become more dense upon freezing and would exhibit a raising of the melting point with higher pressures.
| There is an old misconception that states that the reason hockey players can skate is that the increased pressure under their blades causes the ice to melt, lowering the friction so that the blade can glide easier. Simple calculations shows that even the fattest person in the world doesn’t weigh enough to lower the melting point more than a fraction of a degree. Obviously, some other explanation for the slipperiness of ice needs to be developed. Besides; how does the puck slide so easily? |
Now look at the liquid/vapour boundary one can see that there is a definite pressure dependence… lower the applied pressure and the boiling point is lowered, raise it and it is raised.
The line dividing the solid from the gas represents the sublimation/deposition phase transitions. This phase transition only occurs (exclusive of all others) at low pressures. This property often used in food processing to dry out the water from a food without heating it. The water is driven off by freezing the food, lowering the pressure and then slowly applying heat to it such that the water sublimes directly to the gas phase without ever forming a liquid. You’ve heard of freeze-dried coffee? well that’s how they do it. The only other way to drive off water is to heat it to the boiling point and evaporate all the water. This also changes the consistency and taste of the food.
There are also two special points on the graph, labelled T and C. They are the triple point and the critical point, respectively.
The triple point represents the pressure/temperature conditions where the solid, liquid and gas phases can exist in equilibrium with each with each other. This is most easily attained by slowly lowering the temperature of the liquid in contact with its own pure vapour. The liquid/vapour will be in equilibrium (providing the temperature is lowered slowly enough) when the freezing begins. Thus the three phases will be all in equilibrium at this point. This is the triple point. There can be more than one triple point in some phase diagrams, if and only if, there are more than three phases for the substance. In the phase diagram for water shown below, we see many different solid phases and many triple points, mostly joining three different solid phases.
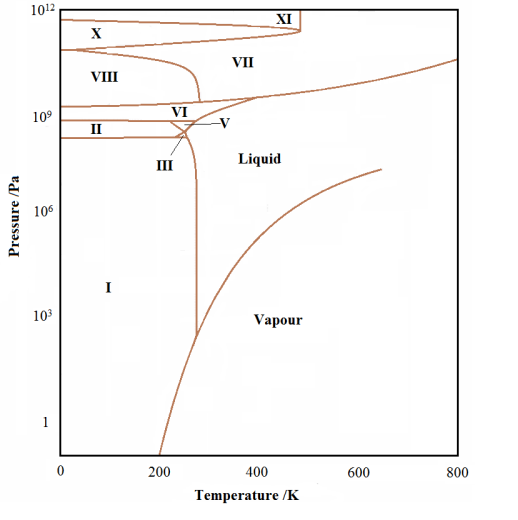
The experimental phase diagram for water showing the different solid phases |
The other special point is the critical point. This point represents the highest temperature point on the vapour/liquid phase transition curve. At pressures and/or temperatures higher than that (green area in the figure above) it is not possible to distinguish between the two phases. To understand this point, consider a system in equilibrium, i.e., tracing along the liquid/vapour curve. As the temperature is raised, the vapour pressure of the liquid rises rapidly. This means that the molar volume of the vapour decreases rapidly, i.e., the density increases. Eventually, the molar volume of the vapour and of the liquid are equal and there is no discernable difference between the physical properties of the two and so we can see no border between liquid and vapour. Beyond this point, the substance is called a supercritical fluid.
Boiling point ![]() and Enthalpy of vaporization(boiling)
and Enthalpy of vaporization(boiling) ![]() (a.k.a.,
(a.k.a., ![]() )
)