16 REDOX and Electrochemistry
16.1: Oxidation Numbers and REDOX Balancing
16.1.1: Assigning Oxidation Numbers
Oxidation numbers (ON) are not real charges. They are the results of an accounting method whereby we can keep track of electrons during a chemical reaction. In a few cases, the ON is actually a real charge but only in rare monatomic ions like Cl– and Na+.
Oxidation numbers are defined using two premises.
- The bonds in compounds for which you wish to assign oxidation numbers are assumed to be 100% ionic in nature.
- The electrons in the bonds are thus divided such that the more electronegative element gets both electrons in a bond and the less electronegative element ends up with a net loss of electrons.
 Using this method, we need to be up on the relative electronegativities of the elements and it takes time to figure out which way the electrons go and the resulting charges. For example, if we take the bonds in water H2O. There are two O–H bonds in each molecule.
Using this method, we need to be up on the relative electronegativities of the elements and it takes time to figure out which way the electrons go and the resulting charges. For example, if we take the bonds in water H2O. There are two O–H bonds in each molecule.
 Taking them one at a time, in an O–H bond, there two electrons and we assign them both to the oxygen since it is more electronegative than hydrogen. Doing this to the second bond as well leaves us with an oxygen ion with 8 electrons for a net charge of –2 and two hydrogen ions with no electrons for a net charge of +1. This takes considerable thought processes and can be simplified using a set of rules based on these processes but which gives results directly.
Taking them one at a time, in an O–H bond, there two electrons and we assign them both to the oxygen since it is more electronegative than hydrogen. Doing this to the second bond as well leaves us with an oxygen ion with 8 electrons for a net charge of –2 and two hydrogen ions with no electrons for a net charge of +1. This takes considerable thought processes and can be simplified using a set of rules based on these processes but which gives results directly.
RULES: (taken in order of importance.)
- The sum of the oxidation numbers (ON) of the atoms in a species (ion, molecule, atom) is equal to the charge on that species.
For example,
He(atom) —> ON = 0
H2(molecule) —> both atoms must have ON=0 so sum is 0
Cl– (ion) —> ON = –1
Na+ (ion) —> ON = +1 - Alkali metals in a compound with non-metals have ON=+1
example: NaCl —> ON(Na) = +1\ON(Cl) = –1 [rule 1] - Alkali Earth metals in a compound with non-metals have ON=+2
example: MgO —> ON(Mg) = +2 \ON(O) = –2 [rule 1] - Hydrogen in cpds. has ON = +1
- Halogens have ON=–1 as in HF or HCl. This is always true for fluorine but not always true for the others, if the other halogens are bonded to other halogens [interhalogen] or to oxygen then the more electronegative atom gets the negative charge.
example ClO– —> ON(Cl) = +1, not –1. O gets the negative charge (-2 in the case of O) because O is more electronegative than Cl. - Oxygen in compounds is always ON(O)=–2. Except with Fluorine (rule 5) or in the case of peroxides O22– [ON(O)=–1] or super oxides O2– [ON(O) = –1/2].
- For all elements where these rules don’t work, use the overriding premise and work out the oxidation numbers, i.e., the more electronegative element gets the electrons (or the negative oxidation number).
16.1.2: Balancing Redox Equations
Now we can use the oxidation numbers as discussed in the previous section to help us balance REDOX reactions. There are as many different methods of balancing redox equations as there are text books on the subject. Personally, I’ve used at least 4 different methods and I have my favorites. Herein, I will use the algebraic method we discussed earlier in the year to balance REDOX equations. Because of the peculiarities of REDOX, I will give you a set of rules to follow to guide you.
A Half-reaction Method for balancing REDOX equations.
- Assign ONs and determine which elements change
- Divide the reaction into half reactions using the elements which change as a guide.
- Add e– and H2O to both half reactions, and, in acid, add H+, and, in base, add OH–.
- Use the Algebraic Method to balance the two half-reactions. There are other methods you can use as well but we’re teaching this method, which will work for all cases.
- At this stage, you have two balanced half-reactions. These are useful if you’re doing electrochemistry. If you need to get the overall reaction, you can do so by adding the half-reactions together such that the electrons are canceled out.
Now let’s try a few examples.
Sodium nitrate reacts with zinc in sodium hydroxide solution to give ammonia and the tetrahydroxozinc(II) ion, Zn(OH)42– . We have:
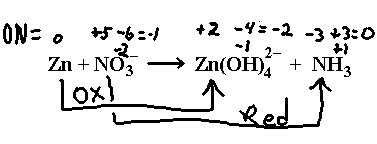
Break this up into half reactions according to the arrows drawn here.
![]()
Now add e–, H2O, and OH– (in base).
![]()
Use algebraic method to balance.
Oxidation:
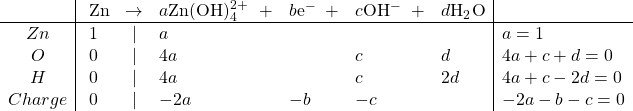
Solving, we get ![]()
So the balanced equation, after moving the hydroxide to the reactant side, because of the negative value of c, is: ![]()
Reduction:
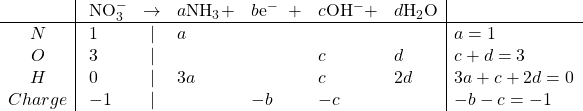
Solving: ![]()
Balanced: ![]()
Both these half reactions are balanced. To get the overall reaction, we need to add up these in a way that there are exactly as many electrons in the products as in the reactants side so that they cancel. We multiply the oxidation reaction by 4 to do this.
![Rendered by QuickLaTeX.com \begin{array}{rrcl} Oxidation: & 4\times \left[\mathrm{Zn + 4\;OH^- }& \rightarrow & \mathrm{Zn(OH)_4^{2-} + 2\; e^-}\right]] \\ Reduction: & \mathrm{NO_3^- + 6\; H_2O + 8 e^- }& \rightarrow & \mathrm{NH_3 + 9\;OH^- }\\ \hline Overall: & \mathrm{4\;Zn + NO_3^- + 6\; H_2O + 7\; OH^- }& \rightarrow &\mathrm{4\; Zn(OH)_4^{2-} + NH_3}\\ \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-197a7533f97b883ea62b2d4501c212cf_l3.png)
Now check the balancing to ensure both mass balance and charge balance is correct.
Another example:
Copper reacts with dilute nitric acid to give nitrogen monoxide NO.
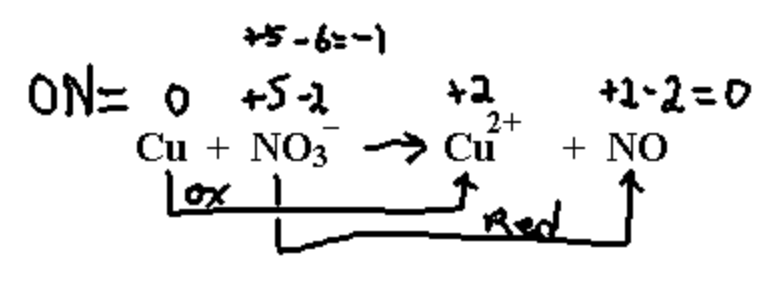
Notice that the ON for nitrogen in NO3– is an extremely unlikely +5. This could never be the actual charge on the nitrogen in any real compound (convincing evidence that oxidation numbers don’t represent reality very well).
We have the following two half reactions (use the chemicals joined by the arrows):
![]()
Now add e–, H2O, and H+ (in acid).
![]()
Use algebraic method to balance.
Oxidation:
* The copper oxidation was trivial. we already solved it by just adding two electrons. No need to do anything more complicated.
Reduction:
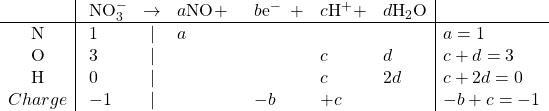
Solving: ![]()
Balanced: ![]()
Both these half reactions are balanced. To get the overall reaction, we need to add these together such that the electrons are canceled. That means 3x the oxidation reaction plus 2x the reduction:
![Rendered by QuickLaTeX.com \begin{array}{rrrcl} Oxidation: & 3\times [&\mathrm{Cu} & \rightarrow & \mathrm{Cu^{2+} + 2\; e^-}] \\ Reduction: & 2\times [&\mathrm{NO_3^- + 4\;H^+ + 3\;e^-} & \rightarrow & \mathrm{NO + 2\ H_2O}] \\ \hline Overall: && 3 \;\mathrm{Cu + 2\; NO_3^- + 8\; H^+}& \rightarrow & \mathrm{2\; NO + 4\ H_2O + 3\;Cu^{2+}}\\ \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c34cf5d39ff65b14cb7136e8c1041b5d_l3.png)
Now check the balancing to ensure both mass balance and charge balance is correct.
16.2: Introduction to Electrochemistry
Electrochemistry is the study of interchange of chemical and electrical energy.
Oxidation/Reduction involves the exchange of electrons from one chemical species to another. Normally, this is done when the two chemicals contact each other in the activated complex (when two species bump into each other in solution for example).
We are interested in separating the chemical species such that the electrons transfer via an external circuit. That way, we can measure the electrochemical effects.
To properly understand the connection between the redox reaction and the electricity, we should balance the overall redox reaction using a half-reaction method such as the one described in the previous section of these notes. We can set up the physical reaction vessel such that the chemicals from one half reaction are separated from those of the second half reaction. For reaction to occur, we still need to connect the solutions to complete the circuit. This is done by attaching wires between electrodes in the two half cells and by connecting the solutions of the two half cells via a salt bridge or by some other device such as a semi-permeable membrane.
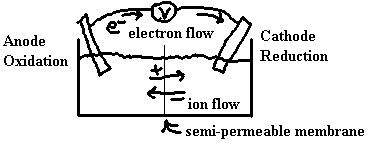
In general, such a cell is called an electrochemical cell. These cells could be used in one of two types of situations:
- The chemical reaction is spontaneous and produces electricity.
This is called a voltaic cell or a galvanic cell. - The chemical reaction is non-spontaneous and is forced by electricity from an external source.
This kind of cell is called an electrolysis cell.
We will look at the first situation first.
16.3: Galvanic or Voltaic cells
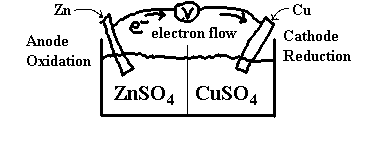
Consider a piece of zinc foil placed in a beaker of copper sulphate. The copper sulphate solution is blue because of the presence of the Cu2+ ions. When the zinc is added, the solution changes to colourless and the zinc metal is dissolved and replaced by a reddish orange powder. The colourless solution no longer has Cu2+ in it and the reddish orange powder is Cu(s). The Zn(s) is dissolved and is now Zn2+. [I know this because of my vast knowledge of chemistry ;-)]
If we write an overall reaction for this process, we get:
Zn + Cu2+ → Zn2+ + Cu. This doesn’t help us in our quest for electrochemistry knowledge. Let’s rewrite this in half-reaction form.
Zn → Zn2+ + 2e–
Cu2+ + 2e– → Cu
Now, we can set up two half cells, one with a zinc electrode in a Zn2+ solution (say ZnSO4) and the other with a copper electrode in a Cu2+ solution (say CuSO4) as follows.
The centre line in the diagram, recall, is either a semi-permeable membrane or a salt bridge.
Now, at the anode, we have the reaction
Zn(s) → Zn2+(aq) + 2e–(aq)
and at the cathode, we have
Cu2+(aq) + 2e–(aq) → Cu(s)
Electrons pass through the wires and SO42– pass through the membrane to keep the solutions neutral.
16.3.1: Cell Potentials
Electrons from solution are pushed onto the anode, around the external circuit and onto the cathode where they are pulled out into the solution. Electrons always flow from anode to cathode.
That’s one way of thinking of the electrical circuit part of the electrochemical cell. The electrons pushed around the external circuit can do work (run a motor, illuminate a light bulb, etc.). The amount of work possible is a function of both the voltage (potential) and of the current (number of electrons) in the circuit.
Pushing one Coulomb of charge around a circuit at a potential of 1 Volt does One Joule of work. OR, mathematically, 1J = 1V × 1C.
The cell potential (voltage of the cell) depends on the chemicals used. For example, the chemicals in dry-cells (batteries) are such that the potential is always about 1.5 V. This has become a standard and is now a limiting factor in deciding which chemicals can be used to create a battery.
The cell potential is given a symbol of Ecell. If all chemicals are at activity of 1 (conc. = 1 M, p = 1 bar) then the cell potential is the standard cell potential and is given as E°cell.
Any redox reaction has the potential (pun) to be used in an electrochemical cell. We merely need to be able to divide the oxidizing and reducing agents into two half cells (half reactions).
Take for example, the reaction of zinc metal dissolving in hydrochloric acid. The reaction is:
Zn(s) + 2H+(aq) → Zn2+(aq) + H2(g)
We need to separate the zinc from the hydrogen. We can use zinc as an electrode but what about the hydrogen.
In this case, we need to set up a special electrode, which allows H2 gas molecules to interact directly with H+ dissolved in water and with the electrons from the external circuit simultaneously. Such a system is pictured below.
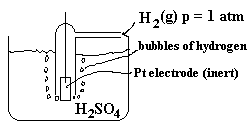
A blow-up of the surface of the platinum electrode is shown below so the location of reaction can be better understood.
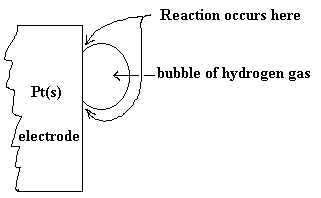
The other half-cell would look much like that pictured in a previous diagram. The whole cell diagram, of course would include the external part of the circuit and the salt bridge or membrane to complete the circuit. We can abbreviate this diagram as follows:
Zn(s)/ZnSO4(aq)//H2SO4(aq)/H2(g),Pt(s)
[Anode // Cathode]
Where the single slash mark / represents the boundary between solution and electrode and the double slash // represents the salt bridge or semi-permeable membrane. The external circuit, of course, joins the two electrodes (solid) and is not explicitly shown here.
The overall cell voltage can be summed from the half-cell potentials of the oxidation and of the reduction reactions.
Ecell = ERed + Eox.
16.3.2: Standard Reduction Potentials
As before, we wish to tabulate thermodynamic data in some useable way. We define a standard set of conditions under which all half-reactions can theoretically operate and we tabulate the half-cell potentials for the reactions under standard conditions. Since the potential of an oxidation reaction (loose electron) is merely the negative of the potential for a reduction reaction (gain electron), we choose to tabulate only the reduction half-reactions. Any oxidation half reactions are merely the reverse of the tabulated reduction reaction and the oxidation potential is the negative of the tabulate reduction potential.
Table of Select standard reduction potentials.
| reduction | ||
|---|---|---|
| 1 | O2 + 4H+ + 4e− |
+1.229 |
| 2 | Ag+ + e− |
+0.7996 |
| 3 | Cu2+ + 2 e− |
+0.3419 |
| 4 | Fe2+ + 2 e− |
−0.447 |
| 5 | Zn2+ + 2 e− |
−0.7628 |
| 6 | 2H2O + 2e− |
−0.83 |
| 7 | Na+ + e− |
−2.71 |
You can find a more complete table of standard reduction potentials in Appendix 4.
Let’s look at this small reduction potential table and see if we can use it to explain certain experimentally observable properties of matter. First off, I should point out that the more positive reduction potentials refer to more spontaneous reduction reactions.
The first reaction in this mini-table shows the reduction of oxygen. This is higher in the table than many other things. That makes sense since we know that oxygen is a good oxidizing agent (it makes other things oxidize while it itself is reduced).
We can see that water can be both oxidized (#-1) and reduced (#6). It is oxidized to oxygen and reduced to hydrogen. These two reactions, in fact, serve as a set of boundaries for aqueous solutions. Any materials harder to oxidize than water will not oxidize since the water will. Similarly, any materials harder to reduce than water will never reduce (in water). For example, sodium ions will never reduce to sodium metal in the presence of water since the water will reduce first. In fact, sodium metal in water will spontaneously (explosively) oxidize to Na+ ions and the water will reduce to hydrogen gas and leave a basic solution (equation 6). The overall reaction for this process is the sum (#6) – 2×(#7).
| NOTE: when we add half-cells, their potentials are strictly additive. We don’t multiply or divide by any factors even though we do so to the stoichiometric coefficients of the equations in order to balance the overall equation. Potentials don’t depend on the total amount or size of the cell, just the concentrations. You already know this. If you buy a AA cell or a D cell, their voltages are both 1.5V. However, their capacity to do work is not the same. |
2Na + 2 H2O → 2Na+ + H2 + 2OH–
Thus, the overall standard cell potential for this reaction is
![]() (reverse reaction => change sign) = 1.88 V.
(reverse reaction => change sign) = 1.88 V.
Positive cell potential means spontaneous reaction.
When pairing up metals, we know that zinc will dissolve in a copper (II) solution. Here we see that the copper (II) (#3) is easier to reduce than the zinc (II) (#5).
| A few years ago, a city I was living in experienced a number of very serious water main breaks on sections of pipe that had been recently replaced. The City engineer was fired. His only defense was “How was I to know that brass fittings (mostly copper) on cast iron pipes would corrode so fast.” It was front page news on the City paper. Was the city justified in firing him? Can you explain their reasoning for calling him incompetent? |
16.4: Gibbs Energy and Cell potential
Let’s now relate the electrochemistry ideas we’ve explored with the thermodynamic parameter called Gibbs’ Energy, ![]() .
.
We saw,
![]() (work = – charge times potential),
(work = – charge times potential),
where ![]() is the charge and can be defined as
is the charge and can be defined as ![]() where
where ![]() is the Faraday constant (96485 C/mol), named after Michael Faraday.
is the Faraday constant (96485 C/mol), named after Michael Faraday.
In our case, we’re interested in the maximum work since this can be related to the thermodynamic parameter ![]() .
.
Thus, for the case where the work is done infinitely slowly (chemical system is always at equilibrium with the electrodes, electrical resistance is zero since current is essentially zero, etc…) we have ![]() where
where ![]() for standard conditions is simply
for standard conditions is simply ![]() as calculated from the tabulated half-cell potentials. Take for example, a cell with a maximum cell potential of 2.50 V. If 1.33 mol of e- passes through the cell at an average potential
as calculated from the tabulated half-cell potentials. Take for example, a cell with a maximum cell potential of 2.50 V. If 1.33 mol of e- passes through the cell at an average potential ![]() = 2.10 V. What is the efficiency?
= 2.10 V. What is the efficiency?
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} w &=& -Q E\\ &=& -nFE\\ &=& 1.33\textrm{ mol} \times 96485\textrm{ C/mol} \times 2.10\textrm{ V (V = J/C)}\\ w &=& -2.69 \times 10^5\textrm{ J} = -269\textrm{ kJ}\\ \\ w_{max} &=& -nFE_{max}\\ &=& 1.33\textrm{ mol} \times 96485\textrm{ C/mol} \times 2.50\textrm{ V}\\ &=& -321\textrm{ kJ}\\ \textrm{efficiency} &=& \frac{w}{w_{max}} \times 100\% = \frac{-269}{-321} \times 100\% = 83.8 \%\\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dd3ec85b5e9527dbcd90dfb368181af0_l3.png)
Of course, since ![]() is only achievable if the work is done reversibly (infinitely slowly), we can never reach 100% efficiency in any system in the real world.
is only achievable if the work is done reversibly (infinitely slowly), we can never reach 100% efficiency in any system in the real world.
We already have seen that ![]() is a measure of the maximum work obtainable from a system. Thus,
is a measure of the maximum work obtainable from a system. Thus,
![]()
![]()
![]()
In this case, the potential is the cell potential ![]() .
.
![]()
Thus, we now have a link between free-energy, equilibrium and electrochemical thermodynamic parameters.
Example:
Is Fe2+ spontaneously oxidized by the oxygen of the air in acidic solution? Calculate ![]() and
and ![]() .
.
Two half-reactions can be determined by looking in the table of standard reduction potentials.
![Rendered by QuickLaTeX.com \begin{array}{crclc} \mathrm{Oxidation\; of\; iron} & \mathrm{4\;[Fe^{2+}}&\rightarrow&\mathrm{Fe^{3+} + e^-]}&-E^\circ_{ox} = -0.77 V\\ \mathrm{Reduction\;of\;O_2} & \mathrm{O_2 + 4H^+ + 4e^-}&\rightarrow&\mathrm{2H_2O}& E^\circ_{red} = 1.23 V\\ \hline \mathrm{Overall}&\mathrm{4Fe^{2+} + O_2 + 4H^+}&\rightarrow&\mathrm{4Fe^{3+} + 2H_2O}& E^\circ_{cell} = 0.46\textrm{ V} \\ &\multicolumn{3}{1}{ n = \textrm{4 mol Electrons/mol equation)}}&\textrm{Positive means spontaneous}\rightarrow \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c5f95117dd8a3b4d76a382ec47288589_l3.png)
So now we use the calculated reduction potential to find the Gibbs energy change.
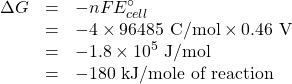
Now we find ![]()
SUMMARY
![Rendered by QuickLaTeX.com \[\begin{array}{|c|c|c|c|} \hline \textrm{Gibbs} & \textrm{Q vs. K} & \textrm{Cell potentials} & \textrm{Spontaneous direction} \\ \hline \Delta G<0 & Q < K & E_{cell} > 0 & \rightarrow \\ \hline \Delta G=0 & Q = K & E_{cell} = 0 & \rightleftarrows \\ \hline \Delta G>0 & Q > K & E_{cell} < 0 & \leftarrow \\ \hline \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a86050d4d202a1a6a4cd11bbd8b50352_l3.png)
16.5: Non-Standard Conditions: Nernst Equation
Consider the following set of half-reactions
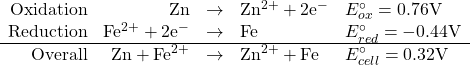
This is valid only if all species have concentrations of 1 M.
What if not all the species are at Standard Conditions?
Le Châtelier’s principle gives us some ideas. Look at the overall reaction. Consider the reaction to be at equilibrium (Ecell = 0 V). If we add more Fe2+ to the reaction mixture, The equilibrium will shift to the right to use up the excess Fe2+. This will, of course cause a positive cell potential to be measurable.
Conversely, if we removed Fe2+ from the reaction mixture, the equilibrium would shift to the left to try to replace some of the missing Fe2+. This would result in a measurable negative potential (reaction goes left).
If the reaction were not at equilibrium then these preceding two changes would be additive to the measured voltage (say standard voltage). So, if we add Fe2+ to a mixture at Standard Conditions, then the voltage would be more positive and if we removed some Fe2+ from a mixture at Standard Conditions the measured voltage would be lower (less positive).
The reverse results would be found for addition or removal of Zn2+ (a product). More Zn2+ would give a lower positive potential and vice versa.
Now we try to quantify the previous hand-waving discussion.
Recall the relation: ![]() (for non-standard conditions)
(for non-standard conditions)
Substitute the new definition of ΔG and we get
![]()
(This is called the Nernst Equation).
Thus, we can calculate the cell potential of any cell, given only the initial conditions (to calculate ![]() ) and the reduction potentials (to calculate
) and the reduction potentials (to calculate ![]() ).
).
Now, looking back at the reaction cell discussed at the beginning of this section we can calculate the voltage for the situation where the concentrations are not standard. For example, consider [Fe2+] = 0.10 M and [Zn2+] = 1.9 M.
For this reaction, we also know that there are two electrons transferred for each equation (![]() ).
).
![Rendered by QuickLaTeX.com \begin{array}{rcl} E &=&E^\circ - \frac{RT}{nF}\times ln \left(\frac{\mathrm{[Zn^{2+}]}}{\mathrm{[Fe^{2+}]}}\right)\\ \\ &=&0.32\textrm{ V} - \frac{8.3145\textrm{ J/mol K}\times 298.15\textrm{ K}}{2\times96485\textrm{C/mol}}\times ln\frac{1.9}{0.10}\\ \\ &=&0.28\textrm V} \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2d2b1e19605e6b7b6aa58153dcbb120a_l3.png)
Although the reaction is 90% complete (from Standard Conditions initial) the cell potential has only dropped by a small amount (0.04 V). This is normal. For example, the batteries in your flashlight will put out almost full voltage until the last traces of chemical are almost used up at which point the voltage will drop off rather sharply. This is an especially useful characteristic of cells powering electronic equipment, (like a calculator or CD player, etc.) which require a certain minimum (and dependable) voltage to operate successfully.
We can also use the Nernst equation to calculate such things as equilibrium constants.
At equilibrium, ![]() and
and ![]() so the Nernst equation becomes
so the Nernst equation becomes
![]()
or
![]()
Example:
What is the equilibrium constant for the reaction of copper metal with bromine to form copper(II) ions and bromide ions in aqueous solution at 25℃?
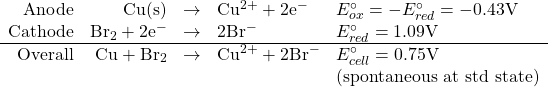
![]()
so
![]()
Example:
What is the value of the solubility product constant for AgCl?
We could calculate this by breaking the overall Ksp reaction into a series of redox reactions as follows:
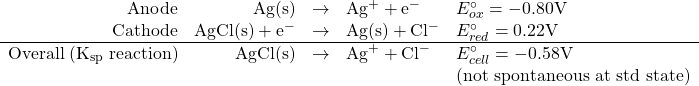
![]()
so
![]()
Ion Concentrations can also be calculated…
Consider the Platinum-Hydrogen electrode coupled with a copper/copper(II) electrode.
The overall reaction is ![]()
The Nernst equation is
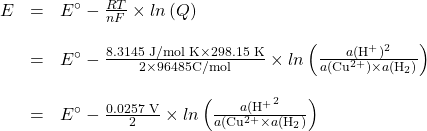
since
![]()
You will often see the Nurnst equation written this way, with the constant .0257 rather than the fraction ![]() . As you can see, at a temperature of 298.15K,
. As you can see, at a temperature of 298.15K, ![]() , so this is merely a shortcut version of the full equation. But, beware! The shortcut equation only works at 25 ℃.
, so this is merely a shortcut version of the full equation. But, beware! The shortcut equation only works at 25 ℃.
If [Cu2+] = 1 M and ![]() (H2) = 1 bar (both their activities are 1) then
(H2) = 1 bar (both their activities are 1) then
![]() V
V ![]() [H+]
[H+]
(Note: ![]() and
and ![]() )
)
![]() V (
V (![]() [H+])
[H+])
![]() V ×
V × ![]() .
.
We see here that the cell potential is a function of ![]() . The probes in
. The probes in ![]() meters are set up this way. A complete electrochemical cell is contained within the probe casing. All chemicals are at standard conditions and a porous glass membrane allows only H+ ions to pass through. The diagram of the set-up is given here.
meters are set up this way. A complete electrochemical cell is contained within the probe casing. All chemicals are at standard conditions and a porous glass membrane allows only H+ ions to pass through. The diagram of the set-up is given here.
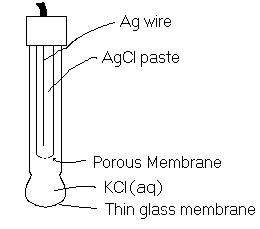
16.5.1: Concentration cells
A concentration cell is one in which the half-reactions in the two half cells are identical but the concentration of the ions is different. In this case, the reduction and the oxidation half reaction are identical. Take for example a concentration cell where both half cells have an iron electrode in a Fe2+ solution. We would have the following:
Consider the following set of half-reactions
If all concentrations are identical (or if they are all standard) then obviously the cell voltage is zero. If, however there is a different concentration on one half cell than on the other one, we could use the Nernst equation to calculate, for example the cell potential.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} E &=& E^\circ - \frac{RT}{nF} ln\;Q \;\;\;^*\\ \\ E &=& -\frac{RT}{nF} \;ln\;Q\;\;\;^{**} \\ \\ E &=& -\frac{RT}{nF}\;ln \;a(Fe^{2+})_2\;\;\;^{***} \end{array} \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-81df67f907428526d771b64e9d247bfa_l3.png)
* Note: ![]() where 1 and 2 refer to the two half cells. and
where 1 and 2 refer to the two half cells. and ![]()
** Normally, we set the concentration of half-cell 1 to be fixed (at say, activity=1) and vary the activity of the Fe2+ in half-cell 2.}
*** assuming we set activity in cell 1 = 1}
Half-cell calculations
The Nernst equation can also be used to calculate half-cell potentials. In this case, ![]() is simply the ratio of ions of the half-cell equation rather than the full-cell and the value for
is simply the ratio of ions of the half-cell equation rather than the full-cell and the value for ![]() is that of the half-cell. No other changes to the equation are made.
is that of the half-cell. No other changes to the equation are made.
For example, Consider the iron to iron(II) half reaction.
![]()
This is written here as an oxidation so the cell potential is
![]()
Now, we can calculate the half-cell potential for such a system but where the concentration of the iron(II) ion is not standard (≠ 1 mol/L; say, 0.13 mol/L). We just use the Nernst equation where
![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rl} E &= E^\circ - \frac{RT}{nF}ln\mathrm{[Fe^{2+}]}\\ \\ &= 0.433 - \frac{8.314 \times 298.15}{2 \times 96485} ln [0.13]\\ \\ &= 0.469 V\end{array} \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5a5551d12b0b4efe590ff0bc775759f1_l3.png)
Batteries
There are three classes of batteries:
Primary Cells
Chemical reaction occurs irreversibly. The battery cannot be recharged. This can happen for several reasons, including the chemical properties and the design of the cell. Examples include standard Alkali batteries or their less common precursors the carbon/zinc battery. Leclanché cell (improperly called Zinc-Carbon dry cell)
This is the common dry-cell available in most stores that we use to power toys and flashlights. These involve a zinc casing (anode) and a carbon rod in the centre (cathode) with a paste of MnO2, NH4Cl, ZnCl2 and graphite.
The reactions involved are
Notice that the reactant concentrations will diminish and the product concentrations will build up in this type of cell and cause the overall cell potential to drop, according to the Nernst equation.
Alkaline cell (alkaline meaning basic)
In the alkaline cell, the product of the cathode reaction is used up again in the anode reaction, no build up of products means the voltage drops (as water is used up) more slowly than the previous cell. Since the cell voltage is also about 1.5 V, this alkaline dry cell can be used in the same devices as the normal dry cell. Notice, the only real difference between these is the fact that the reaction in this case occurs in a basic medium.

Ruben-Mallory (mercury) cell
This type of cell is used in application where the cell potential must remain very constant over the life of the battery (commonly computers and watches, etc). The products and reactants are all pure substances (standard state). Since the voltages of these cells are not the same as the previous two, this type of battery is not interchangeable with the first two types.

Notice that the Ruben-Mallory cell will always have almost all it’s products and reactants at activity = 1. They are either solid or pure liquid. The amounts will change as the reaction proceeds but their activities remain constant. This means that the voltages will remain constant until the end, when one or the other of the reactants is completely used up. This kind of cell was first used for devices where a stable voltage was critical, such as a hearing aid.
Secondary Cells
Chemical reaction is reversible. The battery can be recharged. Examples include NiCd batteries and Lead/acid batteries found in cars. These are also called storage cells or rechargeable cells. In theory, alkaline batteries can also be recharged, the process, however is dangerous and can lead to explosions if not done with the proper equipment. Similarly, lead/acid car batteries can explode if they are charged too fast but for a different reason.Lead/acid battery has an overall reaction of
Pb(s) + PbO2(s) + 4H+(aq) + 2SO42- → 2PbSO4(s) + 2H2O(l)
with a cell voltage of just over 2 V. Hence, six cells in series will make a battery of cells with a combined voltage of 6×2V ~ 12 V. (actually closer to 13 V).
Nickel/Cadmium batteries have reactions

We see that none of the reactants or products are in solution so the voltage will remain very constant during the discharge period. Unfortunately, the cell voltage is lower than standard dry cells and are not always interchangeable. Additionally, Cadmium is a toxic heavy metal. The use of NiCad batters has been greatly reduced in recent years. with the advent of better rechargeable technology that uses less toxic chemicals.
Lithium ion batteries is one example of a more recent, less toxic rechargeable type cell in use. The electrodes both use a solid matrix with lithium ions embedded. The voltage arises from the different stability of the lithium ions in the two different solid electrodes. Hence, the name “lithium ion” battery. The exact voltage of the system will depend on the particular matrix material of the cathode (the anode is typically graphite) and its crystal structure.

There are actually several kinds of batteries with the name “lithium ion”, This is just one example. In this example, calcium oxide and graphite represent the solid cathode and anode, respectively. The lithium ion moves back and forth between the cobalt oxide and the graphite electrodes as the battery discharges and charges. The process of moving an ion into a solid is insertion (aka intercalation) and moving the ion out of a solid is called extraction (aka deintercalation). A major drawback to lithium ion batters is their tendency to be severely damaged if they are overcharged, either at too high a voltage or too high a rate. Careful electronic control of the charging process is required to avoid an explosion and fire hazard. Most of our modern electronics and even many Electric vehicles use some form of lithium ion battery system.
Fuel Cells
Reactants are flowed through the cell. This is an irreversible reaction but by refilling the reservoir of fuel the cell can be reused. The ISS International Space Station uses this type of battery to run much of its electrical equipment. Hydrogen powered vehicles also use fuel cells, where Hydrogen is the fuel that oxidizes with oxygen in the air to make water as the product. Very clean, as long as the hydrogen production itself was clean.
16.6: Electrolysis and Electrolytic Cells
We’ve seen how spontaneous reactions can be harnessed to produce electricity. In electrolytic cells, electricity is used to force non-spontaneous reactions to proceed. Electrolysis is used to prepare certain compounds and metals. Products of electrolysis are found in every day life: Chrome plated bumpers, Silver and gold plating on some inexpensive jewelry, among other things.
In setting up an electrolysis cell, we must take into account all possible reactions and make sure the conditions are set so that the desired reaction occurs. We will do this at first by using only inert electrodes and then by using pure electrolyte liquids rather than aqueous (or other) solutions.
We will use a non-aqueous system such as molten NaCl as our medium, and non reactive electrodes like platinum. We can successfully separate out pure Na. Consider the following electrolytic cell.
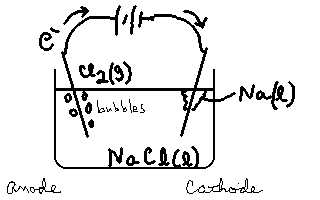
This is a very important method of producing sodium metal. At the anode, Cl2 is evolved in the reaction
2Cl– → Cl2(g)+ 2e–.
At the Cathode, the molten sodium ions are converted to sodium metal (liquid at these temperatures) in the reaction
Na+ + e– → Na(![]() ).
).
Alkali earth metals which are also highly reactive can be prepared using electrolysis of molten chloride salts as in the reaction MgCl(![]() ) → Mg(
) → Mg(![]() ) + Cl2(g)
) + Cl2(g)
Other metals which are not quite as reactive as the above two families but are sufficiently reactive that they cannot be produced in an aqueous cell can be produced this way. Aluminum is one such metal.
The Hall process invented before the turn of the century allowed for the production of aluminum on an industrial scale.
A molten mixture of aluminum ore (Al2O3) and cryolite (Na+)3(AlF6–)(l). The cryolite is the solvent and it is used because it has a lower melting point than pure Al2O3. A carbon electrode acts as the anode and aluminum forms the cathode such that the following reactions occur:
Al3+ + 3e– → Al(![]() )
)
C(s) + 2O2– → CO2(g) + 4e–
This process needs lots of electricity per kg of aluminum so you will most commonly find aluminum production plants very close to electric power stations to reduce the cost of electricity.
16.6.1: Quantitative Aspects of Electrolysis:
Consider the reaction in the molten NaCl electrolysis cell.
| 2Cl– → Cl2(g) + 2e–. | 2 moles of electrons per mole of Cl2(g) |
| Na+ + e– → Na( |
1 mole of electrons per mole of Na metal |
Recall that the charge on the electron is ![]() where
where ![]() is the Faraday constant (96485 C/mol), named after Michael Faraday.
is the Faraday constant (96485 C/mol), named after Michael Faraday.
Thus, to produce one mole (23 g) of sodium, we need
![]() = 1×96485 C = 96500 C.
= 1×96485 C = 96500 C.
To produce one mole (70.9 g) of chlorine gas, we need
2×96500 = 1,930,000 C.
Current is defined as the amount of charge passing a point in a circuit in one second.
![]() The units are 1 Ampere = 1 Coulomb/second (1A = 1C/s).
The units are 1 Ampere = 1 Coulomb/second (1A = 1C/s).
Now, if we have a current of 50.0 A passing through an NaCl(l) electrolysis cell in 1 hour, how much sodium and chlorine will we produce?
50.0 A × 3600 s = 180,000 C (NOTE: 1As = 1C)
![]() = 180,000/96,485 = 1.87 mol e–
= 180,000/96,485 = 1.87 mol e–

It takes lots of current to produce very little sodium and chlorine.
We can do other types of calculations similar to this.
What mass of aluminum will be produced in 1.00 h by electrolysis of Molten AlCl3 using a current of 10.0 A?
![]()
It takes three moles of electrons for every mole of Aluminum. So…
![]()
What volume of Cl2(g) at STP (0°C, 1 atm) will be produced by a current of 20.0 A in 2.00 h in the same cell as used in the previous example?
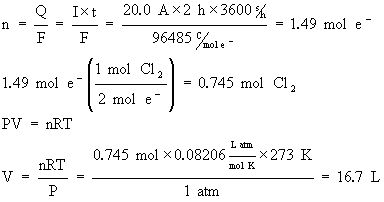 Note that in this problem, we used
Note that in this problem, we used
R=0.08206 Latm/mol K.
This was to facilitate the conversion to volume. You could have also used the more standard value of R=8.314 J/mol K but conversion to volume would have involved one more step of calculations.
If we had tried to electrolyse sodium Chloride in water, we would need to consider not only the Na+ and Cl- as possible reactants but also the water. We can never produce sodium in aqueous solution, because it will spontaneously react with the water to produce Na+(aq). Whether we tried to produce sodium metal either chemically or electrolytically, the chance of success would be equally bad. Thus, at the cathode of an aqueous NaCl cell, we would get the reduction of water happening
2H2O + 2e– → H2 + 2OH– ![]() = –0.83 V
= –0.83 V
rather than the reduction of the sodium
Na+ + e– → Na ![]() = –2.71 V
= –2.71 V
Notice that the reduction potential for the water reduction is a lot more positive than that for the sodium. This is a way we can look up reduction potentials and tell what will happen in our solution before hand.
Looking at the two possible reactions at the anode of the NaCl(aq) cell, we see that the Cl– and the H2O are both candidates for oxidation. The two possible half-reactions are:
2H2O → O2 + 4H+ + 4e– ![]() = –
= –![]() = –1.23
= –1.23
2Cl– → Cl2 + 2e– ![]() = –
= –![]() = –1.36
= –1.36
Since the water has a more positive oxidation potential than the chlorine reaction, it should be oxidized more readily. There is a complication, however. The water oxidation requires a considerable over-voltage (extra voltage) to make the reaction rate appreciable. Since the two possible reactions are quite close in potentials the extra voltage can quickly be sufficient to cause the chlorine oxidation to occur. Since this latter reaction is quite rapid in comparison to the water oxygen one, it will dominate at only slightly elevated voltages.
If we had used Na2SO4 rather than NaCl as the electrolyte, then the anode reaction would have been the water one since SO42– is very difficult to oxidize (very negative oxidation potential in comparison to water).
16.6.2: Electrolytic Purification of Metals
Consider the electrolysis of Copper(II)sulfate solution.
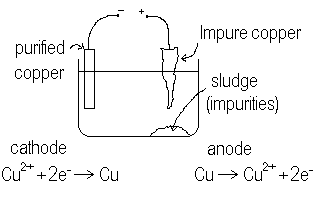
We find O2 produced at the anode and copper solid deposited at the cathode. This means, as we saw before that the water is more easily oxidized (to oxygen) than are the sulphate ions while the copper(II) ions are more easily reduced (to copper metal) than is water (to hydrogen). Hence, it is quite easy to set up an electrolytic purification process for copper metal. Unlike aluminum, where we needed molten baths of aluminum ore, we need only dissolve the copper in a water solution and then electrolyze it out as copper metal. If we do a crude separation chemically of the copper from the ore, we can use this impure copper as the anode and use pure copper as the cathode. Then, we will electrolyze copper ions off of the impure copper anode and then reduce them onto the pure cathode in the same solution. Impurities in the anode would merely settle to the bottom of the cell to be disposed of. We need to take care to adjust the voltage so that only the copper is oxidized from the anode and not some of the impurities. This done, we can successfully purify copper using electrolysis. The slower we take the reaction (less over voltage) the more pure will be the copper.
16.6.3: Products of Electrolysis
We’ve seen that the particular product of electrolysis we see at the electrodes depends on the ease of production of that particular species. There are three factors that determine product that we will find in any given electrolysis cell: the electrode material, the solvent and the electrolyte. Often, we use inert electrodes and/or pure liquids to help alleviate some of the complications from competing chemistry, other times, we must simply carefully adjust conditions (concentrations and voltages) to ensure that the desired product is achieved.
| @ Cathode
Reduction of substances most easily reduced will be the one observed. For example, Na+, Ca+, Al+ all have more negative reduction potentials than water so they will not be reduced in aqueous solutions On the other hand, Cr3+, Cu2+, Ag+ have reduction potentials more positive than that for water so they will be preferentially reduced at the cathode. @ Anode |
| Oxidation of substances most easily oxidized will be observed. For example, Br–, I– will be oxidized but F– and Mn2+ will not. (check reduction potentials) |
Complication: Cl– we’ve seen to be more easily oxidized than water even though it has an oxidation potential (negative of the reduction potential for Cl2) which is more negative than that for water. This is due to kinetics. The water reaction is quite slow and requires a large voltage to force it to proceed with any speed. The Cl– oxidizes to Cl2 much more rapidly and the over voltage we apply in an attempt to force the water to oxidize is sufficient to produce Cl2 which occurs faster.
Summary:
| Reaction involves | Anode | Cathode | |
|---|---|---|---|
| 1 | Electrolyte | Anions oxidized | Cations reduced |
| 2 | Solvent | Solvent oxidized | Solvent reduced |
| 3 | Electrode | Electrode oxidized | Electrode reduced |
16.7: Corrosion of metals
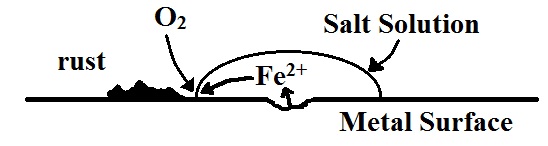
From the table of reduction potentials, we can see that oxygen from the air can be reduced to water and that the reduction potential for this half-reaction is very positive. More positive, in fact than that for most metal reduction process. This means that any metal in contact with oxygen from the air and in the presence of an electrolyte solution will oxidize. Since mining and production of metal is a fairly energy-intensive process, it is very useful to be able to find ways to reduce or eliminate the oxidation of these metals if at all possible. There are several ways to reduce oxidation of metals
Eliminate the oxygen/metal contact
This is achieved by coating the metal with some material that is impervious to either the oxygen or to any aqueous salts. This prevents the electrical circuit from being complete in the ‘electrochemical cell’ that is spontaneously set up at the point of rusting.
To protect the metal from corrosion, we can use several methods
Isolate the metal
- Paint the metal. This is a pure insulating technique and serves merely to keep the reacting species separated. Unfortunately any small scratch will allow the reaction to start up and may even accelerate the process.
- Oil the metal. (various rust-proofing companies use this technique). The unfortunate problem is that oil is a volatile liquid and eventually either runs off the surface or evaporates away, leaving the metal unprotected. Special surfactants can be added to the oil to make it cling to the metal surface and slow evaporation. You will find these surfactant agents in treatments such as RustCheck and Canadian Tire rust-proofing treatments. No matter, these treatments must be repeated regularly (yearly) to maintain protection.
- Anodize the metal: sometimes, the oxides of the metal are very stable and act to insulate the metal from the air. This is most obvious in copper roofing where the (orange) copper metal is quickly oxidized to the green oxide CuO. This oxide is quite stable and protects the underlying metal from further corrosion. This is useful in that small scratches quickly ‘seal themselves up’ with more oxide and the process is halted. Aluminum is often deliberately anodized in a controlled electrochemical cell to form an aluminum oxide coating that is relatively stable (in neutral solutions).
- Coat the metal with a material that oxidizes easier than the metal you wish to protect. For example, steel coated with zinc will not oxidize until first all the zinc is oxidized because the zinc will change the electrical potential of the steel and prevent it from being oxidized even if it is exposed to the air and water. This protection will last until the zinc is used up. at which time, the steel will start to oxidize.
Cathodic protection
- Use a sacrificial anode made of a material that oxidized easier than the metal you wish to protect. This is similar to coating the metal with the material (as in galvanized steel) but is simpler to do since it merely means attaching chunks of the anode material rather than going through a coating process.
Pipelines are often protected this way, the steel pipes are attached by a wire to a large block of zinc buried next to the pipeline in the ground. The zinc serves to electrically charge the steel changing its potential and thus reducing the amount of oxidation. - Electrically change the metal’s potential. Similar to the use of sacrificial anodes, this process involves attaching the negative pole of an electrical system to the metal we need to protect. In cars, for example, the negative pole of the battery is the ground. This serves to charge up the car and change it’s potential. Thus, the oxygen has to overcome both the iron’s reduction potential as well as the batteries artificial potential to force the reaction to happen. Cars would rust out far quicker it they were grounded positive since that, in effect, would serve to increase the rate of oxidation of the steel.