1 Review of Fundamentals
Michael Mombourquette
We are assuming the students all have the ability to manipulate equations (algebra) as well as performing calculations using equations. This unit should serve as a quick review of high school knowledge for most students. In addition, there are a few hints and techniques that may be new to you.
1.1: Dimensions and Units
Using units and dimensions as an integral part of problem solving is a very important strategy in solving problems. Many students seem to consider units to be nothing more than an add–on to the process of solving chemistry problems. A better way to think of units can come if you realize that dimensions and units can lead you to the solution for many problems. We will explore the basic concepts here and begin the development of skills necessary to aid in problem solving.
Units and dimensions don’t actually mean the same thing. A dimension represents a kind of measurable quantity. There are a limited number of basic measurable quantities in the world. They are listed here in this table:
| Dimensions | Short–Hand Notation |
| length
mass time electric current thermodynamic temperature amount of substance luminous intensity |
[L]
[m] [t] [i] [T] [n] [I] |
For each dimension, there are many possible units. We will tend to use the Systême Internationale (SI) units in this course (and other science courses) but other units of measure are sometimes encountered, especially in popular language or in older publications. An excellent web site on the SI system is found here. The following tables show multiple possible units for three basic measurables (dimensions), length, mass and time. The SI units are indicated with an asterisk.
| Dimension | Units | Abbreviation |
| length [L] | metres*
centimetres kilometre angstrom miles inches |
m
cm km Å=10–10 m mi in |
| Dimension | Units | Abbreviation |
| mass [m] | kilogram*
gram |
kg
g |
| Dimension | Units | Abbreviation |
| time [t] | second*
minute hour |
s
min h |
There are huge scale variations in the quantities that may be measured. We need to keep the ranges of the magnitudes in mind when we are working with numbers. It is always helpful for a student to recognize when an answer they calculate is outside of the range of possibilities, indicating they have likely made a mistake.
- length
- 10–15 m = size of an atom
- 10+25 m = size of the universe
- mass
- 10–30 kg = mass of e–
- 10+29 kg = mass of the universe
- time
- 10–23 s = molecular frequency
- 10+17 s = age of the universe
We should note that there is a common confusion between mass and weight. Mass is a basic measure of the quantity of material. The measured mass of an object does not change as it is moved from place to place. Weight, however is a derived quantity, defined as w = m×g (units include pound, ounce and Newton). The value ‘g‘ is the acceleration due to gravity and it’s magnitude depends on location. It is not the same at sea level as on a mountain top and is very small in free space. That is why the weight of an object changes as the object moves to regions with different gravities. Thus, weight is the force of gravity while mass is not a force! (Even though we sometimes use weight and mass interchangeably).
1.2: Scientific Notation
When we deal with the kinds of numbers that nature gives us, we need a more convenient way of expressing them than straight up algebraic notation. We use scientific notation to represent the scale of the number as a value and an order of magnitude (power of 10).
0.00…009109534 kg (mass of an electron, me)
[30 zero’s from bolded zero to bolded zero]
Better written as:
9.109534 × 10–31 kg
When we express a number in Scientific Notation, we must only show the significant digits in the number. Above, we have expressed the value of me to 7 sig. figs. We know that the last digit is uncertain but we don’t know by how much. To properly indicate the uncertainty in the numbers, we need to be able to incorporate the uncertainty into the number itself. One way is to simply indicate the limits of the range with a plus–or–minus symbol and a magnitude of the uncertainty to give the following notation:
9.109534 × 10–31 kg ± 0.000047×10–31kg.
The uncertainty is herein expressed via the second number with the plus–or–minus symbol. This indicates the centre of the range (the first number) and the size of the range from centre (the second number). The true value of the measured or calculated number is expected to lie somewhere within that range.
This method is awkward. A better way to express an uncertainty when using scientific notation is to incorporate the error as parenthetical digits at the end of the main number. Thus, the same uncertainty in the value of me can be written as follows:
9.109534(47) × 10–31 kg.
This now expresses the same number (range–centre and width) as before in a more compact way. Note that the uncertainty is knowable to more than one digit, indicating that we know the range within which the value of me lies relatively well. If we had rounded our uncertainty to a single digit the number would have to have been expressed as:
9.10953(5) × 10–31 kg.
This value is less certain than the previous one as the range of uncertainty is bigger so the former number would be a more accurate way to represent the value of the mass of the electron. In other words, yes, an uncertainty can have more than one “sig fig” in it.
1.3: Significant Figures
When we are reporting measured amounts, we need to specify the uncertainty limits of our number, i.e., we need to specify how accurately we know the value. Our calculator might be able to report to us 9 or 10 digits but perhaps only two of them have any meaning. When writing the number into a report, we should indicate this limit to the reader. The simplest method is to only write the “significant” figures, i.e., those digits in the number that are actually meaningful. The significant figures tends to give a poor estimate of the accuracy with which we know a value.
Take as an example, an individual walking the street with some money in his/her pocket. This individual has not kept exact track of his/her expenditures during the day but knows that there is about 15 dollars give or take maybe 50¢ (even this is only a guess in this example but is often calculated more accurately in scientific experiments). We write this amount in proper notation as $15.00+.5 or $15.0(5). In other words, we have defined a range of possible amounts that this person is carrying as being as low as $14.50 and as high as $15.50.
Now suppose this person notices a penny on the ground and picks it up. He/she now still has about $15. The penny is relatively insignificant since the known amount of money was uncertain to a larger amount than just 1¢. Mathematically, we could (erroneously) write this as $15.01(50). The range of possible amounts this number could represent is now $14.51 to 15.51 and is almost identical to the initial range of possible amount of money in his/her pocket. The problem here is the the limit of accuracy is only about 50 ¢ so we cannot even justify including the penny in the second range since we are so uncertain as to the actual size of the range. Hence, before and after picking up the penny, this person has about $15 give or take about 50 ¢ [$15.0(5)]. The penny was insignificant. While this example may seem a bit complex, most of the time we do calculations, we don’t actually calculate or propagate our errors (see your lab instructions for instructions on propagation of errors). We just keep track of significant figures. This method is easiest but also the least accurate way to keep track of our limits of uncertainty.
Let’s first try a few examples of simply counting significant figures in numbers to ensure we can properly determine them.
How many sig. figs?
| Number | # Sig. Figs | Number | # Sig. Figs |
| 2300 | 2 (unless there is a decimal point) | 0.0046 –> 4.6 × 10–3 | 2 |
| 2.3 × 103 | 2 | ||
| 2.30 × 103 | 3 | 0.00460 –> 4.60 × 10–3 | 3 |
| 2.300 × 103 | 4 | 0.004600 –> 4.600 × 10–3 | 4 |
Note that when we write the number in scientific notation that we must always write only the significant digits.
1.3.1: Keeping track of uncertainty
When combining numbers, we must also combine the uncertainties. There are several ways that we can determine the uncertainty in a final calculated number. Three key categories are listed here in order of diminishing accuracy. If you have a choice, always go with the higher priority method, even if it seems to overrule a lower priority method of determining the uncertainty in your calculated numbers.
- Statistical Methods: We can do the measurement and subsequent calculations repeatedly and then use statistical analysis to determine the standard error of the final number. This method is the most accurate method of determining the real (measured) uncertainty in any value that we must determine. Generally, the statistical uncertainty can be calculated easily for averages of measured or calculated values or for slopes and intercepts from multiple measured/calculated values. Spreadsheet programs like Excel and graphing programs like Logger Pro (used in our wet labs) will automatically give you the uncertainties in slopes and intercepts, which you can then use in method 2 to get to uncertainties in values you calculate using those slopes and intercepts. Your calculators will also give you uncertainties for things like means. Be sure to read the manual to determine how you might do this.
- Propagation of Errors: In cases where we cannot make repeated calculations or where we only have one set of data, we can estimate the uncertainty using the “propagation of errors” method. For this to work, we need to know the uncertainties in each datum we collect. This may mean we need to read the instrument documentation or labels to determine uncertainties. In other cases, we can estimate the uncertainty in measurements by simply taking 0.2 times the smallest division on the measuring device as the uncertainty in the measurement.
Once we have recorded all the individual uncertainties for our starting data, we then combining them as we move through the calculations to a final combined (but estimated) uncertainty. The uncertainty we obtain through “propagation of errors” methods will always give us an answer range that is larger than what we would get using method 1. One method for propagation of errors will be discussed below. - Significant figures: The simplest and least accurate method involves simply keeping track of the significant figures in our calculations. This is the least accurate way to get an answer range since we will not be sure if our range is too big or too small since we don’t really know the uncertainties to start with.
Keeping Track of Significant Figures
There are three basic rules for keeping track of significant figures (sig figs). The procedure we use depends on the calculation we are using.
1. Addition and Subtraction
When numbers are added or subtracted, we keep track of decimal places, not sig. figs. Thus, the answer has the same number of decimal places as the number with the lowest amount of decimal places. Of course, we must first re–write all the numbers to the same order of magnitude.
- Addition: 3.42×101 + 2.7×10–1 = 3.45×101
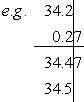 Here, we rewrote all numbers to 100 (standard notation). Here, we rewrote all numbers to 100 (standard notation). |
- Subtraction: 2.7×10–1 – 3.42×101 = –3.39×101
|
0.27 |
2. Multiplication and Division
In multiplication and division, we keep track of sig. figs and the answer must have only as many sig figs as the least accurately known number (least number of sig. figs).
- Multiplication: 3.42×101 × 2.7×10–1 = 9.234, rounded to 2 sig fig = 9.2
- Division: 3.42×101 ÷ 2.7×10–1 = 126.66666, rounded to 2 sig fig = 130 = 1.3×102
- In this case, we must convert to Scientific Notation because the number of sig figs in 130 is uncertain. It could be 2 or the author might have just forgotten the decimal point but really intended to show 3 sig figs.
If we are doing a more complex calculation that involved more than one type of calculation, we must carefully track the sig figs as we go. For example, consider the numeric problem below:
![]()
The calculated value for ![]() is 2.823625. But how many of these digits are significant? If we simply count the sig figs in the starting numbers, looking for the lowest count, we might think there should be 3 sig figs in this answer because the number 12.6 only has 3 sig figs. However, we have to keep track of the sig figs in the same order we do the math. The numerator of the fraction involves a subtraction and must be done before we can divide by the denominator and then multiply by the final number. So, we must do sig figs for the subtraction first. The numerator works out to 1.75 where the second decimal point is not actually significant. So the numerator has only two sig figs. Now, since the rest of the calculations involve only multiplication and divisions, we can count sig figs. Our answer must have only two sig figs because the numerator has two. Thus,
is 2.823625. But how many of these digits are significant? If we simply count the sig figs in the starting numbers, looking for the lowest count, we might think there should be 3 sig figs in this answer because the number 12.6 only has 3 sig figs. However, we have to keep track of the sig figs in the same order we do the math. The numerator of the fraction involves a subtraction and must be done before we can divide by the denominator and then multiply by the final number. So, we must do sig figs for the subtraction first. The numerator works out to 1.75 where the second decimal point is not actually significant. So the numerator has only two sig figs. Now, since the rest of the calculations involve only multiplication and divisions, we can count sig figs. Our answer must have only two sig figs because the numerator has two. Thus, ![]() . normally we would write only the 2.8 but Here, I am including a few insignificant digits as subscripts just in case we need to use that number in subsequent calculations. Never use rounded off numbers in your calculations if you can possibly avoid it.
. normally we would write only the 2.8 but Here, I am including a few insignificant digits as subscripts just in case we need to use that number in subsequent calculations. Never use rounded off numbers in your calculations if you can possibly avoid it.
If a further part to the question involves working out ![]() we will get the wrong answer if we use
we will get the wrong answer if we use ![]() rather than
rather than ![]() . The former will give a value
. The former will give a value ![]() whereas the correct answer is
whereas the correct answer is ![]() . RULE: never use rounded numbers in your calculations.
. RULE: never use rounded numbers in your calculations.
3. Logarithms
Logarithms are tricky since they are used to compress the scale of our numbers (see the section below). We don’t actually have an easy way to keep track of sig figs when we take the log or anti–log of a number. Let’s look at a few examples to get an idea how to handle logs.
| Log10 (1.34×103) | = Log10 1.34 | + Log10 1000 | |
| = 0.127105 | + 3 | =3.127 | |
| 3 decimal points here | this part is a whole number (order of magnitude), so infinite decimal points | total of 4 sig figs (we have “gained” a sig fig) |
When we took the logarithm of the number we seem to have gained a sig fig. What happened is that the Log base 10 of 1000 is exactly 3, infinite sig figs. thus, when we add 0.127 (3 decimal places) to the whole number 3, we get 3.127 with 3 decimal places but one more sig fig than our original number. So if we take a log of a number, the answer has as many decimal places as the original number had sig figs. We could gain one or more sig figs. For example, Log (1.34×1012) = 12.127, thus, we would gain two sig figs for this number.
On the other hand, if we do the reverse and take the antilog of 3.127, we will get back our original number 1.34 × 103, which obviously has only 3 sig figs. Thus, when we take the antilog of a number the answer has as many sig figs as the number of decimal places of the original. Thus, the antilog of 12.127 = 1.34×1012 has 3 sig figs. Logs and anti logs in base e (natural logs) work similarly but are not so cut and dried.
The general rule is be wary of the count of sig figs much once you do a log or antilog.
1.4: Dimensional Analysis
Most of the numbers we will work with or calculate will have units and most of these units will be derived units, not just the base units mentioned above. We saw one such derived unit for force = Mass * acceleration. By analyzing the dimensions involved, we can often determine what equation to use without resorting to looking up equations or memorizing equations.
Dimensional analysis affords us a way to analyze measured values and combine them to produce new values by merely watching that dimensions are properly considered. For example, the value called Area is a two dimensional value defined as length squared. We can quickly see that if we have two independent lengths (right angles to each other), we can multiply them to get a value with dimensionality of area.
We can thus, create our own formulae as needed without memorizing.
[L]2 = [L2] × area e.g. m2, in2
Similarly, Volume is a three–dimensional measurable as follows:
[L]3 = [L3] × volume e.g. cm3 (sometimes called cc = cubic centimeter × mL)
Speed, is a two dimensional measurable. The two dimensions are distance [L] and time [t] as follows
[L t–1] × speed e.g. m s–1 mph
Acceleration is a three dimensional measurable involving Length and time and time again.
[L t–2] × acceleration e.g. m s–2
Thus, going back to force, we see that it is a 4–dimensional measurable:
F = ma × [m] [L t–2] = [m L t–2]. The SI units for force are kg×m×s–2 × Newton, N.
![]()
1.4.1: Conversion Factors
We see that a value maybe expressed using different units but still have the same dimension.
In any equation, dimensions on both sides Must be the same. However, the units (and hence the number itself) may differ.
- e.g. 1 m = 100 cm
- e.g. 1 L–atm = 101.325 Joules
Whenever we see equalities, we can rewrite them into conversion factors by dividing one by the other. These conversion factors are extremely useful throughout your career in chemistry, etc. when the units we are given in a problem and the units we need for the answer are different. Conversion factors always have an magnitude of 1 (dimensionless but not unitless) and hence, they are used to convert from one unit to another without changing the magnitude or the dimensionality of the value we are representing. For example, we can measure the duration of a day in hours, minutes or seconds and get a different numerical value corresponding to each unit (24h, 1440 min, 86400s) but a day is still a day no matter what units we use to measure it.
If we take the equality we wrote (above) between values in meters and centimeters, we can convert it to a conversion factor and use it.
![]()
e.g., ![]() . The Dimension is unchanged. The distance is same in both 130 cm and 1.3 m so the conversion factor did not change the size of the thing we measured; only the units in which we expressed that distance.
. The Dimension is unchanged. The distance is same in both 130 cm and 1.3 m so the conversion factor did not change the size of the thing we measured; only the units in which we expressed that distance.
Note that the conversion factor has units of cm m–1 but is in effect dimensionless since both cm and m are units of the dimension [L] length.
Example
The speed of a car is 50.0 mph. What is its speed equal to in meters per second?
In this example, we probably need to look up one equality between kilometers and miles before we can create all the appropriate conversion factors. The others are probably created from commonly known equalities. Thus, we look up 1km = 0.6214 miles. The rest, we know: 1000m = 1 km, 1 h = 60 min, 1 min = 60 s. Note that the first conversion (km to miles) is not a defined number and thus, the number of significant figures is limited by the accuracy of our measurements. In this case, we know the conversion to 4 sig figs. The other three conversion factors are all defined quantities and as such, have an infinite number of sig figs. Thus, when we do the math, we should get a final answer that has 3 sig figs since that is the smallest number in any of the values used in this problem and it involves only multiplication and division.
![]()
This kind of use of conversion factors can also be written more quickly in extended fraction form as follows:
![]()
At first glance, this extended fraction form may be a bit more complicated looking but it is actually simpler if you simply think of it as multiplications (horizontal) and divisions (vertical). Thus, simply multiply all the numbers across each row of the table and then divide the top by the bottom. Clearly this way, we can also easily check to see that the units cancel out properly. In the end, I expressed the final answer in a single line where the unit m s–1 represents the m/s.
Also notice that in each conversion factor, the denominator equals the numerator (e.g., one minute equals sixty seconds). Thus, the conversion factors all have unity (a.k.a. “one”) magnitude. So each conversion factor was simply multiplying by “one”. In other words, the speed of the car is not different. It’s just expressed in a different set of units.
Example
A certain synthetic process yields 7.83×10–2 g of product per second. After 5.00 days of continuous reacting, how many kilograms will be produced?
In this example, we are looking to combine two different dimensional values to get a third value. The first number (7.83×10–2 g/s) is a rate (Dimensions = amount/time) and the second (5.00 days) has dimensions of time. So if we multiply the two together, we will cancel out the dimension time to get amount, as needed. Also, we need to convert the units in such a way as to properly cancel out the units. Thus, we need conversion factors from seconds to days and from g to kg.
![]()
As we did in the first example, we can do this more quickly in extended fraction form:
![]()
Here, the amount 5 days is not a conversion factor. It’s merely the amount of time we ran the reaction and is a simple number. We place it in the top of our extended fraction to keep the math correct. In this case, all the conversion factors are defined values and have infinite sig figs. The rate or production and the time of the reaction are measured values given in the problem. These have three sig figs each so the answer has three sig figs.
Here, we used a set of conversion factors derived from commonly known equalities like 60 seconds in a minute (60s = 1min), 60 minutes in an hour (60 min = 1h) and 24 hours in a day (24h = 1day).
I will be using extended fractional form for many worked problems in this course. You would do well to get used to it. In fact, the extended fractional form is preferred for usage in some professions because it makes error checking very easy. For example, nurses are trained to use this method for calculating dosages for meds so their supervisors can easily double check their calculations and thereby reduce medication errors that might harm patients.
Keeping track of units and doing the conversions may seem minor but it can be the most important calculation you do. For example, in the 1980’s, a 767 passenger jet with many passengers on board, ran out of fuel over Manitoba. The pilot had to make an emergency “dead–stick” landing and could only reach an old airport runway at an airport (Gimli MB) that had long been abandoned and converted into a drag strip. News reports of the day put the error as a unit conversion problem. Perhaps someone took a shortcut in their calculations and except for the heroic efforts of the pilot and copilot, it could have spelled disaster. See the movie “The Gimli Glider” for interest.
For a CBC archives video clip, click here. For a later more detailed writeup on the Gimli Glider, click here.
1.4.2: Conversion Factors and Significant Figures
When using conversion factors, we need to be aware that there are different kinds of these factors. Some are defined quantities, such as 1 foot = 12 inches, or 1 kg = 1000g. These conversion factors are defined values (whole–number ratios) and have an infinite number of sig figs. Other conversion factors are measured conversions and therefore have a limited number of sig figs. Conversions between SI and Imperial systems are often just measured conversions. originally, one inch used to be approximately 2.54 cm. We were told that this conversion factor had just 3 sig figs. It was very close but not exactly that value. As of May 2019 one inch is “DEFINED” to be 2.54 cm. It’s now a defined value and thus there are infinite sig figs in the conversion factor (1 in = 2.54 cm exactly). In other words, we actually changed the length of an inch so that it is now defined, based on the SI unit of length, cm.
In summary:
- defined conversion factors have infinite number of sig. figs.
- measured conversion factors have a limited number of sig. figs.
1.4.3: SI Units
The International System of units (SI for the French name: Système International) is generally used for scientific measurements. We are familiar with some of them, such as kilograms, kilometers, etc. There are generally two classes of SI units, SI Base units and SI derived units.
SI Base Units
These units are the basis upon which the entire SI system is built. Their definitions are often build on some measurable physical property. These definitions have changed over time in some cases. Take for example, the metre. Originally, it was defined as one ten–millionth of the distance from the north pole to the equator along the meridian that passes through Paris. Later, it was defined as length of 9 192 631 770 wavelengths of the microwave radiation of a certain transition of 133Cs. Now, it’s defined to be the distance traveled by light in a vacuum in 1/299 792 458 of a second. (see here)
| Base Quantity | SI Base Unit | |
| Name | Symbol | |
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| electric current | ampere | A |
| thermodynamic temperature | kelvin | K |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
SI Derived Units
There are many other SI units that are used regularly which are derived from combinations of these base units. Of the extremely large possible number of such combinations, there are 22 which are named. The table below shows a few of these used in this course.
| SI Derived Unit | ||||
| Derived Quantity | Name | Symbol | Expression in terms of other SI units | Expression in terms of SI base units |
| frequency | hertz | Hz | – | s–1 |
| force | newton | N | – | m×kg×s–2 |
| pressure | pascal | Pa | N/m2 | m–1×kg×s–2 |
| energy, work, quantity of heat | joule | J | N×m | m2×kg×s–2 |
| power | watt | W | J/s | m2×kg×s–3 |
| electric charge | coulomb | C | – | s×A |
| electric potential difference | volt | V | W/A | m2×kg×s–3×A–1 |
Because of the huge range of values, we often simplify the representation of a measured amount by using a prefix to represent a power of 10. For example, we may measure the length of a soccer field in meters (m), the length of a our finger in centimeters (cm) and the length of a city street street in kilometers (km). Each is a measure of length based on metres but each has a different order of magnitude, defined by the prefix or lack thereof. Here is a fairly complete list of accepted SI prefixes.
|
|
You should make a point to memorize the prefixes between 1012 and 10–12 as you will be encountering them repeatedly in this course.
These tables are taken from this website.
1.5: Logarithms and Exponentials
Logarithms are commonly used to compress the scale of numbers to an easily manageable range. For example, we are familiar with the Richter scale for earthquakes where every unit represents an order of magnitude in earthquake intensity. Thus, a quake measuring 5 on the Richter scale is 10 times stronger than one measuring 4 on that scale. Using simple numbers, we can express the energy of earthquakes that can span many orders of magnitude.
To manipulate logarithms and exponential numbers, there are a few simple rules.
When multiplying exponential numbers, add the exponents if same base:
104 × 106 = 10(4+6) = 1010
When dividing exponential numbers, subtract the exponents if same base:
104 ÷ 106 = 10(4–6) = 10–2
Logarithms are like exponentials:
When you multiply two logarithmic numbers, add their logs if same base.
When you divide two logarithmic numbers, subtracts their logs if same base.
What is a logarithm? It depends on the Base used.
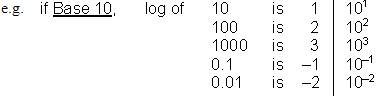
If the number we are working with is not an even power of the base, we separate the number into a coefficient (a.k.a. mantissa) and an exponent (order of magnitude) and add their logarithms. This way, we isolate the sig. fig. information in the coefficient so we can keep track.
| 37800 = 3.78 × 104 : log(3.78 × 104) | = log 3.78 + log 104 |
| = 0.5775 + 4 = 0.578 + 4 (sig. fig.!) | |
| = 4.578 (we gained a ‘sig fig’) |
| 0.000378 = 3.78 × 10–4 : log(3.78 × 10–4) | = log 3.78 + log 10–4 |
| = 0.5775 + (–4) | |
| = –3.4225 | |
| = –3.423 (we gained a ‘sig fig’) |
To go from a log to a real number, we find the antilog of that number. the function is defined as antilog a = 10a. We separate a into the exponent and positive coefficient separately so we can keep track of sig figs.
| antilog(6.574) = | antilog(6 + .574) = | antilog(.574) × antilog(6) = | 3.75 × 106 |
| antilog(0.574) = | antilog(0 + .574) = | antilog(.574) × antilog(0) = | 3.75 × 100 |
| antilog(–0.426) = | antilog(–1 + .574) = | antilog(.574) × antilog(–1) = | 3.75 × 10–1 |
| antilog(–2.426) = | antilog(–3 + .574) = | antilog(.574) × antilog(–3) = | 3.75 × 10–3 |
Here are a few rules for using logarithms in mathematics.
| define: log x = | a | ||
| so: antilog (log x) = | antilog a | ||
| functions cancel so: x = | antilog a | ||
| x = | 10a | ||
| define log x = a | and log y = b | ||
| x × y = | 10a × 10b | = 10(a+b) | |
| log (x × y) = | log(10a × 10b ) | = a + b | in other words… log (x × y) = log x + log y |
| x/y = | 10a/10b | = 10(a–b) | |
| log (x/y) = | log (10a/10b) | = a – b | in other words… log (x/y) = log x – log y |
| xn = | (10a)n | = 10(n×a) | in other words… log xn = n log x |
Natural logs are still logs but to base e: e = 2.718281828… (Careful, this ‘e’ is not the same as the electronic charge ‘e’)
Log to base e (loge) is often abbreviated as ln. Thus, if loge x = a then x = ea. using the same logic as for base 10:
ln e = 1, ln e2 = 2, etc…
To convert between log and ln:
Let’s say that we need to calculate the natural log of a number as in ln y = x but our calculator can only calculate base 10 logarithms (log y). In that case, we can convert from log y to ln y quite easily knowing the equality
ln y = 2.303 × log y
thus, we can write:
x = 2.303 × log y
1.6: Practice Problems
1.1 Calculate the following mathematical expressions and give the answer to the correct number of sig figs. (Answers to practice problems are below)
| a. |
b. |
c. |
d. |
e. |
| f. |
g. |
h . |
i. |
j. |
| k. |
l. |
m. |
1.2 An American vehicle’s speedometer is calibrated in units of miles per hour (mph). The vehicle is travelling in Canada, where the speed limits are posted in metric units (km/h). What speed must the driver of the American vehicle maintain in order to remain in compliance with a posted speed limit of 65 km/h?
(Use the equalities: 1 in = 2.54 cm, 12 in = 1 ft, 1 mile = 5280 ft)
1.3 An industrial plant produces 1.4 kg/s of product. How much product will the plant produce in one week (7 days) if the plant operates 24hours–a–day with no stoppages or slowdowns?
1.4 Two solutions are sampled and their pH is found to be 4.3 and 5.8, respectively. Find an expression to determine the ratio of the [![]() ] concentrations for the two solutions and then calculate the ratio.
] concentrations for the two solutions and then calculate the ratio.
Answers to practice problems
1.1
a. ![]()
b. ![]() or
or ![]()
c. ![]()
d. ![]()
e. ![]() more correctly
more correctly ![]()
f. ![]() Go with the smallest sig figs.
Go with the smallest sig figs.
g. ![]() or
or ![]()
h. ![]() or
or ![]()
i. ![]() more correctly
more correctly ![]()
j. ![]() the 2 is the power of 10, not a sig fig.
the 2 is the power of 10, not a sig fig.
k. ![]() See how you have to work your sig figs step by step.
See how you have to work your sig figs step by step.
l. ![]() more correctly
more correctly ![]()
m. ![]() Note that the 1 in the 1.1549 is the power of 10. You’ve ‘gained’ a sig fig.
Note that the 1 in the 1.1549 is the power of 10. You’ve ‘gained’ a sig fig.
1.2 ![]() or
or ![]() .
.
1.3 Using the extended fraction formalism:
![]()
1.4 We know that we can use the concentration of the hydronium ion to determine ![]() . Or, in exponential form,
. Or, in exponential form, ![]() . So to get an expression for the ratio of the concentrations of the two solutions, we take divide two equations (one for each solution).
. So to get an expression for the ratio of the concentrations of the two solutions, we take divide two equations (one for each solution).
![]()
So, we can calculate the concentration ratio:
![]()
So although the pH values are only separated by a difference of 1.5, solution 1 is 32 times more concentrated than solution 2.

