Chapter 1.5: Use a General Strategy to Solve Linear Equations
Learning Objectives
By the end of this section, you will be able to:
- Solve equations using a general strategy
- Classify equations
Solve Equations Using the General Strategy
Until now we have dealt with solving one specific form of a linear equation. It is time now to lay out one overall strategy that can be used to solve any linear equation. Some equations we solve will not require all these steps to solve, but many will.
Beginning by simplifying each side of the equation makes the remaining steps easier.
EXAMPLE 1. How to Solve Linear Equations Using the General Strategy





TRY IT 1.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 1.2
Solve: ![]() .
.
Show answer
![]()
General strategy for solving linear equations.
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.
EXAMPLE 2
Solve: ![]() .
.
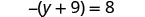 |
||
| Simplify each side of the equation as much as possible by distributing. | 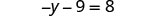 |
|
| The only |
||
| Add |
 |
|
| Simplify. | 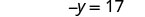 |
|
| Rewrite |
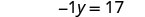 |
|
| Make the coefficient of the variable term to equal to |
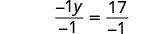 |
|
| Simplify. |  |
|
| Check: Let |
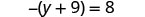 |
|
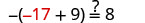 |
||
 |
||
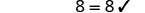 |
||
TRY IT 2.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 2.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 3
Solve: ![]() .
.
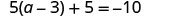 |
|
| Simplify each side of the equation as much as possible. | |
| Distribute. | 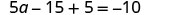 |
| Combine like terms. | 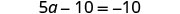 |
| The only |
|
| Add |
 |
| Simplify. | 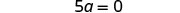 |
| Make the coefficient of the variable term to equal to |
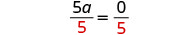 |
| Simplify. |  |
| Check: | 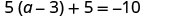 |
| Let |
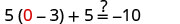 |
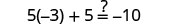 |
|
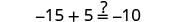 |
|
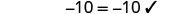 |
TRY IT 3.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 3.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 4
Solve: ![]() .
.
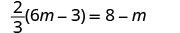 |
|
| Distribute. | 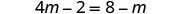 |
| Add |
 |
| Simplify. | 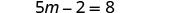 |
| Add |
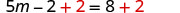 |
| Simplify. | 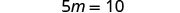 |
| Divide by |
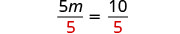 |
| Simplify. | 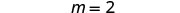 |
| Check: |  |
| Let |
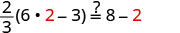 |
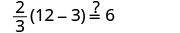 |
|
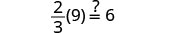 |
|
 |
TRY IT 4.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 4.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 5
Solve: ![]() .
.
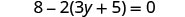 |
|
| Simplify—use the Distributive Property. | 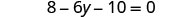 |
| Combine like terms. |  |
| Add |
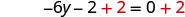 |
| Simplify. | 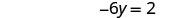 |
| Divide both sides by |
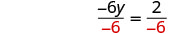 |
| Simplify. |  |
| Check: Let |
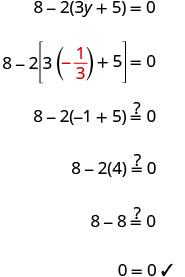 |
TRY IT 5.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 5.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 6
Solve: ![]() .
.
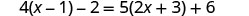 |
|
| Distribute. | 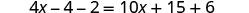 |
| Combine like terms. | 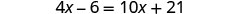 |
| Subtract |
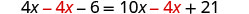 |
| Simplify. | 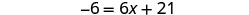 |
| Subtract |
 |
| Simplify. | 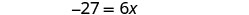 |
| Divide by 6. |  |
| Simplify. |  |
| Check: | 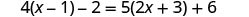 |
| Let |
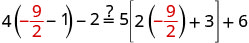 |
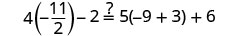 |
|
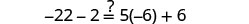 |
|
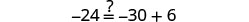 |
|
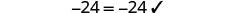 |
TRY IT 6.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 6.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 7
Solve: ![]() .
.
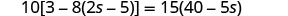 |
|
| Simplify from the innermost parentheses first. | 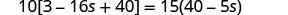 |
| Combine like terms in the brackets. | 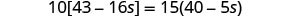 |
| Distribute. | 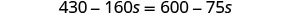 |
| Add |
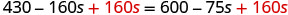 |
| Simplify. | 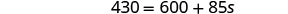 |
| Subtract 600 to get the constants to the left. | 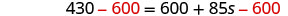 |
| Simplify. | 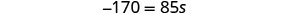 |
| Divide. |  |
| Simplify. | 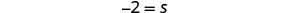 |
| Check: | 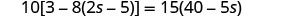 |
| Substitute |
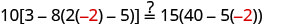 |
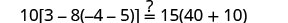 |
|
 |
|
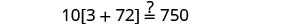 |
|
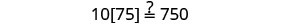 |
|
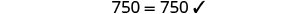 |
TRY IT 7.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 7.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 8
Solve: ![]() .
.
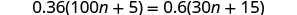 |
|
| Distribute. |  |
| Subtract |
 |
| Simplify. | 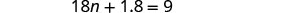 |
| Subtract |
 |
| Simplify. | 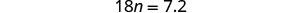 |
| Divide. | 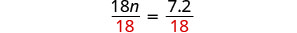 |
| Simplify. |  |
| Check: | 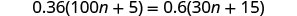 |
| Let |
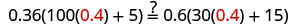 |
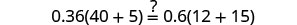 |
|
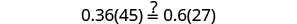 |
|
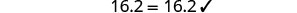 |
TRY IT 8.1
Solve: ![]() .
.
Show answer
![]()
TRY IT 8.2
Solve: ![]() .
.
Show answer
![]()
Classify Equations
Consider the equation we solved at the start of the last section, ![]() . The solution we found was
. The solution we found was ![]() . This means the equation
. This means the equation ![]() is true when we replace the variable, x, with the value
is true when we replace the variable, x, with the value ![]() . We showed this when we checked the solution
. We showed this when we checked the solution ![]() and evaluated
and evaluated ![]() for
for ![]() .
.
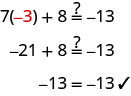
If we evaluate ![]() for a different value of x, the left side will not be
for a different value of x, the left side will not be ![]() .
.
The equation ![]() is true when we replace the variable, x, with the value
is true when we replace the variable, x, with the value ![]() , but not true when we replace x with any other value. Whether or not the equation
, but not true when we replace x with any other value. Whether or not the equation ![]() is true depends on the value of the variable. Equations like this are called conditional equations.
is true depends on the value of the variable. Equations like this are called conditional equations.
All the equations we have solved so far are conditional equations.
Conditional equation
An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation.
Now let’s consider the equation ![]() . Do you recognize that the left side and the right side are equivalent? Let’s see what happens when we solve for y.
. Do you recognize that the left side and the right side are equivalent? Let’s see what happens when we solve for y.
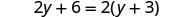 |
|
| Distribute. | 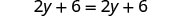 |
| Subtract |
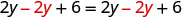 |
| Simplify—the |
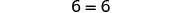 |
But ![]() is true.
is true.
This means that the equation ![]() is true for any value of y. We say the solution to the equation is all of the real numbers. An equation that is true for any value of the variable like this is called an identity.
is true for any value of y. We say the solution to the equation is all of the real numbers. An equation that is true for any value of the variable like this is called an identity.
Identity
An equation that is true for any value of the variable is called an identity.
The solution of an identity is every real number.
What happens when we solve the equation ![]() ?
?
 |
|
| Subtract |
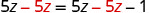 |
| Simplify—the |
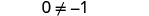 |
But ![]() .
.
Solving the equation ![]() led to the false statement
led to the false statement ![]() . The equation
. The equation ![]() will not be true for any value of z. It has no solution. An equation that has no solution, or that is false for all values of the variable, is called a contradiction.
will not be true for any value of z. It has no solution. An equation that has no solution, or that is false for all values of the variable, is called a contradiction.
Contradiction
An equation that is false for all values of the variable is called a contradiction.
A contradiction has no solution.
EXAMPLE 9
Classify the equation as a conditional equation, an identity, or a contradiction. Then state the solution.
![]()
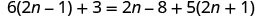 |
|
| Distribute. | 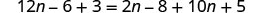 |
| Combine like terms. | 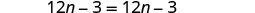 |
| Subtract |
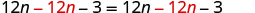 |
| Simplify. |  |
| This is a true statement. | The equation is an identity. The solution is every real number. |
TRY IT 9.1
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
![]()
Show answer
identity; all real numbers
TRY IT 9.2
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
![]()
Show answer
identity; all real numbers
EXAMPLE 10
Classify as a conditional equation, an identity, or a contradiction. Then state the solution.
![]()
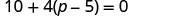 |
|
| Distribute. | 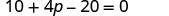 |
| Combine like terms. | 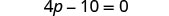 |
| Add |
 |
| Simplify. | 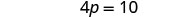 |
| Divide. | 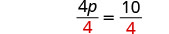 |
| Simplify. | 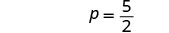 |
| The equation is true when |
This is a conditional equation. The solution is |
TRY IT 10.1
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: ![]()
Show answer
conditional equation; ![]()
TRY IT 10.2
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: ![]()
Show answer
conditional equation; ![]()
EXAMPLE 11
Classify the equation as a conditional equation, an identity, or a contradiction. Then state the solution.
![]()
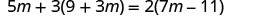 |
|
| Distribute. | 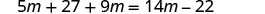 |
| Combine like terms. | 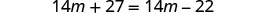 |
| Subtract |
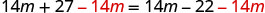 |
| Simplify. | 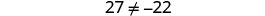 |
| But |
The equation is a contradiction. It has no solution. |
TRY IT 11.1
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
![]()
Show answer
contradiction; no solution
TRY IT 11.2
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
![]()
Show answer
contradiction; no solution
Type of equation – Solution
| Type of equation | What happens when you solve it? | Solution |
|---|---|---|
| Conditional Equation | True for one or more values of the variables and false for all other values | One or more values |
| Identity | True for any value of the variable | All real numbers |
| Contradiction | False for all values of the variable | No solution |
Key Concepts
- General Strategy for Solving Linear Equations
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution.
Substitute the solution into the original equation.
- Simplify each side of the equation as much as possible.
Glossary
- conditional equation
- An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation.
- contradiction
- An equation that is false for all values of the variable is called a contradiction. A contradiction has no solution.
- identity
- An equation that is true for any value of the variable is called an identity. The solution of an identity is all real numbers.
Practice Makes Perfect
Solve Equations Using the General Strategy for Solving Linear Equations
In the following exercises, solve each linear equation.
| 1. |
2. |
| 3. |
4. |
| 5. |
6. |
| 7. |
8. |
| 9. |
10. |
| 11. |
12. |
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. |
26. |
| 27. |
28. |
| 29. |
30. |
| 31. |
32. |
| 33. |
34. |
| 35. |
36. |
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. |
48. |
| 49. |
50. |
| 51. |
52. |
| 53. |
54. |
| 55. |
56. |
| 57. |
58. |
Classify Equations
In the following exercises, classify each equation as a conditional equation, an identity, or a contradiction and then state the solution.
| 59. |
60. |
| 61. |
62. |
| 63. |
64. |
| 65. |
66. |
| 67. |
68. |
| 69. |
70. |
| 71. |
72. |
| 73. |
74. |
| 75. |
76. |
| 77. |
78. |
Everyday Math
| 79. Coins. Rhonda has $1.90 in nickels and dimes. The number of dimes is one less than twice the number of nickels. Find the number of nickels, n, by solving the equation |
80. Fencing. Micah has 44 feet of fencing to make a dog run in his yard. He wants the length to be 2.5 feet more than the width. Find the length, L, by solving the equation |
Writing Exercises
| 81. Explain why you should simplify both sides of an equation as much as possible before collecting the variable terms to one side and the constant terms to the other side. | 82. Using your own words, list the steps in the general strategy for solving linear equations. |
| 83. Solve the equation |
84. What is the first step you take when solving the equation |
Answers
| 1. |
3. |
5. |
| 7. |
9. |
11. |
| 13. |
15. |
17. |
| 19. |
21. |
23. |
| 25. |
27. |
29. |
| 31. |
33. |
35. |
| 37. |
39. |
41. |
| 43. |
45. |
47. |
| 49. |
51. |
53. |
| 55. |
57. |
59. identity; all real numbers |
| 61. identity; all real numbers | 63. conditional equation; |
65. conditional equation; |
| 67. contradiction; no solution | 69. contradiction; no solution | 71. conditional equation; |
| 73. contradiction; no solution | 75. identity; all real numbers | 77. identity; all real numbers |
| 79. 8 nickels | 81. Answers will vary. | 83. Answers will vary. |
Attributions
This chapter has been adapted from “Use a General Strategy to Solve Linear Equations” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

