Chapter 5.10: Completing the Square
How To “Complete the Square” Visually[1]
Let’s use an area model to visualize how to complete the square of the following equation:
![]()
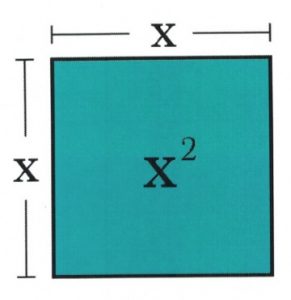
The area model used by Brett Berry is fairly straightforward, having multiple variations and forms that can be found online. The standard explanation begins by representing ![]() as a square whose sides are both
as a square whose sides are both ![]() units in length and make an area of
units in length and make an area of ![]() .
.
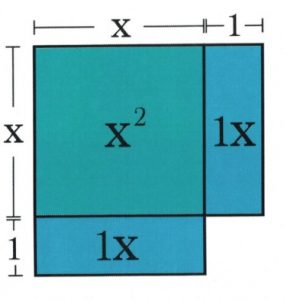
Next, add ![]() to the block defined as
to the block defined as ![]() . This is done by taking the
. This is done by taking the ![]() block and cutting it in half, then add to both sides of your original square
block and cutting it in half, then add to both sides of your original square ![]() . This acts to continue the sides of
. This acts to continue the sides of ![]() in two directions by
in two directions by ![]() .
.
 In this example, the square length on each side has increased by 1, but as you can see from the diagram, this larger square is missing the corner piece. To complete the square, add a small piece to complete the visual square. The question is, what is the area of this missing piece?
In this example, the square length on each side has increased by 1, but as you can see from the diagram, this larger square is missing the corner piece. To complete the square, add a small piece to complete the visual square. The question is, what is the area of this missing piece?
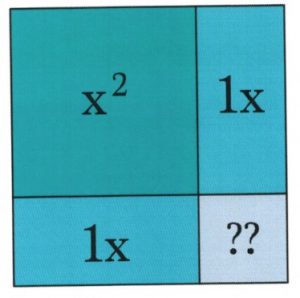 Since the blue blocks adjacent to our missing piece are both 1 unit wide, deduce that the missing block has an area of 1 × 1 = 1.
Since the blue blocks adjacent to our missing piece are both 1 unit wide, deduce that the missing block has an area of 1 × 1 = 1.
Also note that, by adding together the outermost units of the square, the area of the square becomes the desired binomial squared ![]() .
.
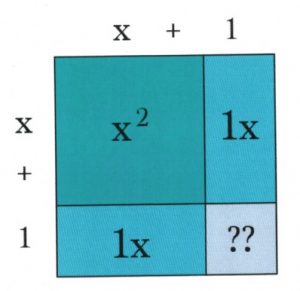 Now, all that’s left to do is literally complete the square and adjust for the extra units. To do this, first, fill in the area of the purple square, which is known to be 1. Since the original equation had a constant of 12, subtract 1 from 12 to account for the 1 added to the square.
Now, all that’s left to do is literally complete the square and adjust for the extra units. To do this, first, fill in the area of the purple square, which is known to be 1. Since the original equation had a constant of 12, subtract 1 from 12 to account for the 1 added to the square.
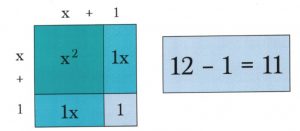
The square is now complete! The square is ![]() with 11 leftover. The extra 11 can simply be added to the end of our binomial squared:
with 11 leftover. The extra 11 can simply be added to the end of our binomial squared: ![]() .
.
In the problems most likely be required to solve, ![]() , so the original equation will not be written as
, so the original equation will not be written as ![]() ; rather, it will be
; rather, it will be ![]() .
.
Example 1
Solve for ![]() in the equation
in the equation ![]() .
.
The first step is to complete the square. Rather than drawing out a sketch to show the process of completing the square, simply take half the middle term and rewrite ![]() as
as ![]() .
.
When squared out ![]() , it is
, it is ![]() .
.
Note that this is 4 larger than the original ![]() . This means that
. This means that ![]() is the same as
is the same as ![]() .
.
The equation needed to be solved has now become ![]() . First, add 4 to each side:
. First, add 4 to each side:
![Rendered by QuickLaTeX.com \[\begin{array}{rrrrrrr} 0&=&(x&+&4)^2&-&4 \\ +4&=&&&&+&4 \\ \midrule 4&=&(x&+&4)^2&& \\ \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-71d560de7b68c7076893878f57613177_l3.png)
Now take the square root from both sides:
![]()
Subtracting 4 from both sides leaves ![]() , which gives the solutions
, which gives the solutions ![]() and
and ![]() .
.
It is always wise to check answers in the original equation, which for these two yield:
![Rendered by QuickLaTeX.com \[\begin{array}{rrcllrl} x&=&-6:&&&& \\ \\ 0&=&x^2&+&8x&+&12 \\ 0&=&(-6)^2&+&8(-6)&+&12 \\ 0&=&36&-&48&+&12\checkmark \\ \\ \\ x&=&-2:&&&& \\ \\ 0&=&x^2&+&8x&+&12 \\ 0&=&(-2)^2&+&8(-2)&+&12 \\ 0&=&4&-&16&+&12\checkmark \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-89f9aae33eae3f7eb84747f0c835ea41_l3.png)
Sometimes, it is required to complete the square where there is some value ≠ 1 in front of the ![]() . For example:
. For example:
Example 2
Solve for ![]() in the equation
in the equation ![]() .
.
The first step is to factor 2 from both terms in ![]() , which then leaves
, which then leaves ![]() .
.
Isolating ![]() yields
yields ![]() .
.
As before, complete the square for ![]() , which yields
, which yields ![]() . When squared out
. When squared out ![]() , you get
, you get ![]() .
.
Now add 9 to the other side of the equation:
![]()
Simplifying this yields:
![]()
Now take the square root from both sides:
![]()
Which leaves:
![]()
Subtract 3 from both sides:
![]()
Rationalizing the denominator yields:
![]()
When checking these answers in the original equation, both solutions are valid.
Questions
Find the value that completes the square and then rewrite as a perfect square.
Solve each equation by completing the square.
Answers to odd questions
1. 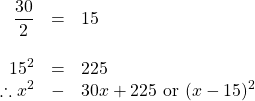
3. 
5. 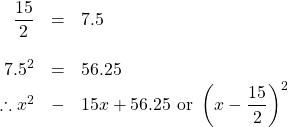
7. 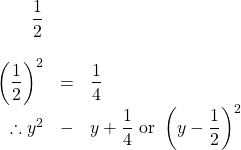
9. 
![]()
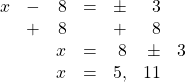
11. 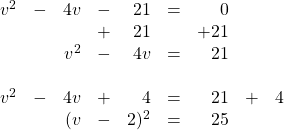
![]()
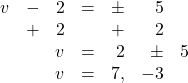
13. ![]()
![]()
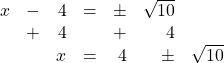
15. 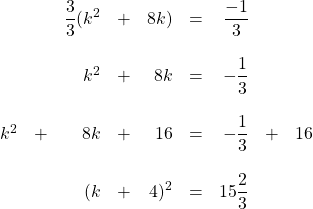
![]()
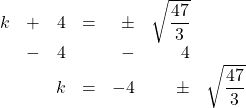
- Adapted from Brett Berry ↵

