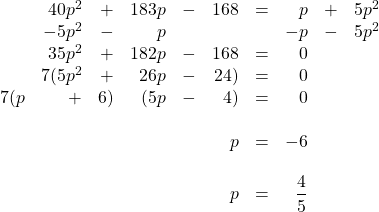Chapter 5.8: Solving Quadriatic Equations by Factoring
Solving quadratics is an important algebraic tool that finds value in many disciplines. Typically, the quadratic is in the form of ![]() , which when graphed is a parabola. Of special importance are the
, which when graphed is a parabola. Of special importance are the ![]() -values that are found when
-values that are found when ![]() , which show up when graphed as the parabola crossing the
, which show up when graphed as the parabola crossing the ![]() -axis. For a trinomial, there can be as many as three
-axis. For a trinomial, there can be as many as three ![]() -axis crossings. The following show the possible number of
-axis crossings. The following show the possible number of ![]() -axis intercepts for 2nd degree (quadratic) to 7th degree (septic) functions. Please note that if the fifth degree polynomial were shifted down a few values, it would also show 5
-axis intercepts for 2nd degree (quadratic) to 7th degree (septic) functions. Please note that if the fifth degree polynomial were shifted down a few values, it would also show 5 ![]() -axis intercepts. It is these
-axis intercepts. It is these ![]() -axis intercepts that are of interest.
-axis intercepts that are of interest.
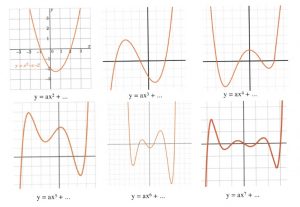
The approach to finding these ![]() -intercepts is elementary: set
-intercepts is elementary: set ![]() in the original equation and factor it. Once the equation is factored, then find the
in the original equation and factor it. Once the equation is factored, then find the ![]() -values that solve for 0. This is shown in the next few examples.
-values that solve for 0. This is shown in the next few examples.
Example 1
Solve the following quadratic equation: ![]() .
.
In this problem there are two separate binomials: ![]() and
and ![]() . Since their product is equal to 0, there will be two solutions: the value for
. Since their product is equal to 0, there will be two solutions: the value for ![]() that makes
that makes ![]() and the value for
and the value for ![]() that makes
that makes ![]() .
.
These are:
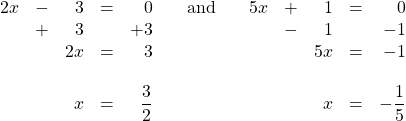
Example 2
Solve the following polynomial equation: ![]() .
.
For this polynomial, there are four different solutions:
![]()
Solving for these four x-values gives us:
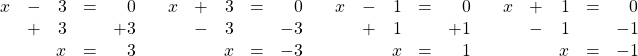
The solutions are: ![]() .
.
It would be nice if there were only given factored equations to solve, but that is not how it goes. You are generally required to factor the equation first before it can be solved.
Example 3
Solve the following quadratic equation: ![]() .
.
First, factor ![]() and get
and get ![]() .
.
Now, solve for ![]() and
and ![]() .
.
Solving these two binomials yields:
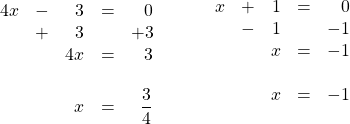
Questions
Solve each of the following polynomials by using factoring.
Answers to odd questions
1. 
3. 
5. 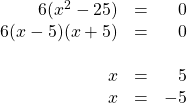
7. 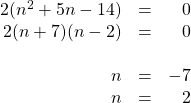
9. 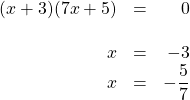
11. 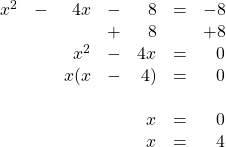
13. 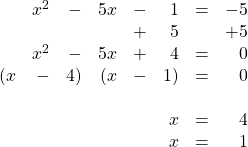
15. 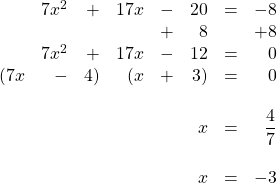
17. 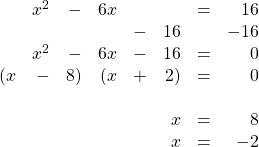
19. 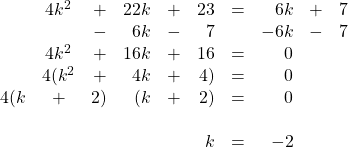
21. 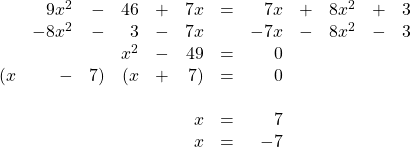
23.