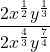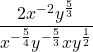Chapter 8.6: Radicals and Rational Exponents
When simplifying radicals that use fractional exponents, the numerator on the exponent is divided by the denominator. All radicals can be shown as having an equivalent fractional exponent. For example:
![]()
Radicals having some exponent value inside the radical can also be written as a fractional exponent. For example:
![]()
The general form that radicals having exponents take is:
![]()
Should the reciprocal of a radical having an exponent, it would look as follows:
![]()
In both cases shown above, the power of the radical is ![]() and the root of the radical is
and the root of the radical is ![]() . These are the two forms that a radical having an exponent is commonly written in. It is convenient to work with a radical containing an exponent in one of these two forms.
. These are the two forms that a radical having an exponent is commonly written in. It is convenient to work with a radical containing an exponent in one of these two forms.
Example 1
Evaluate ![]() .
.
Converting to a radical form:
![]()
First, the cube root of 27 will reduce to 3, which leaves:
![]()
Once the radical having an exponent is converted into a pure fractional exponent, then the following rules can be used.
Properties of Exponents
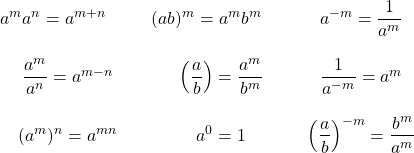
Example 2
Simplify ![]() .
.
First, you need to separate the different variables:
![]() becomes
becomes ![]()
Combining the exponents yields:
![]()
Which results in:
![]()
Which simplifies to:
![]()
Example 3
Simplify ![]() .
.
First, separate the different variables:
![]() becomes
becomes ![]() [1]
[1]
Combining the exponents yields:
![]()
Which gives:
![]()
Which simplifies to:
![]()
Questions
Write each of the following fractional exponents in radical form.
Write each of the following radicals in exponential form.
Evaluate the following.
Simplify. Your answer should only contain positive exponents.
Answers to odd questions
1. ![]()
3. ![]()
5. ![]()
7. ![]()
9. ![]() or
or ![]()
11. ![]()
13. ![]()
15. ![]()
17. ![]()
19. ![]()
21. ![]()
23. ![]()
25. ![]()
- When we divide by an exponent, we subtract powers. ↵