Chapter 1.1: Exponents and Scientific Notation
Learning Objectives
In this section students will:
- Use the product rule of exponents.
- Use the quotient rule of exponents.
- Use the power rule of exponents.
- Use the zero exponent rule of exponents.
- Use the negative rule of exponents.
- Find the power of a product and a quotient.
- Simplify exponential expressions.
- Use scientific notation.
Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is 2,048 pixels by 1,536 pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to 48 bits per frame, and can shoot the equivalent of 24 frames per second. The maximum possible number of bits of information used to film a one-hour (3,600-second) digital film is then an extremely large number.
Using a calculator, we enter ![]() and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately
and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately ![]() bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
Using the Product Rule of Exponents
Consider the product ![]() Both terms have the same base, x, but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
Both terms have the same base, x, but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
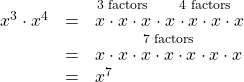
The result is that ![]()
Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
Now consider an example with real numbers.
We can always check that this is true by simplifying each exponential expression. We find that ![]() is 8,
is 8, ![]() is 16, and
is 16, and ![]() is 128. The product
is 128. The product ![]() equals 128, so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
equals 128, so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
The Product Rule of Exponents
For any real number ![]() and natural numbers
and natural numbers ![]() and
and ![]() the product rule of exponents states that
the product rule of exponents states that
Using the Product Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the product rule to simplify each expression.
At first, it may appear that we cannot simplify a product of three factors. However, using the associative property of multiplication, begin by simplifying the first two.
Notice we get the same result by adding the three exponents in one step.
Try It
Write each of the following products with a single base. Do not simplify further.
Show Solution
Using the Quotient Rule of Exponents
The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. In a similar way to the product rule, we can simplify an expression such as ![]() where
where ![]() Consider the example
Consider the example ![]() Perform the division by canceling common factors.
Perform the division by canceling common factors.
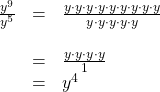
Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.
In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
For the time being, we must be aware of the condition ![]() Otherwise, the difference
Otherwise, the difference ![]() could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.
could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.
The Quotient Rule of Exponents
For any real number ![]() and natural numbers
and natural numbers ![]() and
and ![]() such that
such that ![]() the quotient rule of exponents states that
the quotient rule of exponents states that
Using the Quotient Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the quotient rule to simplify each expression.
Try It
Write each of the following products with a single base. Do not simplify further.
Show Solution
Using the Power Rule of Exponents
Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents. Consider the expression ![]() The expression inside the parentheses is multiplied twice because it has an exponent of 2. Then the result is multiplied three times because the entire expression has an exponent of 3.
The expression inside the parentheses is multiplied twice because it has an exponent of 2. Then the result is multiplied three times because the entire expression has an exponent of 3.

The exponent of the answer is the product of the exponents: ![]() In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
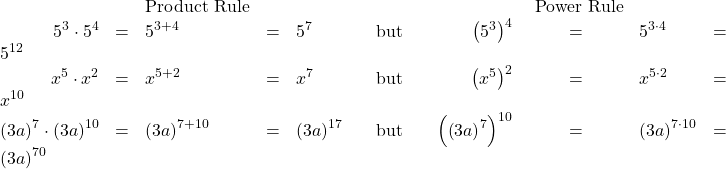
The Power Rule of Exponents
For any real number ![]() and positive integers
and positive integers ![]() and
and ![]() the power rule of exponents states that
the power rule of exponents states that
Using the Power Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the power rule to simplify each expression.
Try It
Write each of the following products with a single base. Do not simplify further.
Show Solution
Using the Zero Exponent Rule of Exponents
Return to the quotient rule. We made the condition that ![]() so that the difference
so that the difference ![]() would never be zero or negative. What would happen if
would never be zero or negative. What would happen if ![]() In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
If we were to simplify the original expression using the quotient rule, we would have
If we equate the two answers, the result is ![]() This is true for any nonzero real number, or any variable representing a real number.
This is true for any nonzero real number, or any variable representing a real number.
The sole exception is the expression ![]() This appears later in more advanced courses, but for now, we will consider the value to be undefined.
This appears later in more advanced courses, but for now, we will consider the value to be undefined.
The Zero Exponent Rule of Exponents
For any nonzero real number ![]() the zero exponent rule of exponents states that
the zero exponent rule of exponents states that
Using the Zero Exponent Rule
Simplify each expression using the zero exponent rule of exponents.
Show Solution
Use the zero exponent and other rules to simplify each expression.
Try It
Simplify each expression using the zero exponent rule of exponents.
Show Solution
Using the Negative Rule of Exponents
Another useful result occurs if we relax the condition that ![]() in the quotient rule even further. For example, can we simplify
in the quotient rule even further. For example, can we simplify ![]() When
When ![]() —that is, where the difference
—that is, where the difference ![]() is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
Divide one exponential expression by another with a larger exponent. Use our example, ![]()
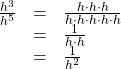
If we were to simplify the original expression using the quotient rule, we would have
Putting the answers together, we have ![]() This is true for any nonzero real number, or any variable representing a nonzero real number.
This is true for any nonzero real number, or any variable representing a nonzero real number.
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.
We have shown that the exponential expression ![]() is defined when
is defined when ![]() is a natural number, 0, or the negative of a natural number. That means that
is a natural number, 0, or the negative of a natural number. That means that ![]() is defined for any integer
is defined for any integer ![]() Also, the product and quotient rules and all of the rules we will look at soon hold for any integer
Also, the product and quotient rules and all of the rules we will look at soon hold for any integer ![]()
The Negative Rule of Exponents
For any nonzero real number ![]() and natural number
and natural number ![]() the negative rule of exponents states that
the negative rule of exponents states that
Using the Negative Exponent Rule
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Try It
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Using the Product and Quotient Rules
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Try It
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Finding the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider ![]() We begin by using the associative and commutative properties of multiplication to regroup the factors.
We begin by using the associative and commutative properties of multiplication to regroup the factors.

In other words, ![]()
The Power of a Product Rule of Exponents
For any real numbers ![]() and
and ![]() and any integer
and any integer ![]() the power of a product rule of exponents states that
the power of a product rule of exponents states that
Using the Power of a Product Rule
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
Show Solution
Use the product and quotient rules and the new definitions to simplify each expression.
Try It
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
Show Solution
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.
Let’s rewrite the original problem differently and look at the result.
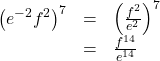
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.

The Power of a Quotient Rule of Exponents
For any real numbers ![]() and
and ![]() and any integer
and any integer ![]() the power of a quotient rule of exponents states that
the power of a quotient rule of exponents states that
Using the Power of a Quotient Rule
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
Show Solution
Try It
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
Show Solution
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
Simplifying Exponential Expressions
Simplify each expression and write the answer with positive exponents only.
Show Solution
Try It
Simplify each expression and write the answer with positive exponents only.
Show Solution
Using Scientific Notation
Recall at the beginning of the section that we found the number ![]() when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about 0.00005 m, and the radius of an electron, which is about 0.00000000000047 m. How can we effectively work read, compare, and calculate with numbers such as these?
when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about 0.00005 m, and the radius of an electron, which is about 0.00000000000047 m. How can we effectively work read, compare, and calculate with numbers such as these?
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10. Count the number of places n that you moved the decimal point. Multiply the decimal number by 10 raised to a power of n. If you moved the decimal left as in a very large number, ![]() is positive. If you moved the decimal right as in a small large number,
is positive. If you moved the decimal right as in a small large number, ![]() is negative.
is negative.
For example, consider the number 2,780,418. Move the decimal left until it is to the right of the first nonzero digit, which is 2.

We obtain 2.780418 by moving the decimal point 6 places to the left. Therefore, the exponent of 10 is 6, and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.
Working with small numbers is similar. Take, for example, the radius of an electron, 0.00000000000047 m. Perform the same series of steps as above, except move the decimal point to the right.

Be careful not to include the leading 0 in your count. We move the decimal point 13 places to the right, so the exponent of 10 is 13. The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.
Scientific Notation
A number is written in scientific notation if it is written in the form ![]() where
where ![]() and
and ![]() is an integer.
is an integer.
Converting Standard Notation to Scientific Notation
Write each number in scientific notation.
- Distance to Andromeda Galaxy from Earth: 24,000,000,000,000,000,000,000 m
- Diameter of Andromeda Galaxy: 1,300,000,000,000,000,000,000 m
- Number of stars in Andromeda Galaxy: 1,000,000,000,000
- Diameter of electron: 0.00000000000094 m
- Probability of being struck by lightning in any single year: 0.00000143
Show Solution
Analysis
Observe that, if the given number is greater than 1, as in examples a–c, the exponent of 10 is positive; and if the number is less than 1, as in examples d–e, the exponent is negative.
Try It
Write each number in scientific notation.
- U.S. national debt per taxpayer (April 2014): $152,000
- World population (April 2014): 7,158,000,000
- World gross national income (April 2014): $85,500,000,000,000
- Time for light to travel 1 m: 0.00000000334 s
- Probability of winning lottery (match 6 of 49 possible numbers): 0.0000000715
Show Solution
Converting from Scientific to Standard Notation
To convert a number in scientific notation to standard notation, simply reverse the process. Move the decimal ![]() places to the right if
places to the right if ![]() is positive or
is positive or ![]() places to the left if
places to the left if ![]() is negative and add zeros as needed. Remember, if
is negative and add zeros as needed. Remember, if ![]() is positive, the value of the number is greater than 1, and if
is positive, the value of the number is greater than 1, and if ![]() is negative, the value of the number is less than one.
is negative, the value of the number is less than one.
Converting Scientific Notation to Standard Notation
Convert each number in scientific notation to standard notation.
Show Solution
Try It
Convert each number in scientific notation to standard notation.
Show Solution
Using Scientific Notation in Applications
Scientific notation, used with the rules of exponents, makes calculating with large or small numbers much easier than doing so using standard notation. For example, suppose we are asked to calculate the number of atoms in 1 L of water. Each water molecule contains 3 atoms (2 hydrogen and 1 oxygen). The average drop of water contains around ![]() molecules of water and 1 L of water holds about
molecules of water and 1 L of water holds about ![]() average drops. Therefore, there are approximately
average drops. Therefore, there are approximately ![]() atoms in 1 L of water. We simply multiply the decimal terms and add the exponents. Imagine having to perform the calculation without using scientific notation!
atoms in 1 L of water. We simply multiply the decimal terms and add the exponents. Imagine having to perform the calculation without using scientific notation!
When performing calculations with scientific notation, be sure to write the answer in proper scientific notation. For example, consider the product ![]() The answer is not in proper scientific notation because 35 is greater than 10. Consider 35 as
The answer is not in proper scientific notation because 35 is greater than 10. Consider 35 as ![]() That adds a ten to the exponent of the answer.
That adds a ten to the exponent of the answer.
Using Scientific Notation
Perform the operations and write the answer in scientific notation.
Show Solution
Try It
Perform the operations and write the answer in scientific notation.
Show Solution
Applying Scientific Notation to Solve Problems
In April 2014, the population of the United States was about 308,000,000 people. The national debt was about $17,547,000,000,000. Write each number in scientific notation, rounding figures to two decimal places, and find the amount of the debt per U.S. citizen. Write the answer in both scientific and standard notations.
Show Solution
The population was ![]()
The national debt was ![]()
To find the amount of debt per citizen, divide the national debt by the number of citizens.
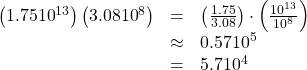
The debt per citizen at the time was about ![]() or $57,000.
or $57,000.
Try It
An average human body contains around 30,000,000,000,000 red blood cells. Each cell measures approximately 0.000008 m long. Write each number in scientific notation and find the total length if the cells were laid end-to-end. Write the answer in both scientific and standard notations.
Show Solution
Number of cells: ![]() length of a cell:
length of a cell: ![]() m; total length:
m; total length: ![]() m or
m or ![]() m.
m.
Access these online resources for additional instruction and practice with exponents and scientific notation.
Key Equations
| Rules of Exponents< For nonzero real numbers |
|
| Product rule | |
| Quotient rule | |
| Power rule | |
| Zero exponent rule | |
| Negative rule | |
| Power of a product rule | |
| Power of a quotient rule | |
Key Concepts
- Products of exponential expressions with the same base can be simplified by adding exponents. See (Figure).
- Quotients of exponential expressions with the same base can be simplified by subtracting exponents. See (Figure).
- Powers of exponential expressions with the same base can be simplified by multiplying exponents. See (Figure).
- An expression with exponent zero is defined as 1. See (Figure).
- An expression with a negative exponent is defined as a reciprocal. See (Figure) and (Figure).
- The power of a product of factors is the same as the product of the powers of the same factors. See (Figure).
- The power of a quotient of factors is the same as the quotient of the powers of the same factors. See (Figure).
- The rules for exponential expressions can be combined to simplify more complicated expressions. See (Figure).
- Scientific notation uses powers of 10 to simplify very large or very small numbers. See (Figure) and (Figure).
- Scientific notation may be used to simplify calculations with very large or very small numbers. See (Figure) and (Figure).
Section Exercises
Verbal
1. Is ![]() the same as
the same as ![]() Explain.
Explain.
Show Solution
No, the two expressions are not the same. An exponent tells how many times you multiply the base. So ![]() is the same as
is the same as ![]() which is 8.
which is 8. ![]() is the same as
is the same as ![]() which is 9.
which is 9.
2. When can you add two exponents?
3. What is the purpose of scientific notation?
Show Solution
It is a method of writing very small and very large numbers.
4. Explain what a negative exponent does.
Numeric
For the following exercises, simplify the given expression. Write answers with positive exponents.
5. ![]()
Show Solution
81
6. ![]()
7. ![]()
Show Solution
243
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
1
14. ![]()
For the following exercises, write each expression with a single base. Do not simplify further. Write answers with positive exponents.
15. ![]()
Show Solution
![]()
16. ![]()
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
For the following exercises, express the decimal in scientific notation.
21. 0.0000314
Show Solution
![]()
22. 148,000,000
For the following exercises, convert each number in scientific notation to standard notation.
23. ![]()
Show Solution
16,000,000,000
24. ![]()
Algebraic
For the following exercises, simplify the given expression. Write answers with positive exponents.
25. ![]()
Show Solution
![]()
26. ![]()
27. ![]()
Show Solution
![]()
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
35. ![]()
Show Solution
![]()
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
41. ![]()
Show Solution
![]()
42. ![]()
43. ![]()
Show Solution
![]()
Real-World Applications
44. To reach escape velocity, a rocket must travel at the rate of ![]() ft/min. Rewrite the rate in standard notation.
ft/min. Rewrite the rate in standard notation.
45. A dime is the thinnest coin in U.S. currency. A dime’s thickness measures ![]() m. Rewrite the number in standard notation.
m. Rewrite the number in standard notation.
Show Solution
0.00135 m
46. The average distance between Earth and the Sun is 92,960,000 mi. Rewrite the distance using scientific notation.
47. A terabyte is made of approximately 1,099,500,000,000 bytes. Rewrite in scientific notation.
Show Solution
![]()
48. The Gross Domestic Product (GDP) for the United States in the first quarter of 2014 was ![]() Rewrite the GDP in standard notation.
Rewrite the GDP in standard notation.
50. One picometer is approximately ![]() in. Rewrite this length using standard notation.
in. Rewrite this length using standard notation.
Show Solution
0.00000000003397 in.
51. The value of the services sector of the U.S. economy in the first quarter of 2012 was $10,633.6 billion. Rewrite this amount in scientific notation.
Technology
52. For the following exercises, use a graphing calculator to simplify. Round the answers to the nearest hundredth.
53. ![]()
Show Solution
12,230,590,464 ![]()
54. ![]()
Extensions
For the following exercises, simplify the given expression. Write answers with positive exponents.
55. ![]()
Show Solution
![]()
56. ![]()
57. ![]()
Show Solution
![]()
58. ![]()
59. ![]()
Show Solution
![]()
60. Avogadro’s constant is used to calculate the number of particles in a mole. A mole is a basic unit in chemistry to measure the amount of a substance. The constant is ![]() Write Avogadro’s constant in standard notation.
Write Avogadro’s constant in standard notation.
61. Planck’s constant is an important unit of measure in quantum physics. It describes the relationship between energy and frequency. The constant is written as ![]() Write Planck’s constant in standard notation.
Write Planck’s constant in standard notation.
Show Solution
0.000000000000000000000000000000000662606957
Glossary
- scientific notation
- a shorthand notation for writing very large or very small numbers in the form
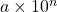 where
where 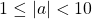 and
and 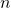 is an integer
is an integer

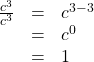






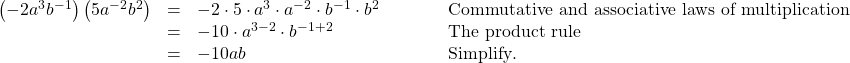


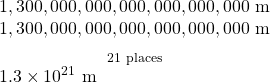
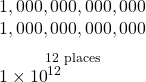

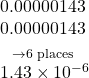
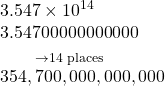
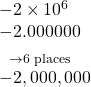
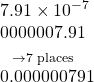
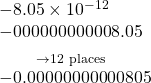
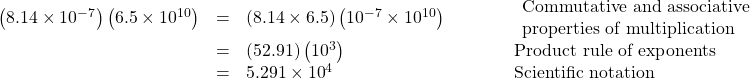

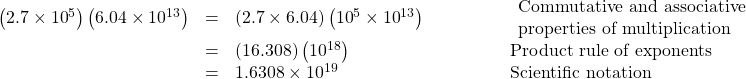

![Rendered by QuickLaTeX.com \begin{array}{ccc}\hfill \left(3.33\times{10}^{4}\right)\left(-1.05\times{10}^{7}\right)\left(5.62\times{10}^{5}\right)& =& \left[3.33\times\left(-1.05\right)\times5.62\right]\left({10}^{4}\times{10}^{7}\times{10}^{5}\right)\hfill \\ & \approx & \left(-19.65\right)\left({10}^{16}\right)\hfill \\ & =& -1.965\times{10}^{17}\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-251c0b0b1f2720130fbaa3724acd79a7_l3.png)
