Chapter 9.7: Exponential and Logarithmic Equations
Learning Objectives
In this section, you will:
- Use like bases to solve exponential equations.
- Use logarithms to solve exponential equations.
- Use the definition of a logarithm to solve logarithmic equations.
- Use the one-to-one property of logarithms to solve logarithmic equations.
- Solve applied problems involving exponential and logarithmic equations.

In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.
Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Using Like Bases to Solve Exponential Equations
The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers ![]()
![]() and
and ![]() where
where ![]()
![]() if and only if
if and only if ![]()
In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.
For example, consider the equation ![]() To solve for
To solve for ![]() we use the division property of exponents to rewrite the right side so that both sides have the common base,
we use the division property of exponents to rewrite the right side so that both sides have the common base, ![]() Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for
Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for ![]()

Using the One-to-One Property of Exponential Functions to Solve Exponential Equations
For any algebraic expressions ![]() and any positive real number
and any positive real number ![]()
How To
Given an exponential equation with the form ![]() where
where ![]() and
and ![]() are algebraic expressions with an unknown, solve for the unknown.
are algebraic expressions with an unknown, solve for the unknown.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form
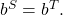
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation,
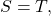 for the unknown.
for the unknown.
Solving an Exponential Equation with a Common Base
Solve ![]()
Show Solution
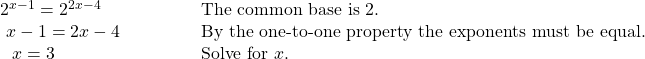
Try It
Solve ![]()
Show Solution
![]()
Rewriting Equations So All Powers Have the Same Base
Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.
For example, consider the equation ![]() We can rewrite both sides of this equation as a power of
We can rewrite both sides of this equation as a power of ![]() Then we apply the rules of exponents, along with the one-to-one property, to solve for
Then we apply the rules of exponents, along with the one-to-one property, to solve for ![]()

How To
Given an exponential equation with unlike bases, use the one-to-one property to solve it.
- Rewrite each side in the equation as a power with a common base.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form
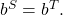
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation,
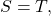 for the unknown.
for the unknown.
Solving Equations by Rewriting Them to Have a Common Base
Solve ![]()
Show Solution

Try It
Solve ![]()
Show Solution
![]()
Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base
Solve ![]()
Show Solution
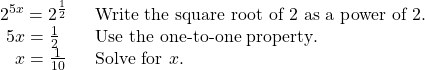
Try It
Solve ![]()
Show Solution
![]()
Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?
No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.
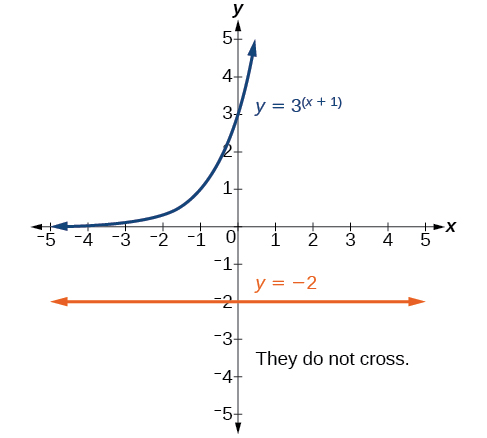
Solving an Equation with Positive and Negative Powers
Solve ![]()
Show Solution
This equation has no solution. There is no real value of ![]() that will make the equation a true statement because any power of a positive number is positive.
that will make the equation a true statement because any power of a positive number is positive.
Analysis
(Figure) shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.
Try It
Solve ![]()
Show Solution
The equation has no solution.
Solving Exponential Equations Using Logarithms
Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since ![]() is equivalent to
is equivalent to ![]() we may apply logarithms with the same base on both sides of an exponential equation.
we may apply logarithms with the same base on both sides of an exponential equation.
How To
Given an exponential equation in which a common base cannot be found, solve for the unknown.
- Apply the logarithm of both sides of the equation.
- If one of the terms in the equation has base 10, use the common logarithm.
- If none of the terms in the equation has base 10, use the natural logarithm.
- Use the rules of logarithms to solve for the unknown.
Solving an Equation Containing Powers of Different Bases
Solve ![]()
Show Solution

Try It
Solve ![]()
Show Solution
![]()
Is there any way to solve ![]()
Yes. The solution is ![]()
Equations Containing e
One common type of exponential equations are those with base ![]() This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base
This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base ![]() on either side, we can use the natural logarithm to solve it.
on either side, we can use the natural logarithm to solve it.
How To
Given an equation of the form ![]() solve for
solve for ![]()
- Divide both sides of the equation by
- Apply the natural logarithm of both sides of the equation.
- Divide both sides of the equation by

Solve an Equation of the Form y = Aekt
Solve ![]()
Show Solution
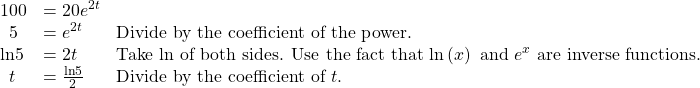
Analysis
Using laws of logs, we can also write this answer in the form ![]() If we want a decimal approximation of the answer, we use a calculator.
If we want a decimal approximation of the answer, we use a calculator.
Try It
Solve ![]()
Show Solution
![]() or
or ![]()
Does every equation of the form ![]() have a solution?
have a solution?
No. There is a solution when ![]() and when
and when ![]() and
and ![]() are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is
are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is ![]()
Solving an Equation That Can Be Simplified to the Form y = Aekt
Solve ![]()
Show Solution

Try It
Solve ![]()
Show Solution
![]()
Extraneous Solutions
Sometimes the methods used to solve an equation introduce an extraneous solution, which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.
Solving Exponential Functions in Quadratic Form
Solve ![]()
Show Solution

Analysis
When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation ![]() because a positive number never equals a negative number. The solution
because a positive number never equals a negative number. The solution ![]() is not a real number, and in the real number system this solution is rejected as an extraneous solution.
is not a real number, and in the real number system this solution is rejected as an extraneous solution.
Try It
Solve ![]()
Show Solution
![]()
Does every logarithmic equation have a solution?
No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.
Using the Definition of a Logarithm to Solve Logarithmic Equations
We have already seen that every logarithmic equation ![]() is equivalent to the exponential equation
is equivalent to the exponential equation ![]() We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation ![]() To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for
To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for ![]()

Using the Definition of a Logarithm to Solve Logarithmic Equations
For any algebraic expression ![]() and real numbers
and real numbers ![]() and
and ![]() where
where ![]()
Using Algebra to Solve a Logarithmic Equation
Solve ![]()
Show Solution

Try It
Solve ![]()
Show Solution
![]()
Using Algebra Before and After Using the Definition of the Natural Logarithm
Solve ![]()
Show Solution

Try It
Solve ![]()
Show Solution
![]()
Using a Graph to Understand the Solution to a Logarithmic Equation
Solve ![]()
Show Solution
(Figure) represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words ![]() A calculator gives a better approximation:
A calculator gives a better approximation: ![]()
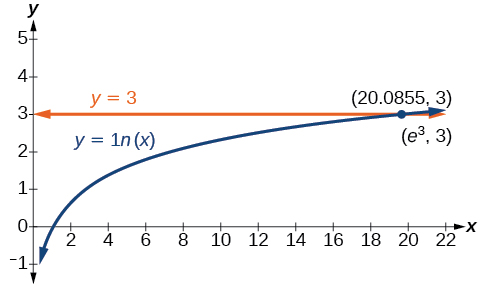
 and
and  cross at the point
cross at the point 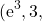 which is approximately (20.0855, 3).
which is approximately (20.0855, 3).Try It
Use a graphing calculator to estimate the approximate solution to the logarithmic equation ![]() to 2 decimal places.
to 2 decimal places.
Show Solution
![]()
Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers ![]()
![]()
![]() and any positive real number
and any positive real number ![]() where
where ![]()
For example,
So, if ![]() then we can solve for
then we can solve for ![]() and we get
and we get ![]() To check, we can substitute
To check, we can substitute ![]() into the original equation:
into the original equation: ![]() In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
For example, consider the equation ![]() To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for
To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for ![]()

To check the result, substitute ![]() into
into ![]()

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
For any algebraic expressions ![]() and
and ![]() and any positive real number
and any positive real number ![]() where
where ![]()
Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.
How To
Given an equation containing logarithms, solve it using the one-to-one property.
- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form
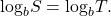
- Use the one-to-one property to set the arguments equal.
- Solve the resulting equation,
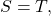 for the unknown.
for the unknown.
Solving an Equation Using the One-to-One Property of Logarithms
Solve ![]()
Show Solution

Analysis
There are two solutions: ![]() or
or ![]() The solution
The solution ![]() is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.
is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.
Try It
Solve ![]()
Show Solution
![]() or
or ![]()
Solving Applied Problems Using Exponential and Logarithmic Equations
In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.
One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life. (Figure) lists the half-life for several of the more common radioactive substances.
| Substance | Use | Half-life |
|---|---|---|
| gallium-67 | nuclear medicine | 80 hours |
| cobalt-60 | manufacturing | 5.3 years |
| technetium-99m | nuclear medicine | 6 hours |
| americium-241 | construction | 432 years |
| carbon-14 | archeological dating | 5,715 years |
| uranium-235 | atomic power | 703,800,000 years |
We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:
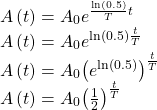
where
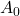 is the amount initially present
is the amount initially present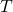 is the half-life of the substance
is the half-life of the substance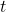 is the time period over which the substance is studied
is the time period over which the substance is studied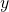 is the amount of the substance present after time
is the amount of the substance present after time 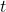
Using the Formula for Radioactive Decay to Find the Quantity of a Substance
How long will it take for ten percent of a 1000-gram sample of uranium-235 to decay?
Show Solution
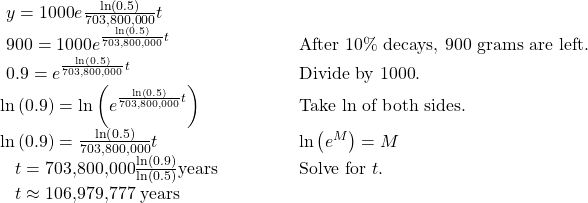
Analysis
Ten percent of 1000 grams is 100 grams. If 100 grams decay, the amount of uranium-235 remaining is 900 grams.
Try It
How long will it take before twenty percent of our 1000-gram sample of uranium-235 has decayed?
Show Solution
![]()
Access these online resources for additional instruction and practice with exponential and logarithmic equations.
Key Equations
| One-to-one property for exponential functions | For any algebraic expressions |
| Definition of a logarithm | For any algebraic expression S and positive real numbers |
| One-to-one property for logarithmic functions | For any algebraic expressions S and T and any positive real number |
Key Concepts
- We can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then we use the fact that exponential functions are one-to-one to set the exponents equal to one another and solve for the unknown.
- When we are given an exponential equation where the bases are explicitly shown as being equal, set the exponents equal to one another and solve for the unknown. See (Figure).
- When we are given an exponential equation where the bases are not explicitly shown as being equal, rewrite each side of the equation as powers of the same base, then set the exponents equal to one another and solve for the unknown. See (Figure), (Figure), and (Figure).
- When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side. See (Figure).
- We can solve exponential equations with base
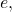 by applying the natural logarithm of both sides because exponential and logarithmic functions are inverses of each other. See (Figure) and (Figure).
by applying the natural logarithm of both sides because exponential and logarithmic functions are inverses of each other. See (Figure) and (Figure). - After solving an exponential equation, check each solution in the original equation to find and eliminate any extraneous solutions. See (Figure).
- When given an equation of the form
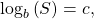 where
where 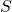 is an algebraic expression, we can use the definition of a logarithm to rewrite the equation as the equivalent exponential equation
is an algebraic expression, we can use the definition of a logarithm to rewrite the equation as the equivalent exponential equation 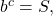 and solve for the unknown. See (Figure) and (Figure).
and solve for the unknown. See (Figure) and (Figure). - We can also use graphing to solve equations with the form
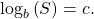 We graph both equations
We graph both equations 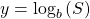 and
and  on the same coordinate plane and identify the solution as the x-value of the intersecting point. See (Figure).
on the same coordinate plane and identify the solution as the x-value of the intersecting point. See (Figure). - When given an equation of the form
 where
where 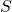 and
and 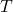 are algebraic expressions, we can use the one-to-one property of logarithms to solve the equation
are algebraic expressions, we can use the one-to-one property of logarithms to solve the equation 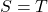 for the unknown. See (Figure).
for the unknown. See (Figure). - Combining the skills learned in this and previous sections, we can solve equations that model real world situations, whether the unknown is in an exponent or in the argument of a logarithm. See (Figure).
Section Exercises
Verbal
1. How can an exponential equation be solved?
Show Solution
Determine first if the equation can be rewritten so that each side uses the same base. If so, the exponents can be set equal to each other. If the equation cannot be rewritten so that each side uses the same base, then apply the logarithm to each side and use properties of logarithms to solve.
2. When does an extraneous solution occur? How can an extraneous solution be recognized?
3. When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?
Show Solution
The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.
Algebraic
For the following exercises, use like bases to solve the exponential equation.
4. ![]()
5. ![]()
Show Solution
![]()
6. ![]()
7. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
For the following exercises, use logarithms to solve.
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
No solution
14. ![]()
15. ![]()
Show Solution
![]()
16. ![]()
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
no solution
26. ![]()
27. ![]()
Show Solution
![]()
For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.
29. ![]()
Show Solution
![]()
30. ![]()
For the following exercises, use the definition of a logarithm to solve the equation.
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
35. ![]()
Show Solution
![]()
For the following exercises, use the one-to-one property of logarithms to solve.
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
No solution
40. ![]()
41. ![]()
Show Solution
No solution
42. ![]()
43. ![]()
Show Solution
![]()
For the following exercises, solve each equation for ![]()
44. ![]()
45. ![]()
Show Solution
![]()
46. ![]()
47. ![]()
Show Solution
48. ![]()
49. ![]()
Show Solution
![]()
50. ![]()
Graphical
For the following exercises, solve the equation for ![]() if there is a solution. Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.
if there is a solution. Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.
51. ![]()
Show Solution
![]()

53. ![]()
Show Solution
![]()

54. ![]()
55. ![]()
Show Solution
![]()

56. ![]()
57. ![]()
Show Solution
![]()

58. ![]()
Show Solution
No solution

60. ![]()
61. ![]()
Show Solution
![]()

62. ![]()
63. ![]()
Show Solution
![]()

64. ![]()
For the following exercises, solve for the indicated value, and graph the situation showing the solution point.
65. An account with an initial deposit of ![]() earns
earns ![]() annual interest, compounded continuously. How much will the account be worth after 20 years?
annual interest, compounded continuously. How much will the account be worth after 20 years?
Show Solution
about ![]()

66. The formula for measuring sound intensity in decibels ![]() is defined by the equation
is defined by the equation ![]() where
where ![]() is the intensity of the sound in watts per square meter and
is the intensity of the sound in watts per square meter and ![]() is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of
is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of ![]() watts per square meter?
watts per square meter?
67. The population of a small town is modeled by the equation ![]() where
where ![]() is measured in years. In approximately how many years will the town’s population reach
is measured in years. In approximately how many years will the town’s population reach ![]()
Show Solution
about 5 years

Technology
For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate ![]() to 3 decimal places.
to 3 decimal places.
68. ![]() using the common log.
using the common log.
69. ![]() using the natural log
using the natural log
Show Solution
![]()
70. ![]() using the common log
using the common log
71. ![]() using the common log
using the common log
Show Solution
![]()
72. ![]() using the natural log
using the natural log
For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.
73. ![]()
Show Solution
![]()
75. ![]()
Show Solution
![]()
76. Atmospheric pressure ![]() in pounds per square inch is represented by the formula
in pounds per square inch is represented by the formula ![]() where
where ![]() is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of
is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of ![]() pounds per square inch? (Hint: there are 5280 feet in a mile)
pounds per square inch? (Hint: there are 5280 feet in a mile)
77. The magnitude M of an earthquake is represented by the equation ![]() where
where ![]() is the amount of energy released by the earthquake in joules and
is the amount of energy released by the earthquake in joules and ![]() is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing
is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing ![]() joules of energy?
joules of energy?
Show Solution
about ![]()
Extensions
78. Use the definition of a logarithm along with the one-to-one property of logarithms to prove that ![]()
79. Recall the formula for continually compounding interest, ![]() Use the definition of a logarithm along with properties of logarithms to solve the formula for time
Use the definition of a logarithm along with properties of logarithms to solve the formula for time ![]() such that
such that ![]() is equal to a single logarithm.
is equal to a single logarithm.
Show Solution
![]()
80. Recall the compound interest formula ![]() Use the definition of a logarithm along with properties of logarithms to solve the formula for time
Use the definition of a logarithm along with properties of logarithms to solve the formula for time ![]()
81. Newton’s Law of Cooling states that the temperature ![]() of an object at any time t can be described by the equation
of an object at any time t can be described by the equation ![]() where
where ![]() is the temperature of the surrounding environment,
is the temperature of the surrounding environment, ![]() is the initial temperature of the object, and
is the initial temperature of the object, and ![]() is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time
is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time ![]() such that
such that ![]() is equal to a single logarithm.
is equal to a single logarithm.
Show Solution
![]()
Glossary
- extraneous solution
- a solution introduced while solving an equation that does not satisfy the conditions of the original equation

