Chapter 9.9: Fitting Exponential Models to Data
Learning Objectives
In this section, you will:
- Build an exponential model from data.
- Build a logarithmic model from data.
- Build a logistic model from data.
In previous sections of this chapter, we were either given a function explicitly to graph or evaluate, or we were given a set of points that were guaranteed to lie on the curve. Then we used algebra to find the equation that fit the points exactly. In this section, we use a modeling technique called regression analysis to find a curve that models data collected from real-world observations. With regression analysis, we don’t expect all the points to lie perfectly on the curve. The idea is to find a model that best fits the data. Then we use the model to make predictions about future events.
Do not be confused by the word model. In mathematics, we often use the terms function, equation, and model interchangeably, even though they each have their own formal definition. The term model is typically used to indicate that the equation or function approximates a real-world situation.
We will concentrate on three types of regression models in this section: exponential, logarithmic, and logistic. Having already worked with each of these functions gives us an advantage. Knowing their formal definitions, the behavior of their graphs, and some of their real-world applications gives us the opportunity to deepen our understanding. As each regression model is presented, key features and definitions of its associated function are included for review. Take a moment to rethink each of these functions, reflect on the work we’ve done so far, and then explore the ways regression is used to model real-world phenomena.
Building an Exponential Model from Data
As we’ve learned, there are a multitude of situations that can be modeled by exponential functions, such as investment growth, radioactive decay, atmospheric pressure changes, and temperatures of a cooling object. What do these phenomena have in common? For one thing, all the models either increase or decrease as time moves forward. But that’s not the whole story. It’s the way data increase or decrease that helps us determine whether it is best modeled by an exponential equation. Knowing the behavior of exponential functions in general allows us to recognize when to use exponential regression, so let’s review exponential growth and decay.
Recall that exponential functions have the form ![]() or
or ![]() When performing regression analysis, we use the form most commonly used on graphing utilities,
When performing regression analysis, we use the form most commonly used on graphing utilities, ![]() Take a moment to reflect on the characteristics we’ve already learned about the exponential function
Take a moment to reflect on the characteristics we’ve already learned about the exponential function ![]() (assume
(assume ![]() ):
):
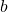 must be greater than zero and not equal to one.
must be greater than zero and not equal to one.- The initial value of the model is
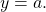
- If
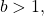 the function models exponential growth. As
the function models exponential growth. As 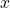 increases, the outputs of the model increase slowly at first, but then increase more and more rapidly, without bound.
increases, the outputs of the model increase slowly at first, but then increase more and more rapidly, without bound. - If
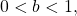 the function models exponential decay. As
the function models exponential decay. As 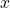 increases, the outputs for the model decrease rapidly at first and then level off to become asymptotic to the x-axis. In other words, the outputs never become equal to or less than zero.
increases, the outputs for the model decrease rapidly at first and then level off to become asymptotic to the x-axis. In other words, the outputs never become equal to or less than zero.
- If
As part of the results, your calculator will display a number known as the correlation coefficient, labeled by the variable ![]() or
or ![]() (You may have to change the calculator’s settings for these to be shown.) The values are an indication of the “goodness of fit” of the regression equation to the data. We more commonly use the value of
(You may have to change the calculator’s settings for these to be shown.) The values are an indication of the “goodness of fit” of the regression equation to the data. We more commonly use the value of ![]() instead of
instead of ![]() but the closer either value is to 1, the better the regression equation approximates the data.
but the closer either value is to 1, the better the regression equation approximates the data.
Exponential Regression
Exponential regression is used to model situations in which growth begins slowly and then accelerates rapidly without bound, or where decay begins rapidly and then slows down to get closer and closer to zero. We use the command “ExpReg” on a graphing utility to fit an exponential function to a set of data points. This returns an equation of the form, ![]()
Note that:
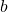 must be non-negative.
must be non-negative.- when
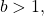 we have an exponential growth model.
we have an exponential growth model. - when
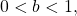 we have an exponential decay model.
we have an exponential decay model.
How To
Given a set of data, perform exponential regression using a graphing utility.
- Use the STAT then EDIT menu to enter given data.
- Clear any existing data from the lists.
- List the input values in the L1 column.
- List the output values in the L2 column.
- Graph and observe a scatter plot of the data using the STATPLOT feature.
- Use ZOOM [9] to adjust axes to fit the data.
- Verify the data follow an exponential pattern.
- Find the equation that models the data.
- Select “ExpReg” from the STAT then CALC menu.
- Use the values returned for a and b to record the model,
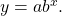
- Graph the model in the same window as the scatterplot to verify it is a good fit for the data.
Using Exponential Regression to Fit a Model to Data
In 2007, a university study was published investigating the crash risk of alcohol impaired driving. Data from 2,871 crashes were used to measure the association of a person’s blood alcohol level (BAC) with the risk of being in an accident. (Figure) shows results from the study[1] . The relative risk is a measure of how many times more likely a person is to crash. So, for example, a person with a BAC of 0.09 is 3.54 times as likely to crash as a person who has not been drinking alcohol.
| BAC | 0 | 0.01 | 0.03 | 0.05 | 0.07 | 0.09 |
| Relative Risk of Crashing | 1 | 1.03 | 1.06 | 1.38 | 2.09 | 3.54 |
| BAC | 0.11 | 0.13 | 0.15 | 0.17 | 0.19 | 0.21 |
| Relative Risk of Crashing | 6.41 | 12.6 | 22.1 | 39.05 | 65.32 | 99.78 |
- Let
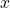 represent the BAC level, and let
represent the BAC level, and let 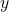 represent the corresponding relative risk. Use exponential regression to fit a model to these data.
represent the corresponding relative risk. Use exponential regression to fit a model to these data. - After 6 drinks, a person weighing 160 pounds will have a BAC of about
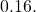 How many times more likely is a person with this weight to crash if they drive after having a 6-pack of beer? Round to the nearest hundredth.
How many times more likely is a person with this weight to crash if they drive after having a 6-pack of beer? Round to the nearest hundredth.
Show Solution
- Using the STAT then EDIT menu on a graphing utility, list the BAC values in L1 and the relative risk values in L2. Then use the STATPLOT feature to verify that the scatterplot follows the exponential pattern shown in (Figure):

Figure 1. Use the “ExpReg” command from the STAT then CALC menu to obtain the exponential model,
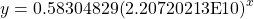
Converting from scientific notation, we have:
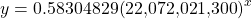
Notice that
 which indicates the model is a good fit to the data. To see this, graph the model in the same window as the scatterplot to verify it is a good fit as shown in (Figure):
which indicates the model is a good fit to the data. To see this, graph the model in the same window as the scatterplot to verify it is a good fit as shown in (Figure):
Figure 2. -
Use the model to estimate the risk associated with a BAC of
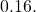 Substitute
Substitute 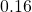 for
for 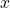 in the model and solve for
in the model and solve for 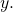

If a 160-pound person drives after having 6 drinks, he or she is about 26.35 times more likely to crash than if driving while sober.
Try It
(Figure) shows a recent graduate’s credit card balance each month after graduation.
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Debt ($) | 620.00 | 761.88 | 899.80 | 1039.93 | 1270.63 | 1589.04 | 1851.31 | 2154.92 |
- Use exponential regression to fit a model to these data.
- If spending continues at this rate, what will the graduate’s credit card debt be one year after graduating?
Show Solution
- The exponential regression model that fits these data is

- If spending continues at this rate, the graduate’s credit card debt will be $4,499.38 after one year.
Is it reasonable to assume that an exponential regression model will represent a situation indefinitely?
No. Remember that models are formed by real-world data gathered for regression. It is usually reasonable to make estimates within the interval of original observation (interpolation). However, when a model is used to make predictions, it is important to use reasoning skills to determine whether the model makes sense for inputs far beyond the original observation interval (extrapolation).
Building a Logarithmic Model from Data
Just as with exponential functions, there are many real-world applications for logarithmic functions: intensity of sound, pH levels of solutions, yields of chemical reactions, production of goods, and growth of infants. As with exponential models, data modeled by logarithmic functions are either always increasing or always decreasing as time moves forward. Again, it is the way they increase or decrease that helps us determine whether a logarithmic model is best.
Recall that logarithmic functions increase or decrease rapidly at first, but then steadily slow as time moves on. By reflecting on the characteristics we’ve already learned about this function, we can better analyze real world situations that reflect this type of growth or decay. When performing logarithmic regression analysis, we use the form of the logarithmic function most commonly used on graphing utilities, ![]() For this function
For this function
- All input values,
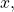 must be greater than zero.
must be greater than zero. - The point
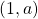 is on the graph of the model.
is on the graph of the model. - If
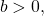 the model is increasing. Growth increases rapidly at first and then steadily slows over time.
the model is increasing. Growth increases rapidly at first and then steadily slows over time. - If
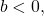 the model is decreasing. Decay occurs rapidly at first and then steadily slows over time.
the model is decreasing. Decay occurs rapidly at first and then steadily slows over time.
Logarithmic Regression
Logarithmic regression is used to model situations where growth or decay accelerates rapidly at first and then slows over time. We use the command “LnReg” on a graphing utility to fit a logarithmic function to a set of data points. This returns an equation of the form,
Note that
- all input values,
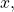 must be non-negative.
must be non-negative. - when
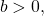 the model is increasing.
the model is increasing. - when
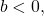 the model is decreasing.
the model is decreasing.
How To
Given a set of data, perform logarithmic regression using a graphing utility.
- Use the STAT then EDIT menu to enter given data.
- Clear any existing data from the lists.
- List the input values in the L1 column.
- List the output values in the L2 column.
- Graph and observe a scatter plot of the data using the STATPLOT feature.
- Use ZOOM [9] to adjust axes to fit the data.
- Verify the data follow a logarithmic pattern.
- Find the equation that models the data.
- Select “LnReg” from the STAT then CALC menu.
- Use the values returned for a and b to record the model,

- Graph the model in the same window as the scatterplot to verify it is a good fit for the data.
Using Logarithmic Regression to Fit a Model to Data
Due to advances in medicine and higher standards of living, life expectancy has been increasing in most developed countries since the beginning of the 20th century.
(Figure) shows the average life expectancies, in years, of Americans from 1900–2010[2] .
| Year | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 |
| Life Expectancy(Years) | 47.3 | 50.0 | 54.1 | 59.7 | 62.9 | 68.2 |
| Year | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| Life Expectancy(Years) | 69.7 | 70.8 | 73.7 | 75.4 | 76.8 | 78.7 |
- Let
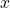 represent time in decades starting with
represent time in decades starting with 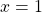 for the year 1900,
for the year 1900,  for the year 1910, and so on. Let
for the year 1910, and so on. Let 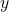 represent the corresponding life expectancy. Use logarithmic regression to fit a model to these data.
represent the corresponding life expectancy. Use logarithmic regression to fit a model to these data. - Use the model to predict the average American life expectancy for the year 2030.
Show Solution
- Using the STAT then EDIT menu on a graphing utility, list the years using values 1–12 in L1 and the corresponding life expectancy in L2. Then use the STATPLOT feature to verify that the scatterplot follows a logarithmic pattern as shown in (Figure):

Figure 3. Use the “LnReg” command from the STAT then CALC menu to obtain the logarithmic model,

Next, graph the model in the same window as the scatterplot to verify it is a good fit as shown in (Figure):

Figure 4. - To predict the life expectancy of an American in the year 2030, substitute
 for the in the model and solve for
for the in the model and solve for 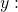

If life expectancy continues to increase at this pace, the average life expectancy of an American will be 79.1 by the year 2030.
Try It
Sales of a video game released in the year 2000 took off at first, but then steadily slowed as time moved on. (Figure) shows the number of games sold, in thousands, from the years 2000–2010.
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Number Sold (thousands) | 142 | 149 | 154 | 155 | 159 | 161 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | – |
| Number Sold (thousands) | 163 | 164 | 164 | 166 | 167 | – |
- Let
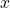 represent time in years starting with
represent time in years starting with 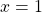 for the year 2000. Let
for the year 2000. Let 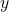 represent the number of games sold in thousands. Use logarithmic regression to fit a model to these data.
represent the number of games sold in thousands. Use logarithmic regression to fit a model to these data. - If games continue to sell at this rate, how many games will sell in 2015? Round to the nearest thousand.
Show Solution
- The logarithmic regression model that fits these data is
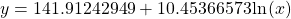
- If sales continue at this rate, about 171,000 games will be sold in the year 2015.
Building a Logistic Model from Data
Like exponential and logarithmic growth, logistic growth increases over time. One of the most notable differences with logistic growth models is that, at a certain point, growth steadily slows and the function approaches an upper bound, or limiting value. Because of this, logistic regression is best for modeling phenomena where there are limits in expansion, such as availability of living space or nutrients.
It is worth pointing out that logistic functions actually model resource-limited exponential growth. There are many examples of this type of growth in real-world situations, including population growth and spread of disease, rumors, and even stains in fabric. When performing logistic regression analysis, we use the form most commonly used on graphing utilities:
Recall that:
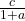 is the initial value of the model.
is the initial value of the model.- when
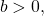 the model increases rapidly at first until it reaches its point of maximum growth rate,
the model increases rapidly at first until it reaches its point of maximum growth rate, 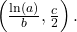 At that point, growth steadily slows and the function becomes asymptotic to the upper bound
At that point, growth steadily slows and the function becomes asymptotic to the upper bound 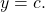

is the limiting value, sometimes called the carrying capacity, of the model.
Logistic Regression
Logistic regression is used to model situations where growth accelerates rapidly at first and then steadily slows to an upper limit. We use the command “Logistic” on a graphing utility to fit a logistic function to a set of data points. This returns an equation of the form
Note that
- The initial value of the model is
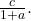
- Output values for the model grow closer and closer to
 as time increases.
as time increases.
How To
Given a set of data, perform logistic regression using a graphing utility.
- Use the STAT then EDIT menu to enter given data.
- Clear any existing data from the lists.
- List the input values in the L1 column.
- List the output values in the L2 column.
- Graph and observe a scatter plot of the data using the STATPLOT feature.
- Use ZOOM [9] to adjust axes to fit the data.
- Verify the data follow a logistic pattern.
- Find the equation that models the data.
- Select “Logistic” from the STAT then CALC menu.
- Use the values returned for
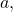
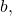 and
and  to record the model,
to record the model, 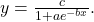
- Graph the model in the same window as the scatterplot to verify it is a good fit for the data.
Using Logistic Regression to Fit a Model to Data
Mobile telephone service has increased rapidly in America since the mid 1990s. Today, almost all residents have cellular service. (Figure) shows the percentage of Americans with cellular service between the years 1995 and 2012[3] .
| Year | Americans with Cellular Service (%) | Year | Americans with Cellular Service (%) |
|---|---|---|---|
| 1995 | 12.69 | 2004 | 62.852 |
| 1996 | 16.35 | 2005 | 68.63 |
| 1997 | 20.29 | 2006 | 76.64 |
| 1998 | 25.08 | 2007 | 82.47 |
| 1999 | 30.81 | 2008 | 85.68 |
| 2000 | 38.75 | 2009 | 89.14 |
| 2001 | 45.00 | 2010 | 91.86 |
| 2002 | 49.16 | 2011 | 95.28 |
| 2003 | 55.15 | 2012 | 98.17 |
- Let
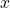 represent time in years starting with
represent time in years starting with  for the year 1995. Let
for the year 1995. Let 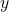 represent the corresponding percentage of residents with cellular service. Use logistic regression to fit a model to these data.
represent the corresponding percentage of residents with cellular service. Use logistic regression to fit a model to these data. - Use the model to calculate the percentage of Americans with cell service in the year 2013. Round to the nearest tenth of a percent.
- Discuss the value returned for the upper limit,
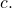 What does this tell you about the model? What would the limiting value be if the model were exact?
What does this tell you about the model? What would the limiting value be if the model were exact?
Show Solution
- Using the STAT then EDIT menu on a graphing utility, list the years using values 0–15 in L1 and the corresponding percentage in L2. Then use the STATPLOT feature to verify that the scatterplot follows a logistic pattern as shown in (Figure):

Figure 5. Use the “Logistic” command from the STAT then CALC menu to obtain the logistic model,
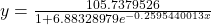
Next, graph the model in the same window as shown in (Figure) the scatterplot to verify it is a good fit:

Figure 6. -
To approximate the percentage of Americans with cellular service in the year 2013, substitute
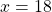 for the in the model and solve for
for the in the model and solve for 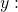

According to the model, about 98.8% of Americans had cellular service in 2013.
- The model gives a limiting value of about 105. This means that the maximum possible percentage of Americans with cellular service would be 105%, which is impossible. (How could over 100% of a population have cellular service?) If the model were exact, the limiting value would be
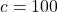 and the model’s outputs would get very close to, but never actually reach 100%. After all, there will always be someone out there without cellular service!
and the model’s outputs would get very close to, but never actually reach 100%. After all, there will always be someone out there without cellular service!
Try It
(Figure) shows the population, in thousands, of harbor seals in the Wadden Sea over the years 1997 to 2012.
| Year | Seal Population (Thousands) | Year | Seal Population (Thousands) |
|---|---|---|---|
| 1997 | 3.493 | 2005 | 19.590 |
| 1998 | 5.282 | 2006 | 21.955 |
| 1999 | 6.357 | 2007 | 22.862 |
| 2000 | 9.201 | 2008 | 23.869 |
| 2001 | 11.224 | 2009 | 24.243 |
| 2002 | 12.964 | 2010 | 24.344 |
| 2003 | 16.226 | 2011 | 24.919 |
| 2004 | 18.137 | 2012 | 25.108 |
- Let
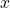 represent time in years starting with
represent time in years starting with  for the year 1997. Let
for the year 1997. Let 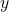 represent the number of seals in thousands. Use logistic regression to fit a model to these data.
represent the number of seals in thousands. Use logistic regression to fit a model to these data. - Use the model to predict the seal population for the year 2020.
- To the nearest whole number, what is the limiting value of this model?
Show Solution
- The logistic regression model that fits these data is
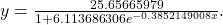
- If the population continues to grow at this rate, there will be about
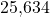 seals in 2020.
seals in 2020. - To the nearest whole number, the carrying capacity is 25,657.
Access this online resource for additional instruction and practice with exponential function models.
Visit this website for additional practice questions from Learningpod.
Key Concepts
- Exponential regression is used to model situations where growth begins slowly and then accelerates rapidly without bound, or where decay begins rapidly and then slows down to get closer and closer to zero.
- We use the command “ExpReg” on a graphing utility to fit function of the form
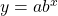 to a set of data points. See (Figure).
to a set of data points. See (Figure). - Logarithmic regression is used to model situations where growth or decay accelerates rapidly at first and then slows over time.
- We use the command “LnReg” on a graphing utility to fit a function of the form
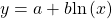 to a set of data points. See (Figure).
to a set of data points. See (Figure). - Logistic regression is used to model situations where growth accelerates rapidly at first and then steadily slows as the function approaches an upper limit.
- We use the command “Logistic” on a graphing utility to fit a function of the form
 to a set of data points. See (Figure).
to a set of data points. See (Figure).
Section Exercises
Verbal
1. What situations are best modeled by a logistic equation? Give an example, and state a case for why the example is a good fit.
Show Solution
Logistic models are best used for situations that have limited values. For example, populations cannot grow indefinitely since resources such as food, water, and space are limited, so a logistic model best describes populations.
2. What is a carrying capacity? What kind of model has a carrying capacity built into its formula? Why does this make sense?
3. What is regression analysis? Describe the process of performing regression analysis on a graphing utility.
Show Solution
Regression analysis is the process of finding an equation that best fits a given set of data points. To perform a regression analysis on a graphing utility, first list the given points using the STAT then EDIT menu. Next graph the scatter plot using the STAT PLOT feature. The shape of the data points on the scatter graph can help determine which regression feature to use. Once this is determined, select the appropriate regression analysis command from the STAT then CALC menu.
4. What might a scatterplot of data points look like if it were best described by a logarithmic model?
5. What does the y-intercept on the graph of a logistic equation correspond to for a population modeled by that equation?
Show Solution
The y-intercept on the graph of a logistic equation corresponds to the initial population for the population model.
Graphical
For the following exercises, match the given function of best fit with the appropriate scatterplot in (Figure) through (Figure). Answer using the letter beneath the matching graph.





6. ![]()
7. ![]()
Show Solution
C
8. ![]()
9. ![]()
Show Solution
B
10. ![]()
Numeric
11. To the nearest whole number, what is the initial value of a population modeled by the logistic equation ![]() What is the carrying capacity?
What is the carrying capacity?
Show Solution
![]() ; 175
; 175
12. Rewrite the exponential model ![]() as an equivalent model with base
as an equivalent model with base ![]() Express the exponent to four significant digits.
Express the exponent to four significant digits.
13. A logarithmic model is given by the equation ![]() To the nearest hundredth, for what value of
To the nearest hundredth, for what value of ![]() does
does ![]()
Show Solution
![]()
14. A logistic model is given by the equation ![]() To the nearest hundredth, for what value of t does
To the nearest hundredth, for what value of t does ![]()
15. What is the y-intercept on the graph of the logistic model given in the previous exercise?
Show Solution
y-intercept: ![]()
Technology
For the following exercises, use this scenario: The population ![]() of a koi pond over
of a koi pond over ![]() months is modeled by the function
months is modeled by the function ![]()
16. Graph the population model to show the population over a span of ![]() years.
years.
17. What was the initial population of koi?
Show Solution
![]() koi
koi
18. How many koi will the pond have after one and a half years?
19. How many months will it take before there are ![]() koi in the pond?
koi in the pond?
Show Solution
about ![]() months.
months.
Use the intersect feature to approximate the number of months it will take before the population of the pond reaches half its carrying capacity.
Show Solution

For the following exercises, use this scenario: The population ![]() of an endangered species habitat for wolves is modeled by the function
of an endangered species habitat for wolves is modeled by the function ![]() where
where ![]() is given in years.
is given in years.
20. Graph the population model to show the population over a span of ![]() years.
years.
21. What was the initial population of wolves transported to the habitat?
Show Solution
![]() wolves
wolves
22. How many wolves will the habitat have after ![]() years?
years?
23. How many years will it take before there are ![]() wolves in the habitat?
wolves in the habitat?
Show Solution
about 5.4 years.
24. Use the intersect feature to approximate the number of years it will take before the population of the habitat reaches half its carrying capacity.
For the following exercises, refer to (Figure).
| x | f(x) |
| 1 | 1125 |
| 2 | 1495 |
| 3 | 2310 |
| 4 | 3294 |
| 5 | 4650 |
| 6 | 6361 |
25. Use a graphing calculator to create a scatter diagram of the data.
Show Solution

26. Use the regression feature to find an exponential function that best fits the data in the table.
27. Write the exponential function as an exponential equation with base ![]()
Show Solution
![]()
28. Graph the exponential equation on the scatter diagram.
29. Use the intersect feature to find the value of ![]() for which
for which ![]()
Show Solution
When ![]()
![]()

For the following exercises, refer to (Figure).
| x | f(x) |
| 1 | 555 |
| 2 | 383 |
| 3 | 307 |
| 4 | 210 |
| 5 | 158 |
| 6 | 122 |
30. Use a graphing calculator to create a scatter diagram of the data.
31. Use the regression feature to find an exponential function that best fits the data in the table.
Show Solution
![]()
32. Write the exponential function as an exponential equation with base ![]()
33. Graph the exponential equation on the scatter diagram.
Show Solution

34. Use the intersect feature to find the value of ![]() for which
for which ![]()
For the following exercises, refer to (Figure).
| x | f(x) |
| 1 | 5.1 |
| 2 | 6.3 |
| 3 | 7.3 |
| 4 | 7.7 |
| 5 | 8.1 |
| 6 | 8.6 |
35. Use a graphing calculator to create a scatter diagram of the data.
Show Solution

36. Use the LOGarithm option of the REGression feature to find a logarithmic function of the form ![]() that best fits the data in the table.
that best fits the data in the table.
37. Use the logarithmic function to find the value of the function when ![]()
Show Solution
![]()
38. Graph the logarithmic equation on the scatter diagram.
39. Use the intersect feature to find the value of ![]() for which
for which ![]()
Show Solution
When ![]()
![]()

For the following exercises, refer to (Figure).
| x | f(x) |
| 1 | 7.5 |
| 2 | 6 |
| 3 | 5.2 |
| 4 | 4.3 |
| 5 | 3.9 |
| 6 | 3.4 |
| 7 | 3.1 |
| 8 | 2.9 |
40. Use a graphing calculator to create a scatter diagram of the data.
41. Use the LOGarithm option of the REGression feature to find a logarithmic function of the form ![]() that best fits the data in the table.
that best fits the data in the table.
Show Solution
![]()
42. Use the logarithmic function to find the value of the function when ![]()
43. Graph the logarithmic equation on the scatter diagram.
Show Solution

44. Use the intersect feature to find the value of ![]() for which
for which ![]()
For the following exercises, refer to (Figure).
| x | f(x) |
| 1 | 8.7 |
| 2 | 12.3 |
| 3 | 15.4 |
| 4 | 18.5 |
| 5 | 20.7 |
| 6 | 22.5 |
| 7 | 23.3 |
| 8 | 24 |
| 9 | 24.6 |
| 10 | 24.8 |
45. Use a graphing calculator to create a scatter diagram of the data.
Show Solution

46. Use the LOGISTIC regression option to find a logistic growth model of the form ![]() that best fits the data in the table.
that best fits the data in the table.
47. Graph the logistic equation on the scatter diagram.
Show Solution

48. To the nearest whole number, what is the predicted carrying capacity of the model?
49. Use the intersect feature to find the value of ![]() for which the model reaches half its carrying capacity.
for which the model reaches half its carrying capacity.
Show Solution
When ![]()
![]()

For the following exercises, refer to (Figure).
| 0 | 12 |
| 2 | 28.6 |
| 4 | 52.8 |
| 5 | 70.3 |
| 7 | 99.9 |
| 8 | 112.5 |
| 10 | 125.8 |
| 11 | 127.9 |
| 15 | 135.1 |
| 17 | 135.9 |
50. Use a graphing calculator to create a scatter diagram of the data.
51. Use the LOGISTIC regression option to find a logistic growth model of the form ![]() that best fits the data in the table.
that best fits the data in the table.
Show Solution
![]()
52. Graph the logistic equation on the scatter diagram.
53. To the nearest whole number, what is the predicted carrying capacity of the model?
Show Solution
about ![]()
54. Use the intersect feature to find the value of ![]() for which the model reaches half its carrying capacity.
for which the model reaches half its carrying capacity.
Extensions
55. Recall that the general form of a logistic equation for a population is given by ![]() such that the initial population at time
such that the initial population at time ![]() is
is ![]() Show algebraically that
Show algebraically that ![]()
Show Solution
Working with the left side of the equation, we see that it can be rewritten as ![]()
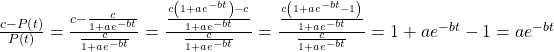
Working with the right side of the equation we show that it can also be rewritten as ![]() But first note that when
But first note that when ![]()
![]() Therefore,
Therefore,
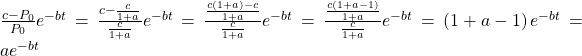
Thus, ![]()
56. Use a graphing utility to find an exponential regression formula ![]() and a logarithmic regression formula
and a logarithmic regression formula ![]() for the points
for the points ![]() and
and ![]() Round all numbers to 6 decimal places. Graph the points and both formulas along with the line
Round all numbers to 6 decimal places. Graph the points and both formulas along with the line ![]() on the same axis. Make a conjecture about the relationship of the regression formulas.
on the same axis. Make a conjecture about the relationship of the regression formulas.
57. Verify the conjecture made in the previous exercise. Round all numbers to six decimal places when necessary.
Show Solution
First rewrite the exponential with base e: ![]() Then test to verify that
Then test to verify that ![]() taking rounding error into consideration:
taking rounding error into consideration:

58. Find the inverse function ![]() for the logistic function
for the logistic function ![]() Show all steps.
Show all steps.
59. Use the result from the previous exercise to graph the logistic model ![]() along with its inverse on the same axis. What are the intercepts and asymptotes of each function?
along with its inverse on the same axis. What are the intercepts and asymptotes of each function?
Show Solution

The graph of ![]() has a y-intercept at (0, 4) and horizontal asymptotes at y = 0 and y = 20. The graph of
has a y-intercept at (0, 4) and horizontal asymptotes at y = 0 and y = 20. The graph of ![]() has an x– intercept at (4, 0) and vertical asymptotes at x = 0 and x = 20.
has an x– intercept at (4, 0) and vertical asymptotes at x = 0 and x = 20.
Chapter Review Exercises
Exponential Functions
- Determine whether the function
 represents exponential growth, exponential decay, or neither. Explain
represents exponential growth, exponential decay, or neither. Explain
Show Solution
exponential decay; The growth factor, ![]() is between
is between ![]() and
and ![]()
2. The population of a herd of deer is represented by the function ![]() where
where ![]() is given in years. To the nearest whole number, what will the herd population be after
is given in years. To the nearest whole number, what will the herd population be after ![]() years?
years?
3. Find an exponential equation that passes through the points ![]() and
and ![]()
Show Solution
![]()
4. Determine whether (Figure) could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.
| x | 1 | 2 | 3 | 4 |
| f(x) | 3 | 0.9 | 0.27 | 0.081 |
5. A retirement account is opened with an initial deposit of $8,500 and earns ![]() interest compounded monthly. What will the account be worth in
interest compounded monthly. What will the account be worth in ![]() years?
years?
Show Solution
![]()
6. Hsu-Mei wants to save $5,000 for a down payment on a car. To the nearest dollar, how much will she need to invest in an account now with ![]() APR, compounded daily, in order to reach her goal in
APR, compounded daily, in order to reach her goal in ![]() years?
years?
7. Does the equation ![]() represent continuous growth, continuous decay, or neither? Explain.
represent continuous growth, continuous decay, or neither? Explain.
Show Solution
continuous decay; the growth rate is negative.
8. Suppose an investment account is opened with an initial deposit of ![]() earning
earning ![]() interest, compounded continuously. How much will the account be worth after
interest, compounded continuously. How much will the account be worth after ![]() years?
years?
Graphs of Exponential Functions
9. Graph the function ![]() State the domain and range and give the y-intercept.
State the domain and range and give the y-intercept.
Show Solution
domain: all real numbers; range: all real numbers strictly greater than zero; y-intercept: (0, 3.5);

10. Graph the function ![]() and its reflection about the y-axis on the same axes, and give the y-intercept.
and its reflection about the y-axis on the same axes, and give the y-intercept.
11. The graph of ![]() is reflected about the y-axis and stretched vertically by a factor of
is reflected about the y-axis and stretched vertically by a factor of ![]() What is the equation of the new function,
What is the equation of the new function, ![]() State its y-intercept, domain, and range.
State its y-intercept, domain, and range.
Show Solution
![]() y-intercept:
y-intercept: ![]() Domain: all real numbers; Range: all real numbers greater than
Domain: all real numbers; Range: all real numbers greater than ![]()
12. The graph below shows transformations of the graph of ![]() What is the equation for the transformation?
What is the equation for the transformation?

Logarithmic Functions
13. Rewrite ![]() as an equivalent exponential equation.
as an equivalent exponential equation.
Show Solution
![]()
14. Rewrite ![]() as an equivalent exponential equation.
as an equivalent exponential equation.
15. Rewrite ![]() as an equivalent logarithmic equation.
as an equivalent logarithmic equation.
Show Solution
![]()
16. Rewrite ![]() as an equivalent logarithmic equation.
as an equivalent logarithmic equation.
17. Solve for x if ![]() by converting to exponential form.
by converting to exponential form.
Show Solution
![]()
18. Evaluate ![]() without using a calculator.
without using a calculator.
19. Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
![]()
20. Evaluate ![]() using a calculator. Round to the nearest thousandth.
using a calculator. Round to the nearest thousandth.
21. Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
![]()
22. Evaluate ![]() using a calculator. Round to the nearest thousandth.
using a calculator. Round to the nearest thousandth.
Graphs of Logarithmic Functions
23. Graph the function ![]()
Show Solution

24. Graph the function ![]()
25. State the domain, vertical asymptote, and end behavior of the function ![]()
Show Solution
Domain: ![]() Vertical asymptote:
Vertical asymptote: ![]() End behavior: as
End behavior: as ![]() and as
and as ![]()
Logarithmic Properties
26. Rewrite ![]() in expanded form.
in expanded form.
27. Rewrite ![]() in compact form.
in compact form.
Show Solution
![]()
28. Rewrite ![]() in expanded form.
in expanded form.
29. Rewrite ![]() in compact form.
in compact form.
Show Solution
![]()
30. Rewrite ![]() as a product.
as a product.
31. Rewrite ![]() as a single logarithm.
as a single logarithm.
Show Solution
![]()
32.Use properties of logarithms to expand ![]()
33.Use properties of logarithms to expand ![]()
Show Solution
![]()
34. Condense the expression ![]() to a single logarithm.
to a single logarithm.
35. Condense the expression ![]() to a single logarithm.
to a single logarithm.
Show Solution
![]()
36. Rewrite ![]() to base
to base ![]()
37. Rewrite ![]() as a logarithm. Then apply the change of base formula to solve for
as a logarithm. Then apply the change of base formula to solve for ![]() using the common log. Round to the nearest thousandth.
using the common log. Round to the nearest thousandth.
Show Solution
![]()
Exponential and Logarithmic Equations
38. Solve ![]() by rewriting each side with a common base.
by rewriting each side with a common base.
39. Solve ![]() by rewriting each side with a common base.
by rewriting each side with a common base.
Show Solution
![]()
40. Use logarithms to find the exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
41. Use logarithms to find the exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
Show Solution
no solution
42. Find the exact solution for ![]() . If there is no solution, write no solution.
. If there is no solution, write no solution.
43. Find the exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
Show Solution
no solution
44. Find the exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
45. Find the exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
Show Solution
![]()
46. Use the definition of a logarithm to solve. ![]()
47. Use the definition of a logarithm to find the exact solution for ![]()
Show Solution
![]()
48. Use the one-to-one property of logarithms to find an exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
49. Use the one-to-one property of logarithms to find an exact solution for ![]() If there is no solution, write no solution.
If there is no solution, write no solution.
Show Solution
![]()
50. The formula for measuring sound intensity in decibels ![]() is defined by the equation
is defined by the equation ![]() where
where ![]() is the intensity of the sound in watts per square meter and
is the intensity of the sound in watts per square meter and ![]() is the lowest level of sound that the average person can hear. How many decibels are emitted from a large orchestra with a sound intensity of
is the lowest level of sound that the average person can hear. How many decibels are emitted from a large orchestra with a sound intensity of ![]() watts per square meter?
watts per square meter?
51. The population of a city is modeled by the equation ![]() where
where ![]() is measured in years. If the city continues to grow at this rate, how many years will it take for the population to reach one million?
is measured in years. If the city continues to grow at this rate, how many years will it take for the population to reach one million?
Show Solution
about ![]() years
years
52. Find the inverse function ![]() for the exponential function
for the exponential function ![]()
53. Find the inverse function ![]() for the logarithmic function
for the logarithmic function ![]()
Show Solution
![]()
Exponential and Logarithmic Models
For the following exercises, use this scenario: A doctor prescribes ![]() milligrams of a therapeutic drug that decays by about
milligrams of a therapeutic drug that decays by about ![]() each hour.
each hour.
54. To the nearest minute, what is the half-life of the drug?
55. Write an exponential model representing the amount of the drug remaining in the patient’s system after ![]() hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after
hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after ![]() hours. Round to the nearest hundredth of a gram.
hours. Round to the nearest hundredth of a gram.
Show Solution
![]()
For the following exercises, use this scenario: A soup with an internal temperature of ![]() Fahrenheit was taken off the stove to cool in a
Fahrenheit was taken off the stove to cool in a ![]() room. After fifteen minutes, the internal temperature of the soup was
room. After fifteen minutes, the internal temperature of the soup was ![]()
56. Use Newton’s Law of Cooling to write a formula that models this situation.
57. How many minutes will it take the soup to cool to ![]()
Show Solution
about ![]() minutes
minutes
For the following exercises, use this scenario: The equation ![]() models the number of people in a school who have heard a rumor after
models the number of people in a school who have heard a rumor after ![]() days.
days.
58. How many people started the rumor?
59. To the nearest tenth, how many days will it be before the rumor spreads to half the carrying capacity?
Show Solution
about ![]() days
days
60. What is the carrying capacity?
For the following exercises, enter the data from each table into a graphing calculator and graph the resulting scatter plots. Determine whether the data from the table would likely represent a function that is linear, exponential, or logarithmic.
61.
| x | f(x) |
| 1 | 3.05 |
| 2 | 4.42 |
| 3 | 6.4 |
| 4 | 9.28 |
| 5 | 13.46 |
| 6 | 19.52 |
| 7 | 28.3 |
| 8 | 41.04 |
| 9 | 59.5 |
| 10 | 86.28 |
Show Solution
exponential

62.
| x | f(x) |
| 0.5 | 18.05 |
| 1 | 17 |
| 3 | 15.33 |
| 5 | 14.55 |
| 7 | 14.04 |
| 10 | 13.5 |
| 12 | 13.22 |
| 13 | 13.1 |
| 15 | 12.88 |
| 17 | 12.69 |
| 20 | 12.45 |
63. Find a formula for an exponential equation that goes through the points ![]() and
and ![]() Then express the formula as an equivalent equation with base e.
Then express the formula as an equivalent equation with base e.
Show Solution
![]()
![]()
Fitting Exponential Models to Data
64. What is the carrying capacity for a population modeled by the logistic equation ![]() What is the initial population for the model?
What is the initial population for the model?
65. The population of a culture of bacteria is modeled by the logistic equation ![]() where
where ![]() is in days. To the nearest tenth, how many days will it take the culture to reach
is in days. To the nearest tenth, how many days will it take the culture to reach ![]() of its carrying capacity?
of its carrying capacity?
Show Solution
about ![]() days
days
For the following exercises, use a graphing utility to create a scatter diagram of the data given in the table. Observe the shape of the scatter diagram to determine whether the data is best described by an exponential, logarithmic, or logistic model. Then use the appropriate regression feature to find an equation that models the data. When necessary, round values to five decimal places.
66.
| x | f(x) |
| 1 | 409.4 |
| 2 | 260.7 |
| 3 | 170.4 |
| 4 | 110.6 |
| 5 | 74 |
| 6 | 44.7 |
| 7 | 32.4 |
| 8 | 19.5 |
| 9 | 12.7 |
| 10 | 8.1 |
67.
| x | f(x) |
| 0.15 | 36.21 |
| 0.25 | 28.88 |
| 0.5 | 24.39 |
| 0.75 | 18.28 |
| 1 | 16.5 |
| 1.5 | 12.99 |
| 2 | 9.91 |
| 2.25 | 8.57 |
| 2.75 | 7.23 |
| 3 | 5.99 |
| 3.5 | 4.81 |
Show Solution
logarithmic; ![]()

68.
| x | f(x) |
| 0 | 9 |
| 2 | 22.6 |
| 4 | 44.2 |
| 5 | 62.1 |
| 7 | 96.9 |
| 8 | 113.4 |
| 10 | 133.4 |
| 11 | 137.6 |
| 15 | 148.4 |
| 17 | 149.3 |

