Chapter 4.8: Parametric Equations: Graphs
Learning Objectives
In this section you will:
- Graph plane curves described by parametric equations by plotting points.
- Graph parametric equations.
It is the bottom of the ninth inning, with two outs and two men on base. The home team is losing by two runs. The batter swings and hits the baseball at 140 feet per second and at an angle of approximately ![]() to the horizontal. How far will the ball travel? Will it clear the fence for a game-winning home run? The outcome may depend partly on other factors (for example, the wind), but mathematicians can model the path of a projectile and predict approximately how far it will travel using parametric equations. In this section, we’ll discuss parametric equations and some common applications, such as projectile motion problems.
to the horizontal. How far will the ball travel? Will it clear the fence for a game-winning home run? The outcome may depend partly on other factors (for example, the wind), but mathematicians can model the path of a projectile and predict approximately how far it will travel using parametric equations. In this section, we’ll discuss parametric equations and some common applications, such as projectile motion problems.

Graphing Parametric Equations by Plotting Points
In lieu of a graphing calculator or a computer graphing program, plotting points to represent the graph of an equation is the standard method. As long as we are careful in calculating the values, point-plotting is highly dependable.
How To
Given a pair of parametric equations, sketch a graph by plotting points.
- Construct a table with three columns:
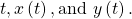
- Evaluate
 and
and 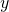 for values of
for values of 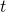 over the interval for which the functions are defined.
over the interval for which the functions are defined. - Plot the resulting pairs
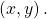
Sketching the Graph of a Pair of Parametric Equations by Plotting Points
Sketch the graph of the parametric equations ![]()
Analysis
As values for ![]() progress in a positive direction from 0 to 5, the plotted points trace out the top half of the parabola. As values of
progress in a positive direction from 0 to 5, the plotted points trace out the top half of the parabola. As values of ![]() become negative, they trace out the lower half of the parabola. There are no restrictions on the domain. The arrows indicate direction according to increasing values of
become negative, they trace out the lower half of the parabola. There are no restrictions on the domain. The arrows indicate direction according to increasing values of ![]() The graph does not represent a function, as it will fail the vertical line test. The graph is drawn in two parts: the positive values for
The graph does not represent a function, as it will fail the vertical line test. The graph is drawn in two parts: the positive values for ![]() and the negative values for
and the negative values for ![]()
Try It
Sketch the graph of the parametric equations ![]()
Show Solution

Sketching the Graph of Trigonometric Parametric Equations
Construct a table of values for the given parametric equations and sketch the graph:
Show Solution
Construct a table like that in (Figure) using angle measure in radians as inputs for ![]() and evaluating
and evaluating ![]() and
and ![]() Using angles with known sine and cosine values for
Using angles with known sine and cosine values for ![]() makes calculations easier.
makes calculations easier.
| 0 | ||
(Figure) shows the graph.

By the symmetry shown in the values of ![]() and
and ![]() we see that the parametric equations represent an ellipse. The ellipse is mapped in a counterclockwise direction as shown by the arrows indicating increasing
we see that the parametric equations represent an ellipse. The ellipse is mapped in a counterclockwise direction as shown by the arrows indicating increasing ![]() values.
values.
Analysis
We have seen that parametric equations can be graphed by plotting points. However, a graphing calculator will save some time and reveal nuances in a graph that may be too tedious to discover using only hand calculations.
Make sure to change the mode on the calculator to parametric (PAR). To confirm, the ![]() window should show
window should show
instead of ![]()
Try It
Graph the parametric equations: ![]()
Show Solution

Graphing Parametric Equations and Rectangular Form Together
Graph the parametric equations ![]() and
and ![]() First, construct the graph using data points generated from the parametric form. Then graph the rectangular form of the equation. Compare the two graphs.
First, construct the graph using data points generated from the parametric form. Then graph the rectangular form of the equation. Compare the two graphs.
Show Solution
Construct a table of values like that in (Figure).
Plot the ![]() values from the table. See (Figure).
values from the table. See (Figure).

Next, translate the parametric equations to rectangular form. To do this, we solve for ![]() in either
in either ![]() or
or ![]() and then substitute the expression for
and then substitute the expression for ![]() in the other equation. The result will be a function
in the other equation. The result will be a function ![]() if solving for
if solving for ![]() as a function of
as a function of ![]() or
or ![]() if solving for
if solving for ![]() as a function of
as a function of ![]()
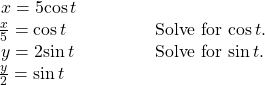
Then, use the Pythagorean Theorem.
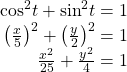
Analysis
In (Figure), the data from the parametric equations and the rectangular equation are plotted together. The parametric equations are plotted in blue; the graph for the rectangular equation is drawn on top of the parametric in a dashed style colored red. Clearly, both forms produce the same graph.

Graphing Parametric Equations and Rectangular Equations on the Coordinate System
Graph the parametric equations ![]() and
and ![]() and the rectangular equivalent
and the rectangular equivalent ![]() on the same coordinate system.
on the same coordinate system.
Show Solution
Construct a table of values for the parametric equations, as we did in the previous example, and graph ![]() on the same grid, as in (Figure).
on the same grid, as in (Figure).

Analysis
With the domain on ![]() restricted, we only plot positive values of
restricted, we only plot positive values of ![]() The parametric data is graphed in blue and the graph of the rectangular equation is dashed in red. Once again, we see that the two forms overlap.
The parametric data is graphed in blue and the graph of the rectangular equation is dashed in red. Once again, we see that the two forms overlap.
Try It
Sketch the graph of the parametric equations ![]() along with the rectangular equation on the same grid.
along with the rectangular equation on the same grid.
Show Solution
The graph of the parametric equations is in red and the graph of the rectangular equation is drawn in blue dots on top of the parametric equations.

Applications of Parametric Equations
Many of the advantages of parametric equations become obvious when applied to solving real-world problems. Although rectangular equations in x and y give an overall picture of an object’s path, they do not reveal the position of an object at a specific time. Parametric equations, however, illustrate how the values of x and y change depending on t, as the location of a moving object at a particular time.
A common application of parametric equations is solving problems involving projectile motion. In this type of motion, an object is propelled forward in an upward direction forming an angle of ![]() to the horizontal, with an initial speed of
to the horizontal, with an initial speed of ![]() and at a height
and at a height ![]() above the horizontal.
above the horizontal.
The path of an object propelled at an inclination of ![]() to the horizontal, with initial speed
to the horizontal, with initial speed ![]() and at a height
and at a height ![]() above the horizontal, is given by
above the horizontal, is given by
where ![]() accounts for the effects of gravity and
accounts for the effects of gravity and ![]() is the initial height of the object. Depending on the units involved in the problem, use
is the initial height of the object. Depending on the units involved in the problem, use ![]() or
or ![]() The equation for
The equation for ![]() gives horizontal distance, and the equation for
gives horizontal distance, and the equation for ![]() gives the vertical distance.
gives the vertical distance.
How To
Given a projectile motion problem, use parametric equations to solve.
- The horizontal distance is given by
 Substitute the initial speed of the object for
Substitute the initial speed of the object for 
- The expression
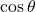 indicates the angle at which the object is propelled. Substitute that angle in degrees for
indicates the angle at which the object is propelled. Substitute that angle in degrees for 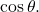
- The vertical distance is given by the formula
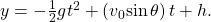 The term
The term 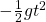 represents the effect of gravity. Depending on units involved, use
represents the effect of gravity. Depending on units involved, use 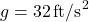 or
or 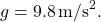 Again, substitute the initial speed for
Again, substitute the initial speed for 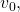 and the height at which the object was propelled for
and the height at which the object was propelled for 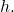
- Proceed by calculating each term to solve for
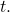
Finding the Parametric Equations to Describe the Motion of a Baseball
Solve the problem presented at the beginning of this section. Does the batter hit the game-winning home run? Assume that the ball is hit with an initial velocity of 140 feet per second at an angle of ![]() to the horizontal, making contact 3 feet above the ground.
to the horizontal, making contact 3 feet above the ground.
- Find the parametric equations to model the path of the baseball.
- Where is the ball after 2 seconds?
- How long is the ball in the air?
- Is it a home run?
Show Solution
-
Use the formulas to set up the equations. The horizontal position is found using the parametric equation for
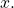 Thus,
Thus,![Rendered by QuickLaTeX.com \begin{array}{l}x=\left({v}_{0}\mathrm{cos}\,\theta \right)t\hfill \\ x=\left(140\mathrm{cos}\left(45°\right)\right)t\hfill \end{array}[/latex</div> The vertical position is found using the parametric equation for [latex]\,y.\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-91ff40ce5104d0240416e6d59ae915f4_l3.png) Thus,
Thus,
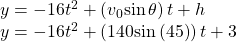
-
Substitute 2 into the equations to find the horizontal and vertical positions of the ball.
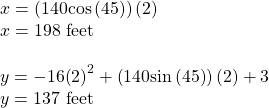
After 2 seconds, the ball is 198 feet away from the batter’s box and 137 feet above the ground.
-
To calculate how long the ball is in the air, we have to find out when it will hit ground, or when
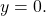 Thus,
Thus,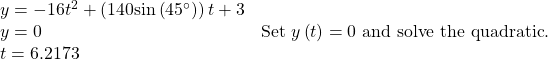
When
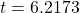 seconds, the ball has hit the ground. (The quadratic equation can be solved in various ways, but this problem was solved using a computer math program.)
seconds, the ball has hit the ground. (The quadratic equation can be solved in various ways, but this problem was solved using a computer math program.) -
We cannot confirm that the hit was a home run without considering the size of the outfield, which varies from field to field. However, for simplicity’s sake, let’s assume that the outfield wall is 400 feet from home plate in the deepest part of the park. Let’s also assume that the wall is 10 feet high. In order to determine whether the ball clears the wall, we need to calculate how high the ball is when x = 400 feet. So we will set x = 400, solve for
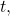 and input
and input 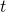 into
into 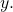
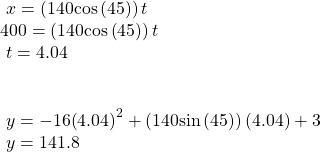
The ball is 141.8 feet in the air when it soars out of the ballpark. It was indeed a home run. See (Figure).

Figure 7.
Access the following online resource for additional instruction and practice with graphs of parametric equations.
Key Concepts
- When there is a third variable, a third parameter on which
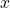 and
and 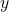 depend, parametric equations can be used.
depend, parametric equations can be used. - To graph parametric equations by plotting points, make a table with three columns labeled
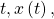 and
and 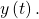 Choose values for
Choose values for 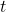 in increasing order. Plot the last two columns for
in increasing order. Plot the last two columns for 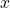 and
and 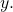 See (Figure) and (Figure).
See (Figure) and (Figure). - When graphing a parametric curve by plotting points, note the associated t-values and show arrows on the graph indicating the orientation of the curve. See (Figure) and (Figure).
- Parametric equations allow the direction or the orientation of the curve to be shown on the graph. Equations that are not functions can be graphed and used in many applications involving motion. See (Figure).
- Projectile motion depends on two parametric equations:
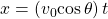 and
and 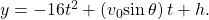 Initial velocity is symbolized as
Initial velocity is symbolized as 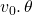 represents the initial angle of the object when thrown, and
represents the initial angle of the object when thrown, and 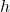 represents the height at which the object is propelled.
represents the height at which the object is propelled.
Section Exercises
Verbal
1. What are two methods used to graph parametric equations?
Show Solution
plotting points with the orientation arrow and a graphing calculator
2. What is one difference in point-plotting parametric equations compared to Cartesian equations?
3. Why are some graphs drawn with arrows?
Show Solution
The arrows show the orientation, the direction of motion according to increasing values of ![]()
4. Name a few common types of graphs of parametric equations.
5. Why are parametric graphs important in understanding projectile motion?
Show Solution
The parametric equations show the different vertical and horizontal motions over time.
Graphical
For the following exercises, graph each set of parametric equations by making a table of values. Include the orientation on the graph.
6. ![]()
| |
|
|
7. ![]()
| |
||||||
| |
||||||
| |
Show Solution

8. ![]()
| |
||||||
| |
||||||
| |
9. ![]()
| |
|||||
| |
|||||
| |
Show Solution

10. ![]()
| |
|||||
| |
|||||
| |
11. ![]()
| |
|||||
| |
|||||
| |
Show Solution

For the following exercises, sketch the curve and include the orientation.
12. ![]()
13. ![]()
Show Solution

14. ![]()
15. ![]()
Show Solution

16. ![]()
17. ![]()
Show Solution

18. ![]()
19. ![]()
Show Solution

20. ![]()
21. ![]()
Show Solution

For the following exercises, graph the equation and include the orientation. Then, write the Cartesian equation.
23. ![]()
Show Solution

24. ![]()
25. ![]()
Show Solution

26. ![]()
27. ![]()
Show Solution

For the following exercises, graph the equation and include the orientation.
29. ![]()
Show Solution

30. ![]()
Show Solution

33. ![]()
Show Solution

For the following exercises, use the parametric equations for integers a and b:
34. Graph on the domain ![]() where
where ![]() and
and ![]() and include the orientation.
and include the orientation.
35. Graph on the domain ![]() where
where ![]() and
and ![]() , and include the orientation.
, and include the orientation.
Show Solution

36. Graph on the domain ![]() where
where ![]() and
and ![]() , and include the orientation.
, and include the orientation.
37. Graph on the domain ![]() where
where ![]() and
and ![]() , and include the orientation.
, and include the orientation.
Show Solution

38. If ![]() is 1 more than
is 1 more than ![]() describe the effect the values of
describe the effect the values of ![]() and
and ![]() have on the graph of the parametric equations.
have on the graph of the parametric equations.
39. Describe the graph if ![]() and
and ![]()
Show Solution
There will be 100 back-and-forth motions.
40. What happens if ![]() is 1 more than
is 1 more than ![]() Describe the graph.
Describe the graph.
41. If the parametric equations ![]() and
and ![]() have the graph of a horizontal parabola opening to the right, what would change the direction of the curve?
have the graph of a horizontal parabola opening to the right, what would change the direction of the curve?
Show Solution
Take the opposite of the ![]() equation.
equation.
For the following exercises, describe the graph of the set of parametric equations.
42. ![]() and
and ![]() is linear
is linear
43. ![]() and
and ![]() is linear
is linear
Show Solution
The parabola opens up.
44. ![]() and
and ![]() is linear
is linear
45. Write the parametric equations of a circle with center ![]() radius 5, and a counterclockwise orientation.
radius 5, and a counterclockwise orientation.
Show Solution
![]()
46. Write the parametric equations of an ellipse with center ![]() major axis of length 10, minor axis of length 6, and a counterclockwise orientation.
major axis of length 10, minor axis of length 6, and a counterclockwise orientation.
For the following exercises, use a graphing utility to graph on the window ![]() by
by ![]() on the domain
on the domain ![]() for the following values of
for the following values of ![]() and
and ![]() , and include the orientation.
, and include the orientation.
47. ![]()
Show Solution

48. ![]()
49. ![]()
Show Solution

50. ![]()
51. ![]()
Show Solution

52. ![]()
Technology
For the following exercises, look at the graphs that were created by parametric equations of the form ![]() Use the parametric mode on the graphing calculator to find the values of
Use the parametric mode on the graphing calculator to find the values of ![]() and
and ![]() to achieve each graph.
to achieve each graph.

Show Solution
![]()
54. 

Show Solution
![]()

For the following exercises, use a graphing utility to graph the given parametric equations.
57. Graph all three sets of parametric equations on the domain ![]()
Show Solution



58. Graph all three sets of parametric equations on the domain ![]()
59. Graph all three sets of parametric equations on the domain ![]()
Show Solution



60. The graph of each set of parametric equations appears to “creep” along one of the axes. What controls which axis the graph creeps along?
61. Explain the effect on the graph of the parametric equation when we switched ![]() and
and ![]() .
.
Show Solution
The ![]() -intercept changes.
-intercept changes.
62. Explain the effect on the graph of the parametric equation when we changed the domain.
Extensions
63. An object is thrown in the air with vertical velocity of 20 ft/s and horizontal velocity of 15 ft/s. The object’s height can be described by the equation ![]() , while the object moves horizontally with constant velocity 15 ft/s. Write parametric equations for the object’s position, and then eliminate time to write height as a function of horizontal position.
, while the object moves horizontally with constant velocity 15 ft/s. Write parametric equations for the object’s position, and then eliminate time to write height as a function of horizontal position.
Show Solution
![]()
64. A skateboarder riding on a level surface at a constant speed of 9 ft/s throws a ball in the air, the height of which can be described by the equation ![]() Write parametric equations for the ball’s position, and then eliminate time to write height as a function of horizontal position.
Write parametric equations for the ball’s position, and then eliminate time to write height as a function of horizontal position.
For the following exercises, use this scenario: A dart is thrown upward with an initial velocity of 65 ft/s at an angle of elevation of 52°. Consider the position of the dart at any time ![]() Neglect air resistance.
Neglect air resistance.
65. Find parametric equations that model the problem situation.
Show Solution
![]()
66. Find all possible values of ![]() that represent the situation.
that represent the situation.
67. When will the dart hit the ground?
Show Solution
approximately 3.2 seconds
68. Find the maximum height of the dart.
69. At what time will the dart reach maximum height?
Show Solution
1.6 seconds
For the following exercises, look at the graphs of each of the four parametric equations. Although they look unusual and beautiful, they are so common that they have names, as indicated in each exercise. Use a graphing utility to graph each on the indicated domain.
70. An epicycloid: ![]() on the domain
on the domain ![]() .
.
71. A hypocycloid: ![]() on the domain
on the domain ![]() .
.
Show Solution

72. A hypotrochoid: ![]() on the domain
on the domain ![]() .
.
73. A rose: ![]() on the domain
on the domain ![]() .
.
Show Solution



