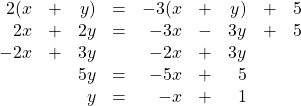Chapter 2.3: Perpendicular and Parallel Lines
Perpendicular, parallel, horizontal, and vertical lines are special lines that have properties unique to each type. Parallel lines, for instance, have the same slope, whereas perpendicular lines are the opposite and have negative reciprocal slopes. Vertical lines have a constant ![]() -value, and horizontal lines have a constant
-value, and horizontal lines have a constant ![]() -value.
-value.
Two equations govern perpendicular and parallel lines:
For parallel lines, the slope of the first line is the same as the slope for the second line. If the slopes of these two lines are called ![]() and
and ![]() , then
, then ![]() .
.
![]()
Perpendicular lines are slightly more difficult to understand. If one line is rising, then the other must be falling, so both lines have slopes going in opposite directions. Thus, the slopes will always be negative to one another. The other feature is that the slope at which one is rising or falling will be exactly flipped for the other one. This means that the slopes will always be negative reciprocals to each other. If the slopes of these two lines are called ![]() and
and ![]() , then
, then ![]() .
.
![]()
Example 1
Find the slopes of the lines that are parallel and perpendicular to ![]()
The parallel line has the identical slope, so its slope is also 3.
The perpendicular line has the negative reciprocal to the other slope, so it is ![]()
Example 2
Find the slopes of the lines that are parallel and perpendicular to ![]()
The parallel line has the identical slope, so its slope is also ![]()
The perpendicular line has the negative reciprocal to the other slope, so it is ![]()
Typically, questions that are asked of students in this topic are written in the form of “Find the equation of a line passing through point ![]() that is perpendicular/parallel to
that is perpendicular/parallel to ![]() .” The first step is to identify the slope that is to be used to solve this equation, and the second is to use the described methods to arrive at the solution like previously done. For instance:
.” The first step is to identify the slope that is to be used to solve this equation, and the second is to use the described methods to arrive at the solution like previously done. For instance:
Example 3
Find the equation of the line passing through the point ![]() that is parallel to the line
that is parallel to the line ![]()
The first step is to identify the slope, which here is the same as in the given equation, ![]() .
.
Now, simply use the methods from before:
![Rendered by QuickLaTeX.com \[\begin{array}{rrl} m&=&\dfrac{y-y_1}{x-x_1} \\ \\ 2&=&\dfrac{y-4}{x-2} \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e68d8ed020443f90ef48ecc18d32eca9_l3.png)
Clearing the fraction by multiplying both sides by ![]() leaves:
leaves:
![]()
Now put this equation in one of the three forms. For this example, use the standard form:
![Rendered by QuickLaTeX.com \[\begin{array}{rrrrrrr} 2x&-&4&=&y&-&4 \\ -y&+&4&&-y&+&4 \\ \midrule 2x&-&y&=&0&& \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-57c9f97b14d79f58b981eea5b5453509_l3.png)
Example 4
Find the equation of the line passing through the point ![]() that is perpendicular to the line
that is perpendicular to the line ![]()
The first step is to identify the slope, which here is the negative reciprocal to the one in the given equation, so ![]()
Now, simply use the methods from before:
![Rendered by QuickLaTeX.com \[\begin{array}{rrl} m&=&\dfrac{y-y_1}{x-x_1} \\ \\ -\dfrac{2}{3}&=&\dfrac{y-3}{x-1} \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8f5d69db28e260f776cdf455a7561743_l3.png)
First, clear the fraction by multiplying both sides by ![]() . This leaves:
. This leaves:
![]()
which reduces to:
![]()
Now put this equation in one of the three forms. For this example, choose the general form:
![Rendered by QuickLaTeX.com \[\begin{array}{rrrrrrrrr} -2x&&&+&2&=&3y&-&9 \\ &&-3y&+&9&&-3y&+&9 \\ \midrule -2x&-&3y&+&11&=&0&& \end{array}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-16b2172993d5b5eb68ee42192bfe3dc8_l3.png)
For the general form, the coefficient in front of the ![]() must be positive. So for this equation, multiply the entire equation by −1 to make
must be positive. So for this equation, multiply the entire equation by −1 to make ![]() positive.
positive.
![]()
![]()
Questions that are looking for the vertical or horizontal line through a given point are the easiest to do and the most commonly confused.
Vertical lines always have a single ![]() -value, yielding an equation like
-value, yielding an equation like ![]()
Horizontal lines always have a single ![]() -value, yielding an equation like
-value, yielding an equation like ![]()
Example 5
Find the equation of the vertical and horizontal lines through the point ![]()
The vertical line has the same ![]() -value, so the equation is
-value, so the equation is ![]() .
.
The horizontal line has the same ![]() -value, so the equation is
-value, so the equation is ![]() .
.
Questions
For questions 1 to 6, find the slope of any line that would be parallel to each given line.
For questions 7 to 12, find the slope of any line that would be perpendicular to each given line.
For questions 13 to 18, write the slope-intercept form of the equation of each line using the given point and line.
- (1, 4) and parallel to
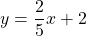
- (5, 2) and perpendicular to

- (3, 4) and parallel to
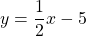
- (1, −1) and perpendicular to

- (2, 3) and parallel to
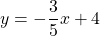
- (−1, 3) and perpendicular to
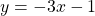
For questions 19 to 24, write the general form of the equation of each line using the given point and line.
- (1, −5) and parallel to
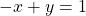
- (1, −2) and perpendicular to
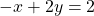
- (5, 2) and parallel to
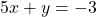
- (1, 3) and perpendicular to
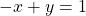
- (4, 2) and parallel to
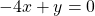
- (3, −5) and perpendicular to
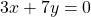
For questions 25 to 36, write the equation of either the horizontal or the vertical line that runs through each point.
- Horizontal line through (4, −3)
- Vertical line through (−5, 2)
- Vertical line through (−3,1)
- Horizontal line through (−4, 0)
- Horizontal line through (−4, −1)
- Vertical line through (2, 3)
- Vertical line through (−2, −1)
- Horizontal line through (−5, −4)
- Horizontal line through (4, 3)
- Vertical line through (−3, −5)
- Vertical line through (5, 2)
- Horizontal line through (5, −1)
Answers to odd questions
For questions 1 to 9, sketch the linear equation using the slope intercept method.
1. ![]()
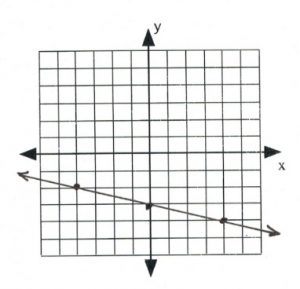
3. ![]()
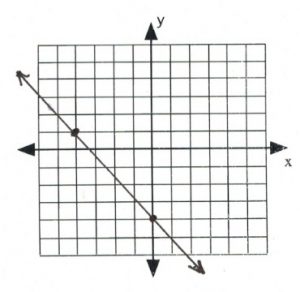
5. ![]()
7. ![]()

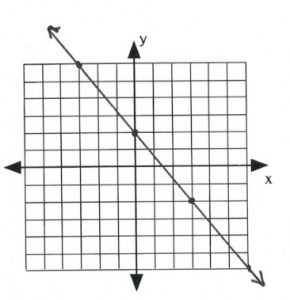
9. ![]()
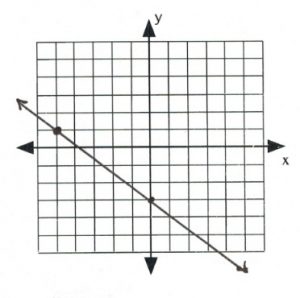
For questions 11 to 19, sketch the linear equation using the ![]() and
and ![]() intercepts.
intercepts.
11. ![]()
13. ![]()

15. ![]()
17. ![]()
19. ![]()
For questions 21 to 27, sketch the linear equation using any method.
21. ![]()
23. ![]()
25. ![]()
27. ![]()
29. 
31. 
33. 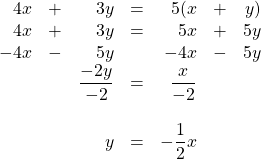
35. 

37. 
39.