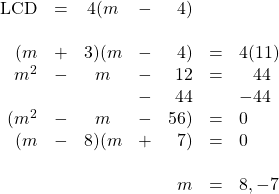Chapter 6.6: Solving Complex Fractions
When solving two or more equated fractions, the easiest solution is to first remove all fractions by multiplying both sides of the equations by the LCD. This strategy is shown in the next examples.
Example 1
Solve ![]() .
.
For these two fractions, the LCD is 3 × 4 = 12. Therefore, we multiply both sides of the equation by 12:
![]()
This reduces the complex fraction to:
![]()
Multiplying this out yields:
![]()
Now just isolate and solve for ![]() :
:
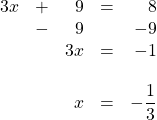
Example 2
Solve ![]() .
.
For these two fractions, the LCD is ![]() . Therefore, both sides of the equation are multiplied by
. Therefore, both sides of the equation are multiplied by ![]() :
:
![]()
This reduces the complex fraction to:
![]()
Multiplying this out yields:
![]()
Now isolate and solve for ![]() :
:
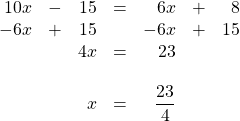
Example 3
Solve ![]() .
.
For these two fractions, the LCD is ![]() . Therefore, multiply both sides of the equation by
. Therefore, multiply both sides of the equation by ![]() :
:
![]()
This reduces the complex fraction to:
![]()
This multiplies out to:
![]()
Now subtract 24 from both sides of the equation to turn this into an equation that can be easily factored:
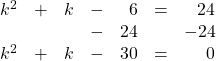
This equation factors to:
![]()
The solutions are:
![]() and
and ![]()
Questions
Solve each of the following complex fractions.
Answers to odd questions
1. 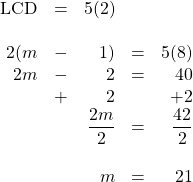
3. 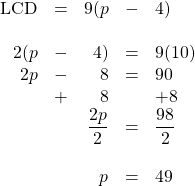
5. 
7. 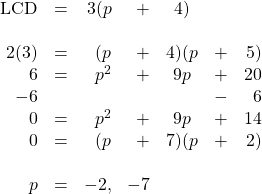
9. 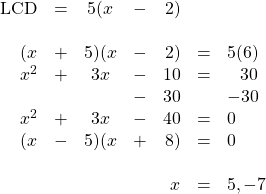
11.