Chapter 1.4: Solve Equations with Fraction or Decimal Coefficients

Learning Objectives

By the end of this section, you will be able to:

  • Solve equations with fraction coefficients
  • Solve equations with decimal coefficients

Solve Equations with Fraction Coefficients

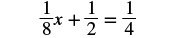Let’s use the General Strategy for Solving Linear Equations introduced earlier to solve the equation \frac{1}{8}\phantom{\rule{0.1em}{0ex}}x+\frac{1}{2}=\frac{1}{4}.

.
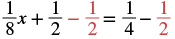To isolate the x term, subtract \frac{1}{2} from both sides. .
Simplify the left side. .
Change the constants to equivalent fractions with the LCD. .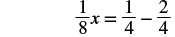
Subtract. .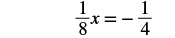
Multiply both sides by the reciprocal of \frac{1}{8}. .
Simplify. .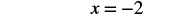

This method worked fine, but many students don’t feel very confident when they see all those fractions. So we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.

We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but with no fractions. This process is called clearing the equation of fractions. Let’s solve the same equation again, but this time use the method that clears the fractions.

EXAMPLE 1

Solve: \frac{1}{8}\phantom{\rule{0.1em}{0ex}}x+\frac{1}{2}=\frac{1}{4}.

Solution

Find the least common denominator of all the fractions in the equation. .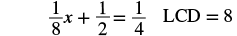
Multiply both sides of the equation by that LCD, 8. This clears the fractions. .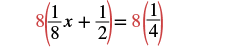
Use the Distributive Property. .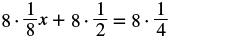
Simplify — and notice, no more fractions! .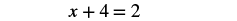
Solve using the General Strategy for Solving Linear Equations. .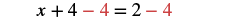
Simplify. .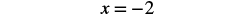
Check: Let x=-2 .

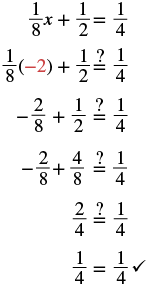TRY IT 1.1

Solve: \frac{1}{4}\phantom{\rule{0.1em}{0ex}}x+\frac{1}{2}=\frac{5}{8}.

Show answer

x=\frac{1}{2}

TRY IT 1.2

Solve: \frac{1}{6}\phantom{\rule{0.1em}{0ex}}y-\frac{1}{3}=\frac{1}{6}.

Show answer

y = 3

Notice in (Figure) that once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve! We then used the General Strategy for Solving Linear Equations.

HOW TO: Solve Equations with Fraction Coefficients by Clearing the Fractions

  1. Find the least common denominator of all the fractions in the equation.
  2. Multiply both sides of the equation by that LCD. This clears the fractions.
  3. Solve using the General Strategy for Solving Linear Equations.

EXAMPLE 2

Solve: 7=\frac{1}{2}\phantom{\rule{0.1em}{0ex}}x+\frac{3}{4}\phantom{\rule{0.1em}{0ex}}x-\frac{2}{3}\phantom{\rule{0.1em}{0ex}}x.

Solution

We want to clear the fractions by multiplying both sides of the equation by the LCD of all the fractions in the equation.

Find the least common denominator of all the fractions in the equation. .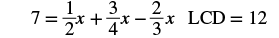
Multiply both sides of the equation by 12. .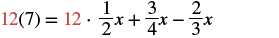
Distribute. .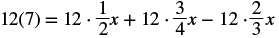
Simplify — and notice, no more fractions! .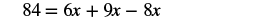
Combine like terms. .
Divide by 7. .
Simplify. .
Check: Let x=12. .

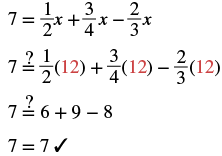TRY IT 2.1

Solve: 6=\frac{1}{2}\phantom{\rule{0.1em}{0ex}}v+\frac{2}{5}\phantom{\rule{0.1em}{0ex}}v-\frac{3}{4}\phantom{\rule{0.1em}{0ex}}v.

Show answer

v = 40

TRY IT 2.2

Solve: -1=\frac{1}{2}\phantom{\rule{0.1em}{0ex}}u+\frac{1}{4}\phantom{\rule{0.1em}{0ex}}u-\frac{2}{3}\phantom{\rule{0.1em}{0ex}}u.

Show answer

u = −12

In the next example, we’ll have variables and fractions on both sides of the equation.

EXAMPLE 3

Solve: x+\frac{1}{3}=\frac{1}{6}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{2}.

Solution

Find the LCD of all the fractions in the equation. .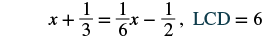
Multiply both sides by the LCD. .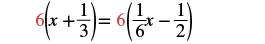
Distribute. .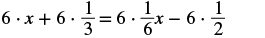
Simplify — no more fractions! .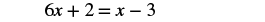
Subtract x from both sides. .
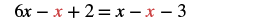Simplify. .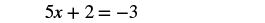
Subtract 2 from both sides. .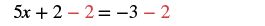
Simplify. .
Divide by 5. .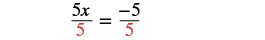
Simplify. .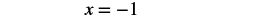
Check: Substitute x=-1. .

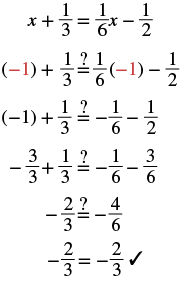TRY IT 3.1

Solve: a+\frac{3}{4}=\frac{3}{8}\phantom{\rule{0.1em}{0ex}}a-\frac{1}{2}.

Show answer

a = −2

TRY IT 3.2

Solve: c+\frac{3}{4}=\frac{1}{2}\phantom{\rule{0.1em}{0ex}}c-\frac{1}{4}.

Show answer

c = −2

In (Figure), we’ll start by using the Distributive Property. This step will clear the fractions right away!

EXAMPLE 4

Solve: 1=\frac{1}{2}\left(4x+2\right).

Solution

.
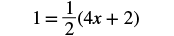Distribute. .
Simplify. Now there are no fractions to clear! .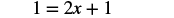
Subtract 1 from both sides. .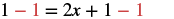
Simplify. .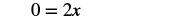
Divide by 2. .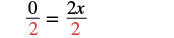
Simplify. .
Check: Let x=0. .

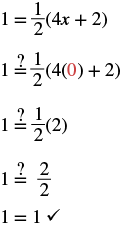TRY IT 4.1

Solve: -11=\frac{1}{2}\left(6p+2\right).

Show answer

p = −4

TRY IT 4.2

Solve: 8=\frac{1}{3}\left(9q+6\right).

Show answer

q = 2

Many times, there will still be fractions, even after distributing.

EXAMPLE 5

Solve: \frac{1}{2}\left(y-5\right)=\frac{1}{4}\left(y-1\right).

Solution

.
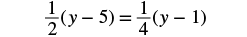Distribute. .
Simplify. .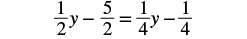
Multiply by the LCD, 4. .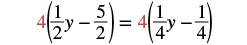
Distribute. .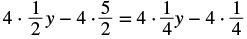
Simplify. .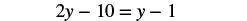
Collect the y terms to the left. .
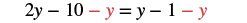Simplify. .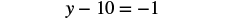
Collect the constants to the right. .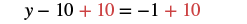
Simplify. .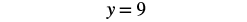
Check: Substitute 9 for y. .

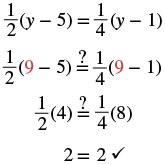TRY IT 5.1

Solve: \frac{1}{5}\left(n+3\right)=\frac{1}{4}\left(n+2\right).

Show answer

n = 2

TRY IT 5.2

Solve: \frac{1}{2}\left(m-3\right)=\frac{1}{4}\left(m-7\right).

Show answer

m = −1

Solve Equations with Decimal Coefficients

Some equations have decimals in them. This kind of equation will occur when we solve problems dealing with money and percent. But decimals are really another way to represent fractions. For example, 0.3=\frac{3}{10} and 0.17=\frac{17}{100}. So, when we have an equation with decimals, we can use the same process we used to clear fractions—multiply both sides of the equation by the least common denominator.

EXAMPLE 6

Solve: 0.8x-5=7.

Solution

The only decimal in the equation is 0.8. Since 0.8=\frac{8}{10}, the LCD is 10. We can multiply both sides by 10 to clear the decimal.

.
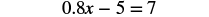Multiply both sides by the LCD. .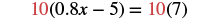
Distribute. .
Multiply, and notice, no more decimals! .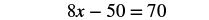
Add 50 to get all constants to the right. .
Simplify. .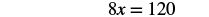
Divide both sides by 8. .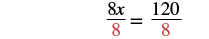
Simplify. .
Check: Let x=15. .

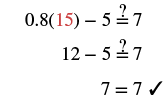TRY IT 6.1

Solve: 0.6x-1=11.

Show answer

x = 20

TRY IT 6.2

Solve: 1.2x-3=9.

Show answer

x = 10

EXAMPLE 7

Solve: 0.06x+0.02=0.25x-1.5.

Solution

Look at the decimals and think of the equivalent fractions.

0.06=\frac{6}{100},\phantom{\rule{1em}{0ex}}0.02=\frac{2}{100},\phantom{\rule{1em}{0ex}}0.25=\frac{25}{100},\phantom{\rule{1em}{0ex}}1.5=1\frac{5}{10}

Notice, the LCD is 100.

By multiplying by the LCD we will clear the decimals.

.
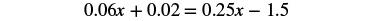Multiply both sides by 100. .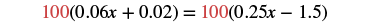
Distribute. .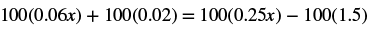
Multiply, and now no more decimals. .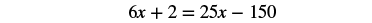
Collect the variables to the right. .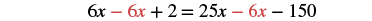
Simplify. .
Collect the constants to the left. .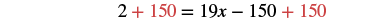
Simplify. .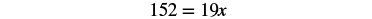
Divide by 19. .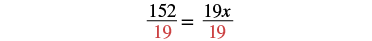
Simplify. .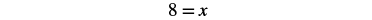
Check: Let x=8.
.

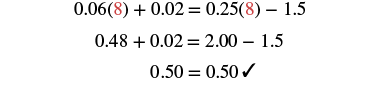TRY IT 7.1

Solve: 0.14h+0.12=0.35h-2.4.

Show answer

h = 12

TRY IT 7.2

Solve: 0.65k-0.1=0.4k-0.35.

Show answer

k = −1

The next example uses an equation that is typical of the ones we will see in the money applications in the next chapter. Notice that we will distribute the decimal first before we clear all decimals in the equation.

EXAMPLE 8

Solve: 0.25x+0.05\left(x+3\right)=2.85.

Solution

.
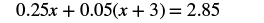Distribute first. .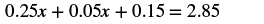
Combine like terms. .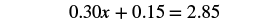
To clear decimals, multiply by 100. .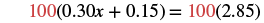
Distribute. .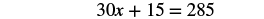
Subtract 15 from both sides. .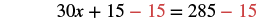
Simplify. .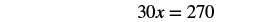
Divide by 30. .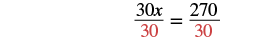
Simplify. .
Check: Let x=9. .

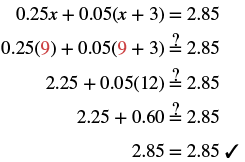TRY IT 8.1

Solve: 0.25n+0.05\left(n+5\right)=2.95.

Show answer

n = 9

TRY IT 8.2

Solve: 0.10d+0.05\left(d-5\right)=2.15.

Show answer

d = 16

Key Concepts

  • Solve equations with fraction coefficients by clearing the fractions.
    1. Find the least common denominator of all the fractions in the equation.
    2. Multiply both sides of the equation by that LCD. This clears the fractions.
    3. Solve using the General Strategy for Solving Linear Equations.

Practices Makes Perfect

Solve equations with fraction coefficients

In the following exercises, solve the equation by clearing the fractions.

1. \frac{1}{4}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{2}=-\frac{3}{4} 2. \frac{3}{4}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{2}=\frac{1}{4}
3. \frac{5}{6}\phantom{\rule{0.1em}{0ex}}y-\frac{2}{3}=-\frac{3}{2} 4. \frac{5}{6}\phantom{\rule{0.1em}{0ex}}y-\frac{1}{3}=-\frac{7}{6}
5. \frac{1}{2}\phantom{\rule{0.1em}{0ex}}a+\frac{3}{8}=\frac{3}{4} 6. \frac{5}{8}\phantom{\rule{0.1em}{0ex}}b+\frac{1}{2}=-\frac{3}{4}
7. 2=\frac{1}{3}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{2}\phantom{\rule{0.1em}{0ex}}x+\frac{2}{3}\phantom{\rule{0.1em}{0ex}}x 8. 2=\frac{3}{5}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{3}\phantom{\rule{0.1em}{0ex}}x+\frac{2}{5}\phantom{\rule{0.1em}{0ex}}x
9. \frac{1}{4}\phantom{\rule{0.1em}{0ex}}m-\frac{4}{5}\phantom{\rule{0.1em}{0ex}}m+\frac{1}{2}\phantom{\rule{0.1em}{0ex}}m=-1 10. \frac{5}{6}\phantom{\rule{0.1em}{0ex}}n-\frac{1}{4}\phantom{\rule{0.1em}{0ex}}n-\frac{1}{2}\phantom{\rule{0.1em}{0ex}}n=-2
11. x+\frac{1}{2}=\frac{2}{3}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{2} 12. x+\frac{3}{4}=\frac{1}{2}\phantom{\rule{0.1em}{0ex}}x-\frac{5}{4}
13. \frac{1}{3}\phantom{\rule{0.1em}{0ex}}w+\frac{5}{4}=w-\frac{1}{4} 14. \frac{3}{2}\phantom{\rule{0.1em}{0ex}}z+\frac{1}{3}=z-\frac{2}{3}
15. \frac{1}{2}\phantom{\rule{0.1em}{0ex}}x-\frac{1}{4}=\frac{1}{12}\phantom{\rule{0.1em}{0ex}}x+\frac{1}{6} 16. \frac{1}{2}\phantom{\rule{0.1em}{0ex}}a-\frac{1}{4}=\frac{1}{6}\phantom{\rule{0.1em}{0ex}}a+\frac{1}{12}
17. \frac{1}{3}\phantom{\rule{0.1em}{0ex}}b+\frac{1}{5}=\frac{2}{5}\phantom{\rule{0.1em}{0ex}}b-\frac{3}{5} 18. \frac{1}{3}\phantom{\rule{0.1em}{0ex}}x+\frac{2}{5}=\frac{1}{5}\phantom{\rule{0.1em}{0ex}}x-\frac{2}{5}
19. 1=\frac{1}{6}\left(12x-6\right) 20. 1=\frac{1}{5}\left(15x-10\right)
21. \frac{1}{4}\left(p-7\right)=\frac{1}{3}\left(p+5\right) 22. \frac{1}{5}\left(q+3\right)=\frac{1}{2}\left(q-3\right)
23. \frac{1}{2}\left(x+4\right)=\frac{3}{4} 24. \frac{1}{3}\left(x+5\right)=\frac{5}{6}

Solve Equations with Decimal Coefficients

In the following exercises, solve the equation by clearing the decimals.

25. 0.6y+3=9 26. 0.4y-4=2
27. 3.6j-2=5.2 28. 2.1k+3=7.2
29. 0.4x+0.6=0.5x-1.2 30. 0.7x+0.4=0.6x+2.4
31. 0.23x+1.47=0.37x-1.05 32. 0.48x+1.56=0.58x-0.64
33. 0.9x-1.25=0.75x+1.75 34. 1.2x-0.91=0.8x+2.29
35. 0.05n+0.10\left(n+8\right)=2.15 36. 0.05n+0.10\left(n+7\right)=3.55
37. 0.10d+0.25\left(d+5\right)=4.05 38. 0.10d+0.25\left(d+7\right)=5.25
39. 0.05\left(q-5\right)+0.25q=3.05 40. 0.05\left(q-8\right)+0.25q=4.10

Everyday Math

Coins  41. Taylor has \text{\$2.00} in dimes and pennies. The number of pennies is 2 more than the number of dimes. Solve the equation 0.10d+0.01\left(d+2\right)=2 for d, the number of dimes. Stamps 42.  Travis bought \text{\$9.45} worth of \text{49-cent} stamps and \text{21-cent} stamps. The number of \text{21-cent} stamps was 5 less than the number of \text{49-cent} stamps. Solve the equation 0.49s+0.21\left(s-5\right)=9.45 for s, to find the number of \text{49-cent} stamps Travis bought.

Writing Exercises

43. Explain how to find the least common denominator of \frac{3}{8},\phantom{\rule{0.2em}{0ex}}\frac{1}{6},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\frac{2}{3}. 44. If an equation has several fractions, how does multiplying both sides by the LCD make it easier to solve?
45. If an equation has fractions only on one side, why do you have to multiply both sides of the equation by the LCD? 46. In the equation 0.35x+2.1=3.85, what is the LCD? How do you know?

Answers

1. x = -1 3. y = -1 5. a=\frac{3}{4}
7. x = 4 9. m = 20 11. x = -3
13. w=\frac{9}{4} 15. x = 1 17. b = 12
19. x = 1 21. p = -41 23. x=-\frac{5}{2}
25. y = 10 27. j = 2 29. x = 18
31. x = 18 33. x = 20 35. n = 9
37. d = 8 39. q = 11 41 d = 18
43. Answers will vary. 45.Answers will vary.

Attributions

This chapter has been adapted from “Solve Equations with Fraction or Decimal Coefficients” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book