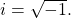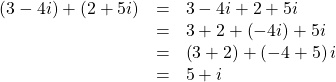Chapter 10.1: Complex Numbers
Learning Objectives
In this section you will:
- Add and subtract complex numbers.
- Multiply and divide complex numbers.
- Simplify powers of
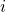 .
.

Discovered by Benoit Mandelbrot around 1980, the Mandelbrot Set is one of the most recognizable fractal images. The image is built on the theory of self-similarity and the operation of iteration. Zooming in on a fractal image brings many surprises, particularly in the high level of repetition of detail that appears as magnification increases. The equation that generates this image turns out to be rather simple.
In order to better understand it, we need to become familiar with a new set of numbers. Keep in mind that the study of mathematics continuously builds upon itself. Negative integers, for example, fill a void left by the set of positive integers. The set of rational numbers, in turn, fills a void left by the set of integers. The set of real numbers fills a void left by the set of rational numbers. Not surprisingly, the set of real numbers has voids as well. In this section, we will explore a set of numbers that fills voids in the set of real numbers and find out how to work within it.
Expressing Square Roots of Negative Numbers as Multiples of 
We know how to find the square root of any positive real number. In a similar way, we can find the square root of any negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number ![]() is defined as the square root of
is defined as the square root of ![]()
So, using properties of radicals,
We can write the square root of any negative number as a multiple of ![]() Consider the square root of
Consider the square root of ![]()
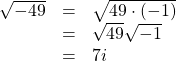
We use ![]() and not
and not ![]() because the principal root of
because the principal root of ![]() is the positive root.
is the positive root.
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written ![]() where
where ![]() is the real part and
is the real part and ![]() is the imaginary part. For example,
is the imaginary part. For example, ![]() is a complex number. So, too, is
is a complex number. So, too, is ![]()

Imaginary numbers differ from real numbers in that a squared imaginary number produces a negative real number. Recall that when a positive real number is squared, the result is a positive real number and when a negative real number is squared, the result is also a positive real number. Complex numbers consist of real and imaginary numbers.
Imaginary and Complex Numbers
A complex number is a number of the form ![]() where
where
 is the real part of the complex number.
is the real part of the complex number. is the imaginary part of the complex number.
is the imaginary part of the complex number.
If ![]() then
then ![]() is a real number. If
is a real number. If ![]() and
and ![]() is not equal to 0, the complex number is called a pure imaginary number. An imaginary number is an even root of a negative number.
is not equal to 0, the complex number is called a pure imaginary number. An imaginary number is an even root of a negative number.
How To
Given an imaginary number, express it in the standard form of a complex number.
- Write
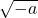 as
as 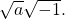
- Express
 as
as 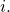
- Write
 in simplest form.
in simplest form.
Expressing an Imaginary Number in Standard Form
Express ![]() in standard form.
in standard form.
Show Solution
In standard form, this is ![]()
Try It
Express ![]() in standard form.
in standard form.
Show Solution
![]()
Plotting a Complex Number on the Complex Plane
We cannot plot complex numbers on a number line as we might real numbers. However, we can still represent them graphically. To represent a complex number, we need to address the two components of the number. We use the complex plane, which is a coordinate system in which the horizontal axis represents the real component and the vertical axis represents the imaginary component. Complex numbers are the points on the plane, expressed as ordered pairs ![]() where
where ![]() represents the coordinate for the horizontal axis and
represents the coordinate for the horizontal axis and ![]() represents the coordinate for the vertical axis.
represents the coordinate for the vertical axis.
Let’s consider the number ![]() The real part of the complex number is
The real part of the complex number is ![]() and the imaginary part is 3. We plot the ordered pair
and the imaginary part is 3. We plot the ordered pair ![]() to represent the complex number
to represent the complex number ![]() as shown in (Figure).
as shown in (Figure).

Complex Plane
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis, as shown in (Figure).

How To
Given a complex number, represent its components on the complex plane.
- Determine the real part and the imaginary part of the complex number.
- Move along the horizontal axis to show the real part of the number.
- Move parallel to the vertical axis to show the imaginary part of the number.
- Plot the point.
Plotting a Complex Number on the Complex Plane
Plot the complex number ![]() on the complex plane.
on the complex plane.
Show Solution
The real part of the complex number is ![]() and the imaginary part is –4. We plot the ordered pair
and the imaginary part is –4. We plot the ordered pair ![]() as shown in (Figure).
as shown in (Figure).

Try It
Plot the complex number ![]() on the complex plane.
on the complex plane.
Show Solution

Adding and Subtracting Complex Numbers
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and then combine the imaginary parts.
Complex Numbers: Addition and Subtraction
Adding complex numbers:
Subtracting complex numbers:
How To
Given two complex numbers, find the sum or difference.
- Identify the real and imaginary parts of each number.
- Add or subtract the real parts.
- Add or subtract the imaginary parts.
Adding and Subtracting Complex Numbers
Add or subtract as indicated.
Show Solution
We add the real parts and add the imaginary parts.
Try It
Subtract ![]() from
from ![]()
Show Solution
![]()
Multiplying Complex Numbers
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Multiplying a Complex Number by a Real Number
Lets begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. Consider, for example, ![]() :
:

How To
Given a complex number and a real number, multiply to find the product.
- Use the distributive property.
- Simplify.
Multiplying a Complex Number by a Real Number
Find the product ![]()
Show Solution
Distribute the 4.
Try It
Find the product: ![]()
Show Solution
![]()
Multiplying Complex Numbers Together
Now, let’s multiply two complex numbers. We can use either the distributive property or more specifically the FOIL method because we are dealing with binomials. Recall that FOIL is an acronym for multiplying First, Inner, Outer, and Last terms together. The difference with complex numbers is that when we get a squared term, ![]() it equals
it equals ![]()
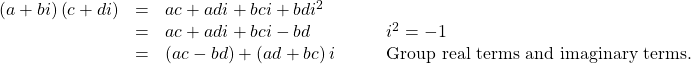
How To
Given two complex numbers, multiply to find the product.
- Use the distributive property or the FOIL method.
- Remember that

- Group together the real terms and the imaginary terms
Multiplying a Complex Number by a Complex Number
Multiply: ![]()
Show Solution
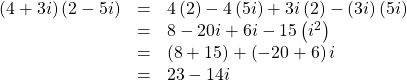
Try It
Multiply: ![]()
Show Solution
![]()
Dividing Complex Numbers
Dividing two complex numbers is more complicated than adding, subtracting, or multiplying because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator to write the answer in standard form ![]() We need to find a term by which we can multiply the numerator and the denominator that will eliminate the imaginary portion of the denominator so that we end up with a real number as the denominator. This term is called the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. In other words, the complex conjugate of
We need to find a term by which we can multiply the numerator and the denominator that will eliminate the imaginary portion of the denominator so that we end up with a real number as the denominator. This term is called the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. In other words, the complex conjugate of ![]() is
is ![]() For example, the product of
For example, the product of ![]() and
and ![]() is
is
The result is a real number.
Note that complex conjugates have an opposite relationship: The complex conjugate of ![]() is
is ![]() and the complex conjugate of
and the complex conjugate of ![]() is
is ![]() Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another.
Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another.
Suppose we want to divide ![]() by
by ![]() where neither
where neither ![]() nor
nor ![]() equals zero. We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.
equals zero. We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.
Multiply the numerator and denominator by the complex conjugate of the denominator.
Apply the distributive property.
Simplify, remembering that ![]()
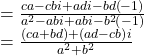
The Complex Conjugate
The complex conjugate of a complex number ![]() is
is ![]() It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.
It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.
- When a complex number is multiplied by its complex conjugate, the result is a real number.
- When a complex number is added to its complex conjugate, the result is a real number.
Finding Complex Conjugates
Find the complex conjugate of each number.
Show Solution
- The number is already in the form
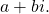 The complex conjugate is
The complex conjugate is 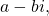 or
or 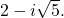
- We can rewrite this number in the form
 as
as 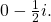 The complex conjugate is
The complex conjugate is 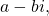 or
or  This can be written simply as
This can be written simply as 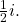
Analysis
Although we have seen that we can find the complex conjugate of an imaginary number, in practice we generally find the complex conjugates of only complex numbers with both a real and an imaginary component. To obtain a real number from an imaginary number, we can simply multiply by ![]()
Try It
Find the complex conjugate of ![]()
Show Solution
![]()
How To
Given two complex numbers, divide one by the other.
- Write the division problem as a fraction.
- Determine the complex conjugate of the denominator.
- Multiply the numerator and denominator of the fraction by the complex conjugate of the denominator.
- Simplify.
Dividing Complex Numbers
Divide: ![]() by
by ![]()
Show Solution
We begin by writing the problem as a fraction.
Then we multiply the numerator and denominator by the complex conjugate of the denominator.
To multiply two complex numbers, we expand the product as we would with polynomials (using FOIL).

Note that this expresses the quotient in standard form.
Simplifying Powers of i
The powers of ![]() are cyclic. Let’s look at what happens when we raise
are cyclic. Let’s look at what happens when we raise ![]() to increasing powers.
to increasing powers.
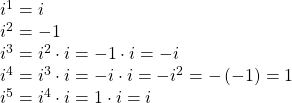
We can see that when we get to the fifth power of ![]() it is equal to the first power. As we continue to multiply
it is equal to the first power. As we continue to multiply ![]() by increasing powers, we will see a cycle of four. Let’s examine the next four powers of
by increasing powers, we will see a cycle of four. Let’s examine the next four powers of ![]()
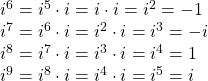
The cycle is repeated continuously: ![]() every four powers.
every four powers.
Simplifying Powers of 
Evaluate: ![]()
Show Solution
Since ![]() we can simplify the problem by factoring out as many factors of
we can simplify the problem by factoring out as many factors of ![]() as possible. To do so, first determine how many times 4 goes into 35:
as possible. To do so, first determine how many times 4 goes into 35: ![]()
Try It
Evaluate: ![]()
Show Solution
![]()
Can we write ![]() in other helpful ways?
in other helpful ways?
As we saw in (Figure), we reduced ![]() to
to ![]() by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of
by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of ![]() may be more useful. (Figure) shows some other possible factorizations.
may be more useful. (Figure) shows some other possible factorizations.
| Factorization of |
||||
| Reduced form | ||||
| Simplified form |
Each of these will eventually result in the answer we obtained above but may require several more steps than our earlier method.
Access these online resources for additional instruction and practice with complex numbers.
Key Concepts
- The square root of any negative number can be written as a multiple of
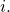 See (Figure).
See (Figure). - To plot a complex number, we use two number lines, crossed to form the complex plane. The horizontal axis is the real axis, and the vertical axis is the imaginary axis. See (Figure).
- Complex numbers can be added and subtracted by combining the real parts and combining the imaginary parts. See (Figure).
- Complex numbers can be multiplied and divided.
- The powers of
 are cyclic, repeating every fourth one. See (Figure).
are cyclic, repeating every fourth one. See (Figure).
Section Exercises
Verbal
1. Explain how to add complex numbers.
Show Solution
Add the real parts together and the imaginary parts together.
2. What is the basic principle in multiplication of complex numbers?
3. Give an example to show that the product of two imaginary numbers is not always imaginary.
Show Solution
Possible answer: ![]() times
times ![]() equals -1, which is not imaginary.
equals -1, which is not imaginary.
4. What is a characteristic of the plot of a real number in the complex plane?
Algebraic
For the following exercises, evaluate the algebraic expressions.
5. If ![]() evaluate
evaluate ![]() given
given ![]()
Show Solution
![]()
6. If ![]() evaluate
evaluate ![]() given
given ![]()
7. If ![]() evaluate
evaluate ![]() given
given ![]()
Show Solution
![]()
8. If ![]() evaluate
evaluate ![]() given
given ![]()
9. If ![]() evaluate
evaluate ![]() given
given ![]()
Show Solution
![]()
10. If ![]() evaluate
evaluate ![]() given
given ![]()
Graphical
For the following exercises, plot the complex numbers on the complex plane.
11. ![]()
Show Solution

12. ![]()
13. ![]()
Show Solution

14. ![]()
Numeric
For the following exercises, perform the indicated operation and express the result as a simplified complex number.
15. ![]()
Show Solution
![]()
16. ![]()
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
![]()
26. ![]()
27. ![]()
Show Solution
25
28. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
35. ![]()
Show Solution
![]()
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
41. ![]()
Show Solution
![]()
Technology
For the following exercises, use a calculator to help answer the questions.
42. Evaluate ![]() for
for ![]() Predict the value if
Predict the value if ![]()
43. Evaluate ![]() for
for ![]() Predict the value if
Predict the value if ![]()
Show Solution
128i
44. Evaluate ![]() for
for ![]() Predict the value for
Predict the value for ![]()
45. Show that a solution of ![]() is
is ![]()
Show Solution
![]()
46. Show that a solution of ![]() is
is ![]()
Extensions
For the following exercises, evaluate the expressions, writing the result as a simplified complex number.
47. ![]()
Show Solution
![]()
48. ![]()
49. ![]()
Show Solution
0
50. ![]()
51. ![]()
Show Solution
![]()
52. ![]()
53. ![]()
Show Solution
![]()
54. ![]()
55. ![]()
Show Solution
![]()
56. ![]()
Glossary
- complex conjugate
- a complex number containing the same terms as another complex number, but with the opposite operator. Multiplying a complex number by its conjugate yields a real number.
- complex number
- the sum of a real number and an imaginary number; the standard form is
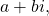 where a is the real part and
where a is the real part and 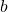 is the complex part.
is the complex part.
- complex plane
- the coordinate plane in which the horizontal axis represents the real component of a complex number, and the vertical axis represents the imaginary component, labeled i.
- imaginary number
- the square root of
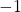 :
: