Chapter 9.4: Logarithmic Functions
Learning Objectives
In this section, you will:
- Convert from logarithmic to exponential form.
- Convert from exponential to logarithmic form.
- Evaluate logarithms.
- Use common logarithms.
- Use natural logarithms.

In 2010, a major earthquake struck Haiti, destroying or damaging over 285,000 homes[1] . One year later, another, stronger earthquake devastated Honshu, Japan, destroying or damaging over 332,000 buildings,[2] like those shown in (Figure). Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale[3] whereas the Japanese earthquake registered a 9.0.[4]
The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude 8 is not twice as great as an earthquake of magnitude 4. It is ![]() times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
Converting from Logarithmic to Exponential Form
In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake were 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is ![]() where
where ![]() represents the difference in magnitudes on the Richter Scale. How would we solve for
represents the difference in magnitudes on the Richter Scale. How would we solve for ![]()
We have not yet learned a method for solving exponential equations. None of the algebraic tools discussed so far is sufficient to solve ![]() We know that
We know that ![]() and
and ![]() so it is clear that
so it is clear that ![]() must be some value between 2 and 3, since
must be some value between 2 and 3, since ![]() is increasing. We can examine a graph, as in (Figure), to better estimate the solution.
is increasing. We can examine a graph, as in (Figure), to better estimate the solution.

Estimating from a graph, however, is imprecise. To find an algebraic solution, we must introduce a new function. Observe that the graph in (Figure) passes the horizontal line test. The exponential function ![]() is one-to-one, so its inverse,
is one-to-one, so its inverse, ![]() is also a function. As is the case with all inverse functions, we simply interchange
is also a function. As is the case with all inverse functions, we simply interchange ![]() and
and ![]() and solve for
and solve for ![]() to find the inverse function. To represent
to find the inverse function. To represent ![]() as a function of
as a function of ![]() we use a logarithmic function of the form
we use a logarithmic function of the form ![]() The base
The base ![]() logarithm of a number is the exponent by which we must raise
logarithm of a number is the exponent by which we must raise ![]() to get that number.
to get that number.
We read a logarithmic expression as, “The logarithm with base ![]() of
of ![]() is equal to
is equal to ![]() ” or, simplified, “log base
” or, simplified, “log base ![]() of
of ![]() is
is ![]() ” We can also say, “
” We can also say, “ ![]() raised to the power of
raised to the power of ![]() is
is ![]() ” because logs are exponents. For example, the base 2 logarithm of 32 is 5, because 5 is the exponent we must apply to 2 to get 32. Since
” because logs are exponents. For example, the base 2 logarithm of 32 is 5, because 5 is the exponent we must apply to 2 to get 32. Since ![]() we can write
we can write ![]() We read this as “log base 2 of 32 is 5.”
We read this as “log base 2 of 32 is 5.”
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
Note that the base ![]() is always positive.
is always positive.

Because logarithm is a function, it is most correctly written as ![]() using parentheses to denote function evaluation, just as we would with
using parentheses to denote function evaluation, just as we would with ![]() However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as
However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as ![]() Note that many calculators require parentheses around the
Note that many calculators require parentheses around the ![]()
We can illustrate the notation of logarithms as follows:

Notice that, comparing the logarithm function and the exponential function, the input and the output are switched. This means ![]() and
and ![]() are inverse functions.
are inverse functions.
Definition of the Logarithmic Function
A logarithm base ![]() of a positive number
of a positive number ![]() satisfies the following definition.
satisfies the following definition.
For ![]()
where,
- we read
 as, “the logarithm with base
as, “the logarithm with base 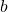 of
of 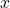 ” or the “log base
” or the “log base 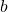 of
of 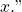
- the logarithm
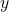 is the exponent to which
is the exponent to which 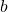 must be raised to get
must be raised to get 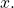
Also, since the logarithmic and exponential functions switch the ![]() and
and ![]() values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
- the domain of the logarithm function with base
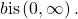
- the range of the logarithm function with base
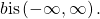
Can we take the logarithm of a negative number?
No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.
How To
Given an equation in logarithmic form ![]() convert it to exponential form.
convert it to exponential form.
- Examine the equation
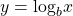 and identify
and identify 
- Rewrite
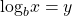 as
as 
Converting from Logarithmic Form to Exponential Form
Write the following logarithmic equations in exponential form.
Show Solution
First, identify the values of ![]() Then, write the equation in the form
Then, write the equation in the form ![]()
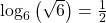
Here,
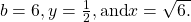 Therefore, the equation
Therefore, the equation  is equivalent to
is equivalent to 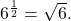
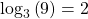
Here,
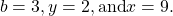 Therefore, the equation
Therefore, the equation 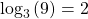 is equivalent to
is equivalent to 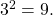
Try It
Write the following logarithmic equations in exponential form.
Show Solution
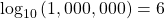 is equivalent to
is equivalent to 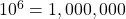
 is equivalent to
is equivalent to 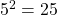
Converting from Exponential to Logarithmic Form
To convert from exponents to logarithms, we follow the same steps in reverse. We identify the base ![]() exponent
exponent ![]() and output
and output ![]() Then we write
Then we write ![]()
Converting from Exponential Form to Logarithmic Form
Write the following exponential equations in logarithmic form.
Show Solution
First, identify the values of ![]() Then, write the equation in the form
Then, write the equation in the form ![]()
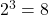
Here,
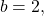
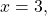 and
and 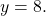 Therefore, the equation
Therefore, the equation 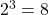 is equivalent to
is equivalent to 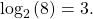
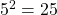
Here,
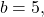
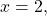 and
and 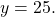 Therefore, the equation
Therefore, the equation  is equivalent to
is equivalent to 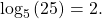
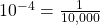
Here,
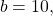
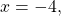 and
and 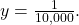 Therefore, the equation
Therefore, the equation 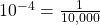 is equivalent to
is equivalent to 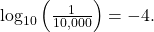
Try It
Write the following exponential equations in logarithmic form.
Show Solution
 is equivalent to
is equivalent to 
 is equivalent to
is equivalent to 
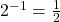 is equivalent to
is equivalent to 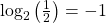
Evaluating Logarithms
Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. For example, consider ![]() We ask, “To what exponent must
We ask, “To what exponent must ![]() be raised in order to get 8?” Because we already know
be raised in order to get 8?” Because we already know ![]() it follows that
it follows that ![]()
Now consider solving ![]() and
and ![]() mentally.
mentally.
- We ask, “To what exponent must 7 be raised in order to get 49?” We know
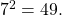 Therefore,
Therefore, 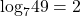
- We ask, “To what exponent must 3 be raised in order to get 27?” We know
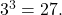 Therefore,
Therefore, 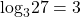
Even some seemingly more complicated logarithms can be evaluated without a calculator. For example, let’s evaluate ![]() mentally.
mentally.
- We ask, “To what exponent must
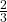 be raised in order to get
be raised in order to get 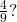 ” We know
” We know 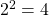 and
and  so
so  Therefore,
Therefore, 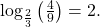
How To
Given a logarithm of the form ![]() evaluate it mentally.
evaluate it mentally.
- Rewrite the argument
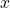 as a power of
as a power of 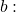
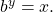
- Use previous knowledge of powers of
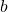 identify
identify 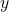 by asking, “To what exponent should
by asking, “To what exponent should 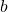 be raised in order to get
be raised in order to get 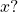 ”
”
Solving Logarithms Mentally
Solve ![]() without using a calculator.
without using a calculator.
Show Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must 4 be raised in order to get 64?”
Next, we ask, “To what exponent must 4 be raised in order to get 64?”
We know
Therefore,
Try It
Solve ![]() without using a calculator.
without using a calculator.
Show Solution
![]() (recalling that
(recalling that ![]() )
)
Evaluating the Logarithm of a Reciprocal
Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must 3 be raised in order to get
Next, we ask, “To what exponent must 3 be raised in order to get ![]() ”
”
We know ![]() but what must we do to get the reciprocal,
but what must we do to get the reciprocal, ![]() Recall from working with exponents that
Recall from working with exponents that ![]() We use this information to write
We use this information to write
Therefore, ![]()
Try It
Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
![]()
Using Common Logarithms
Sometimes we may see a logarithm written without a base. In this case, we assume that the base is 10. In other words, the expression ![]() means
means ![]() We call a base-10 logarithm a common logarithm. Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section. Scales for measuring the brightness of stars and the pH of acids and bases also use common logarithms.
We call a base-10 logarithm a common logarithm. Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section. Scales for measuring the brightness of stars and the pH of acids and bases also use common logarithms.
Definition of the Common Logarithm
A common logarithm is a logarithm with base ![]() We write
We write ![]() simply as
simply as ![]() The common logarithm of a positive number
The common logarithm of a positive number ![]() satisfies the following definition.
satisfies the following definition.
For ![]()
We read ![]() as, “the logarithm with base
as, “the logarithm with base ![]() of
of ![]() ” or “log base 10 of
” or “log base 10 of ![]() ”
”
The logarithm ![]() is the exponent to which
is the exponent to which ![]() must be raised to get
must be raised to get ![]()
How To
Given a common logarithm of the form ![]() evaluate it mentally.
evaluate it mentally.
- Rewrite the argument
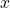 as a power of
as a power of 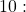
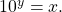
- Use previous knowledge of powers of
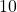 to identify
to identify 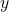 by asking, “To what exponent must
by asking, “To what exponent must 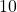 be raised in order to get
be raised in order to get 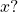 ”
”
Finding the Value of a Common Logarithm Mentally
Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must
Next, we ask, “To what exponent must ![]() be raised in order to get 1000?” We know
be raised in order to get 1000?” We know
Therefore, ![]()
Try It
Evaluate ![]()
Show Solution
![]()
How To
Given a common logarithm with the form ![]() evaluate it using a calculator.
evaluate it using a calculator.
- Press [LOG].
- Enter the value given for
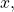 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Finding the Value of a Common Logarithm Using a Calculator
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Show Solution
- Press [LOG].
- Enter 321, followed by [ ) ].
- Press [ENTER].
Rounding to four decimal places, ![]()
Analysis
Note that ![]() and that
and that ![]() Since 321 is between 100 and 1000, we know that
Since 321 is between 100 and 1000, we know that ![]() must be between
must be between ![]() and
and ![]() This gives us the following:
This gives us the following:
Try It
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Show Solution
![]()
Rewriting and Solving a Real-World Exponential Model
The amount of energy released from one earthquake was 500 times greater than the amount of energy released from another. The equation ![]() represents this situation, where
represents this situation, where ![]() is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
Show Solution
We begin by rewriting the exponential equation in logarithmic form.
Next we evaluate the logarithm using a calculator:
- Press [LOG].
- Enter
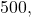 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
- To the nearest thousandth,
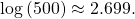
The difference in magnitudes was about ![]()
Try It
The amount of energy released from one earthquake was ![]() times greater than the amount of energy released from another. The equation
times greater than the amount of energy released from another. The equation ![]() represents this situation, where
represents this situation, where ![]() is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
Show Solution
The difference in magnitudes was about ![]()
Using Natural Logarithms
The most frequently used base for logarithms is ![]() Base
Base ![]() logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base
logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base ![]() logarithm,
logarithm, ![]() has its own notation,
has its own notation, ![]()
Most values of ![]() can be found only using a calculator. The major exception is that, because the logarithm of 1 is always 0 in any base,
can be found only using a calculator. The major exception is that, because the logarithm of 1 is always 0 in any base, ![]() For other natural logarithms, we can use the
For other natural logarithms, we can use the ![]() key that can be found on most scientific calculators. We can also find the natural logarithm of any power of
key that can be found on most scientific calculators. We can also find the natural logarithm of any power of ![]() using the inverse property of logarithms.
using the inverse property of logarithms.
Definition of the Natural Logarithm
A natural logarithm is a logarithm with base ![]() We write
We write ![]() simply as
simply as ![]() The natural logarithm of a positive number
The natural logarithm of a positive number ![]() satisfies the following definition.
satisfies the following definition.
For ![]()
We read ![]() as, “the logarithm with base
as, “the logarithm with base ![]() of
of ![]() ” or “the natural logarithm of
” or “the natural logarithm of ![]() ”
”
The logarithm ![]() is the exponent to which
is the exponent to which ![]() must be raised to get
must be raised to get ![]()
Since the functions ![]() and
and ![]() are inverse functions,
are inverse functions, ![]() for all
for all ![]() and
and ![]() for
for ![]()
How To
Given a natural logarithm with the form ![]() evaluate it using a calculator.
evaluate it using a calculator.
- Press [LN].
- Enter the value given for
 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Evaluating a Natural Logarithm Using a Calculator
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Show Solution
- Press [LN].
- Enter
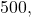 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Rounding to four decimal places, ![]()
Try It
Evaluate ![]()
Show Solution
It is not possible to take the logarithm of a negative number in the set of real numbers.
Access this online resource for additional instruction and practice with logarithms.
Key Equations
| Definition of the logarithmic function | For |
| Definition of the common logarithm | For |
| Definition of the natural logarithm | For |
Key Concepts
- The inverse of an exponential function is a logarithmic function, and the inverse of a logarithmic function is an exponential function.
- Logarithmic equations can be written in an equivalent exponential form, using the definition of a logarithm. See (Figure).
- Exponential equations can be written in their equivalent logarithmic form using the definition of a logarithm See (Figure).
- Logarithmic functions with base
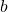 can be evaluated mentally using previous knowledge of powers of
can be evaluated mentally using previous knowledge of powers of 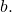 See (Figure) and (Figure).
See (Figure) and (Figure). - Common logarithms can be evaluated mentally using previous knowledge of powers of
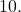 See (Figure).
See (Figure). - When common logarithms cannot be evaluated mentally, a calculator can be used. See (Figure).
- Real-world exponential problems with base
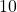 can be rewritten as a common logarithm and then evaluated using a calculator. See (Figure).
can be rewritten as a common logarithm and then evaluated using a calculator. See (Figure). - Natural logarithms can be evaluated using a calculator (Figure).
Section Exercises
Verbal
1. What is a base ![]() logarithm? Discuss the meaning by interpreting each part of the equivalent equations
logarithm? Discuss the meaning by interpreting each part of the equivalent equations ![]() and
and ![]() for
for ![]()
Show Solution
A logarithm is an exponent. Specifically, it is the exponent to which a base ![]() is raised to produce a given value. In the expressions given, the base
is raised to produce a given value. In the expressions given, the base ![]() has the same value. The exponent,
has the same value. The exponent, ![]() in the expression
in the expression ![]() can also be written as the logarithm,
can also be written as the logarithm, ![]() and the value of
and the value of ![]() is the result of raising
is the result of raising ![]() to the power of
to the power of ![]()
2. How is the logarithmic function ![]() related to the exponential function
related to the exponential function ![]() What is the result of composing these two functions?
What is the result of composing these two functions?
3. How can the logarithmic equation ![]() be solved for
be solved for ![]() using the properties of exponents?
using the properties of exponents?
Show Solution
Since the equation of a logarithm is equivalent to an exponential equation, the logarithm can be converted to the exponential equation ![]() and then properties of exponents can be applied to solve for
and then properties of exponents can be applied to solve for ![]()
4. Discuss the meaning of the common logarithm. What is its relationship to a logarithm with base ![]() and how does the notation differ?
and how does the notation differ?
5. Discuss the meaning of the natural logarithm. What is its relationship to a logarithm with base ![]() and how does the notation differ?
and how does the notation differ?
Show Solution
The natural logarithm is a special case of the logarithm with base ![]() in that the natural log always has base
in that the natural log always has base ![]() Rather than notating the natural logarithm as
Rather than notating the natural logarithm as ![]() the notation used is
the notation used is ![]()
Algebraic
For the following exercises, rewrite each equation in exponential form.
6. ![]()
7. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
![]()
14. ![]()
15. ![]()
Show Solution
![]()
For the following exercises, rewrite each equation in logarithmic form.
16. ![]()
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
![]()
For the following exercises, solve for ![]() by converting the logarithmic equation to exponential form.
by converting the logarithmic equation to exponential form.
26. ![]()
27. ![]()
Show Solution
![]()
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
35. ![]()
Show Solution
![]()
For the following exercises, use the definition of common and natural logarithms to simplify.
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
41. ![]()
Show Solution
![]()
Numeric
For the following exercises, evaluate the base ![]() logarithmic expression without using a calculator.
logarithmic expression without using a calculator.
42. ![]()
43. ![]()
Show Solution
![]()
44. ![]()
45. ![]()
Show Solution
![]()
For the following exercises, evaluate the common logarithmic expression without using a calculator.
46. ![]()
47. ![]()
Show Solution
![]()
48. ![]()
49. ![]()
Show Solution
![]()
For the following exercises, evaluate the natural logarithmic expression without using a calculator.
50. ![]()
51. ![]()
Show Solution
![]()
52. ![]()
53. ![]()
Show Solution
![]()
Technology
For the following exercises, evaluate each expression using a calculator. Round to the nearest thousandth.
54. ![]()
55. ![]()
Show Solution
![]()
56. ![]()
57. ![]()
Show Solution
![]()
58. ![]()
Extensions
59. Is ![]() in the domain of the function
in the domain of the function ![]() If so, what is the value of the function when
If so, what is the value of the function when ![]() Verify the result.
Verify the result.
Show Solution
No, the function has no defined value for ![]() To verify, suppose
To verify, suppose ![]() is in the domain of the function
is in the domain of the function ![]() Then there is some number
Then there is some number ![]() such that
such that ![]() Rewriting as an exponential equation gives:
Rewriting as an exponential equation gives: ![]() which is impossible since no such real number
which is impossible since no such real number ![]() exists. Therefore,
exists. Therefore, ![]() is not the domain of the function
is not the domain of the function ![]()
60. Is ![]() in the range of the function
in the range of the function ![]() If so, for what value of
If so, for what value of ![]() Verify the result.
Verify the result.
61. Is there a number ![]() such that
such that ![]() If so, what is that number? Verify the result.
If so, what is that number? Verify the result.
Show Solution
Yes. Suppose there exists a real number ![]() such that
such that ![]() Rewriting as an exponential equation gives
Rewriting as an exponential equation gives ![]() which is a real number. To verify, let
which is a real number. To verify, let ![]() Then, by definition,
Then, by definition, ![]()
62. Is the following true: ![]() Verify the result.
Verify the result.
63. Is the following true: ![]() Verify the result.
Verify the result.
Show Solution
No; ![]() so
so ![]() is undefined.
is undefined.
Real-World Applications
64. The exposure index ![]() for a 35 millimeter camera is a measurement of the amount of light that hits the film. It is determined by the equation
for a 35 millimeter camera is a measurement of the amount of light that hits the film. It is determined by the equation ![]() where
where ![]() is the “f-stop” setting on the camera, and
is the “f-stop” setting on the camera, and ![]() is the exposure time in seconds. Suppose the f-stop setting is
is the exposure time in seconds. Suppose the f-stop setting is ![]() and the desired exposure time is
and the desired exposure time is ![]() seconds. What will the resulting exposure index be?
seconds. What will the resulting exposure index be?
65. Refer to the previous exercise. Suppose the light meter on a camera indicates an ![]() of
of ![]() and the desired exposure time is 16 seconds. What should the f-stop setting be?
and the desired exposure time is 16 seconds. What should the f-stop setting be?
Show Solution
![]()
66. The intensity levels I of two earthquakes measured on a seismograph can be compared by the formula ![]() where
where ![]() is the magnitude given by the Richter Scale. In August 2009, an earthquake of magnitude 6.1 hit Honshu, Japan. In March 2011, that same region experienced yet another, more devastating earthquake, this time with a magnitude of 9.0.[5] How many times greater was the intensity of the 2011 earthquake? Round to the nearest whole number.
is the magnitude given by the Richter Scale. In August 2009, an earthquake of magnitude 6.1 hit Honshu, Japan. In March 2011, that same region experienced yet another, more devastating earthquake, this time with a magnitude of 9.0.[5] How many times greater was the intensity of the 2011 earthquake? Round to the nearest whole number.
Glossary
- common logarithm
- the exponent to which 10 must be raised to get
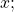
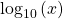 is written simply as
is written simply as 
- logarithm
- the exponent to which
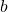 must be raised to get
must be raised to get 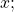 written
written 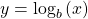
- natural logarithm
- the exponent to which the number
 must be raised to get
must be raised to get 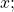
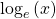 is written as
is written as 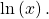
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/#summary. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#summary. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. Accessed 3/4/2013. ↵
- http://earthquake.usgs.gov/earthquakes/world/historical.php. Accessed 3/4/2014. ↵

