Chapter 6.9: Rational Functions
Learning Objectives
In this section, you will:
- Use arrow notation.
- Solve applied problems involving rational functions.
- Find the domains of rational functions.
- Identify vertical asymptotes.
- Identify horizontal asymptotes.
- Graph rational functions.
Suppose we know that the cost of making a product is dependent on the number of items, ![]() produced. This is given by the equation
produced. This is given by the equation ![]() If we want to know the average cost for producing
If we want to know the average cost for producing ![]() items, we would divide the cost function by the number of items,
items, we would divide the cost function by the number of items, ![]()
The average cost function, which yields the average cost per item for ![]() items produced, is
items produced, is
Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.
In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.
Using Arrow Notation
We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Examine these graphs, as shown in (Figure), and notice some of their features.

Several things are apparent if we examine the graph of ![]()
- On the left branch of the graph, the curve approaches the x-axis
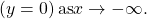
- As the graph approaches
 from the left, the curve drops, but as we approach zero from the right, the curve rises.
from the left, the curve drops, but as we approach zero from the right, the curve rises. - Finally, on the right branch of the graph, the curves approaches the x-axis
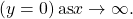
To summarize, we use arrow notation to show that ![]() or
or ![]() is approaching a particular value. See (Figure).
is approaching a particular value. See (Figure).
| Symbol | Meaning |
|---|---|
| the output approaches infinity (the output increases without bound) | |
| the output approaches negative infinity (the output decreases without bound) | |
| the output approaches |
Local Behavior of 
Let’s begin by looking at the reciprocal function, ![]() We cannot divide by zero, which means the function is undefined at
We cannot divide by zero, which means the function is undefined at ![]() so zero is not in the domain. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in (Figure).
so zero is not in the domain. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in (Figure).
| |
–0.1 | –0.01 | –0.001 | –0.0001 |
| |
–10 | –100 | –1000 | –10,000 |
We write in arrow notation
As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). We can see this behavior in (Figure).
| |
0.1 | 0.01 | 0.001 | 0.0001 |
| |
10 | 100 | 1000 | 10,000 |
We write in arrow notation
See (Figure).

This behavior creates a vertical asymptote, which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line ![]() as the input becomes close to zero. See (Figure).
as the input becomes close to zero. See (Figure).

Vertical Asymptote
A vertical asymptote of a graph is a vertical line ![]() where the graph tends toward positive or negative infinity as the inputs approach
where the graph tends toward positive or negative infinity as the inputs approach ![]() We write
We write
End Behavior of 
As the values of ![]() approach infinity, the function values approach 0. As the values of
approach infinity, the function values approach 0. As the values of ![]() approach negative infinity, the function values approach 0. See (Figure). Symbolically, using arrow notation
approach negative infinity, the function values approach 0. See (Figure). Symbolically, using arrow notation
![]()

Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. This behavior creates a horizontal asymptote, a horizontal line that the graph approaches as the input increases or decreases without bound. In this case, the graph is approaching the horizontal line ![]() See (Figure).
See (Figure).

Horizontal Asymptote
A horizontal asymptote of a graph is a horizontal line ![]() where the graph approaches the line as the inputs increase or decrease without bound. We write
where the graph approaches the line as the inputs increase or decrease without bound. We write
Using Arrow Notation
Use arrow notation to describe the end behavior and local behavior of the function graphed in (Figure).

Show Solution
Notice that the graph is showing a vertical asymptote at ![]() which tells us that the function is undefined at
which tells us that the function is undefined at ![]()
And as the inputs decrease without bound, the graph appears to be leveling off at output values of 4, indicating a horizontal asymptote at ![]() As the inputs increase without bound, the graph levels off at 4.
As the inputs increase without bound, the graph levels off at 4.
Try It
Use arrow notation to describe the end behavior and local behavior for the reciprocal squared function.
Show Solution
End behavior: as ![]() Local behavior: as
Local behavior: as ![]() (there are no x– or y-intercepts)
(there are no x– or y-intercepts)
Using Transformations to Graph a Rational Function
Sketch a graph of the reciprocal function shifted two units to the left and up three units. Identify the horizontal and vertical asymptotes of the graph, if any.
Show Solution
Shifting the graph left 2 and up 3 would result in the function
or equivalently, by giving the terms a common denominator,
The graph of the shifted function is displayed in (Figure).

Notice that this function is undefined at ![]() and the graph also is showing a vertical asymptote at
and the graph also is showing a vertical asymptote at ![]()
As the inputs increase and decrease without bound, the graph appears to be leveling off at output values of 3, indicating a horizontal asymptote at ![]()
Analysis
Notice that horizontal and vertical asymptotes are shifted left 2 and up 3 along with the function.
Try It
Sketch the graph, and find the horizontal and vertical asymptotes of the reciprocal squared function that has been shifted right 3 units and down 4 units.
Show Solution

The function and the asymptotes are shifted 3 units right and 4 units down. As ![]() and as
and as ![]()
The function is ![]()
Solving Applied Problems Involving Rational Functions
In (Figure), we shifted a toolkit function in a way that resulted in the function ![]() This is an example of a rational function. A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.
This is an example of a rational function. A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.
Rational Function
A rational function is a function that can be written as the quotient of two polynomial functions ![]()
Solving an Applied Problem Involving a Rational Function
A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the ratio of sugar to water, in pounds per gallon in the tank after 12 minutes. Is that a greater ratio of sugar to water, in pounds per gallon than at the beginning?
Show Solution
Let ![]() be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:
be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:
The ratio of sugar to water, in pounds per gallon, ![]() , will be the ratio of pounds of sugar to gallons of water
, will be the ratio of pounds of sugar to gallons of water
The ratio of sugar to water, in pounds per gallon after 12 minutes is given by evaluating ![]() at
at ![]()
This means the ratio of sugar to water, in pounds per gallon is 17 pounds of sugar to 220 gallons of water.
At the beginning, the ratio of sugar to water, in pounds per gallon is
Since ![]() the ratio of sugar to water, in pounds per gallon is greater after 12 minutes than at the beginning.
the ratio of sugar to water, in pounds per gallon is greater after 12 minutes than at the beginning.
Try It
There are 1,200 freshmen and 1,500 sophomores at a prep rally at noon. After 12 p.m., 20 freshmen arrive at the rally every five minutes while 15 sophomores leave the rally. Find the ratio of freshmen to sophomores at 1 p.m.
Show Solution
![]()
Finding the Domains of Rational Functions
A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.
Domain of a Rational Function
The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
How To
Given a rational function, find the domain.
- Set the denominator equal to zero.
- Solve to find the x-values that cause the denominator to equal zero.
- The domain is all real numbers except those found in Step 2.
Finding the Domain of a Rational Function
Find the domain of ![]()
Show Solution
Begin by setting the denominator equal to zero and solving.
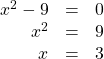
The denominator is equal to zero when ![]() The domain of the function is all real numbers except
The domain of the function is all real numbers except ![]()
Analysis
A graph of this function, as shown in (Figure), confirms that the function is not defined when ![]()

There is a vertical asymptote at ![]() and a hole in the graph at
and a hole in the graph at ![]() We will discuss these types of holes in greater detail later in this section.
We will discuss these types of holes in greater detail later in this section.
Try It
Find the domain of ![]()
Show Solution
The domain is all real numbers except ![]() and
and ![]()
Identifying Vertical Asymptotes of Rational Functions
By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.
Vertical Asymptotes
The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.
Given a rational function, identify any vertical asymptotes of its graph.
- Factor the numerator and denominator.
- Note any restrictions in the domain of the function.
- Reduce the expression by canceling common factors in the numerator and the denominator.
- Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
- Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities, or “holes.”
Identifying Vertical Asymptotes
Find the vertical asymptotes of the graph of ![]()
Show Solution
First, factor the numerator and denominator.

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:
Neither ![]() nor
nor ![]() are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph in (Figure) confirms the location of the two vertical asymptotes.
are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph in (Figure) confirms the location of the two vertical asymptotes.

Removable Discontinuities
Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.
For example, the function ![]() may be re-written by factoring the numerator and the denominator.
may be re-written by factoring the numerator and the denominator.
Notice that ![]() is a common factor to the numerator and the denominator. The zero of this factor,
is a common factor to the numerator and the denominator. The zero of this factor, ![]() is the location of the removable discontinuity. Notice also that
is the location of the removable discontinuity. Notice also that ![]() is not a factor in both the numerator and denominator. The zero of this factor,
is not a factor in both the numerator and denominator. The zero of this factor, ![]() is the vertical asymptote. See (Figure). [Note that removable discontinuities may not be visible when we use a graphing calculator, depending upon the window selected.]
is the vertical asymptote. See (Figure). [Note that removable discontinuities may not be visible when we use a graphing calculator, depending upon the window selected.]

Removable Discontinuities of Rational Functions
A removable discontinuity occurs in the graph of a rational function at ![]() if
if ![]() is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.
is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.
Identifying Vertical Asymptotes and Removable Discontinuities for a Graph
Find the vertical asymptotes and removable discontinuities of the graph of ![]()
Show Solution
Factor the numerator and the denominator.
Notice that there is a common factor in the numerator and the denominator, ![]() The zero for this factor is
The zero for this factor is ![]() This is the location of the removable discontinuity.
This is the location of the removable discontinuity.
Notice that there is a factor in the denominator that is not in the numerator, ![]() The zero for this factor is
The zero for this factor is ![]() The vertical asymptote is
The vertical asymptote is ![]() See (Figure).
See (Figure).

The graph of this function will have the vertical asymptote at ![]() but at
but at ![]() the graph will have a hole.
the graph will have a hole.
Try It
Find the vertical asymptotes and removable discontinuities of the graph of ![]()
Show Solution
Removable discontinuity at ![]() Vertical asymptotes:
Vertical asymptotes: ![]()
Identifying Horizontal Asymptotes of Rational Functions
While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms.
There are three distinct outcomes when checking for horizontal asymptotes:
Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at ![]()
In this case, the end behavior is ![]() This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function
This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function ![]() and the outputs will approach zero, resulting in a horizontal asymptote at
and the outputs will approach zero, resulting in a horizontal asymptote at ![]() See (Figure). Note that this graph crosses the horizontal asymptote.
See (Figure). Note that this graph crosses the horizontal asymptote.

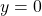 when
when 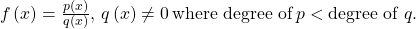
Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.
In this case, the end behavior is ![]() This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function
This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function ![]() As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of
As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of ![]() looks like a diagonal line, and since
looks like a diagonal line, and since ![]() will behave similarly to
will behave similarly to ![]() it will approach a line close to
it will approach a line close to ![]() This line is a slant asymptote.
This line is a slant asymptote.
To find the equation of the slant asymptote, divide ![]() The quotient is
The quotient is ![]() and the remainder is 2. The slant asymptote is the graph of the line
and the remainder is 2. The slant asymptote is the graph of the line ![]() See (Figure).
See (Figure).

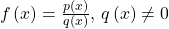 where degree of
where degree of 
Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at ![]() where
where ![]() and
and ![]() are the leading coefficients of
are the leading coefficients of ![]() and
and ![]() for
for ![]()
In this case, the end behavior is ![]() This tells us that as the inputs grow large, this function will behave like the function
This tells us that as the inputs grow large, this function will behave like the function ![]() which is a horizontal line. As
which is a horizontal line. As ![]() resulting in a horizontal asymptote at
resulting in a horizontal asymptote at ![]() See (Figure). Note that this graph crosses the horizontal asymptote.
See (Figure). Note that this graph crosses the horizontal asymptote.


Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.
It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function
with end behavior
the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.
Horizontal Asymptotes of Rational Functions
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
- Degree of numerator is less than degree of denominator: horizontal asymptote at

- Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
- Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.
Identifying Horizontal and Slant Asymptotes
For the functions listed, identify the horizontal or slant asymptote.
Show Solution
For these solutions, we will use ![]()
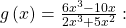 The degree of
The degree of 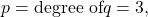 so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at
so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at  or
or 
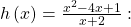 The degree of
The degree of 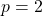 and degree of
and degree of 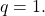 Since
Since 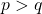 by 1, there is a slant asymptote found at
by 1, there is a slant asymptote found at 

The quotient is
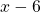 and the remainder is 13. There is a slant asymptote at
and the remainder is 13. There is a slant asymptote at 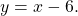
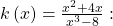 The degree of
The degree of 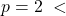 degree of
degree of 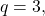 so there is a horizontal asymptote
so there is a horizontal asymptote 
Identifying Horizontal Asymptotes
In the sugar concentration problem earlier, we created the equation ![]()
Find the horizontal asymptote and interpret it in context of the problem.
Show Solution
Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is ![]() with coefficient 1. In the denominator, the leading term is
with coefficient 1. In the denominator, the leading term is ![]() with coefficient 10. The horizontal asymptote will be at the ratio of these values:
with coefficient 10. The horizontal asymptote will be at the ratio of these values:
This function will have a horizontal asymptote at ![]()
This tells us that as the values of t increase, the values of ![]() will approach
will approach ![]() In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or
In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or ![]() pounds per gallon.
pounds per gallon.
Identifying Horizontal and Vertical Asymptotes
Find the horizontal and vertical asymptotes of the function
Show Solution
First, note that this function has no common factors, so there are no potential removable discontinuities.
The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at ![]() indicating vertical asymptotes at these values.
indicating vertical asymptotes at these values.
The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as ![]() This function will have a horizontal asymptote at
This function will have a horizontal asymptote at ![]() See (Figure).
See (Figure).

Try It
Find the vertical and horizontal asymptotes of the function:
![]()
Show Solution
Vertical asymptotes at ![]() and
and ![]() horizontal asymptote at
horizontal asymptote at ![]()
Intercepts of Rational Functions
A rational function will have a y-intercept at ![]() , if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.
, if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.
Likewise, a rational function will have x-intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x-intercepts can only occur when the numerator of the rational function is equal to zero.
Finding the Intercepts of a Rational Function
Find the intercepts of ![]()
Show Solution
We can find the y-intercept by evaluating the function at zero
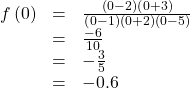
The x-intercepts will occur when the function is equal to zero:
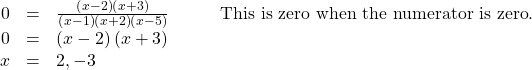
The y-intercept is ![]() the x-intercepts are
the x-intercepts are ![]() and
and ![]() See (Figure).
See (Figure).

Try It
Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x– and y-intercepts and the horizontal and vertical asymptotes.
Show Solution
For the transformed reciprocal squared function, we find the rational form. ![]()
Because the numerator is the same degree as the denominator we know that as ![]() is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is
is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is ![]() because as
because as ![]() We then set the numerator equal to 0 and find the x-intercepts are at
We then set the numerator equal to 0 and find the x-intercepts are at ![]() and
and ![]() Finally, we evaluate the function at 0 and find the y-intercept to be at
Finally, we evaluate the function at 0 and find the y-intercept to be at ![]()
Graphing Rational Functions
In (Figure), we see that the numerator of a rational function reveals the x-intercepts of the graph, whereas the denominator reveals the vertical asymptotes of the graph. As with polynomials, factors of the numerator may have integer powers greater than one. Fortunately, the effect on the shape of the graph at those intercepts is the same as we saw with polynomials.
The vertical asymptotes associated with the factors of the denominator will mirror one of the two toolkit reciprocal functions. When the degree of the factor in the denominator is odd, the distinguishing characteristic is that on one side of the vertical asymptote the graph heads towards positive infinity, and on the other side the graph heads towards negative infinity. See (Figure).

When the degree of the factor in the denominator is even, the distinguishing characteristic is that the graph either heads toward positive infinity on both sides of the vertical asymptote or heads toward negative infinity on both sides. See (Figure).

For example, the graph of ![]() is shown in (Figure).
is shown in (Figure).

- At the x-intercept
 corresponding to the
corresponding to the 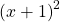 factor of the numerator, the graph “bounces”, consistent with the quadratic nature of the factor.
factor of the numerator, the graph “bounces”, consistent with the quadratic nature of the factor. - At the x-intercept
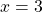 corresponding to the
corresponding to the 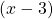 factor of the numerator, the graph passes through the axis as we would expect from a linear factor.
factor of the numerator, the graph passes through the axis as we would expect from a linear factor. - At the vertical asymptote
 corresponding to the
corresponding to the 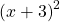 factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function
factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function 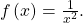
- At the vertical asymptote
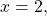 corresponding to the
corresponding to the  factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side, consistent with the behavior of the function
factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side, consistent with the behavior of the function 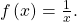
How To
Given a rational function, sketch a graph.
- Evaluate the function at 0 to find the y-intercept.
- Factor the numerator and denominator.
- For factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the x-intercepts.
- Find the multiplicities of the x-intercepts to determine the behavior of the graph at those points.
- For factors in the denominator, note the multiplicities of the zeros to determine the local behavior. For those factors not common to the numerator, find the vertical asymptotes by setting those factors equal to zero and then solve.
- For factors in the denominator common to factors in the numerator, find the removable discontinuities by setting those factors equal to 0 and then solve.
- Compare the degrees of the numerator and the denominator to determine the horizontal or slant asymptotes.
- Sketch the graph.
Graphing a Rational Function
Sketch a graph of ![]()
Show Solution
We can start by noting that the function is already factored, saving us a step.
Next, we will find the intercepts. Evaluating the function at zero gives the y-intercept:
To find the x-intercepts, we determine when the numerator of the function is zero. Setting each factor equal to zero, we find x-intercepts at ![]() and
and ![]() At each, the behavior will be linear (multiplicity 1), with the graph passing through the intercept.
At each, the behavior will be linear (multiplicity 1), with the graph passing through the intercept.
We have a y-intercept at ![]() and x-intercepts at
and x-intercepts at ![]() and
and ![]()
To find the vertical asymptotes, we determine when the denominator is equal to zero. This occurs when ![]() and when
and when ![]() giving us vertical asymptotes at
giving us vertical asymptotes at ![]() and
and ![]()
There are no common factors in the numerator and denominator. This means there are no removable discontinuities.
Finally, the degree of denominator is larger than the degree of the numerator, telling us this graph has a horizontal asymptote at ![]()
To sketch the graph, we might start by plotting the three intercepts. Since the graph has no x-intercepts between the vertical asymptotes, and the y-intercept is positive, we know the function must remain positive between the asymptotes, letting us fill in the middle portion of the graph as shown in (Figure).

The factor associated with the vertical asymptote at ![]() was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.
was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.
For the vertical asymptote at ![]() the factor was not squared, so the graph will have opposite behavior on either side of the asymptote. See (Figure). After passing through the x-intercepts, the graph will then level off toward an output of zero, as indicated by the horizontal asymptote.
the factor was not squared, so the graph will have opposite behavior on either side of the asymptote. See (Figure). After passing through the x-intercepts, the graph will then level off toward an output of zero, as indicated by the horizontal asymptote.

Try It
Given the function ![]() use the characteristics of polynomials and rational functions to describe its behavior and sketch the function.
use the characteristics of polynomials and rational functions to describe its behavior and sketch the function.
Show Solution
Horizontal asymptote at ![]() Vertical asymptotes at
Vertical asymptotes at ![]() y-intercept at
y-intercept at ![]()
x-intercepts at ![]()
![]() is a zero with multiplicity 2, and the graph bounces off the x-axis at this point.
is a zero with multiplicity 2, and the graph bounces off the x-axis at this point. ![]() is a single zero and the graph crosses the axis at this point.
is a single zero and the graph crosses the axis at this point.

Writing Rational Functions
Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x-intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x-intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.
Writing Rational Functions from Intercepts and Asymptotes
If a rational function has x-intercepts at ![]() vertical asymptotes at
vertical asymptotes at ![]() and no
and no ![]() then the function can be written in the form:
then the function can be written in the form:
where the powers ![]() or
or ![]() on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor
on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor ![]() can be determined given a value of the function other than the x-intercept or by the horizontal asymptote if it is nonzero.
can be determined given a value of the function other than the x-intercept or by the horizontal asymptote if it is nonzero.
How To
Given a graph of a rational function, write the function.
- Determine the factors of the numerator. Examine the behavior of the graph at the x-intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the “simplest” function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
- Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
- Use any clear point on the graph to find the stretch factor.
Writing a Rational Function from Intercepts and Asymptotes
Write an equation for the rational function shown in (Figure).

Show Solution
The graph appears to have x-intercepts at ![]() and
and ![]() At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at
At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at ![]() seems to exhibit the basic behavior similar to
seems to exhibit the basic behavior similar to ![]() with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at
with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at ![]() is exhibiting a behavior similar to
is exhibiting a behavior similar to ![]() with the graph heading toward negative infinity on both sides of the asymptote. See (Figure).
with the graph heading toward negative infinity on both sides of the asymptote. See (Figure).

We can use this information to write a function of the form
To find the stretch factor, we can use another clear point on the graph, such as the y-intercept ![]()
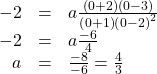
This gives us a final function of ![]()
Access these online resources for additional instruction and practice with rational functions.
Key Equations
| Rational Function |
Key Concepts
- We can use arrow notation to describe local behavior and end behavior of the toolkit functions
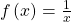 and
and 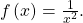 See (Figure).
See (Figure). - A function that levels off at a horizontal value has a horizontal asymptote. A function can have more than one vertical asymptote. See (Figure).
- Application problems involving rates and concentrations often involve rational functions. See (Figure).
- The domain of a rational function includes all real numbers except those that cause the denominator to equal zero. See (Figure).
- The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero. See (Figure).
- A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero. See (Figure).
- A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions. See (Figure), (Figure), (Figure), and (Figure).
- Graph rational functions by finding the intercepts, behavior at the intercepts and asymptotes, and end behavior. See (Figure).
- If a rational function has x-intercepts at
 vertical asymptotes at
vertical asymptotes at 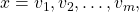 and no
and no 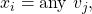 then the function can be written in the form
then the function can be written in the form
See (Figure).
Section Exercises
Verbal
1. What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?
Show Solution
The rational function will be represented by a quotient of polynomial functions.
2. What is the fundamental difference in the graphs of polynomial functions and rational functions?
3. If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?
Show Solution
The numerator and denominator must have a common factor.
4. Can a graph of a rational function have no vertical asymptote? If so, how?
5. Can a graph of a rational function have no x-intercepts? If so, how?
Show Solution
Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator.
Algebraic
For the following exercises, find the domain of the rational functions.
6. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
For the following exercises, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.
10. ![]()
11. ![]()
Show Solution
V.A. at ![]() H.A. at
H.A. at ![]() Domain is all reals
Domain is all reals ![]()
12. ![]()
13. ![]()
Show Solution
V.A. at ![]() H.A. at
H.A. at ![]() Domain is all reals
Domain is all reals ![]()
14. ![]()
15. ![]()
Show Solution
V.A. at ![]() H.A. at
H.A. at ![]() Domain is all reals
Domain is all reals ![]()
16. ![]()
17. ![]()
Show Solution
V.A. at ![]() H.A. at
H.A. at ![]() Domain is all reals
Domain is all reals ![]()
18. ![]()
19. ![]()
Show Solution
V.A. at ![]() H.A. at
H.A. at ![]() Domain is all reals
Domain is all reals ![]()
For the following exercises, find the x– and y-intercepts for the functions.
20. ![]()
21. ![]()
Show Solution
none
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
For the following exercises, describe the local and end behavior of the functions.
25. ![]()
Show Solution
Local behavior: ![]()
End behavior: ![]()
26. ![]()
27. ![]()
Show Solution
Local behavior: ![]() End behavior:
End behavior: ![]()
28. ![]()
29. ![]()
Show Solution
Local behavior: ![]()
![]()
End behavior: ![]()
For the following exercises, find the slant asymptote of the functions.
30. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
Graphical
For the following exercises, use the given transformation to graph the function. Note the vertical and horizontal asymptotes.
35. The reciprocal function shifted up two units.
Show Solution
![]()

36. The reciprocal function shifted down one unit and left three units.
37. The reciprocal squared function shifted to the right 2 units.
Show Solution
![]()

38. The reciprocal squared function shifted down 2 units and right 1 unit.
For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.
Show Solution
![]()

40. ![]()
Show Solution
![]()

42. ![]()
43. ![]()
Show Solution
![]()

44. ![]()
45. ![]()
Show Solution
![]()

46. ![]()
47. ![]()
Show Solution
![]()

48. ![]()
49. ![]()
Show Solution
![]()

50. ![]()
For the following exercises, write an equation for a rational function with the given characteristics.
51. Vertical asymptotes at ![]() and
and ![]() x-intercepts at
x-intercepts at ![]() and
and ![]() y-intercept at
y-intercept at ![]()
Show Solution
![]()
52. Vertical asymptotes at ![]() and
and ![]() x-intercepts at
x-intercepts at ![]() and
and ![]() y-intercept at
y-intercept at ![]()
53. Vertical asymptotes at ![]() and
and ![]() x-intercepts at
x-intercepts at ![]() and
and ![]() Horizontal asymptote at
Horizontal asymptote at ![]()
Show Solution
![]()
54. Vertical asymptotes at ![]() and
and ![]() x-intercepts at
x-intercepts at ![]() and
and ![]() Horizontal asymptote at
Horizontal asymptote at ![]()
55. Vertical asymptote at ![]() Double zero at
Double zero at ![]() y-intercept at
y-intercept at ![]()
Show Solution
![]()
56. Vertical asymptote at ![]() Double zero at
Double zero at ![]() y-intercept at
y-intercept at ![]()
For the following exercises, use the graphs to write an equation for the function.

Show Solution
![]()
58. 

Show Solution
![]()
60. 

Show Solution
![]()
62. 

Show Solution
![]()

Numeric
For the following exercises, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote
65. ![]()
Show Solution
| 2.01 | 2.001 | 2.0001 | 1.99 | 1.999 | |
| 100 | 1,000 | 10,000 | –100 | –1,000 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
|---|---|---|---|---|---|
| .125 | .0102 | .001 | .0001 | .00001 |
Vertical asymptote ![]() Horizontal asymptote
Horizontal asymptote ![]()
67. ![]()
Show Solution
| –4.1 | –4.01 | –4.001 | –3.99 | –3.999 | |
| 82 | 802 | 8,002 | –798 | –7998 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
| 1.4286 | 1.9331 | 1.992 | 1.9992 | 1.999992 |
Vertical asymptote ![]() Horizontal asymptote
Horizontal asymptote ![]()
68. ![]()
69. ![]()
Show Solution
| –.9 | –.99 | –.999 | –1.1 | –1.01 | |
| 81 | 9,801 | 998,001 | 121 | 10,201 |
| 10 | 100 | 1,000 | 10,000 | 100,000 | |
| .82645 | .9803 | .998 | .9998 |
Vertical asymptote ![]() Horizontal asymptote
Horizontal asymptote ![]()
Technology
For the following exercises, use a calculator to graph ![]() Use the graph to solve
Use the graph to solve ![]()
70. ![]()
71. ![]()
Show Solution
![]()

72. ![]()
73. ![]()
Show Solution
![]()

74. ![]()
Extensions
For the following exercises, identify the removable discontinuity.
75. ![]()
Show Solution
![]()
76. ![]()
77. ![]()
Show Solution
![]()
78. ![]()
79. ![]()
Show Solution
![]()
Real-World Applications
For the following exercises, express a rational function that describes the situation.
80. A large mixing tank currently contains 200 gallons of water, into which 10 pounds of sugar have been mixed. A tap will open, pouring 10 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 3 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after ![]() minutes.
minutes.
81. A large mixing tank currently contains 300 gallons of water, into which 8 pounds of sugar have been mixed. A tap will open, pouring 20 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 2 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after ![]() minutes.
minutes.
Show Solution
![]()
For the following exercises, use the given rational function to answer the question.
82. The concentration ![]() of a drug in a patient’s bloodstream
of a drug in a patient’s bloodstream ![]() hours after injection in given by
hours after injection in given by ![]() What happens to the concentration of the drug as
What happens to the concentration of the drug as ![]() increases?
increases?
83. The concentration ![]() of a drug in a patient’s bloodstream
of a drug in a patient’s bloodstream ![]() hours after injection is given by
hours after injection is given by ![]() Use a calculator to approximate the time when the concentration is highest.
Use a calculator to approximate the time when the concentration is highest.
Show Solution
After about 6.12 hours.
For the following exercises, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.
84. An open box with a square base is to have a volume of 108 cubic inches. Find the dimensions of the box that will have minimum surface area. Let ![]() = length of the side of the base.
= length of the side of the base.
85. A rectangular box with a square base is to have a volume of 20 cubic feet. The material for the base costs 30 cents/ square foot. The material for the sides costs 10 cents/square foot. The material for the top costs 20 cents/square foot. Determine the dimensions that will yield minimum cost. Let ![]() = length of the side of the base.
= length of the side of the base.
Show Solution
![]() 2 by 2 by 5 feet.
2 by 2 by 5 feet.
86. A right circular cylinder has volume of 100 cubic inches. Find the radius and height that will yield minimum surface area. Let ![]() = radius.
= radius.
87. A right circular cylinder with no top has a volume of 50 cubic meters. Find the radius that will yield minimum surface area. Let ![]() = radius.
= radius.
Show Solution
![]() Radius = 2.52 meters.
Radius = 2.52 meters.
88. A right circular cylinder is to have a volume of 40 cubic inches. It costs 4 cents/square inch to construct the top and bottom and 1 cent/square inch to construct the rest of the cylinder. Find the radius to yield minimum cost. Let ![]() = radius.
= radius.
Glossary
- arrow notation
- a way to represent symbolically the local and end behavior of a function by using arrows to indicate that an input or output approaches a value
- horizontal asymptote
- a horizontal line
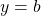 where the graph approaches the line as the inputs increase or decrease without bound.
where the graph approaches the line as the inputs increase or decrease without bound.
- rational function
- a function that can be written as the ratio of two polynomials
- removable discontinuity
- a single point at which a function is undefined that, if filled in, would make the function continuous; it appears as a hole on the graph of a function
- vertical asymptote
- a vertical line
 where the graph tends toward positive or negative infinity as the inputs approach
where the graph tends toward positive or negative infinity as the inputs approach 

