Chapter 3.4: Unit Circle
Learning Objectives
In this section you will:
- Find function values for the sine and cosine of
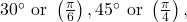 and
and 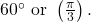
- Identify the domain and range of sine and cosine functions.
- Find reference angles.
- Use reference angles to evaluate trigonometric functions.

Looking for a thrill? Then consider a ride on the Singapore Flyer, the world’s tallest Ferris wheel. Located in Singapore, the Ferris wheel soars to a height of 541 feet—a little more than a tenth of a mile! Described as an observation wheel, riders enjoy spectacular views as they travel from the ground to the peak and down again in a repeating pattern. In this section, we will examine this type of revolving motion around a circle. To do so, we need to define the type of circle first, and then place that circle on a coordinate system. Then we can discuss circular motion in terms of the coordinate pairs.
Finding Trigonometric Functions Using the Unit Circle
We have already defined the trigonometric functions in terms of right triangles. In this section, we will redefine them in terms of the unit circle. Recall that a unit circle is a circle centered at the origin with radius 1, as shown in (Figure). The angle (in radians) that ![]() intercepts forms an arc of length
intercepts forms an arc of length ![]() Using the formula
Using the formula ![]() and knowing that
and knowing that ![]() we see that for a unit circle,
we see that for a unit circle, ![]()
The x- and y-axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.
For any angle ![]() we can label the intersection of the terminal side and the unit circle as by its coordinates,
we can label the intersection of the terminal side and the unit circle as by its coordinates, ![]() The coordinates
The coordinates ![]() and
and ![]() will be the outputs of the trigonometric functions
will be the outputs of the trigonometric functions ![]() and
and ![]() respectively. This means
respectively. This means ![]() and
and ![]()

Unit Circle
A unit circle has a center at ![]() and radius
and radius ![]() In a unit circle, the length of the intercepted arc is equal to the radian measure of the central angle
In a unit circle, the length of the intercepted arc is equal to the radian measure of the central angle ![]()
Let ![]() be the endpoint on the unit circle of an arc of arc length
be the endpoint on the unit circle of an arc of arc length ![]() The
The ![]() coordinates of this point can be described as functions of the angle.
coordinates of this point can be described as functions of the angle.
Defining Sine and Cosine Functions from the Unit Circle
The sine function relates a real number ![]() to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle
to the y-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle ![]() equals the y-value of the endpoint on the unit circle of an arc of length
equals the y-value of the endpoint on the unit circle of an arc of length ![]() In (Figure), the sine is equal to
In (Figure), the sine is equal to ![]() Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the y-coordinate of the corresponding point on the unit circle.
Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the y-coordinate of the corresponding point on the unit circle.
The cosine function of an angle ![]() equals the x-value of the endpoint on the unit circle of an arc of length
equals the x-value of the endpoint on the unit circle of an arc of length ![]() In (Figure), the cosine is equal to
In (Figure), the cosine is equal to ![]()

Because it is understood that sine and cosine are functions, we do not always need to write them with parentheses: ![]() is the same as
is the same as ![]() and
and ![]() is the same as
is the same as ![]() Likewise,
Likewise, ![]() is a commonly used shorthand notation for
is a commonly used shorthand notation for ![]() Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.
Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.
Sine and Cosine Functions
If ![]() is a real number and a point
is a real number and a point ![]() on the unit circle corresponds to a central angle
on the unit circle corresponds to a central angle ![]() then
then
How To
Given a point P ![]() on the unit circle corresponding to an angle of
on the unit circle corresponding to an angle of ![]() find the sine and cosine.
find the sine and cosine.
- The sine of
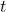 is equal to the y-coordinate of point
is equal to the y-coordinate of point 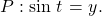
- The cosine of
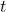 is equal to the x-coordinate of point
is equal to the x-coordinate of point 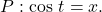
Finding Function Values for Sine and Cosine
Point ![]() is a point on the unit circle corresponding to an angle of
is a point on the unit circle corresponding to an angle of ![]() as shown in (Figure). Find
as shown in (Figure). Find ![]() and
and ![]()
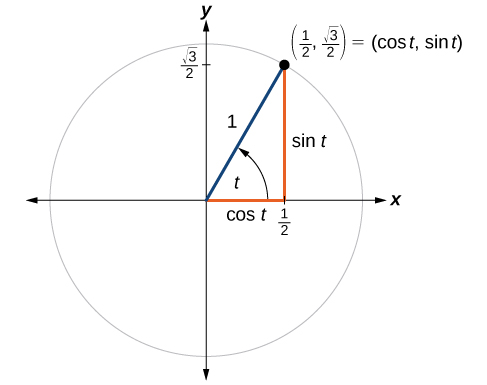
Show Solution
We know that ![]() is the x-coordinate of the corresponding point on the unit circle and
is the x-coordinate of the corresponding point on the unit circle and ![]() is the y-coordinate of the corresponding point on the unit circle. So:
is the y-coordinate of the corresponding point on the unit circle. So:
Try It
A certain angle ![]() corresponds to a point on the unit circle at
corresponds to a point on the unit circle at ![]() as shown in (Figure). Find
as shown in (Figure). Find ![]() and
and ![]()
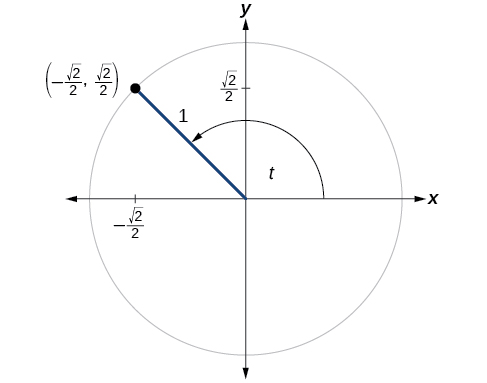
Show Solution
![]()
Finding Sines and Cosines of Angles on an Axis
For quadrantal angles, the corresponding point on the unit circle falls on the x- or y-axis. In that case, we can easily calculate cosine and sine from the values of ![]() and
and ![]()
Calculating Sines and Cosines along an Axis
Find ![]() and
and ![]()
Show Solution
Moving ![]() counterclockwise around the unit circle from the positive x-axis brings us to the top of the circle, where the
counterclockwise around the unit circle from the positive x-axis brings us to the top of the circle, where the ![]() coordinates are
coordinates are ![]() as shown in (Figure).
as shown in (Figure).

We can then use our definitions of cosine and sine.
The cosine of ![]() is 0; the sine of
is 0; the sine of ![]() is 1.
is 1.
Try It
Find cosine and sine of the angle ![]()
Show Solution
![]()
The Pythagorean Identity
Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is ![]() Because
Because ![]() and
and ![]() we can substitute for
we can substitute for ![]() and
and ![]() to get
to get ![]() This equation,
This equation, ![]() is known as the Pythagorean Identity. See (Figure).
is known as the Pythagorean Identity. See (Figure).

We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.
Pythagorean Identity
The Pythagorean Identity states that, for any real number ![]()
How To
Given the sine of some angle ![]() and its quadrant location, find the cosine of
and its quadrant location, find the cosine of ![]()
- Substitute the known value of
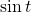 into the Pythagorean Identity.
into the Pythagorean Identity. - Solve for
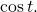
- Choose the solution with the appropriate sign for the x-values in the quadrant where
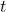 is located.
is located.
Finding a Cosine from a Sine or a Sine from a Cosine
If ![]() and
and ![]() is in the second quadrant, find
is in the second quadrant, find ![]()
Show Solution
If we drop a vertical line from the point on the unit circle corresponding to ![]() we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem. See (Figure).
we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem. See (Figure).

Substituting the known value for sine into the Pythagorean Identity,
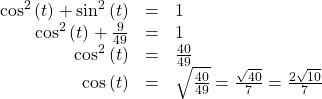
Because the angle is in the second quadrant, we know the x-value is a negative real number, so the cosine is also negative.
Try It
If ![]() and
and ![]() is in the fourth quadrant, find
is in the fourth quadrant, find ![]()
Show Solution
![]()
Finding Sines and Cosines of Special Angles
We have already learned some properties of the special angles, such as the conversion from radians to degrees, and we found their sines and cosines using right triangles. We can also calculate sines and cosines of the special angles using the Pythagorean Identity.
Finding Sines and Cosines of 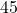 Angles
Angles
First, we will look at angles of ![]() or
or ![]() as shown in (Figure). A
as shown in (Figure). A ![]() triangle is an isosceles triangle, so the x- and y-coordinates of the corresponding point on the circle are the same. Because the x- and y-values are the same, the sine and cosine values will also be equal.
triangle is an isosceles triangle, so the x- and y-coordinates of the corresponding point on the circle are the same. Because the x- and y-values are the same, the sine and cosine values will also be equal.

At ![]() which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line
which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line ![]() A unit circle has a radius equal to 1 so the right triangle formed below the line
A unit circle has a radius equal to 1 so the right triangle formed below the line ![]() has sides
has sides ![]() and
and ![]() and radius = 1. See (Figure).
and radius = 1. See (Figure).

From the Pythagorean Theorem we get
We can then substitute ![]()
Next we combine like terms.
And solving for ![]() we get
we get
In quadrant I, ![]()
At ![]() or 45 degrees,
or 45 degrees,
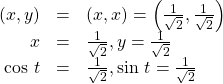
If we then rationalize the denominators, we get
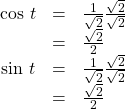
Therefore, the ![]() coordinates of a point on a circle of radius
coordinates of a point on a circle of radius ![]() at an angle of
at an angle of ![]() are
are ![]()
Finding Sines and Cosines of 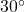 and
and  Angles
Angles
Next, we will find the cosine and sine at an angle of ![]() or
or ![]() First, we will draw a triangle inside a circle with one side at an angle of
First, we will draw a triangle inside a circle with one side at an angle of ![]() and another at an angle of
and another at an angle of ![]() as shown in (Figure). If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be
as shown in (Figure). If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be ![]() as shown in (Figure).
as shown in (Figure).

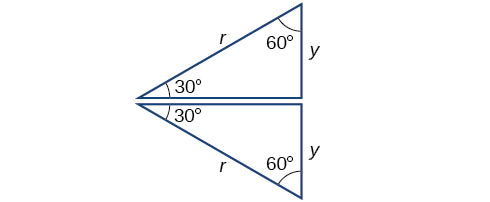
Because all the angles are equal, the sides are also equal. The vertical line has length ![]() and since the sides are all equal, we can also conclude that
and since the sides are all equal, we can also conclude that ![]() or
or ![]() Since
Since ![]()
And since ![]() in our unit circle,
in our unit circle,
Using the Pythagorean Identity, we can find the cosine value.

The ![]() coordinates for the point on a circle of radius
coordinates for the point on a circle of radius ![]() at an angle of
at an angle of ![]() are
are ![]() At
At ![]() the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle,
the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle, ![]() as shown in (Figure). Angle
as shown in (Figure). Angle ![]() has measure
has measure ![]() At point
At point ![]() we draw an angle
we draw an angle ![]() with measure of
with measure of ![]() We know the angles in a triangle sum to
We know the angles in a triangle sum to ![]() so the measure of angle
so the measure of angle ![]() is also
is also ![]() Now we have an equilateral triangle. Because each side of the equilateral triangle
Now we have an equilateral triangle. Because each side of the equilateral triangle ![]() is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.
is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.

The measure of angle ![]() is
is ![]() Angle
Angle ![]() is double angle
is double angle ![]() so its measure is
so its measure is ![]()
![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() so it cuts
so it cuts ![]() in half. This means that
in half. This means that ![]() is
is ![]() the radius, or
the radius, or ![]() Notice that
Notice that ![]() is the x-coordinate of point
is the x-coordinate of point ![]() which is at the intersection of the 60° angle and the unit circle. This gives us a triangle
which is at the intersection of the 60° angle and the unit circle. This gives us a triangle ![]() with hypotenuse of 1 and side
with hypotenuse of 1 and side ![]() of length
of length ![]()
From the Pythagorean Theorem, we get
Substituting ![]() we get
we get
Solving for ![]() we get
we get
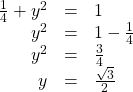
Since ![]() has the terminal side in quadrant I where the y-coordinate is positive, we choose
has the terminal side in quadrant I where the y-coordinate is positive, we choose ![]() the positive value.
the positive value.
At ![]() (60°), the
(60°), the ![]() coordinates for the point on a circle of radius
coordinates for the point on a circle of radius ![]() at an angle of
at an angle of ![]() are
are ![]() so we can find the sine and cosine.
so we can find the sine and cosine.
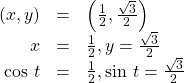
We have now found the cosine and sine values for all of the most commonly encountered angles in the first quadrant of the unit circle. (Figure) summarizes these values.
| Angle | |||||
| Cosine | 1 | 0 | |||
| Sine | 0 | 1 |
(Figure) shows the common angles in the first quadrant of the unit circle.
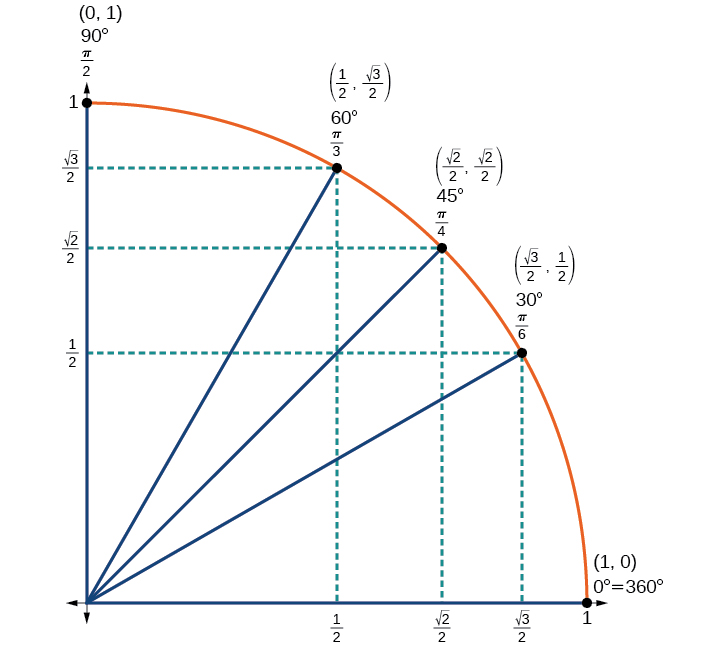
Using a Calculator to Find Sine and Cosine
To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware: Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate ![]() on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.
on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.
How To
Given an angle in radians, use a graphing calculator to find the cosine.
- If the calculator has degree mode and radian mode, set it to radian mode.
- Press the COS key.
- Enter the radian value of the angle and press the close-parentheses key “)”.
- Press ENTER.
Using a Graphing Calculator to Find Sine and Cosine
Evaluate ![]() using a graphing calculator or computer.
using a graphing calculator or computer.
Show Solution
Enter the following keystrokes:
![]()
Analysis
We can find the cosine or sine of an angle in degrees directly on a calculator with degree mode. For calculators or software that use only radian mode, we can find the sign of ![]() for example, by including the conversion factor to radians as part of the input:
for example, by including the conversion factor to radians as part of the input:
Try It
Evaluate ![]()
Show Solution
approximately 0.866025403
Identifying the Domain and Range of Sine and Cosine Functions
Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that can be inputs of the functions? Because angles smaller than ![]() and angles larger than
and angles larger than ![]() can still be graphed on the unit circle and have real values of
can still be graphed on the unit circle and have real values of ![]() there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive x-axis, and that may be any real number.
there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive x-axis, and that may be any real number.
What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in (Figure). The bounds of the x-coordinate are ![]() The bounds of the y-coordinate are also
The bounds of the y-coordinate are also ![]() Therefore, the range of both the sine and cosine functions is
Therefore, the range of both the sine and cosine functions is ![]()

Finding Reference Angles
We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but have the opposite x-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.
Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same x-value but will have the opposite y-value. Therefore, its sine value will be the opposite of the original angle’s sine value.
As shown in (Figure), angle ![]() has the same sine value as angle
has the same sine value as angle ![]() the cosine values are opposites. Angle
the cosine values are opposites. Angle ![]() has the same cosine value as angle
has the same cosine value as angle ![]() the sine values are opposites.
the sine values are opposites.

Recall that an angle’s reference angle is the acute angle, ![]() formed by the terminal side of the angle
formed by the terminal side of the angle ![]() and the horizontal axis. A reference angle is always an angle between
and the horizontal axis. A reference angle is always an angle between ![]() and
and ![]() or
or ![]() and
and ![]() radians. As we can see from (Figure), for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.
radians. As we can see from (Figure), for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

How To
Given an angle between ![]() and
and ![]() find its reference angle.
find its reference angle.
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is
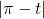 or
or 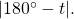
- For an angle in the fourth quadrant, the reference angle is
 or
or 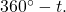
- If an angle is less than
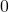 or greater than
or greater than 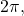 add or subtract
add or subtract 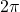 as many times as needed to find an equivalent angle between
as many times as needed to find an equivalent angle between 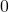 and
and 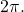
Show Solution
Because ![]() is in the third quadrant, the reference angle is
is in the third quadrant, the reference angle is
Try It
Find the reference angle of ![]()
Show Solution
![]()
Using Reference Angles
Now let’s take a moment to reconsider the Ferris wheel introduced at the beginning of this section. Suppose a rider snaps a photograph while stopped twenty feet above ground level. The rider then rotates three-quarters of the way around the circle. What is the rider’s new elevation? To answer questions such as this one, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find ![]() coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.
coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.
Using Reference Angles to Evaluate Trigonometric Functions
We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the x-values in that quadrant. The sine will be positive or negative depending on the sign of the y-values in that quadrant.
Using Reference Angles to Find Cosine and Sine
Angles have cosines and sines with the same absolute value as their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.
How To
Given an angle in standard position, find the reference angle, and the cosine and sine of the original angle.
- Measure the angle between the terminal side of the given angle and the horizontal axis. That is the reference angle.
- Determine the values of the cosine and sine of the reference angle.
- Give the cosine the same sign as the x-values in the quadrant of the original angle.
- Give the sine the same sign as the y-values in the quadrant of the original angle.
Using Reference Angles to Find Sine and Cosine
- Using a reference angle, find the exact value of
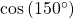 and
and 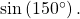
- Using the reference angle, find
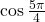 and
and 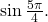
Show Solution
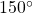 is located in the second quadrant. The angle it makes with the x-axis is
is located in the second quadrant. The angle it makes with the x-axis is 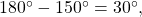 so the reference angle is
so the reference angle is 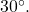
This tells us that
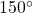 has the same sine and cosine values as
has the same sine and cosine values as 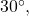 except for the sign.
except for the sign.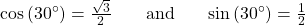
Since
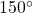 is in the second quadrant, the x-coordinate of the point on the circle is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.
is in the second quadrant, the x-coordinate of the point on the circle is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.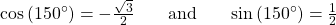
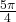 is in the third quadrant. Its reference angle is
is in the third quadrant. Its reference angle is 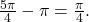 The cosine and sine of
The cosine and sine of 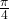 are both
are both 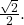 In the third quadrant, both
In the third quadrant, both 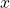 and
and 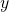 are negative, so:
are negative, so:
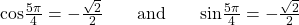
Try It
- Use the reference angle of
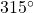 to find
to find 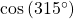 and
and 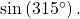
- Use the reference angle of
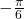 to find
to find 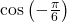 and
and 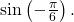
Show Solution
Using Reference Angles to Find Coordinates
Now that we have learned how to find the cosine and sine values for special angles in the first quadrant, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle. They are shown in (Figure). Take time to learn the ![]() coordinates of all of the major angles in the first quadrant.
coordinates of all of the major angles in the first quadrant.

In addition to learning the values for special angles, we can use reference angles to find ![]() coordinates of any point on the unit circle, using what we know of reference angles along with the identities
coordinates of any point on the unit circle, using what we know of reference angles along with the identities
First we find the reference angle corresponding to the given angle. Then we take the sine and cosine values of the reference angle, and give them the signs corresponding to the y– and x-values of the quadrant.
How To
Given the angle of a point on a circle and the radius of the circle, find the ![]() coordinates of the point.
coordinates of the point.
- Find the reference angle by measuring the smallest angle to the x-axis.
- Find the cosine and sine of the reference angle.
- Determine the appropriate signs for
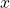 and
and 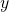 in the given quadrant.
in the given quadrant.
Using the Unit Circle to Find Coordinates
Find the coordinates of the point on the unit circle at an angle of ![]()
Show Solution
We know that the angle ![]() is in the third quadrant.
is in the third quadrant.
First, let’s find the reference angle by measuring the angle to the x-axis. To find the reference angle of an angle whose terminal side is in quadrant III, we find the difference of the angle and ![]()
Next, we will find the cosine and sine of the reference angle.
We must determine the appropriate signs for x and y in the given quadrant. Because our original angle is in the third quadrant, where both ![]() and
and ![]() are negative, both cosine and sine are negative.
are negative, both cosine and sine are negative.
Now we can calculate the ![]() coordinates using the identities
coordinates using the identities ![]() and
and ![]()
The coordinates of the point are ![]() on the unit circle.
on the unit circle.
Try It
Find the coordinates of the point on the unit circle at an angle of ![]()
Show Solution
![]()
Access these online resources for additional instruction and practice with sine and cosine functions.
Key Equations
| Cosine | |
| Sine | |
| Pythagorean Identity |
Key Concepts
- Finding the function values for the sine and cosine begins with drawing a unit circle, which is centered at the origin and has a radius of 1 unit.
- Using the unit circle, the sine of an angle
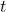 equals the y-value of the endpoint on the unit circle of an arc of length
equals the y-value of the endpoint on the unit circle of an arc of length 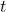 whereas the cosine of an angle
whereas the cosine of an angle 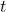 equals the x-value of the endpoint. See (Figure).
equals the x-value of the endpoint. See (Figure). - The sine and cosine values are most directly determined when the corresponding point on the unit circle falls on an axis. See (Figure).
- When the sine or cosine is known, we can use the Pythagorean Identity to find the other. The Pythagorean Identity is also useful for determining the sines and cosines of special angles. See (Figure).
- Calculators and graphing software are helpful for finding sines and cosines if the proper procedure for entering information is known. See (Figure).
- The domain of the sine and cosine functions is all real numbers.
- The range of both the sine and cosine functions is
![Rendered by QuickLaTeX.com \,\left[-1,1\right].](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-910e5af71e23d02faf3e224d246587d1_l3.png)
- The sine and cosine of an angle have the same absolute value as the sine and cosine of its reference angle.
- The signs of the sine and cosine are determined from the x– and y-values in the quadrant of the original angle.
- An angle’s reference angle is the size angle,
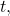 formed by the terminal side of the angle
formed by the terminal side of the angle 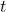 and the horizontal axis. See (Figure).
and the horizontal axis. See (Figure). - Reference angles can be used to find the sine and cosine of the original angle. See (Figure).
- Reference angles can also be used to find the coordinates of a point on a circle. See (Figure).
Section Exercises
Verbal
1. Describe the unit circle.
Show Solution
The unit circle is a circle of radius 1 centered at the origin.
2. What do the x- and y-coordinates of the points on the unit circle represent?
3. Discuss the difference between a coterminal angle and a reference angle.
Show Solution
Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, ![]() formed by the terminal side of the angle
formed by the terminal side of the angle ![]() and the horizontal axis.
and the horizontal axis.
4. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.
5. Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.
Show Solution
The sine values are equal.
Algebraic
For the following exercises, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by ![]() lies.
lies.
6. ![]() and
and ![]()
7. ![]() and
and ![]()
Show Solution
I
8. ![]() and
and ![]()
9. ![]() and
and ![]()
Show Solution
IV
For the following exercises, find the exact value of each trigonometric function.
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
![]()
14. ![]()
15. ![]()
Show Solution
![]()
16. ![]()
17. ![]()
Show Solution
0
18. ![]()
19. ![]()
Show Solution
-1
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
Numeric
For the following exercises, state the reference angle for the given angle.
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
![]()
26. ![]()
27. ![]()
Show Solution
![]()
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.
40. ![]()
41. ![]()
Show Solution
![]() Quadrant IV,
Quadrant IV, ![]()
42. ![]()
43. ![]()
Show Solution
![]() Quadrant II,
Quadrant II, ![]()
44. ![]()
45. ![]()
Show Solution
![]() Quadrant II,
Quadrant II, ![]()
46. ![]()
47. ![]()
Show Solution
![]() Quadrant II,
Quadrant II, ![]()
48. ![]()
49. ![]()
Show Solution
![]() Quadrant III,
Quadrant III, ![]()
50. ![]()
51. ![]()
Show Solution
![]() Quadrant II,
Quadrant II, ![]()
52. ![]()
53. ![]()
Show Solution
![]() Quadrant II,
Quadrant II, ![]()
54. ![]()
55. ![]()
Show Solution
![]() Quadrant IV,
Quadrant IV, ![]()
For the following exercises, find the requested value.
56. If ![]() and
and ![]() is in the fourth quadrant, find
is in the fourth quadrant, find ![]()
57. If ![]() and
and ![]() is in the first quadrant, find
is in the first quadrant, find ![]()
Show Solution
![]()
58. If ![]() and
and ![]() is in the second quadrant, find
is in the second quadrant, find ![]()
59. If ![]() and
and ![]() is in the third quadrant, find
is in the third quadrant, find ![]()
Show Solution
![]()
60. Find the coordinates of the point on a circle with radius 15 corresponding to an angle of ![]()
61. Find the coordinates of the point on a circle with radius 20 corresponding to an angle of ![]()
Show Solution
![]()
62. Find the coordinates of the point on a circle with radius 8 corresponding to an angle of ![]()
63. Find the coordinates of the point on a circle with radius 16 corresponding to an angle of ![]()
Show Solution
![]()
64. State the domain of the sine and cosine functions.
65. State the range of the sine and cosine functions.
Show Solution
![]()
Graphical
For the following exercises, use the given point on the unit circle to find the value of the sine and cosine of ![]()
66. 
67. 
Show Solution
![]()
68. 
69. 
Show Solution
![]()
70. 
71. 
Show Solution
![]()
72. 
73. 
Show Solution
![]()
74. 
75. 
Show Solution
![]()
76. 
77. 
Show Solution
![]()
78. 
79. 
Show Solution
![]()
80. 
81. 
Show Solution
![]()
82. 
83. 
Show Solution
![]()
84. 
85. 
Show Solution
![]()
Technology
For the following exercises, use a graphing calculator to evaluate.
86. ![]()
87. ![]()
Show Solution
−0.1736
88. ![]()
89. ![]()
Show Solution
0.9511
90. ![]()
91. ![]()
Show Solution
−0.7071
92. ![]()
93. ![]()
Show Solution
−0.1392
94. ![]()
95. ![]()
Show Solution
−0.7660
Extensions
For the following exercises, evaluate.
96. ![]()
97. ![]()
Show Solution
![]()
98. ![]()
99. ![]()
Show Solution
![]()
100. ![]()
101. ![]()
Show Solution
![]()
102. ![]()
103. ![]()
Show Solution
![]()
104. ![]()
105. ![]()
Show Solution
0
Real-World Applications
For the following exercises, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point ![]() that is, on the due north position. Assume the carousel revolves counter clockwise.
that is, on the due north position. Assume the carousel revolves counter clockwise.
106. What are the coordinates of the child after 45 seconds?
107. What are the coordinates of the child after 90 seconds?
Show Solution
![]()
108. What are the coordinates of the child after 125 seconds?
109. When will the child have coordinates ![]() if the ride lasts 6 minutes? (There are multiple answers.)
if the ride lasts 6 minutes? (There are multiple answers.)
Show Solution
37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds
110. When will the child have coordinates ![]() if the ride lasts 6 minutes?
if the ride lasts 6 minutes?
Glossary
- cosine function
- the x-value of the point on a unit circle corresponding to a given angle
- Pythagorean Identity
- a corollary of the Pythagorean Theorem stating that the square of the cosine of a given angle plus the square of the sine of that angle equals 1
- sine function
- the y-value of the point on a unit circle corresponding to a given angle


